有轨电车荷载作用下路基应力响应分析

王浩然

(1.上海市城市建设设计研究总院(集团)有限公司,上海 200125; 2.同济大学地下建筑与工程系,上海 200092)

0 引 言

随着国民经济的迅猛发展,城市建设日新月异,随着国民生活水平的不断提高,私人汽车的保有量不断增加,然而随后由此引发了一系列环境问题,频频出现的雾霾天气,坚定了国家对大气污染坚决治理的决心。有轨电车具有高效、安静、环保等优点,近些年来越来越受到各地区的关注。我国现代有轨电车尚属起步阶段,缺乏相对应的规范来指导设计,目前只能参照普通铁路、地铁等相关规范。在已有的工程项目设计中,设计人员发现有轨电车荷载水平明显要低于传统地铁和铁路等交通动载,前者在运营期的运行速度要明显低于后者。因此,理论上有轨电车荷载作用于地基产生的动应力扩散效应与铁路路基相比将有显著的差异性。本文将采用三维显式动力有限元,对有轨电车应力响应特性及传播机理进行分析。

1 有轨电车基本参数

1.1 路基基床参数

有轨电车路基采用整体道床结构,其标准横断面如图1所示,基床中各结构层材料参数如表1所示。至于地基土材料参数,根据连续介质理论,地基土采用弹性材料不会给应力计算带来太大的误差。上海第③层土的压缩模量为2.2～5.9 MPa[1],取平均值4 MPa。有限元程序中需要输入的土层模量是弹性模量,弹性模量可取压缩模量的6.5倍[2]。

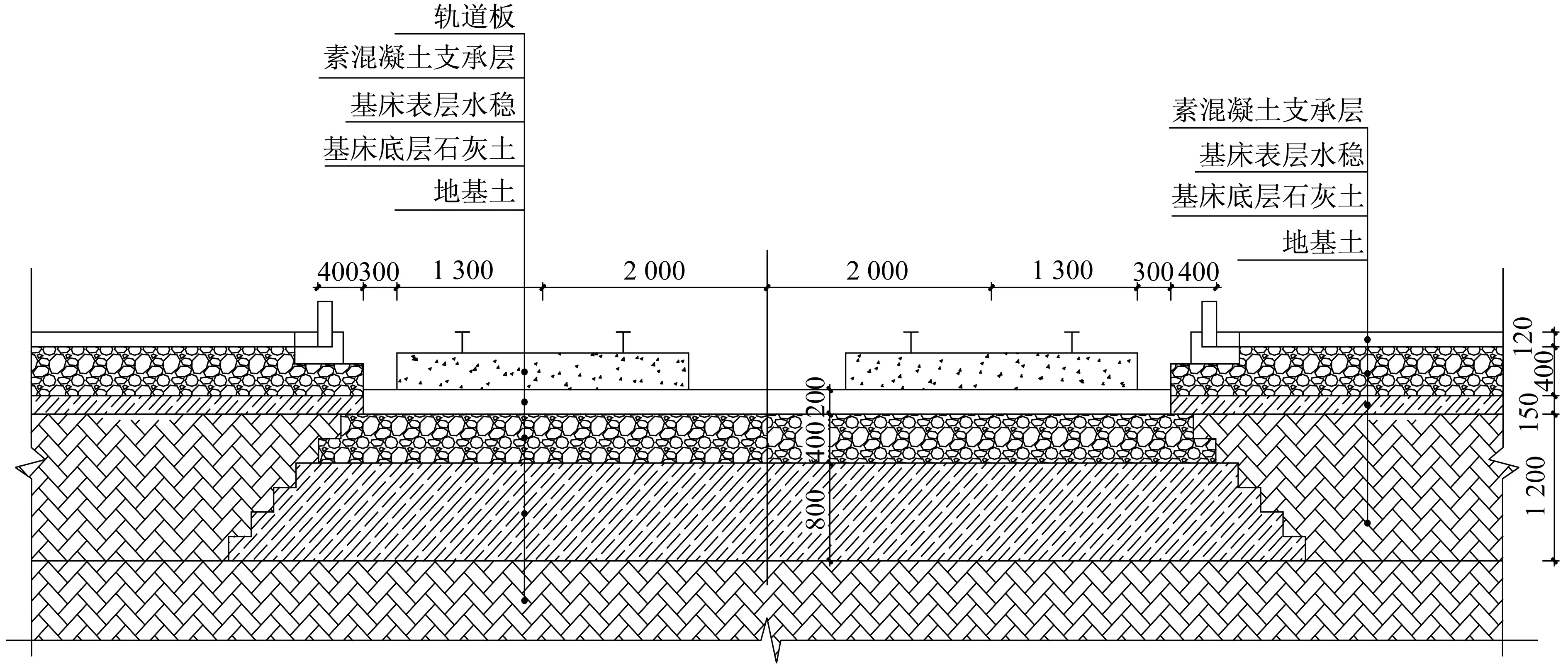
图1 有轨电车路基标准横断面(单位:mm)Fig.1 Subgrade standard cross section of tramcar (Unit:mm)

表1基床材料参数

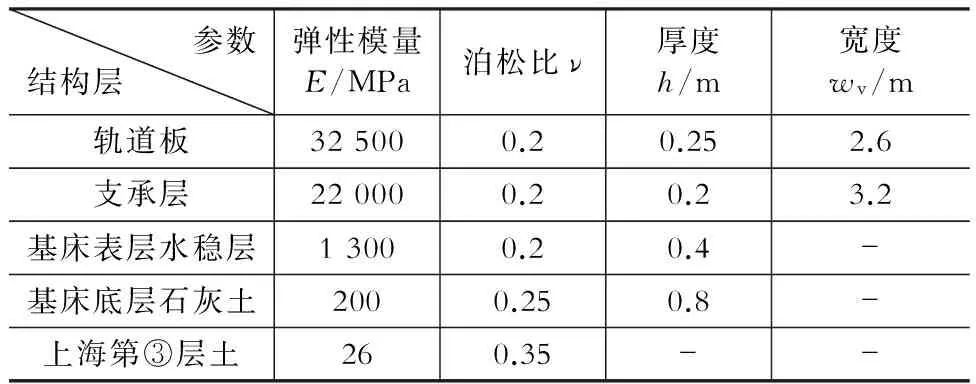
Table 1 Material parameters of subgrade bed

1.2 车辆及轨道参数

有轨电车车辆轴距1.7 m,定距11.1 m,满载轴重12.5 t,设计速度70 km/h。轨道板上下行分开,单块轨道板宽2.6 m、长12.5 m、厚0.25 m,采用C40钢筋混凝土板,轨道扣件间距0.6 m,车辆模型如图2所示。

2 模型建立

2.1 荷载施加

对于整体道床可认为轮轨荷载由5个弹性扣件承担,分担比为0.1,0.2,0.4,0.2,0.1,并经弹性扣件传递至轨道板,当考虑临近轮轴的影响时,如图3所示,纵向分布总长度4.1 m。荷载横向分布范围等于轨道板宽度2.6 m。

轮轨荷载可以以半正弦波脉冲表示[3],如公式(1)所示。

p(t)=Psin2(2πft)

(1)

式中,p(t)为轮载;P为轮载峰值;f为荷载作用频率。

轮载峰值P可以根据经验公式计算[4],如公式(2)所示。

P=P静(1+0.003v)

(2)

式中,P为轮载峰值;P静为静轮载;v为速度,km/s。

荷载作用频率f可以根据车辆定距11.1 m及行车速度v求得,不同行车速度所对应的荷载频率如表2所示。

表2荷载频率

Table 2 Loading frequency

整体道床结构假设路基面荷载均匀分布,如图4所示,因此每对轮轴下的轨道板竖向荷载为

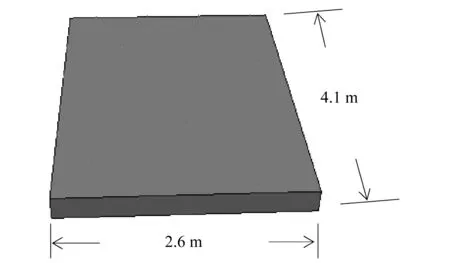
图4 荷载分布Fig.4 Load distribution

以上所述的有轨电车移动半正弦波荷载可以通过VDLOAD用户子程序的二次开发实现。

2.2 建模

1) 人工边界选取

采用有限元模拟静力问题时,只需要保证边界与所关心的区域足够远即可忽略边界效应对结果的影响。但是进行动力问题模拟时,应力波会在边界处发生虚拟反射,为了避免应力波反射,需要设置人工边界条件。ABAQUS 显式分析模块基于Zienkiewicz[5]的无限元理论及Lysmer[6]的黏性理论创立了无限元人工边界。在建模中,无限元的节点排列是有特定要求的,它必须按照逆时针的规律进行排序,而且单元的第一个面要求是有限元和无限元的交界面,如图5所示。无限元的延伸反向不能交叉,图6给出了正确和错误的无限元示例[7]。

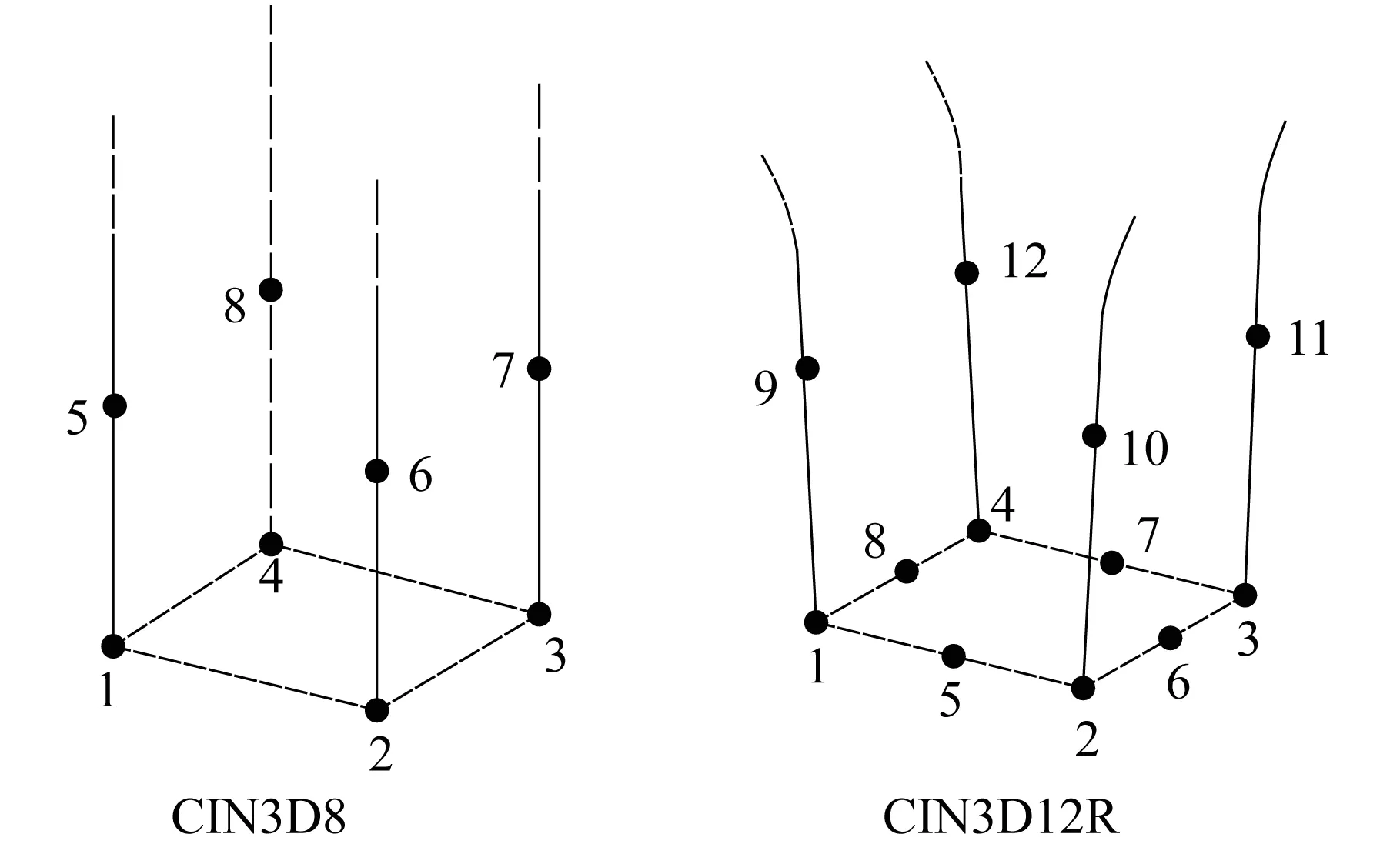
图5 无限元节点编号规则Fig.5 Arrangement rules of infinite element nodes

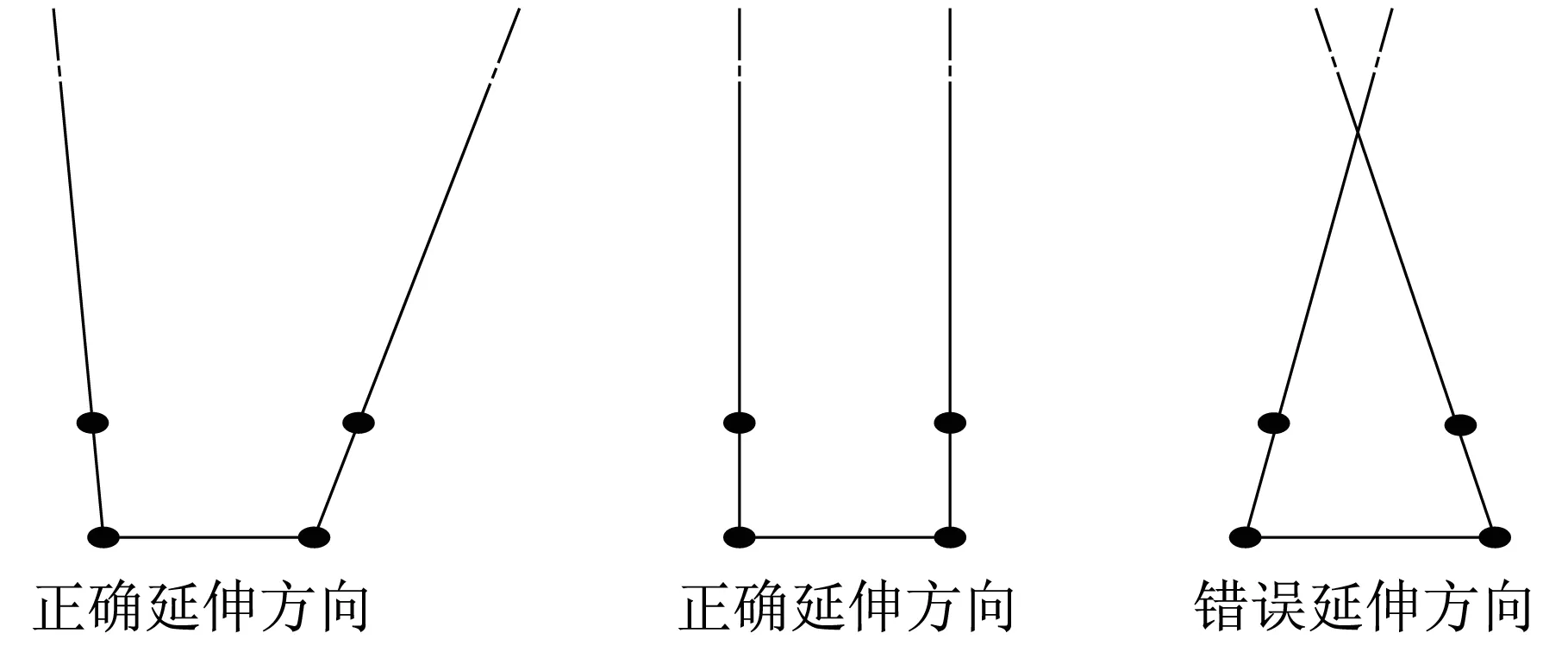
图6 无限元延伸方向Fig.6 Extending direction of infinite element

2) 模型几何形状

要保证对边界处的应力波具有良好吸收效果,一方面需要选取合适的人工边界,另一方面需要建立合适的几何模型。当应力波以不同的入射角入射到人工边界时,人工边界吸收效果会有差异[8]。Connolly建立了拉长的球形模型[9],使得移动荷载激起的应力波能最大限度地以较优入射角的方式进入边界,从而提高了人工边界的吸收效果。

直接在Abaqus建立拉长半球形模型时,边界处无限元单元节点号无法按程序所要求的顺序进行排列,对此本文采用Matlab软件编制无限元节点生成程序,使得模型节点能按Abaqus软件的要求进行排列。综合以上所述,可以建立有限元模型及相应网格分别如图7和图8所示。

3 计算结果

3.1 正常运营速度下路基应力响应

有轨电车的最高运行速度是70 km/h,一般来说,实际的运行速度会保持在25 km/h左右。由图9、图10可知,荷载经过引起的附加竖向应力σz随深度增加,其幅值迅速衰减,在深度0.7 m的位置,附加应力衰减了50%。对于荷载驶近与驶离时,荷载移动带下方各点经受了3次半正弦波荷载的激振,因此在进行路基铺筑时,需要更加注意上中垫层的压实质量,并提高其疲劳强度。根据相应《上海市建筑地基基础设计》中软土地基中附加应力占自重应力的10% 的判断标准,可求得动应力影响深度约2.9 m。

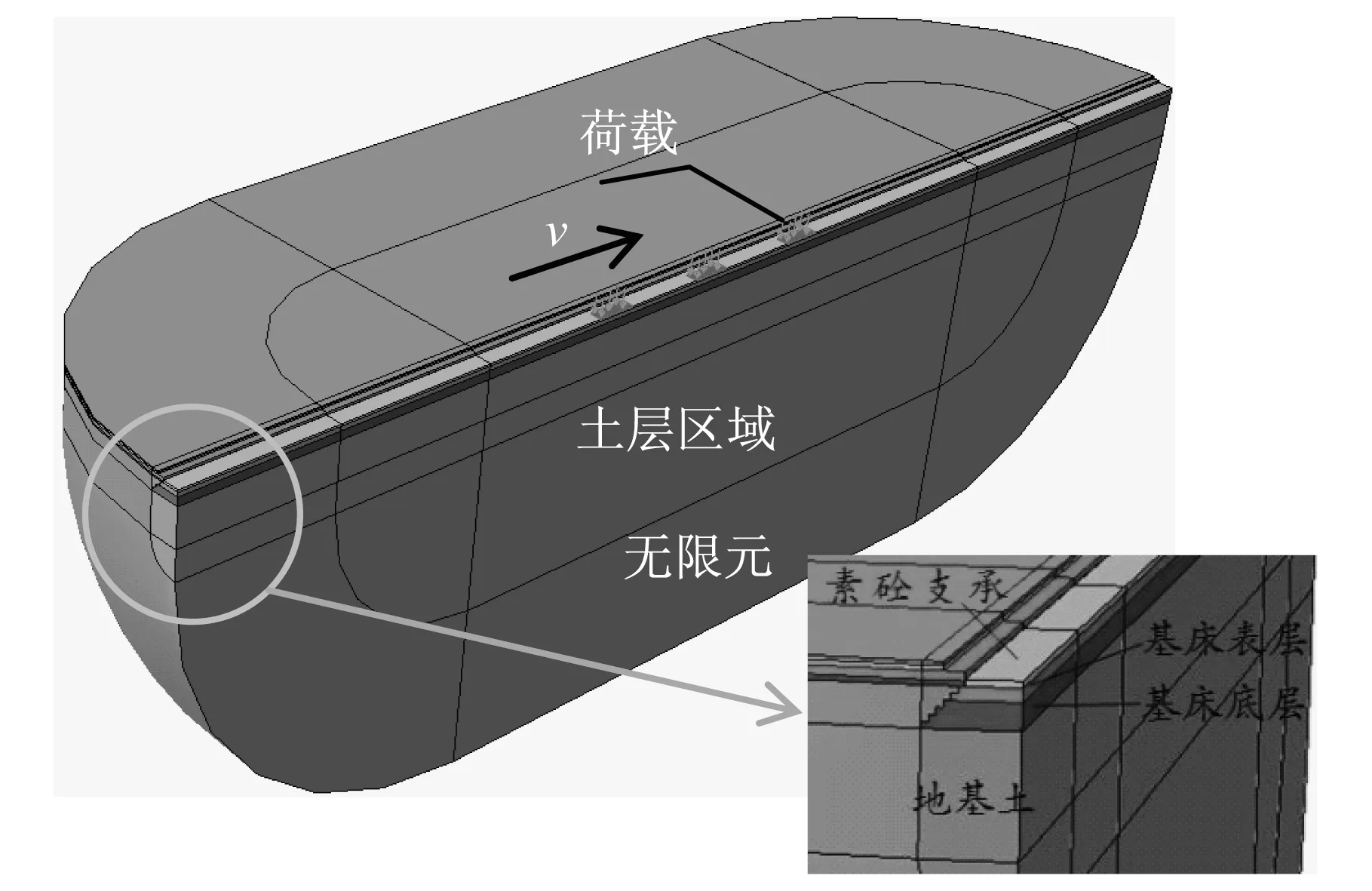
图7 三维有限元模型Fig.7 Three-dimensional finite element model

图8 网格划分Fig.8 Finite element mesh

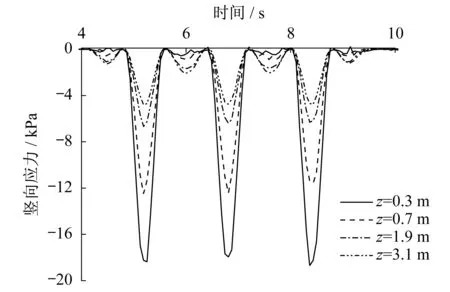
图9 竖向应力σz随时间变化规律Fig.9 Vertical stress σz vs time

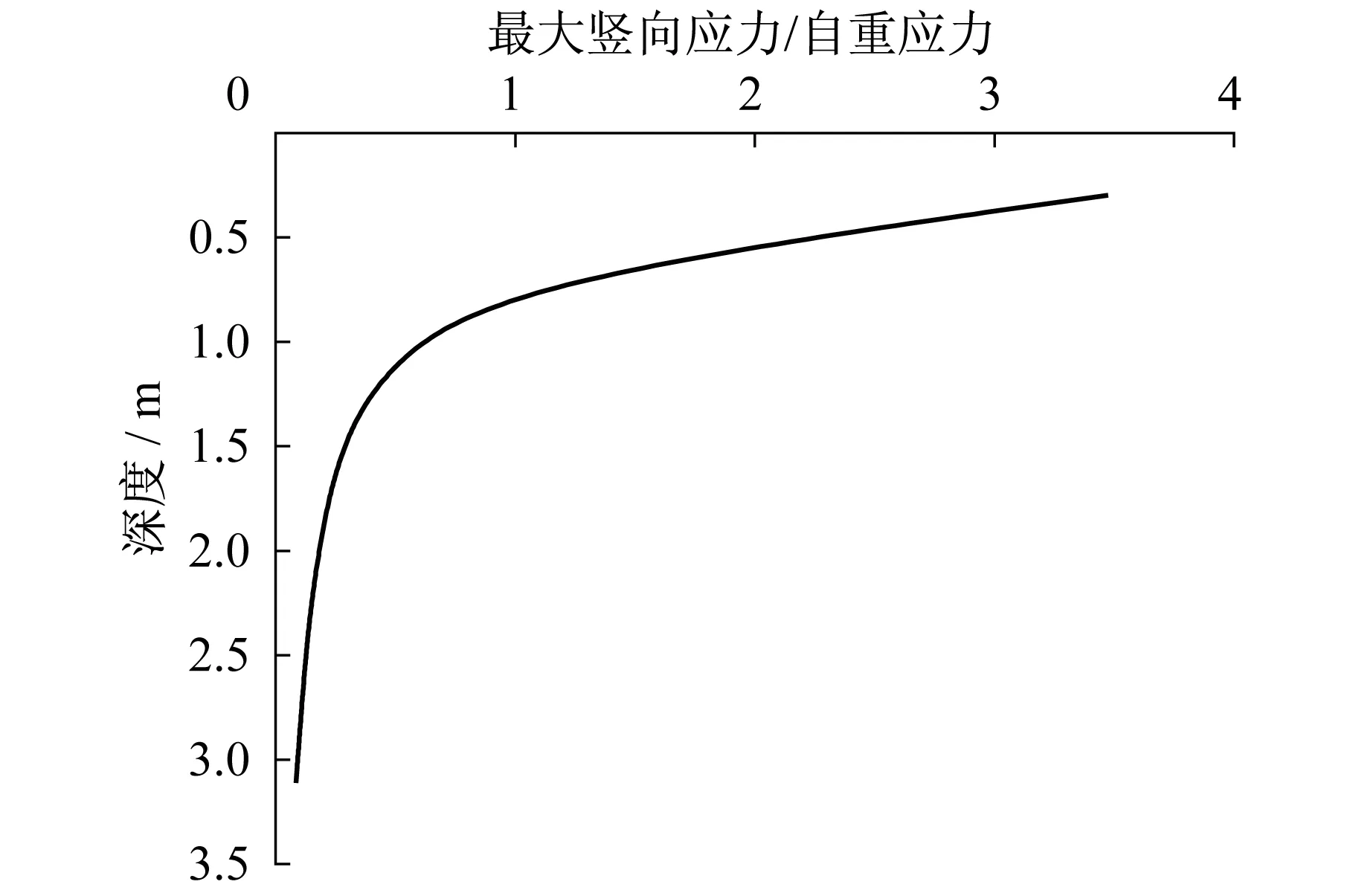
图10 最大竖向应力随深度变化规律Fig.10 The maximum vertical stress vs depth

3.2 运营速度对路基应力响应的影响

考虑到有轨电车不会一直以恒定速度运行,不同路段或运营工况下,其运营速度会发生变化,最高运营速度可达到70 km/h。本节将对速度与应力响应之间的关系进行分析。由图11可知,不同速度下竖向附加应力随深度的衰减规律基本相同,随着速度的增加,应力的影响深度不断加大,以软土地基中附加应力等于自重应力10%的标准判断,运营速度从10 km/h到70 km/h变化时,应力影响深度从2.8 m增加到3.2 m。有轨电车以最大运营速度为70 km/h,此速度下应力影响深度达到3.2 m,地基沉降计算深度或地基处理设计深度可以参照此深度进行。

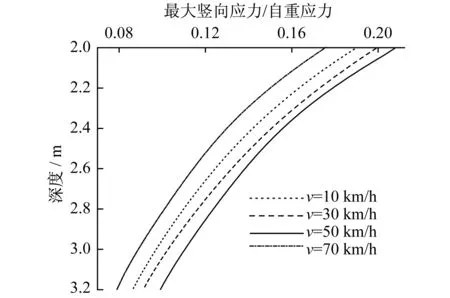
图11 不同速度下最大竖向应力随深度变化规律Fig.11 The maximum vertical stress vs depth at different speed

4 结 论

(1) 荷载经过引起的附加竖向应力σz随深度增加,其幅值迅速衰减,在深度0.7 m的位置,附加应力衰减了50%。每运行一次路基下方个点都经受了3次半正弦波荷载的激振,因此要提高上中垫层的压实质量保证抗疲劳强度。以附加应力占自重应力的10% 的标准,该速度下动应力影响深度约2.9 m。

(2) 附加动应力峰值及影响深度与运营速度存在正相关的关系,当有轨电车达到最大运营速度70 km/h时,动应力影响深度为3.2 m,该值可作为路基沉降计算深度及地基处理深度的参考值。

[1] 37-2012 D G J.上海市岩土工程勘察规范 [S]].出版社,2002.

37-2012 D G J.Code for investigation of geotechnical engineering[S].Location,Press,2012.(in Chinese)

[2] 中国振动工程学会土动力学专业委员会.土动力学工程应用实例与分析[M].北京:中国建筑工业出版社,1998:193-200.

Special Committee of Soil Dynamics,Chinese Society for Vibration Engineering.Applications and analyses of soil dynamics in engineering[M].Beijing:China Architecture & Building Press,1998:193-200.(in Chinese)

[3] 薛富春,张建民.移动荷载作用下高速铁路轨道-路基-地基耦合系统振动加速度的空间分布特征[J].岩土工程学报,2014,12:2179-2187.

Xue Fuchun,Zhang Jianmin.Spatial distribution of vibration accelerations in coupled rail-embankment foundation system on high-speed railway under moving loads[J].Chinese Journal of Geotechnical Engineering,2014,36(12):2179-2187.(in Chinese)

[4] 屈晓辉,崔俊杰.客运专线铁路路基设计技术[M].北京:人民交通出版社,2008.

Qu Xioahui,Cui Junjie.Design technology of railway subgrade for passenger dedicated line[M].Beijing:China Communications Press,2008.(in Chinese)

[5] Zienkiewicz O C,Emson C,Bettess P.A novel boundary infinite element[J].International Journal for Numerical Methods in Engineering,1983,19(3):393-404.

[6] Lysmer J.Finite dynamic model for infinite media[C]Proc.of ASCE,1969:859-877.

[7] 费康,张建伟.ABAQUS 在岩土工程中的应用[M].北京:中国水利水电出版社,2010.

Fei Kang,Zhang Jianwei.Application of ABAQUS in geotechnical engineering [M].Beijing:China Water Power Press,2010.(in Chinese)

[8] Kouroussis G,Van Parys L,Conti C,et al.Using three-dimensional finite element analysis in time domain to model railway-induced ground vibrations[J].Advances in Engineering Software,2014,70:63-76.

[9] Connolly D,Giannopoulos A,Forde M C.Numerical modelling of ground borne vibrations from high speed rail lines on embankments[J].Soil Dynamics and Earthquake Engineering,2013,46:13-19.