钢-混组合连续梁不同有限元模拟差异性分析

党 岩 吴用贤 李方元

(1.同济大学建筑设计研究院(集团)有限公司,上海 200092; 2.同济大学桥梁工程系,上海 200092)

0 引 言

钢-混组合梁是指将钢梁与混凝土桥面板通过抗剪连接件连接成整体并考虑共同受力的桥梁结构。组合梁最大的技术特点是组合后的性能已经超过两种材料各自的力学性能,兼有钢材和混凝土的优点同时又具有良好的力学性能和施工性能,加上造价相对低廉,桥型轻盈美观,近年来国内外的工程应用和相关研究越来越多,在桥梁结构领域显现出了广阔的应用前景[1-2]。然而由于组合梁是由两种完全不同的材料组合而成,因此正确模拟两种材料之间的连接就成为了关键。本文以绍兴市某新建工程为例,分别采用梁单元和板单元模拟桥面板,按四种不同模拟方法进行了对比,在此基础上进一步对组合梁结构进行了分析和研究。

1 工程结构概况

该桥位于绍兴市斗门镇,纵向布置30 m+30.39 m+30 m,桥梁横断面见图1,桥面全宽8 m,包括0.3 m防撞护栏+7.4 m行车道+0.3 m防撞护栏。全桥采用等高结构,高1.62 m,其中主梁高1.3 m。钢梁为I字形截面,为增加截面整体性,钢梁每隔5 m设1道I字形横梁。

混凝土桥面板横向跨中厚22 cm,主梁位置渐变至32 cm;悬臂长1.75 m,主梁处至悬臂端桥面板厚度渐变至18 cm,具体构造如图1所示。

图1 标准横断面(单位:mm)Fig.1 The standard cross-section (Unit:mm)

2 力学模型

2.1 计算参数

(1) 一期恒载:主梁顶、底和腹板采用实际板厚,钢材考虑各种加劲肋后,重力密度取89.4 kN/m3;混凝土桥面板考虑钢筋后,重力密度取26 kN/m3。

(2) 二期恒载:桥面铺装为1.2 kN/m2;两侧防撞栏杆各取10 kN/m。

(3) 移动荷载:考虑此桥修建在老桥下部基础上,汽车荷载采用老桥标准汽车-15级;人群荷载考虑满布情况。

(4) 均匀温度:考虑整体升、降温30 ℃。

(5) 梯度温度:参照JTG D60通用规范规定,升温取T1=20 ℃,T2=6.7 ℃,降温效应按一半考虑[3]。

(6) 支座不均匀沉降:由于本桥是拆除旧桥上部结构,在旧桥下部基础上建新桥,因此认为支座沉降已经完成,模型中不考虑该项作用。

(7) 混凝土收缩徐变:考虑1 000天。

2.2 计算模型

目前,对于组合梁的模拟基本上使用以下几种方法:一种是主梁和桥面板采用同一个单元,使用Midas Civil的联合截面功能或“桥梁博士”软件的附加截面功能[4];另一种是主梁和桥面板均采用梁单元模拟,梁板间采用刚臂连接[5];或者主梁采用梁单元而桥面板采用板单元模拟,两者之间通过设置截面偏心共节点或者采用刚臂连接[6]。

本文分别采用“桥梁博士”和Midas Civil分别以以下四种模型进行计算,并对主要计算结果作比较,见表1。

3 结果对比与分析

为了全面对比上述四种模型模拟方法的精度与差异性,结合此工程,对整个施工阶段进行了详细地模拟,对比各项结果并给予分析:

(1) 施工各阶段混凝土桥面板和主梁在边跨跨中和中支点各自上下缘的应力。

(2) 使用阶段结构竖向位移。

(3) 成桥阶段考虑1 000天的混凝土收缩徐变下混凝桥面板的应力状况。

(4) 对于钢混组合连续梁,通过施工过程中对中支点的预顶,给予中支点附近桥面板一定的预压力,以防止正常使用过程中支点附近桥面板拉应力过大而开裂[1]。因此考虑了不同的顶升量产生的预压效果,并在正常使用极限状态下计算了裂缝宽度[7-8]。

表1四种模拟方法

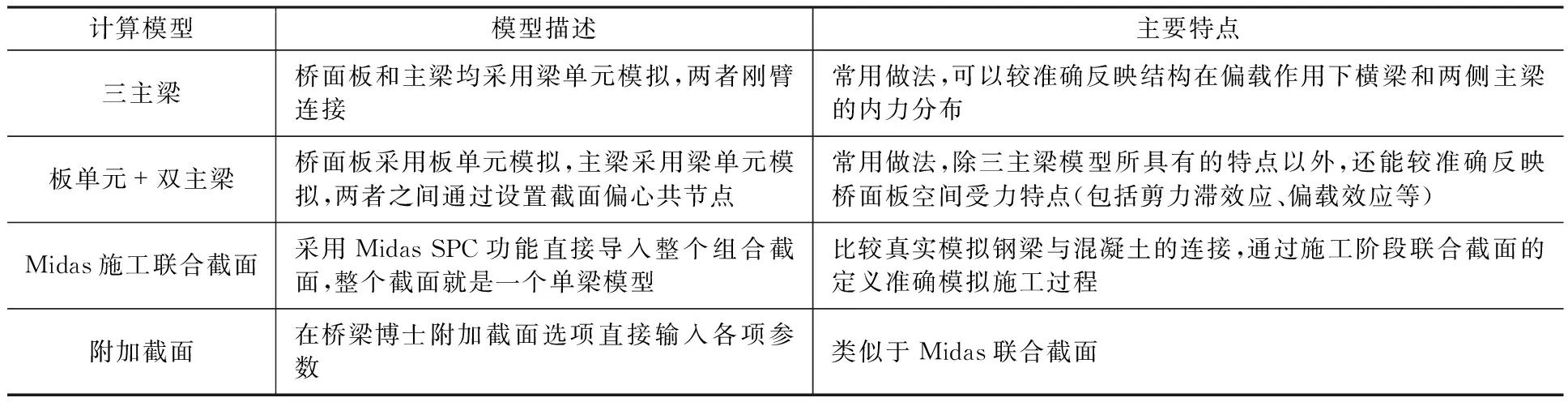
Table 1 Four simulation methods

(5) 根据模型提取出来的组合梁整体内力和各部分内力验证软件的可靠性。

3.1 各施工阶段结构不同位置的应力状况

本桥施工分以下7个施工阶段:

(1) CS1:钢结构主梁整体吊装就位。

(2) CS2:预制混凝土桥面板安装就位。

(3) CS3:中支点附近以外的桥面板湿接缝浇筑。

(4) CS4:千斤顶对中支点进行顶升150 mm。

(5) CS5:中支点附近桥面板湿接缝浇筑。

(6) CS6:千斤顶回落,解除预顶。

(7) CS7:二期铺装施工。

由于本桥边中跨比为1∶1,边跨的作用效应较中跨显著,因此以边跨跨中结果作为主要分析依据。

四种不同模型边跨跨中在各施工阶段的应力变化情况,通过对比可以得到各个模型在施工阶段模拟的差异性并不十分明显,具体情况如图2-图5所示。图中结果以压应力为正,拉应力为负。

图2 边跨跨中桥面板应力Fig.2 The stress of bridge deck at the side span

图3 中支点桥面板应力Fig.3 The stress of bridge deck in the central bearing point

图4 边跨跨中钢主梁应力(MPa)Fig.4 The stress of steel beam at the side span (MPa)

同时根据主梁剪力钉布置情况和《公路钢混组合桥梁设计与施工规范》(JTG/T D64)[8]计算发现,该桥全长范围内混凝土桥面板全宽有效,剪力滞效应可以忽略,因此板+双主梁模型中桥面板应力取板单元中心线处值。

从模拟整个结构的施工过程来看,四种模型对应的模拟结果可以认为是一致的,相互之间差值并不是很明显。

图5 中支点钢主梁应力Fig.5 The stress of steel beam in the central bearing point

通过仔细对比各个模型在各施工阶段桥面板和主梁上下缘应力发现:

(1) 对于桥面板上缘应力,在桥面板和主梁没有形成整体受力之前,四种模型结果基本一致,虽然相互之间稍有波动,但并无多大差异;在两者形成整体后共同承担外荷载的作用下,在CS6和CS7两个施工阶段,四种模型结果出现了稍微明显的差异,以边跨跨中桥面板为例,板+双主梁模型中桥面板拉应力最大(1.6 MPa),三主梁模型次之(1.4 MPa),联合截面和附加截面模型结果较一致,分别为1.3 MPa和1.2 MPa,对于偏于保守的设计而言,可将板+双主梁模型计算结果作为设计参考。

(2) 对于桥面板下缘应力,上述现象则表现得更加明显。

(3) 对于钢主梁上下缘应力,四种模型可以认为基本没有差别,差别最大的板+双主梁模型最大相对误差不超过6%。

3.2 正常使用阶段结构位移

根据《公路桥涵设计通用规范》(JTG D60—2004)[3]4.1.6规定计算,结构在正常使用极限状态短期最不利组合作用下,四个模型在中跨跨中和边跨跨中的位移也比较接近,相互之间最大相对误差不超过5.3%。具体数值见表2。

表2正常使用极限状态下结构位移

Table 2 Structure diaplacement in the serviceability limit state

综上可以认为,上述出现的差异是由于桥面板和主梁之间连接的模拟方法不同所造成的,对于通过节点之间刚臂连接桥面板和主梁的三主梁模型和板+双主梁模型,这种误差是不可避免的,但是对于整体结构的纵向分析,作者认为其结果是可信的,同时联合截面和附加截面模型更加准确地模拟了这种连接,其结果可以说可信度更高。但四种模型其实各有利弊,有时可能需要在整体结构分析中提取结构偏载效应引起的多根主梁内力分布情况、横梁受力情况、桥面板剪力滞效应等,这种情况下三主梁模型和板+双主梁模型的结果可以提供较为准确的参考[9];如果仅仅需要结构纵向整体受力情况,单梁模型(联合截面模型和附加截面模型)则完全可以满足要求。

3.3 收缩徐变引起的桥面板应力情况

混凝土收缩徐变特有的效应对混凝土结构的影响长期受到关注,尤其是近年来组合结构桥梁的发展,混凝土收缩徐变效应对组合梁受力性能的影响引起了广泛关注。对于组合连续梁,在中支点负弯矩区域,收缩徐变可能 混凝土裂缝提前出现或加速裂缝的扩展,从而导致梁体整体刚度下降,以至降低结构的受力性能[10]。因此有必要计算和分析组合连续梁的长期受力性能。

本文在成桥阶段考虑1 000天混凝土收缩徐变引起的桥面板拉应力状况如图6-图13所示,部分具体数值见表3。

图6 板+双主梁模型徐变引起的桥面板上缘应力(单位:MPa)Fig.6 The upper edge stress of deck induced by creep in the plate and double girders model (Unit:MPa)

图7 三主梁模型徐变引起的桥面板上缘应力(单位:MPa)Fig.7 The upper edge stress of deck induced by creep in the three girders model (Unit:MPa)

图8 联合截面模型徐变引起的桥面板上缘应力(单位:MPa)Fig.8 The upper edge stress of deck induced by creep in the union section model (Unit:MPa)

图9 附加截面模型徐变引起的桥面板上缘应力(单位:MPa)Fig.9 The upper edge stress of deck induced by creep in the additional section model (Unit:MPa)

图10 板+双主梁模型收缩引起的桥面板上缘应力(单位:MPa)Fig.10 The upper edge stress of deck induced by shrinkage in the plate and double girders model (Unit:MPa)

图11 三主梁模型收缩引起的桥面板上缘应力(单位:MPa)Fig.11 The upper edge stress of deck induced by shrinkage in the three girders model (Unit:MPa)

图12 联合截面模型收缩引起的桥面板上缘应力(单位:MPa)Fig.12 The upper edge stress of deck induced by shrinkage in the union section model (Unit:MPa)

图13 附加截面模型收缩引起的桥面板上缘应力(单位:MPa)Fig.13 The upper edge stress of deck induced by shrinkage in the additional section model (Unit:MPa)

表3收缩徐变下各模型中桥面板上缘拉应力

Table 3 The upper edge stress of deck induced by creep and shrinkage in the different models MPa

从结果可看出,三主梁模型和联合截面模型的结果非常接近,板+双主梁模型中徐变和收缩产生的应力较大,“桥梁博士”软件附加截面模型中徐变产生的应力较大,收缩产生的应力较小。其中,板+双主梁模型在徐变作用下产生的应力提取了两个值,括号内为剔除应力集中后的真实值。

通过调用软件内部混凝土收缩徐变计算器,发现对于混凝土收缩应变终极值和徐变系数的计算结果,三主梁模型和联合截面模型与《公路钢筋混凝土及预应力混凝土桥涵设计规范》[7]表6.2.7较吻合,而板+双主梁模型和附加截面模型的计算结果则有一定偏差。

结合目前规范规定的混凝土收缩徐变的计算方法[7-8],其主要是针对单向应力状态进行计算分析,若将计算单向应力状态的徐变、收缩理论应用于多向应力状态的板单元,必然会产生误差,而关于计算板单元的徐变系数和收缩应变到目前为止还是一个有待研究的问题[11]。

而关于“桥梁博士”计算混凝土桥面板收缩徐变结果[12]理论上应和Midas Civil结果一致,之所以出现偏差,仔细分析是因为本次“桥梁博士”附加截面模型为了方便起见,只取了标准横断面的一半进行建模,程序在自动识别截面和提取截面数据时,构件理论厚度h的自动计算与实际并不相符,产生了一定误差,其值并不可信[7],如果采用全结构模型,在构件理论厚度计算正确的情况下,结果是可以预测的[12]。

3.4 负弯矩区性能改善方法对比情况

以Midas施工联合截面模型为例,针对施工过程中中支点处钢梁不同顶升量(h)和桥面板不同钢筋用量(As)对桥面板负弯矩区性能的改善情况为研究对象,以正常使用阶段裂缝宽度(Wtk)的验算[7-8,13]为衡量标准进行了探讨。

其中,对于桥面板不同钢筋用量分别考虑了钢筋间距ds为150 mm,120 mm和100 mm三种情况,其分别对应的钢筋用量为31 396 mm2,39 245 mm2和47 094 mm2,具体对比结果见图14和表4。

图14 不同顶升量下桥面板裂缝宽度Fig.14 The crack width of deck in different lifting amounts

表4不同顶升量下中支点处桥面板裂缝宽度

Table 4 The crack width of deck in the central bearing point in different lifting amounts

注:As表示桥面板钢筋用量,Wtk表示中支点处桥面板裂缝宽度,h表示中支点处钢梁顶升量

可以看出,在桥面板钢筋用量相同的情况下,中支点处桥面板裂缝宽度与顶升量呈线性关系,而且随着顶升量增加裂缝宽度逐渐减小;对于桥面板钢筋用量的问题,可根据实际施工情况结合适当的顶升量选用钢筋间距。

因此在施工过程中,结合中支点处钢梁顶升和桥面板合适的钢筋用量两种方法能够有效控制桥面板负弯矩区裂缝宽度,较好地满足规范对钢筋混凝土桥面板最大裂缝宽度的要求,极大地改善了组合梁内力,加强了混凝土板和钢梁的结合。

3.5 模型提取内力的对比与验证

针对模型提取的正常使用极限状态下短期最不利组合组合梁整体弯矩和混凝土桥面板的轴力,通过和组合梁在荷载作用下依据截面分力法[1]计算得出的结果进行对比,验证模型的可靠性,具体对比结果见表5。

表5模型提取内力对比

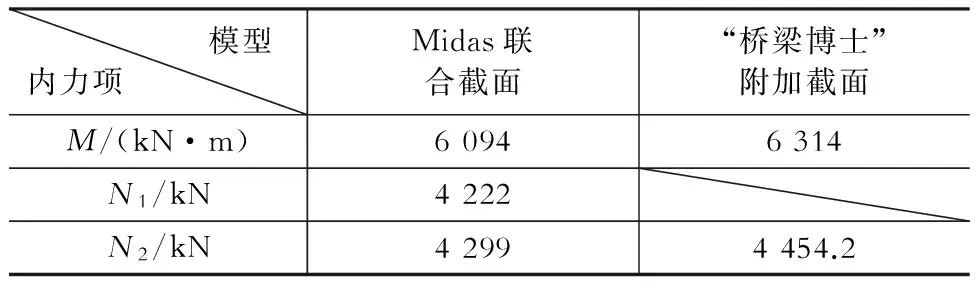
Table 5 Comparison of internal force in different models

注:M表示模型提取的截面整体弯矩,N1表示模型提取的混凝土桥面板轴力,N2表示依据截面分力法由M计算得到的混凝土桥面板分配到的轴力

可以看到,Midas联合截面模型提取出来的混凝土桥面板轴力与通过截面分力法[1]计算得到桥面板分配到的轴力相比,相对误差为1.82%,可以认为模型结果是一致的;“桥梁博士”附加截面模型由于软件本身所限制,无法提取混凝土桥面板自身轴力,因此我们对于其提取出来的截面整体弯矩及根据截面分力法[1]计算得到的桥面板轴力和Midas联合截面模型作对比,可以看到,它们之间相对误差为3.61%,基于前一方法的误差相比较,也可以认为是可靠的。

4 结 论

(1) 对于钢-混凝土组合梁的施工过程分析,上述四种模拟方法均可满足实际工程精度要求,计算结果没有明显区别。

(2) 传统模拟组合梁的方法在桥面板和钢梁相对应的节点处加刚臂,保证两者之间无相对滑移,内力图、应力图呈锯齿状;联合截面和附加截面相当于在纵向施加了均匀刚臂,内力图、应力图过度较连续。

(3) 四种分析模型中,板+双主梁和三主梁模型,可以初步提供结构的部分空间效应(如剪力滞、偏载、横梁受力情况等),供设计人员参考;联合截面和附加截面模型大同小异,从纵向整体计算来看比前两种模型在建模、查看结果方面都更加方便。

(4) 以改善钢混组合连续梁负弯矩区性能为例,从本次三跨连续梁的分析结果可以看出,选取合适的钢梁起顶量和桥面板钢筋用量,对于改善混凝土桥面板负弯矩区裂缝宽度效果显著。

(5) 根据模型提取的内力结果和组合梁本身截面分力法理论做对比,Midas联合截面和“桥梁博士”附加截面的结果都是非常可靠的。

[1] 刘玉擎.组合结构桥梁[M].北京:人民交通出版社,2005.

Liu Yuqing.Steel-concrete composite bridge[M].Beijing;China Communications Press,2005.(in Chinese)

[2] 聂建国,陶慕轩,吴丽丽,等.钢-混凝土组合结构桥梁研究新进展[J].土木工程学报,2012(6):110-122.

Nie Jianguo,Tao Muxuan,Wu Lili,et al.Advances of research on steel-concrete composite bridges[J].China Civil Engineering Journal,2016(6):110-122.(in Chinese)

[3] 中华人民共和国交通部 JTG D60—2004,公路桥涵设计通用规范[S].北京:人民交通出版社,2004.

Ministry of Communications of the PRC.JTG D60—2004 General code for design of highway bridges and culverts[S].Beijing:China Communications Press,2004.(in Chinese)

[4] 周祥树,吴建东.简支钢-混叠合梁桥上部结构设计分析[J].市政技术,2012(6):46-48.

Zhou Xiangshu,Wu Jiandong.Superstructure design analysis of simple supported steel-concrete composite bridge[J].Municipal Engineering Technology,2012(6):46-48.(in Chinese)

[5] 程俊瑞,李瑞.钢-混叠合梁在旧桥改造设计中的应用[J].公路,2014(7):241-244.

Cheng Junrui,Li Rui.Application of steel-concrete composite beams in the reconstruction design of old bridges[J].Highway,2014(7):241-244.(in Chinese)

[6] 刘军,张哲,李文斌.钢-混叠合梁有限元分析[J].山东交通学院学报,2009(17):36-48.

Liu Jun,Zhang Zhe,Li Wenbin.Finite element analysis of steel-concrete composite bridges[J].Journal of Shandong Jiaotong University,2009(17):36-48.(in Chinese)

[7] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.

Ministry of Communications of the PRC.JTG D62—2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].BeiJing:China Communications Press,2004.(in Chinese)

[8] 中华人民共和国交通运输部.JTG/T D64—01—2015,公路钢混组合桥梁设计与施工规范[S].北京:人民交通出版社,2015.

Ministry of Communications of the PRC.JTG/T D64—01—2015,Specifications for design and construction of highway steel-concrete composite bridge[S].Beijing:China Communications Press,2015.(in Chinese)

[9] 李瑞琪,袁万城,高康,等.装配式简支钢-混组合小箱梁桥荷载横向分布系数的研究[J].结构工程师,2015(8):54-59.

Li Ruiqi,Yuan Wancheng,Gao Kang,et al.The analysis of the transverse distribution coefficient of the simply supported fabricated steel-concrete composite girder bridge[J].Structural Engineers,2015(8):54-59.(in Chinese)

[10] 苏庆田,戴昌源,许园春.分离式双箱组合梁斜拉桥收缩徐变效应分析[J].结构工程师,2015(6):56-62.

Su Qingtian,Dai Changyuan,Xu Yuanchun.Analysis of creep and shrinkage effects on separate twin-box composite girder of cable-stayed bridge[J].Structural Engineers,2015(6):56-62.(in Chinese)

[11] 荆国强.混凝土板单元在简单荷载下徐变收缩有限元计算方法的研究[D].上海:同济大学,2006.

Jing Guoqiang.Research on finite element calculation method of creep and shrinkage for concrete slab element under simple loads[D].Shanghai:Tongji University,2006.(in Chinese)

[12] 何飞.现行公路规范收缩应变、徐变系数与“桥梁博士”的比较[J].中国勘察设计,2010(5):47-49.

He Fei.Comparisons of shrinkage strain and creep coefficent between the existing highway code and doctorbridge software[J].Investigation & Design,2010(5):47-49.(in Chinese)

[13] 叶见曙.结构设计原理[M].北京:人民交通给出版社,2005.

Ye Jianshu.Principles of structure design[M].Beijing:China Communications Press,2005.(in Chinese)