Π形主梁斜拉桥中斜拉索索力传递机理研究

苗 林 金仁兴 陈德伟 蔡忠明

(1.上海建工集团股份有限公司,上海 200062; 2.同济大学桥梁工程系,上海 200092)

1 概 述

混凝土斜拉桥跨度不断增大的同时也从稀索体系向密索体系发展。由于斜拉索的加劲作用,密索体系斜拉桥的主梁已由受弯为主转变为受压弯为主的构件,截面形式也多采用带边肋的梁板结构。双边主肋梁截面(Π形梁)的推广更能有效地简化主梁结构,受力更加明确,更便于悬臂浇筑施工。

为满足日益增大的交通需求,行车道越来越多,使得公路桥梁肋板结构中两边肋间距变得较大,拉索锚固于两边肋上,索力通过边肋传至主梁全截面,引起桥面板应力的不均匀分布。

针对压弯荷载作用下,肋板截面应力分布或有效分布宽度模式的研究,较多采用的思路是从剪力滞后效应理论研究,到规范有效分布宽度的定义,再应用到实际设计中。其中,理论研究方法主要采用解析理论[1-2]、数值解法[3-7]、模型试验[8-11]等。综合上述研究表明,斜拉索索力的轴向分力对主梁纵向应力分布起主要影响作用;由于混凝土的徐变作用,纵向应力的不均匀程度在成桥后将逐渐减小,而施工期间的应力分布更加复杂,且分布曲线很难用单个参数进行描述。

在实际设计施工中,主梁的强度计算通常采用将弯矩乘以增大系数或实际截面按有效宽度加以折减[12],但我国现行规范[13]尚未对类似斜拉桥主梁的压弯构件有明确的规定。文献[14-15]建议斜拉索的计取滞后几个阶段,或者考虑轴向力按某一角度的扩散至整个横截面[10,16-17]。

本文利用最小势能原理,建立了肋板结构在压弯荷载作用下考虑率剪力滞后效应的微分方程,通过解析解分析斜拉索索力的传递规律;依托在建的上海市辰塔公路越黄浦江大桥,采用实体有限元模型,模拟整个悬臂施工过程,获得主梁有效宽度分布模式及索力传递机理;综合理论和数值分析结果,结合现场试验实测应力数据,确定索力的纵向传递角度规律,为后续规范修订提供理论和实践基础。

2 肋板结构考虑剪力滞后效应的微分方程及其解

2.1 计算基本假定

建立局部坐标系如图1所示。坐标原点O位于横截面对称面上,Ox轴平行于截面中性轴(纵桥向);为避免在分析过程中出现不必要的扭转及横向位移,将Oxz平面设置为与梁横截面对称面重合。伸长率ε和剪切应变γ的下标分别表示应变方向以及所属梁体部位;下标w和f分别表示腹板和翼板。

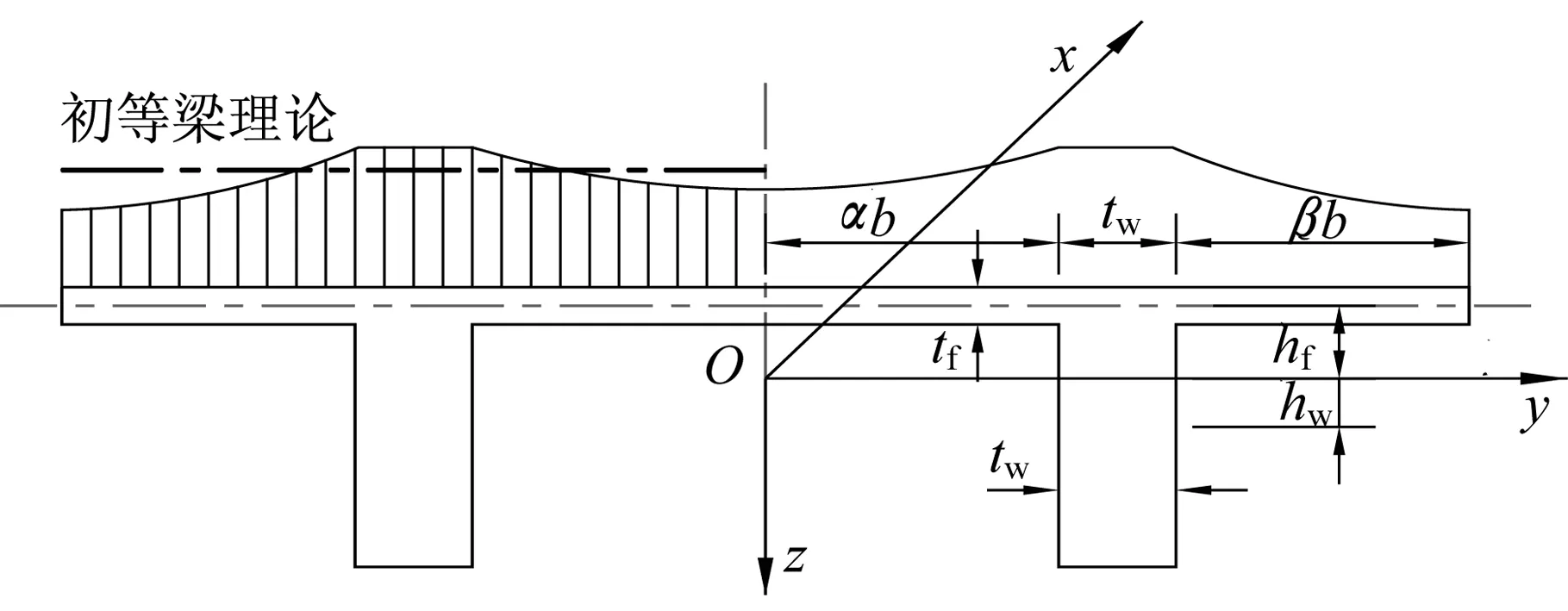
图1 截面几何参数及应力状态Fig.1 Geometry and distribution of stress in slab

相比双主肋梁整体高度,混凝土翼板厚较小,因此可以假设在板厚范围内,描述翼板截面应力分布不均轮廓线的修正E.Reissner函数[18]在z方向上保持不变,仅仅是关于y坐标的函数R(y,z)≅R(y);应用能量变分方法分析时,梁的竖向整体挠度用ω(x)表示,梁的纵向整体位移用u(x)表示,故有

uf(x,y)=u(x)-zω′(x)+R(y)ψ(x)

(1)

uw(x)=u(x)-zω′(x)

(2)

式中,ψ为翼板中面的最大纵向位移差函数,非位移变量;b为翼板净宽的1/2,αb+βb;z为截面形心至计算点的竖向距离;uf,uw分别为翼板与腹板x方向位移。

在建立梁的局部坐标系的过程中,考虑截面几何尺寸和荷载的对称性,定义函数R关于z坐标轴对称,通常采用多项式形式[19]:

(3)

在应变计算中,腹板仍采用梁的变形计算方法(按平截面假定),不考虑腹板的剪切变形。对于翼板,板的竖向纤维无积压,即εz=0。板平面外的剪切变形γxz与γyz及横向应变εy均很小,可忽略不计。翼缘板中面的最大纵向位移差函数ψ,需要从平衡方程中求解。式中,′表示变量对x的导数;L为梁的计算长度;A为梁的横截面面积。

2.2 平衡方程的建立

根据位移方程,建立梁的力学几何方程,翼板正应变及剪应变为

(4)

(5)

腹板正应变:

(6)

式中,R,y表示翼板中面的最大纵向位移差函数对y的导数。

利用胡克定律建立翼板及腹板的力学物理方程,可以得到翼板x方向应力σx,f,Ozy平面内剪应力τxy,f和腹板x方向应力σx,w:

σx,f=Ecεx,f=Ec(u′-zω″+Rψ′)

(7)

(8)

σx,w=Ecεx,w=Ec(u′-zω″)

(9)

式中,E为梁弹性模量;G为梁剪切模量;ν为混凝土泊松比。

根据最小势能原理,在外荷载作用下,结构处于平衡状态。当有任何虚位移时,体系总位能的一阶变分δ为零,即

Π=V-Γ

(10)

δΠ=δ(V-Γ)=0

(11)

式中,V为体系的应变能;Γ为外力势能。

梁承受压弯外荷载时的外力势能:

(12)

式中,M及N分别表示作用在梁上的弯矩和轴力。

梁的体系应变能由两部分构成,其中翼板与腹板的应变能分别为

(13)

(14)

将式(4)-式(9)代入外力势能及体系应变能表达式(12)-式(14)。由最小势能原理δΠ=0并作分部积分后,得到压弯荷载作用下,双主肋混凝土梁的平衡微分方程及边界条件:

(15)

(16)

(17)

(18)

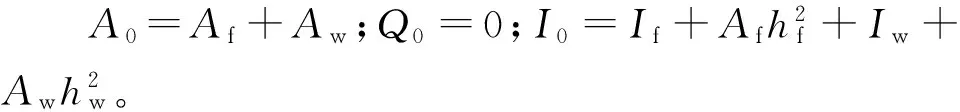
与E.Reissner函数R(y)相关的积分惯量定义如下:

(19)

平衡微分方程及边界条件式(15)-式(18)可以改写为:

EcQ0u′+EcSRψ′+EcI0ω″+M=0

(20)

Ec[SRω‴+IRψ″+QRu″]-GcψIdR=0

(21)

EcA0u′+EcQ0ω″+EcQRψ′-N=0

(22)

Ec[SRω″+IRψ′+QRu′]δψ|x∈[0,L]=0

(23)

从力学物理意义上分析:式(20)表示梁在z方向的平衡状态;式(21)表示横截面出现应力分布不均匀状态,这种状态在截面内的自平衡;式(22)则表示梁在x方向的平衡状态。

联合求解平衡方程,可以得到关于翼板中面的最大纵向位移差函数ψ的四阶微分方程:

ψ″-k2ψ=n[αM′-βN′]

(24)

ω″(x)=-(M+EcSψψ′)/(EcI0)

(25)

u′(x)=-(-N+EcQRψ′)/(EcAo)

(26)

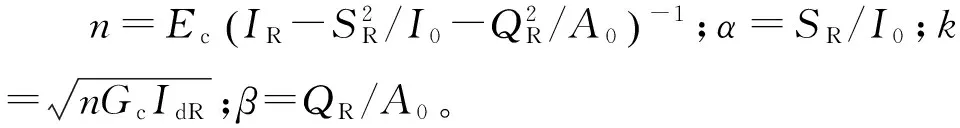
方程式(24)的一般解形式为

ψ(x)=n(C1sinhkx+C2coshkx+ψ*)

(27)

其中,ψ*为与M′和N′分布有关的微分方程特解,系数C1与C2由梁的边界条件及连续条件确定:当梁固结时ψ=0,δψ=0;当梁为非固结时,边界条件满足方程式(23)。

由式(25)、式(26)可见,梁的曲率-弯矩与线应变-轴力的关系已经不再符合欧拉-伯努利梁理论,截面内应力分布不均匀,使得梁的有效刚度降低,增大了梁的变形。

如图2所示的等截面悬臂梁,自由端面距离梁截面形心Δ处,作用集中荷载T:其竖向分力为P,水平分力为N。梁上作用均布荷载q。

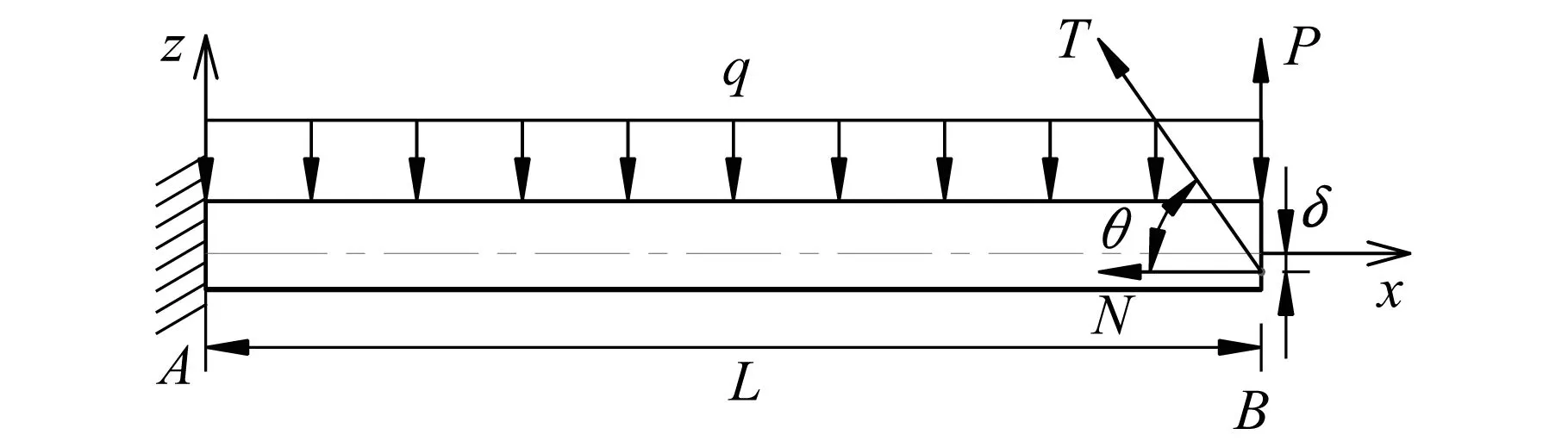
图2 承受压弯荷载悬臂梁计算图示Fig.2 Calculation diagram of cantilever beam subjected to compact-bending load

将悬臂梁弯矩M、剪力Q和轴力N表达式,代入式(24)并加以推演可得:

(28)

式(28)在固定端,满足边界条件ψ=0,而在自由端,满足:

(29)

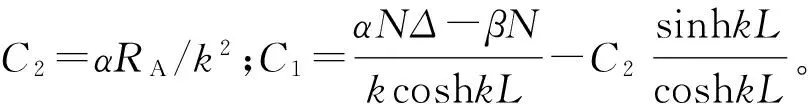
对式(25)-式(27)分别求一阶导数,代入式(7),得到翼缘板的应力分布:

σx,f=(zM/I0+N/A0)+

Ecψ′[Sψ/I0-QR/A0+R]

(30)

图3 桥跨布置图(单位:m)Fig.3 Layout of bridge span (Unit:m)

2.3 常规肋板截面的轴力传递规律解析解分析

在建的辰塔公路越黄浦江大桥,主桥为双塔双索面混凝土梁斜拉桥,半漂浮体系,跨径布置为(49.5+75.5+296+75.5+49.5)m;斜拉索纵向立面采用扇形布置,共84对索;主梁采用预应力混凝土双主肋断面,主梁宽度34.6 m,截面中心点梁高2.8 m,主肋梁高2.55 m,桥面设2.0%双向横坡。结构布置及断面几何尺寸如图3、图4所示。

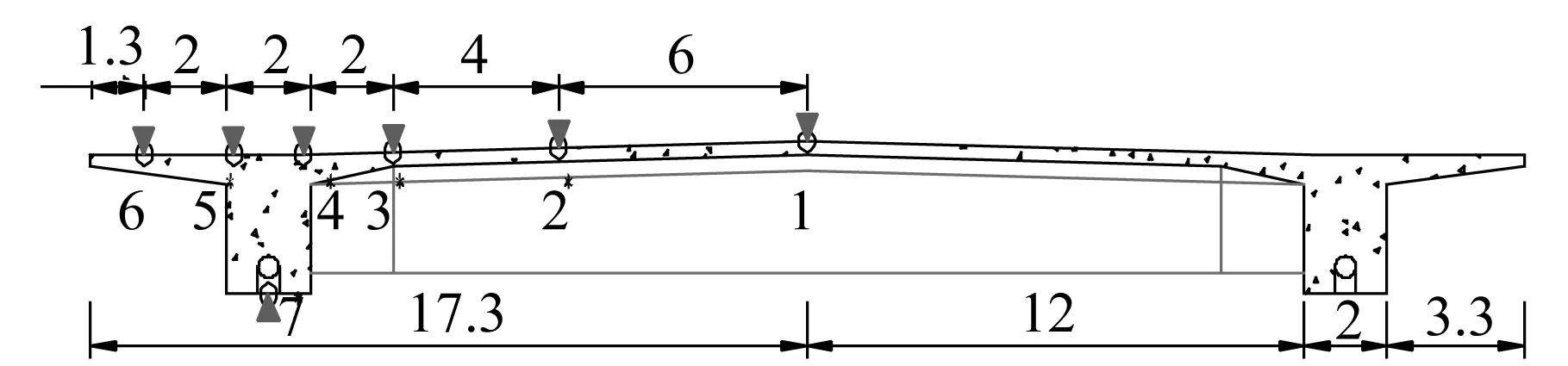
图4 梁截面几何参数(单位:m)Fig.4 Geometry of cross section (Unit:m)

主梁采用复合型前支点挂篮,全断面一次性浇筑施工,标准节段长6.6 m。斜拉索的第一次以及第二次张拉,都是作用在挂篮上,索力通过挂篮的锚固系统及止推机构传递至主梁,而非直接作用在主梁的锚固点。因此选择索力转换后,斜拉索第三次张拉的工况,对主梁受力进行分析。

利用2.2节解析解,根据现场实测索力数据[20],得到主梁截面应力变化规律如图5所示。当剪力滞系数λ≅1.0时,意味着截面应力分布趋于均匀,索力作用基本扩散至整个截面,符合初等梁理论。为了进一步了解压弯荷载对传递距离的影响,选择主桥14#斜拉索第三次张拉工况:在索力不变的情况下,改变斜拉索角度θ,即改变水平分力与竖向分力的比值,分析其对荷载传递的影响。为消除轴向荷载偏心对参数分析的影响,将轴向荷载作用在梁截面形心Δ=0处,剪力滞系数变化如图6所示。

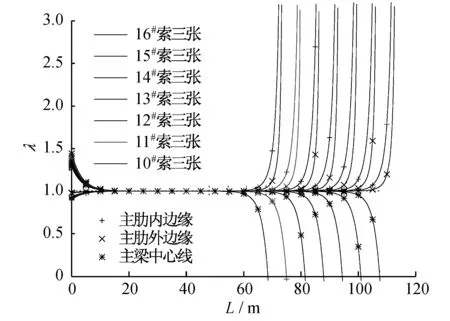
图5 索力作用下截面各处λ的变化Fig.5 Variation of λ under cable load

根据解析解理论分析结果可以看出:轴向荷载对荷载作用点附近区域截面应力分布影响较为明显;在远离作用点一定范围后,影响逐渐减弱,因此将轴向荷载的影响范围,认为是轴向荷载的传递长度或传递扩散角度,是一种可行的研究思路;图5、图6主肋内外侧λ不同,索力在截面内的分配,应该与截面各区域刚度大小有关:主肋内侧桥面板相比外侧人行道翼板刚度大,因此分担的内力要更多;索力在传递约三个节段19.8 m后,截面应力趋于平均,与K.Roik等[15]得到结论吻合;当N/P增大时,集中荷载扩散的角度有逐渐增大的趋势。

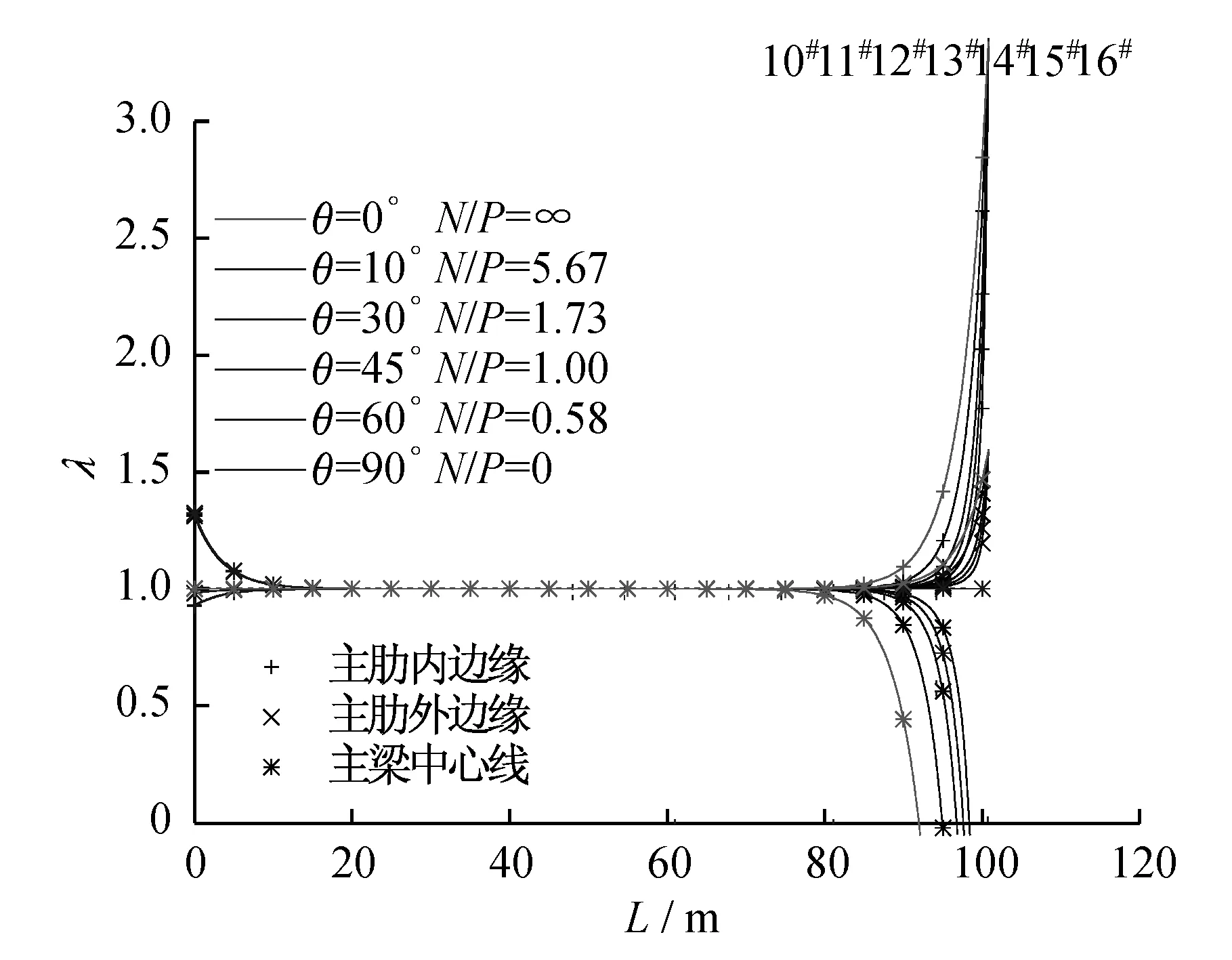
图6 N/P对截面各处λ的影响Fig.6 The influence of N/P on the λ

3 有限元数值分析

3.1 分析模型

为了进一步分析索力的传力机理,验证解析解结果的有效性,采用ANSYS实体有限元参数化模型,通过程序“ealive”与“ekill”处理功能,模拟主桥悬臂浇筑施工过程。

考虑到结构形式和荷载的对称性,整体计算模型取1/2进行分析,如图7所示。计算采用8节点Solid45单元,使用mapped映射网格划分,单元尺寸控制在7～15 cm,在分析中,将整个结构视为匀质弹性体,混凝土弹模取Eh=3.55×107MPa,泊松比ν=0.167。斜拉索采用Link180单向受拉构件模拟,根据现场实测索力,施加初应力。模型中没有考虑主塔,斜拉索塔上的锚固点采用位移约束。在塔根部设置对称约束;考虑自重荷载,取重力加速度9.8 m/s2。

3.2 结果分析

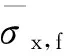
(31)

式中,η表示截面有效宽度be占桥面总宽度bc的比例,积分区域如图7所示。

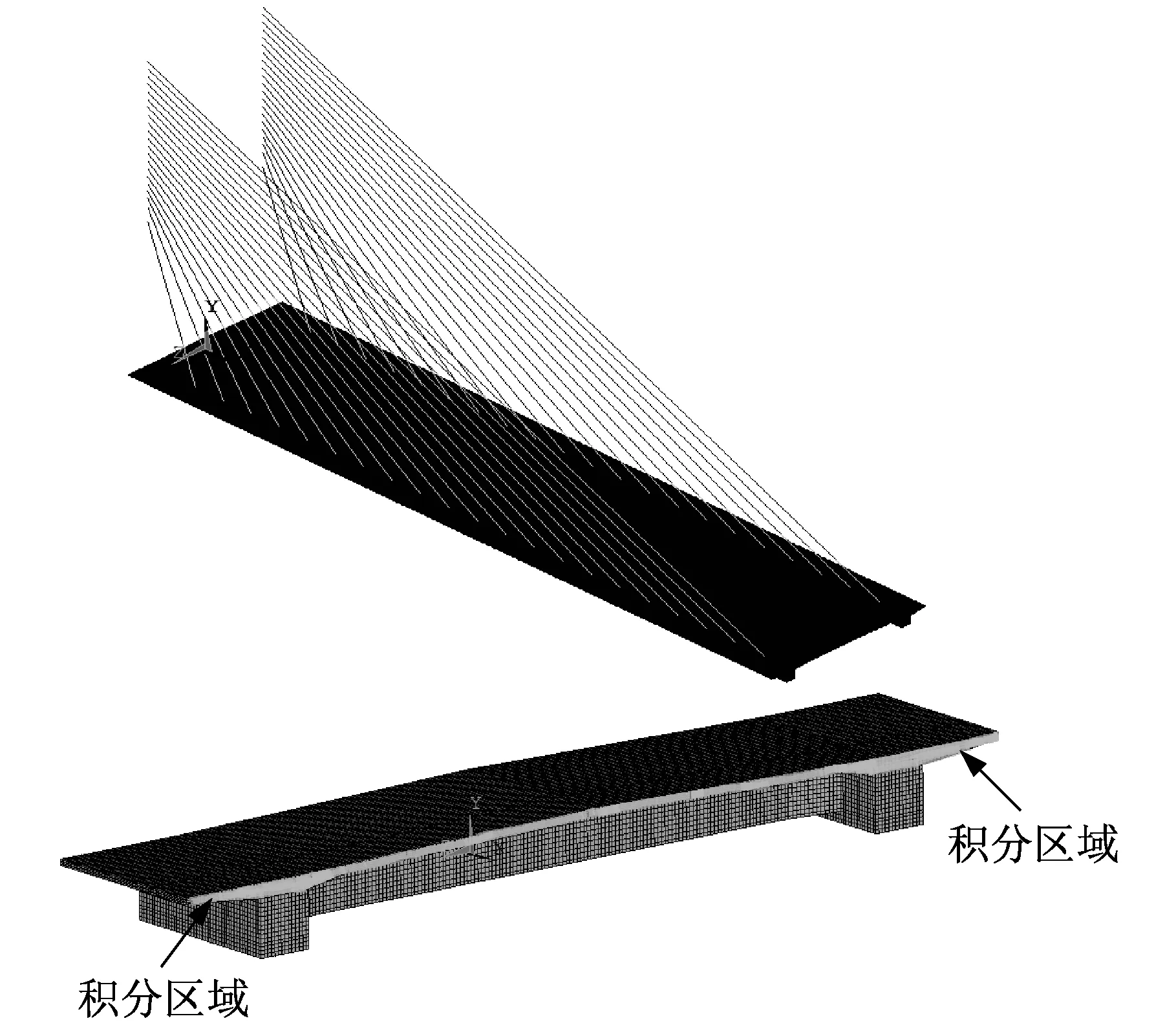
图7 整体及标准节段有限元模型Fig.7 The finite element model of the bridge and the girder segment

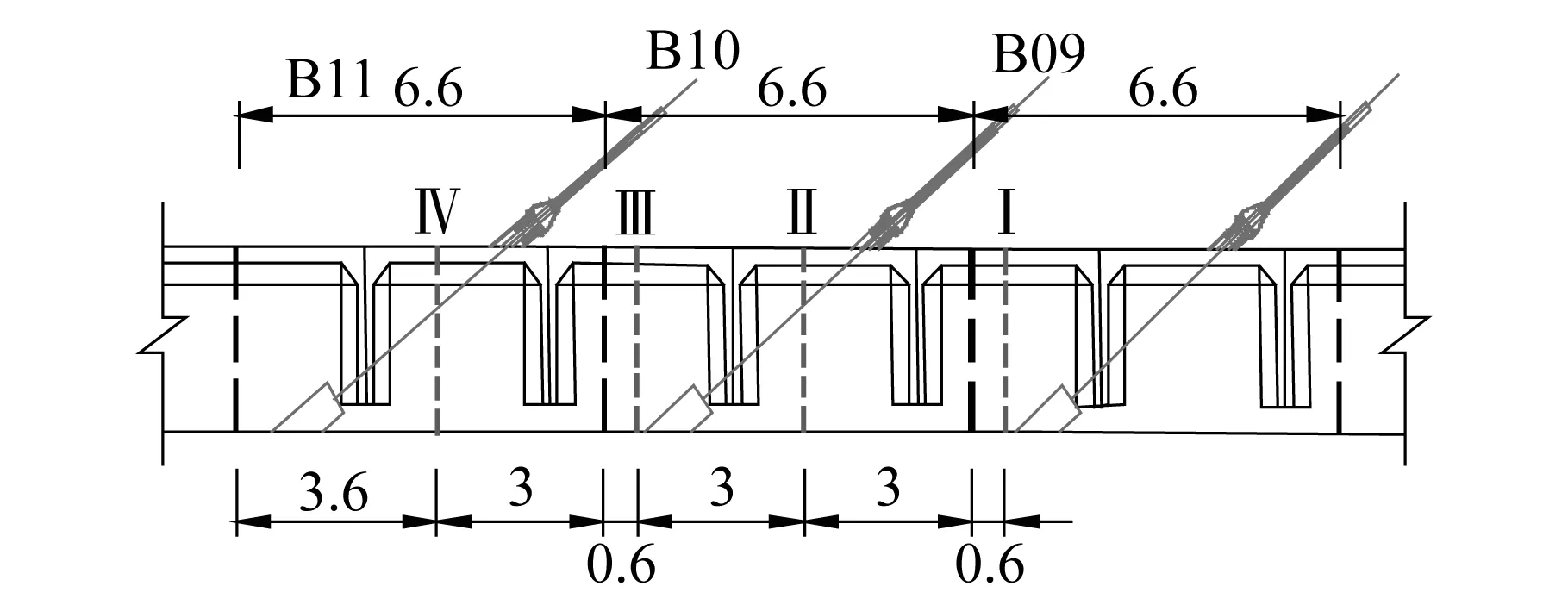
图8 计算截面(单位:m)Fig.8 Geometry of cross section (Unit:m)

选择图3与图8对应所示的Ⅰ～Ⅳ截面,按照悬臂施工顺序,进行η值的计算,分析标准节段在斜拉索第三次张拉工况下,桥面板有效宽度的变化规律,其中Ⅱ和Ⅲ截面均在第10标准段,Ⅰ、Ⅳ分别在第9与第10标准段内。计算结果如图9所示:随着施工悬臂长度增加,桥面板越来越多的参与整个截面的受力;当滞后3～4个节段后,相应截面有效宽度的增加速率逐渐趋缓,由17%降至5%以下。

桥面板对肋板结构截面特性贡献在30%上下,考虑到有效宽度,其对截面特性的贡献在10%左右。从Ⅱ和Ⅲ断面桥面板有效宽度系数来看,横梁对桥面有效宽度的影响很小;当Ⅰ、Ⅱ和Ⅲ、Ⅳ截面具有相近的η值时,均各自相差一个标准段工况。在同一工况下,对一个标准段范围内的有效宽度取相同数值而进行施工过程仿真计算,是可行的。同时在分析过程中发现,翼缘板大部分参与本节段整个断面的施工受力,因此全断面一次性浇筑,有利于结构的整体受力。

图9 标准段斜拉索第三次张拉工况截面有效宽度变化Fig.9 Variation of effective width under the third cable-tension

由上述有限元模型计算得到的桥面板正应力,根据桥轴线附近零应力区域和应力等值线的变化规律,绘制索力传递扩散的趋势线,并结合图4断面几何参数,计算扩散角度值详见表1。

表1扩散角度

Table 1 Angle of force propagation

随着悬臂长度的增加,结构整体柔度变大,局部效应逐步减弱,越来越趋近于杆系单元受力,集中荷载的扩散角度有逐渐增大的趋势。根据有限元计算结果,对于综合考虑竖向、轴向及自重荷载作用下,集中荷载沿主肋的两侧以α=26.5°～32°角度向桥面板传递,上、下限分别与AASHTO规范[16]、DIN规范[17]接近。实际过程中,仅有轴向荷载作用的工况较少,基本是多种荷载共同作用,因此建议轴向荷载作用下分离式双主肋断面桥面板有效分布宽度近似的按照DIN规范角度计算,取α=26.5°,计算结果偏于安全。

4 实桥现场试验

4.1 传感器布设

试验监测中采用长沙金码高科技实业有限公司生产的JMZX-215AT智能弦式应变传感器和配套的综合测试仪。传感器布设在主跨1/4截面附近,避免梁体在塔梁根部复杂约束边界条件,同时避免主跨中附近应力峰值截面,全桥测点断面如图3中Ⅰ～Ⅳ截面所示。

为避开应力集中位置,传感器布置在非扩大截面的普通钢筋上,同时避开节段拼缝位置,离开斜拉索锚固点一定距离。且顺桥方向各测试断面要保持一定距离,不能过大或者过小,能够比较准确的反映索力纵向传递规律,因此测试断面纵桥向分布如图10所示。考虑到截面应力基本按照抛物曲线形式分布,因此传感器按照一定距离比例布设,非等间距设置,如图11所示。

图11 现场传感器布设Fig.11 Layout of sensor in situ

4.2 试验数据分析

为尽量减少收缩、徐变对实测数据的影响,选取斜拉索第三次张拉前、后两个工况数据进行对比。并且该工况下,斜拉索索力直接作用在主梁的锚固点,而非通过前支点挂篮的锚固系统传递至主梁,结构受力明确。三张前后,现场实测索力变化值详见表2。

表2索力变化值

Table 2 Variation of cable force

将实测索力值施加在有限元模型中,并与斜拉索张拉前、后,测试断面应变变化值进行对比,如图12所示。多数测点的试验值与理论值吻合得较好,整个断面应力分布的变化规律与计算值基本一致。随着斜拉索距离测试断面越来越远,索力的影响范围逐渐扩散至整个截面,并且各索力的作用相互叠加,应变的变化越来越复杂。以Ⅰ断面为例,斜拉索三张前、后,截面测点平均应变以及主肋处应变与平均应变的比值,详见表3。

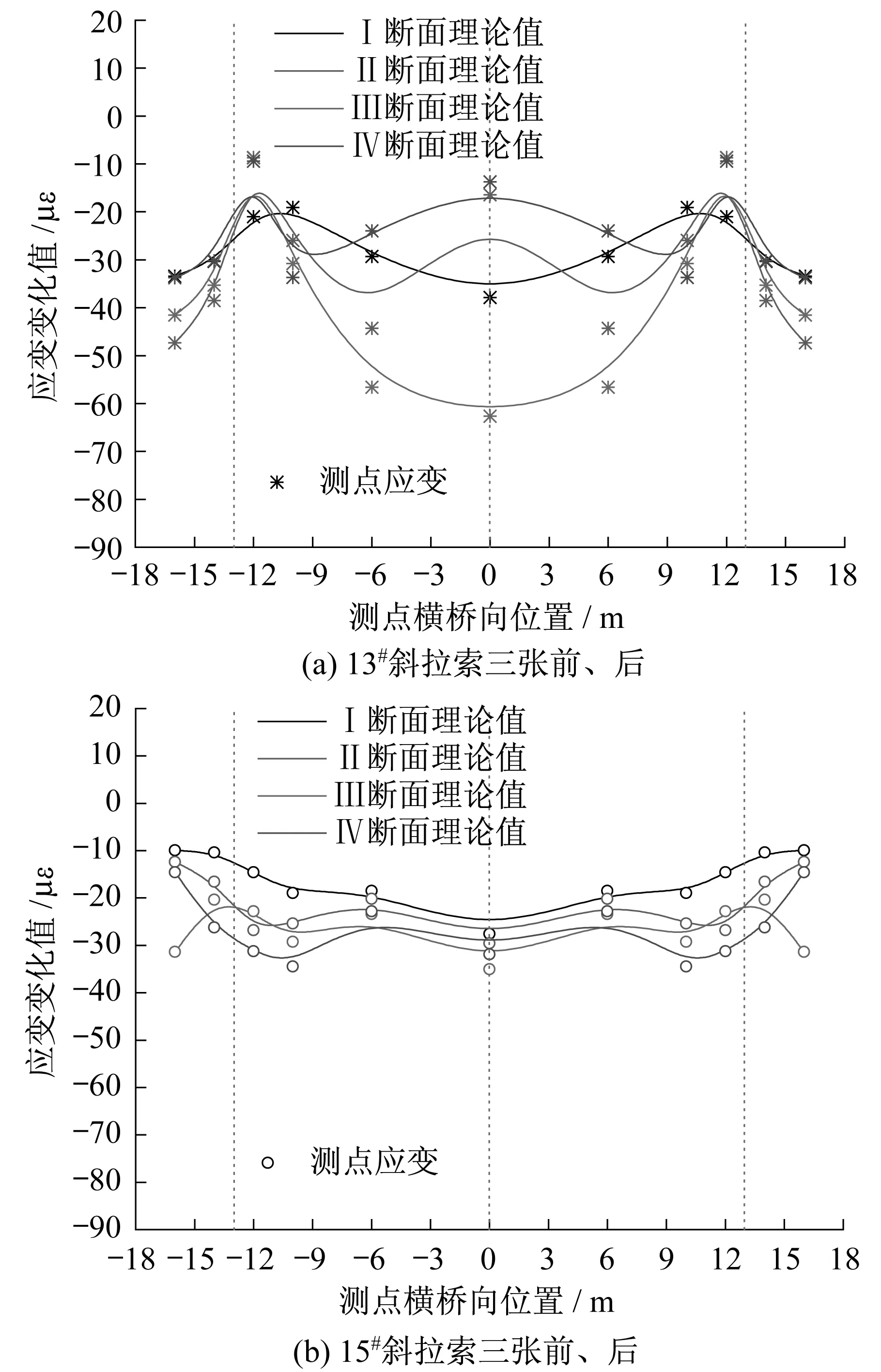
图12 截面应变变化对比Fig.12 Variation of strain during the tensing process

表3I截面应变变化值

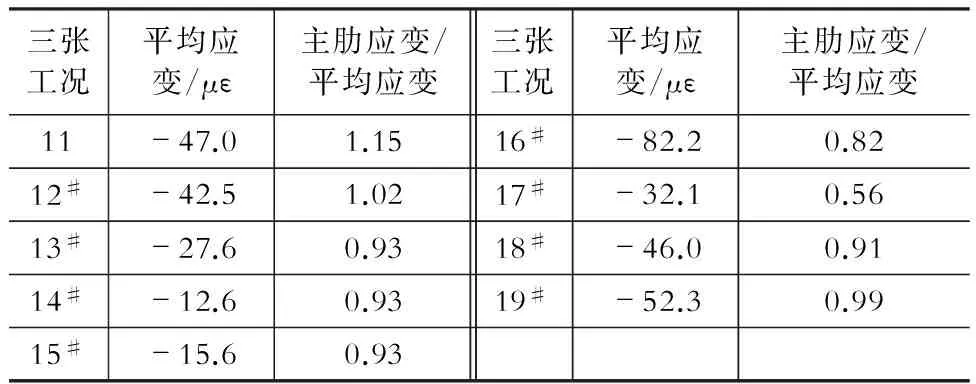
Table 3 Variation of strain in section I

注:16#及17#工况,现场个别测点数据异常,以红体示出。

当12#、13#斜拉索张拉时,Ⅰ断面测点正应变变化值基本趋于稳定;当15#斜拉索张拉时,Ⅰ～Ⅳ断面测点正应变变化值均趋于稳定。索力在经过约四个标准段的传递后,已经基本扩散至整个截面。观察图中主肋内、外侧应变变化的趋势,靠近主肋内侧的截面应变变化要大于主肋外侧,从另一方面印证2.3节的结论。

5 结 论

本文依托目前在建的上海市辰塔公路越黄浦江大桥主桥,通过理论分析并结合数值模拟,以及现场实桥试验,分析了双主肋梁截面斜拉索索力传递机理,得到以下结论:

(1) 随着悬臂施工阶段的增加,桥面长度方向板越来越多的参与整个截面的受力;索力对有效宽度的影响,基本保持在3～4个节段以内;实际设计过程中,可以取3个节段来计取索力的影响。

(2) 双主肋梁结构的横梁对桥面有效宽度的影响较小;在悬臂施工过程中,每个标准节段的有效宽度可近似取同一数值进行施工仿真计算。

(3) 建议我国现行设计规范,增加轴向荷载扩散角度的定义:分离式双主肋断面桥面板有效分布宽度近似的按照DIN规范[17],取α=26.5°,计算结果偏于安全。

[1] 程翔云,罗旗帜.箱梁在压弯荷载共同作用下的剪力滞[J].土木工程学报,1991,24 (1):52-64.

Cheng Xiangyun,Luo Qizhi.Shear lag effect of thin-walled box girder under compact-bending load [J].China Civil Engineering Journal,1991,24(1):52-64.(in Chinese)

[2] 蔡松柏,程翔云,邵旭东.Π形梁剪力滞效应的解析解[J].工程力学,2003,20(5):82-86.

Cai Songbai,Cheng Xiangyun,Shao Xudong.An analytical solution for shear lag effects of flat-archshaped beam bridge [J].Engineering Mechanics,2003,20(5):82-86.(in Chinese)

[3] 韦成龙,曾庆元,刘小燕.肋板结构受压构件的剪力滞效应分析[J].力学与实践,2001,23(2):41-43.

Wei Chenglong,Zeng Qingyuan,Liu Xiaoyan.Shear lag effect analysis for beam-and-slab deck under axial load [J].Mechanics in Engineering,2001,23(2):41-43.(in Chinese)

[4] 陈德伟,白植舟.斜拉桥施工中主梁的剪力滞分析[C].南京:第十四届全国桥梁学术会议论文集,2000:605-612.

Chen Dewei,Bai Zhizhou.Shear lag analysis of cable-stayed bridge during the construction of the main girder [C].Nanjing:The 14th National Bridge Conference Proceedings,2000:605-612.(in Chinese)

[5] 魏红一.斜拉桥施工全过程主梁有效宽度分布模式研究 [D].上海:同济大学,2004.

Wei Hongyi.Study on effective distribution width of main firger of cable stayed bridge considering the whole construction procedure [D].Shanghai:Tongji University,2004.(in Chinese)

[6] 李华,任剑莹.压弯荷载共同作用下肋板结构剪力滞分析[J].桥梁建设,2005,4:24-30.

Li Hua,Ren Jianying.Analysis of shear lag of ribbed slab structure under combined bending and axial loading [J].Bridge Construction,2005,4:24-30.(in Chinese)

[7] 张永健,王达,黄平明.斜拉桥Π形主梁剪力滞影响因素分析[J].建筑科学与工程学报,2008,25(1):116-121.

Zhang Yongjian,Wang Da,Huang Pingming.Effect factor analysis of shear lag of cable-stayed bridge with Π-shaped main girder [J].Journal of Architecture and Civil Engineering,2008,25(1):116-121.(in Chinese)

[8] 李乔,唐亮,黄道全,等.斜拉桥Π形截面PC主梁剪力滞模型试验研究[J].桥梁建设,2004,5:7-10.

Li Qiao,Tang Liang,Huang Daoquan,et al.Model test and study of shear lag of prestressed concrete main girder of cable-stayed bridge with Π-shape cross section [J].Bridge Construction,2004,5:7-10.(in Chinese)

[9] 万臻,李乔,毛学明.Π形截面主梁斜拉桥剪力滞效应试验研究[J].西南交通大学学报,2004,39(5):623-627.

Wan Zhen,Li Qiao,Mao Xueming.Experimental research of shear lag effect of cable-stayed bridge with Π cross-section main girder [J].Journal of Southwest Jiao Tong University,2004,39(5):623-627.(in Chinese)

[10] 周绪红,狄谨,戴公连.大跨径预应力混凝土斜拉桥主梁节段模型的研究[J].土木工程学报,2005,38(3):59-63.

Zhou Xuhong,Di Jin,Dai Gonglian.Study on segmental model of girder of long-span prestressed concrete cable-stayed bridge[J].China Civil Engineering Journal,2005,38(3):59-63.(in Chinese)

[11] 张永健,黄平明,贺志高.Π形梁斜拉桥主梁剪力滞特性分析[J].长安大学学报(自然科学版),2008,28(6):51-54.

Zhang Yongjian,Huang Pingming,He Zhigao.Test on shear lag of cable-stayed bridge with Π-shaped cross section main girder [J].Journal of Chan an University (Nature Science Edition),2008,28(6):51-54.(in Chinese)

[12] 中华人民共和国交通部.JTG/T D65-01—2007 公路斜拉桥设计细则[S].北京:人民交通出版社,2007.

Ministry of Transport of the People’s Republic of China.JTG/T D65-01—2007 Guidelines for design of highway cable-stayed bridge[S].Beijing:China Communications Press,2007.

[13] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2012.

Ministry of Transport of the People’s Republic of China.JTG D62—2004 Code for design reinforced concrete and prestressed concrete bridges and culverts[S].Beijing:China Communications Press,2004.

[14] 上海市政工程设计研究总院.桥梁设计工程师手册[M].北京:人民交通出版社,2007:807- 808.

Shanghai Municipal Engineering Design Institute.Manuals for bridge design engineer[M].Beijing:China Communications Press,2007:807- 808.

[15] Roik K,Albrecht G,Weyer U.Schrägseilbrücken [M].Berlin:Ernst & Sohn.1980.(in German)

[16] AASHTO.AASHTO LRFD bridge design specifications (SI) [S].Washington (DC):American Association of State Highway and Transportation officials,2007.

[17] DIN.DIN 1075.Concrete bridges:Dimensioning and construction [S].Berlin:Deutsches Institute Fur Normung,1981.

[18] 项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.

Xiang Haifan.Advanced structural theory of bridge [M].Beijing:China Communications Press,2001.(in Chinese)

[19] 张士铎,邓小华,王文洲.箱型薄壁梁剪力滞效应[M].北京:人民交通出版社,1998:80-82.

Zhang Shiduo,Deng Xiaohua,Wang Wenzhou.Shear lag effect in thin-walled box girder [M].Beijing:China Communications Press,1998:80-82.(in Chinese)

[20] 陈德伟,李欣然.辰塔大桥施工监测控制报告[R].上海:同济大学,2015.

Chen Dewei,Li Xinran.Summary report of construction monitor and control for Chenta bridge [R].Shanghai:Tongji University,2015.(in Chinese)