消能减震元件失效对框架核心筒结构极限性能的影响

陈煜棪 钱 江

(同济大学土木工程防灾国家重点实验室,上海 200092)

0 引 言

在过去30多年的结构抗震控制研究中,消能减震、隔震技术已逐渐趋于成熟。目前工程中较常采用的消能减震装置主要有黏弹性阻尼器、粘滞阻尼器、金属阻尼器和摩擦阻尼器[1]。这些消能减震元件可以灵活安装于各类建筑结构的不同部位。对于带剪力墙的结构,将消能减震元件安置在连梁中段而组成的消能连梁就是常见的一种形式[2]。

消能减震元件通过自身的位移或形变消耗地震波传来的能量,以达到控制结构响应并减少结构破坏的目的。不论是在以往的理论研究及振动台试验中,还是在地震的检验下,消能减震元件的表现都较为优越,使得其应用越来越广泛。然而,在极端灾害中,消能减震元件却出现了意想不到的问题[3]。2011年3月11日,日本东北地区发生了震级为M9.0级的强烈地震,中日联合考察团对震害的破坏程度和影响进行了研究考察[3],薛松涛等人报道了仙台某建筑的油阻尼器发生严重破坏的案例[4-5],指出了减震系统失效后高层建筑的安全性是今后面临的重大挑战[6]。因此,在极端荷载下,需要考虑消能减震元件的破坏和失效状态,并研究该类附属结构的破坏失效会对建筑结构整体产生何种影响。

本文将以带软钢阻尼器消能连梁的混凝土框架核心筒结构为研究对象,分析探讨在极端荷载作用下,阻尼器连梁失效对结构整体极限性能的影响。

1 阻尼器失效

日本隔震协会(JSSI)在3·11地震后的调查中发现[6]:强震后,部分金属阻尼器受到了不同程度的损伤,如固定金属阻尼器的高强螺栓发生了松动,金属阻尼器已经进入屈服阶段,产生残余变形,造成了耗能能力的降低等。此外,根据力学知识和相关试验可知,设置在连梁中的软钢阻尼器,还可能会产生构件的弯曲破坏或剪切破坏[7]。

由此看出,连梁中的软钢阻尼器,存在多种损伤或失效的可能。对于不同的损伤失效模式和损伤失效后的残余性能,目前还缺乏完善、系统的研究和检验。因此,本文暂不考虑阻尼器不同的损伤失效模式,且由于失效位置与数量的随机性和不确定性,先假定所有的阻尼器连梁均发生失效,无残余性能,并在模型中拆除全部的带阻尼器连梁段。经过该方法处理的结构在后文研究中称为“阻尼器失效结构”,而阻尼器全部完好无损的结构称为“原结构”。

2 基于IDA方法的地震易损性分析

基于性能的地震工程研究,目前已经形成较为完整的理论实践体系,通过估计和计算分析结构在不同危险性水平的地震动下结构的抗震需求和能力,达到对结构性能评价的目的。其计算分析的方法有非线性静力分析、多模态推覆分析、非线性动力分析、增量动力分析等[8],本文采用增量动力分析(IDA)方法。

IDA方法以非线性动力时程分析为基础,将地震波在某一范围内进行调幅,进行一系列时程分析,得到不同地震动强度下结构的响应,从而涵盖了结构从弹性到塑性的整个过程[9-10]。对多条地震动记录所得的IDA数据结果进行概率统计分析,可以进一步得到对结构的地震易损性进行评估结果。

地震易损性可反映出地震动强度和结构破坏程度之间的关系,并用地震易损性曲线来表示。其横坐标为地震动强度(IM),纵坐标为结构响应达到或超过某种性能水准等级的概率。本文以多条记录下的IDA方法为基础,通过建立结构在不同性能水准等级下的地震易损性曲线,来评价阻尼器失效对结构极限性能的影响。

3 算例分析

本文算例为某30层混凝土框架核心筒结构,其连梁中段设置有软钢阻尼器。该算例借鉴了日本清水建设集团的9栋带软钢阻尼器连梁的框架核心筒结构[11]的结构布置形式,如图1(a)所示,平面尺寸为38.3 m×30.8 m,平面布置如图1(b)所示,构件尺寸见表1。抗震设防烈度为8度(0.2g),设计场地分组第二组,Ⅲ类场地。结构基本周期2.595 s,为X方向平动。首先在结构设计软件PKPM中进行建模,并按《混凝土结构设计规范》(GB 50010—2010)进行配筋计算,再将计算模型导入Perform 3D中进行弹塑性时程分析。

表1构件尺寸信息

Table 1 Size information of components mm

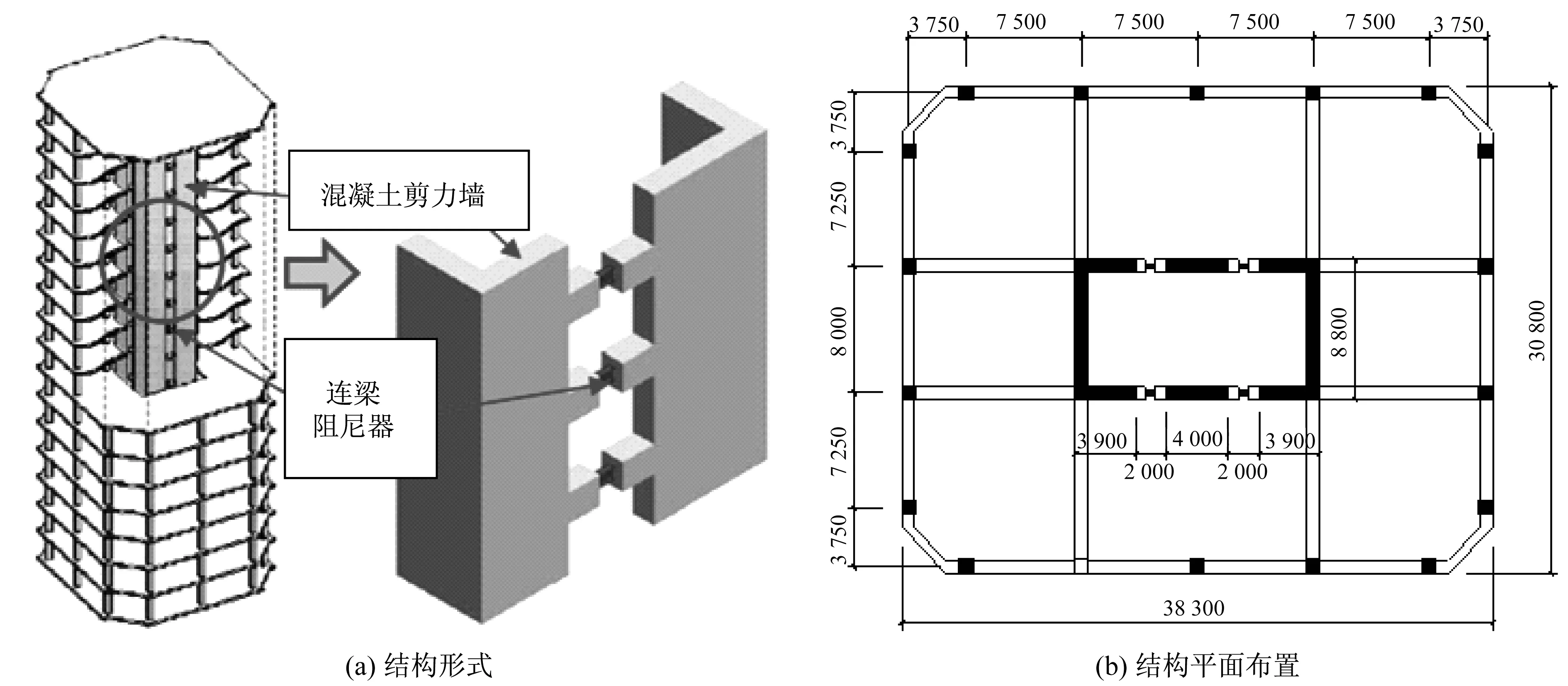
图1 结构形式及布置示意图Fig.1 Form and layout of the structure

3.1 地震动选择

地震波的合理选取是保证IDA分析有效的前提。以规范的设计反应谱为标准,本文共从PEER地震动数据库中选取了11条地震波,详见表2。设计反应谱和所选地震动加速度反应谱见图2。依据场地类型,所选地震波的剪切波速峰值均在200 m/s左右。震级均不小于6级,包括远、近场地。为保证使结构产生较明显的响应,所选地震波的峰值加速度均大于0.2g,峰值速度均大于15 m/s。震源机制为走滑断层或逆冲断层。

3.2 增量动力分析

本文采用Perform 3D,以弹塑性时程分析作为基础,进行增量动力分析。其中,梁构件的中部采用钢筋混凝土梁截面组件,两端采用弯曲塑性铰来模拟;软钢阻尼器为工字型钢梁截面,中间设置剪切塑性铰,两端设置弯曲塑性铰;柱构件的中部采用钢筋混凝土梁截面组件,两端采用非线性的柱纤维截面;墙构件采用非线性的通用纤维墙截面。

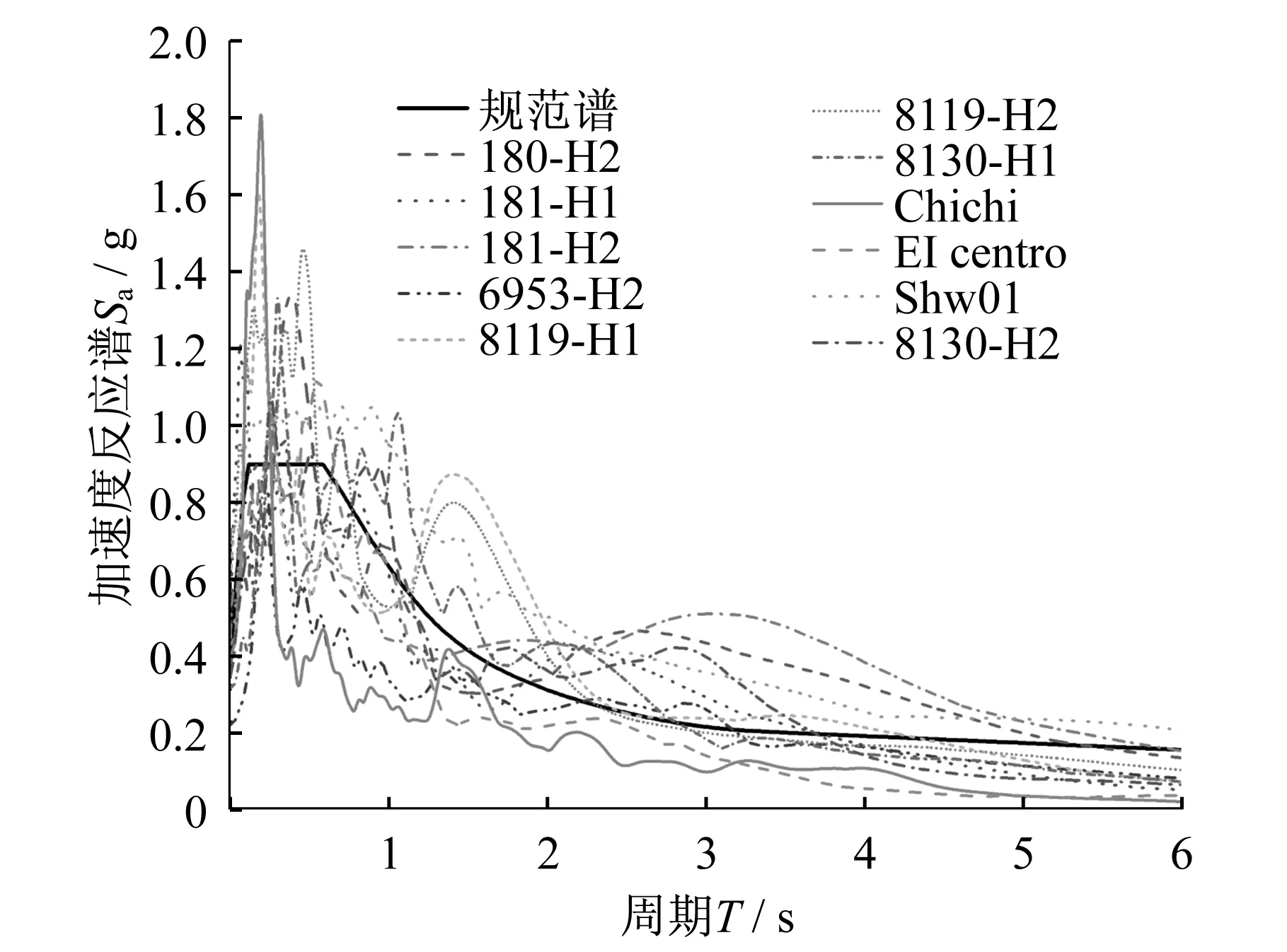
图2 地震动加速度反应谱及设计反应谱Fig.2 Acceleration response spectra of design and the selected earthquake records (ζ=0.05)

表2地震记录及其地震动参数

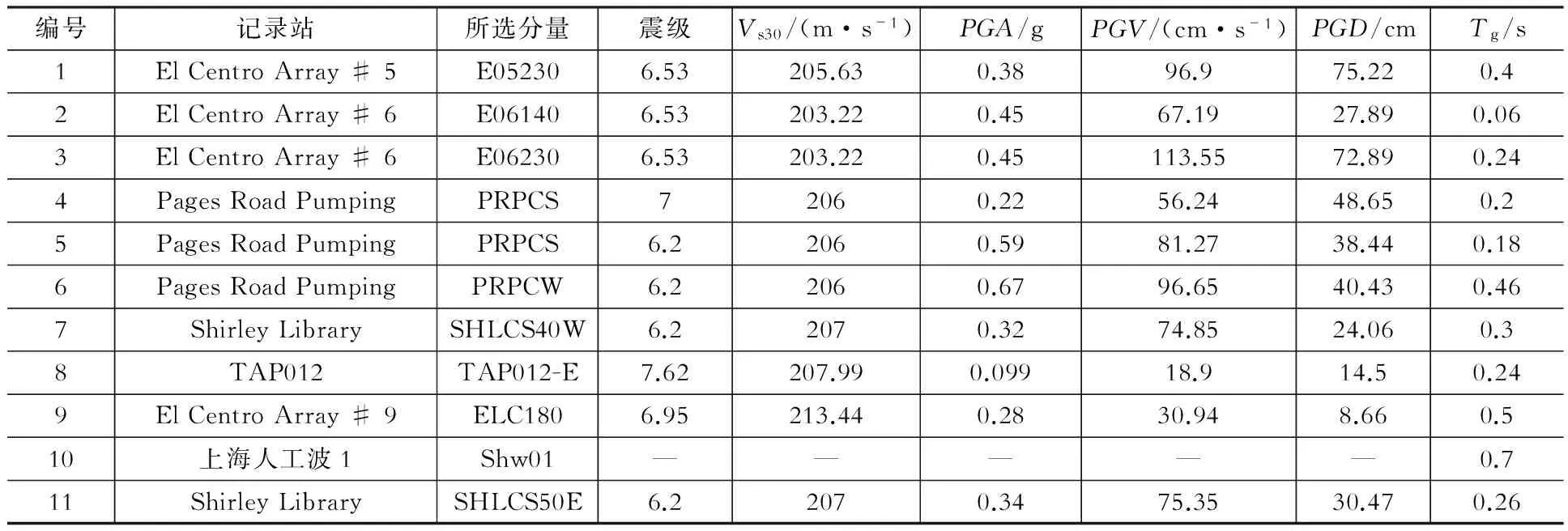
Table 2 Seismic record and the ground motion parameter

IDA分析中的地震动强度IM,用结构基本周期所对应的加速度反应谱值Sa(T1,5%)来表示,在计算时采用固定步长0.1g。结构损伤参数DM由结构的最大层间位移角 表示,加载时,按文献[7]的标准来判断继续调幅或是终止。将计算所得的一系列IM-DM离散点分别进行三次样条插值,得到IDA曲线簇,如图3所示。

图3 IDA曲线簇Fig.3 IDA curves of the structures

IDA曲线簇具有一定的离散性和差异性,本文用MATLAB对IDA数据进行处理分析。IM-DM的关系是一个随机函数,对任意的DM=f(IM),通常假定DM对IM的条件概率满足对数正态分布[12]。若η,β分别对应于IM=x条件下DM的中位数和标准差,则η·e-β,η,η·eβ就对应着该条件下DM值的三个分为数,其超越概率分别为16%、50%、84%。由此,可以得到与这三个分位数相应的IDA曲线,如图4所示。

图4 IDA分位数曲线Fig.4 Fractile IDA curves of the structures

从图4可以看出,对于任一分位数曲线而言,相比于原结构,在相同的最大层间位移角下,阻尼器失效结构所对应的地震动强度Sa(T1,5%)要更低一些,且这一现象在结构达到极限倒塌状态(平台段)时尤为明显。例如,在16%、50%、84%分位数曲线平台段,原结构Sa(T1,5%)分别达到5.1g,3.4g和1.9g,阻尼器失效结构分别达到4.1g,2.6g和1.4g。相比之下,阻尼器失效结构所承担的极限地震动强度分别降低了19.6%,23.5%和26.3%。此外,从加载至倒塌的全过程来看,虽然原结构与阻尼器失效结构在曲线的初始弹性段并无明显差别,但阻尼器失效结构会更快地达到其极限倒塌状态。例如,在50%分位数曲线中,两种结构在达到各自极限倒塌状态时,原结构的最大层间位移角为0.042,而阻尼器失效结构只有0.036。即自弹性阶段后,阻尼器失效结构会更快达到其极限承载强度,结构延性有所降低。由此可见,在极限情况下,阻尼器失效不仅会明显地将结构的极限承载强度降低约20%,还会降低结构延性,使结构自弹性阶段后更快达到极限倒塌状态。

3.3 损伤状态的参数定义

为了对结构进行性能评估,必须定义结构达到各种性能水准等级的临界值[13]。FEMA356定义了结构的4个不同性能水准等级,与之相应地,HAZUS[14]根据结构类型,对不同性能水准等级下结构最大层间位移角的数值提出了建议值,用来判定结构的不同损伤状态。根据HAZUS对结构类型的分类标准,本文算例的结构类型为C2H,其对应的4个不同性能水准等级的最大层间位移角临界值见表3。

表3损伤状态定义

Table 3 Definition of damage state

3.4 地震易损性分析

结构的易损性反映出在一定强度的地震动作用下,结构响应达到或超过某种性能水准等级的概率值。在本文中,IM代表输入地震动强度,DM代表结构在该地震动下的响应值θTds代表性能水准等级临界值,则结构的易损性可以表示为:

F(IM=x)=P[DM>θTds|IM=x]

(1)

由于结构的响应概率函数可用对数正态分布表示:

DM=Lognorm(θD,βD)

(2)

同理,结构的破坏状态界限概率也可以用对数正态分布来表示:

Tds=Lognorm(θTds,βTds)

(3)

则结构响应超过破坏状态界限θTds的概率为:

F(IM=x)=P[DM>Tds|IM=x]=

(4)

将原结构和阻尼器失效结构的IDA数据进行对数线性回归分析,如图5所示。可得出关系式:

ln[Sa(T1,5%)]=αln(θD)+b

(5)

其中,对于原结构,a为0.97604,b为4.3294;对于阻尼器失效结构,a为0.900 4,b为3.902 1。原结构的斜率a和截距b均大于阻尼器失效结构,意味着相同横坐标值下,原结构所能承担的地震动强度即纵坐标值Sa(T1,5%)要大于阻尼器失效结构,与前文分位数曲线处理后得出的结论一致。

图6中实线代表原结构,虚线代表阻尼器失效结构。可以看出,在正常使用的性能水准等级下,结构处于弹性状态,阻尼器还未开始屈服耗能,原结构与阻尼器失效结构的损伤概率几乎没有差别。而在其他三个不同性能水准等级下,相比于原结构而言,阻尼器失效结构的损伤概率均有所增加。结构的状态越趋向接近倒塌,其损伤概率增加越明显。而在接近倒塌状态下,阻尼器失效结构的易损性曲线的斜率始终大于原结构,意味着随着地震动强度的增加,阻尼器失效结构的倒塌概率增长的越来越快。其中,在Sa(T1,5%)为3g时增长约9%。

图5 IDA数据的对数线性回归Fig.5 Log-linear regression of the IDA data

注:实线代表原结构,虚线代表阻尼器失效结构。

在远超设防烈度的强震等极端荷载作用下,通常结构变形已经很大,结构本身更可能面临接近倒塌的状态。因此,在极端荷载作用下,阻尼器失效将增长结构的损伤概率,且随着地震动强度的增加,会加速结构倒塌概率的增长。

4 结 论

消能减震结构成功地广泛应用于抗震控制中,是基于性能设计方法的重要环节。然而在近年来某些极端灾害的调查中发现,消能减震元件自身发生了损伤甚至失效,警示了我们减震系统也存有潜在的隐患。因此,在极端荷载下,基于性能的设计方法值得进一步完善,需要考虑消能减震元件的失效及其对结构整体性能的影响。本文通过基于IDA方法的地震易损性理论,对某高层结构算例进行计算分析,对比发现阻尼器失效不仅会明显地降低结构所能承载的极限地震动强度约20%,还会降低结构延性,使结构自弹性阶段后更快达到极限倒塌状态;并且,阻尼器失效将增加结构的损伤概率,且随着地震动强度的增加,将加速结构倒塌概率的增长,对结构的整体性能产生了负面影响。因此,消能减震元件失效对结构极限性能的影响值得进一步的研究。此外,消能减震元件自身的损伤后性能及失效模式还有待系统的试验和研究。

[1] 吕西林,蒋欢军.复杂高层建筑抗震与消能减震研究进展[J].建筑结构学报,2010,31(6):52-61.

Lü Xilin,Jiang Huanjun.Research progress of earthquake resistance and energy dissipation of complex tall buildings[J].Journal of Building Structures,2010,31(6):52-61.(in Chinese)

[2] 吕西林,陈云,蒋欢军.新型可更换连梁研究进展[J].地震工程与工程振动,2013,33(1):8-15.

Lü Xilin,Chen Yun,Jiang Huanjun.Research progress in new replaceable coupling beams[J].Journal of Earthquake Engineering and Engineering Vibration,2013,33(1):8-15.(in Chinese)

[3] 中日联合考察团,周福霖,崔鸿超,等.东日本大地震灾害考察报告[J].建筑结构,2012,42(4):1-20.

Shigetaka ABE,Zhou Fulin,Cui Hongchao,et al.Inspection report of the disaster of the East Japan earthquake by Sino-Japanese joint mission[J].Building Structure,2012(4):1-20.(in Chinese)

[4] 谢丽宇,郝霖霏,张瑞甫,等.3·11大地震中减隔震装置的破坏及性能探讨[J].结构工程师,2015,31(2):10-20.

Xie Liyu,Hao Linfei,Zhang Ruifu,et al.Performance of seismic energy dissipation structure in the Great East Japan Earthquake[J].Structural Engineers.2015,31(2):10-20.(in Chinese)

[5] 谢丽宇,唐和生,薛松涛,等.首例油阻尼器破坏对结构设计的经验教训——日本3·11地震的启示[J].结构工程师,2015,31(2):2-9.

Xie Liyu,Tang Hesheng,Xue Songtao,et al.Lessons learned for design of passively-controlled structures from the Great East Japan Earthquake[J].Structural Engineers,2015,31(2):2-9.(in Chinese)

[6] 谢丽宇,唐和生,薛松涛.减振高层建筑的极限破坏及性能再生的研究现状及前景[J].结构工程师,2014,30(3):205-212.

Xie Liyu,Tang Hesheng,Xue Songtao.State-of-the- art and future trend in limit state and rehabilitation of vibration-controlled high-rise buildings[J].Structural Engineers,2014(3):205-212.(in Chinese)

[7] 邓付元,王涛,施唯.带阻尼器消能连梁抗震性能试验研究[J].土木工程学报,2016,49(S1):96-100+113.

Deng Fuyuan,Wang Tao,Shi Wei.Cyclic test on seismic behaviorof energy-dissipative coupling beams with dampers.[J] China Civil Engineering Journal,2016,49(S1):96-100+113.(in Chinese)

[8] 韩建平,吕西林,李慧.基于性能的地震工程研究的新进展及对结构非线性分析的要求[J].地震工程与工程振动,2007,27(4):15-23.

Han Jianping,Lü Xilin,Li Hui.State-of-the-art of performance-based earthquake engineering and need for structural nonlinear analysis[J].Journal of Earthquake Engineering and Engineering Vibration,2007,27(4):15-23.(in Chinese)

[9] Vamvatsikos D,Cornell C A.Applied incremental dynamic analysis[J].Earthquake Spectra,2004,20(2):523-553.

[10] Vamvatsikos D,Fragiadakis M.Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty[J].Earthquake Engineering and Structural Dynamics,2010,39(2):141-163.

[11] 熊谷仁志.RC 立体耐震壁および境界梁ダンパーを用いた超高層建物の地震応答[R].清水建設研究報告,2010.

Hitoshi Kumagai.Earthquake response of a high-rise building with reinforced concrete shear walls and coupling beam dampers [R].Shimizu Corporation Report,2010.(in Japanese)

[12] 吕西林.复杂高层建筑结构抗震理论与应用[M].北京:科学出版社,2015.

Lü Xilin.Seismic theory and application of complex high-rise structures[M].Beijing:Science Press,2015.(in Chinese)

[13] 武大洋.近场地震作用下轻型自复位消能摇摆刚架减震性能分析[D].兰州:兰州理工大学,2013.

Wu Dayang.Seismic mitigation of an innovative light energy dissipative rocking frame under near-field ground motions.[D].Lanzhou:Lanzhou University of Technology,2013.(in Chinese)

[14] Federal Emergency Management Agency.Advanced engineering building module[M].(AEBM) Technical and User’s Manual,2012.