“做数学”
———让课堂充满生命的活力——《三角形三边的关系》教学与反思
李晓红
【教学内容】
人教版四年级下册第63页。
【教学过程】
一、创设情境,激趣引入
师:(课件出示课本第63页例3情境图)这是小明家到学校的路线图,请大家仔细观察,从小明家到学校有几条路?
生1:小明家→邮局→学校。
生2:小明家→学校。
生3:小明家→商店→学校。
师:在这几条路线中哪条最近?为什么?
生1:因为第1条和第3条路线拐弯了,所以中间这条最近。
生2:我在图中通过测量得出中间的这条路线最短。
教师小结:同学们结合自己的生活经验谈了自己的感受。走中间这条路最近,其实这还和我们这节课所学知识有关呢!
师:(课件演示)大家看,小明家直接到学校的这条路是三角形的一条边,而从小明家到邮局再到学校的这条路线是三角形两条边的和,从小明家到商店再到学校的这条路线也是三角形两条边的和,看来这奥秘还和三角形的边有关系。这节课就让我们一起来研究三角形三边的关系。
二、动手操作,探究新知
1.明确任务,动手操作。
师:通过前面的学习,我们知道了三角形是由三条线段围成的图形,那是不是任意的三条线段都能围成三角形呢?下面我们来做个实验。
师:刚才老师给你们每一组都放了一个信封,里面有5根小棒,长度分别是4厘米、4厘米、6厘米、10厘米、12厘米,现在请同学们通过小组合作,从中选择三根小棒作为三角形的三边,用它们来围成三角形,并填好表格。
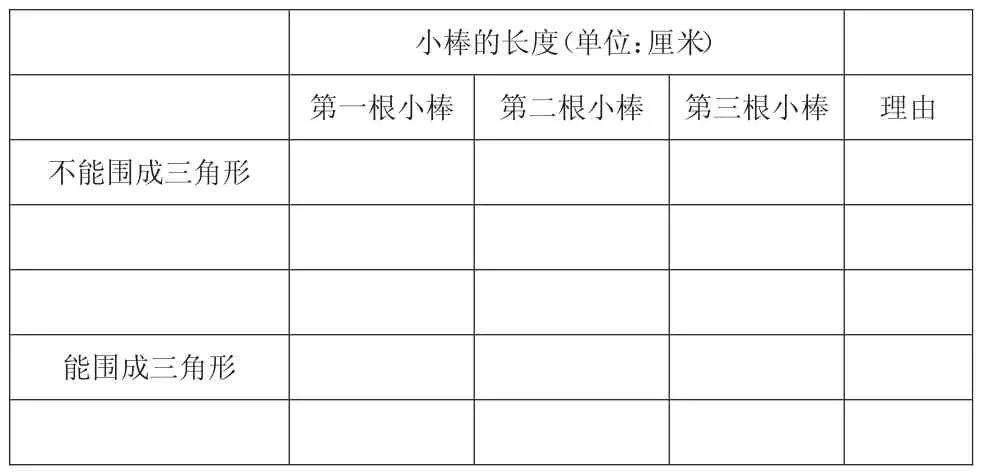
?
2.展示交流,提取数据。
师:哪一小组来说说哪三根小棒能围成三角形,哪三根不能围成三角形。其他小组认真听,看看你们的结论和他们的有什么不同?
教师根据学生的交流板书表格:
不能围成(4、4、10)(4、4、12)(4、6、10)(4、6、12)
能围成(4、4、6)(4、10、12)(6、10、12)
3.数形结合,探究结论。
师:通过刚才实验,我们发现并不是任意的三条线段都能围成三角形。那么请大家想一想:什么样的三条线段能围成三角形?什么样的三条线段不能围成三角形?
(1)研讨三条线段不能围成三角形的原因。
小组同学研究,学生汇报。
课件演示(4、6、12)不能围成三角形的动态过程。
(2)研讨三条线段能围成三角形的原因。
小组讨论,学生汇报。
课件演示(4、10、12)能围成三角形的动态过程。
(3)归纳结论。
师:请大家想一想:在围成的三角形中,三条边之间有什么关系呢?
生:我们发现两条边的和大于第三条边就能围成三角形。如4+10>12,这样就能围成三角形。
师:谁有不同发现?
生:我们认为必须每两条边相加,和大于第三条边才能围成三角形。比如 4+10>12、4+12>10、12+10>4。
师:哪些组还有不同发现?
生:我们认为最短的两边的和大于第三条边就能围成三角形。如只要4+10>12就能围成三角形。
师:还有吗?
生:如果只考虑一种情况是不行的,有时两条线段的和大于第三条线段,也不能围成三角形。
师:举个例子呢?
(引导学生引用“不能”的情况来反证)
生:比如在刚才不能围成的情况中:4+6<12、6+12>4、4+12>6,出现了两个大于的情况,但只要存在两边和小于(等于)第三边的情况,也不能围成三角形。所以只考虑一种情况是不行的。
师:那么为什么最短的两条线段的和大于最长的线段就能围成三角形呢?
生:因为最短的两条线段的和大于最长的线段,那么另外两组边加起来肯定比另一组长。如4+10>12,那么 4+12 肯定>10,12+10 肯定>4。
教师小结:因为只要最短两边的和大于了最长的边,那么其他任意两边的和都会大于第三条边。
4.验证结论。
师:刚才我们一直在讨论怎么样的三条线段能围成三角形,那么是不是每个三角形的任意两边之和都大于第三边呢?
(学生书本上找一个三角形,测量验证任意两边之和大于第三边)
师:你能用自己的话来说说“三角形任意两边之和大于第三边”是什么意思吗?
师:同学们现在能说说小明家到学校为什么走中间那条路最近吗?(学生说说)
三、深化认知,拓展应用
1.判一判:下面哪组的小棒能围成一个三角形?(单位:厘米)
(1)3、4、5(2)2、2、6(3)2、3、5
2.算一算:李老师要取三根小棒(整厘米数)围成一个三角形。我已经取了两根,第一根长4厘米,第二根长7厘米。第三根取几厘米,就一定能围成一个三角形?(第三根小棒的取值范围大于3小于11)
3.做一做:有两根长度分别为2cm和5cm的木棒。
(1)用长度为3cm的木棒与它们能摆成三角形吗?为什么?
(2)用长度为1cm的木棒与它们能摆成三角形吗?为什么?
(3)要能摆成三角形,第三边能用的木棒的长度范围是多少?
四、课堂小结,反思评价
师:通过这节课的学习,你有哪些收获?关于三角形三边关系还有值得我们探索的地方,比如三角形任意两边的差与第三边有怎样的关系?有兴趣的同学课外可以自己进行探索。
【教学反思】
一、“做数学”,要从数学与生活的联系入手
学生对于三角形三边关系的认识并不是一片空白,他们对三角形两边的和大于第三边有一定的生活经验和感性认识。因此,我寻找知识在生活中的数学原型,创设了这样的数学情境:小明去学校怎样走最近,为什么?这样的问题情境贴近学生的生活,使得对于三角形三边关系的探索内化成学生的一种需要。
二、“做数学”,要在“做”字上狠下功夫
让学生采用操作实践、自主探索、大胆猜测、合作交流、积极思考等活动方式学习数学,是“做数学”的关键。我为每个小组准备五根4cm、4cm、6cm、10cm、12cm的小棒,让学生尝试组合。在围的过程中,学生会出现能围成和不能围成两种情况。我抓住这一契机巧妙设疑:为什么同样是三段小棒有的能围成一个三角形,有的不能够围成一个三角形呢?学生在经历围的过程中直观发现,两根小棒长度之和小于或等于第三根小棒时,不能摆成三角形,只有大于第三根小棒时,才能摆成三角形,得出了三角形两边之和大于第三边的结论,从而初步认识了三角形三边的关系。教师提问“谁有不同的发现?”这使学生敏感地意识到这种表达可能有问题,问题出在哪呢?学生不得不深思。最后学生终于发现:三角形任意两边之和大于第三边。对“任意”二字的理解,使学生对三角形三边之间关系的认识得到了深化。

