凸显思维过程 开发智力潜能
——《新思维儿童数学》(1A)实践感悟
王国宏 俞 波

优质的教材是培养优秀人才所使用的材料,是实现教学目标的载体。2017年,中国科学院心理研究所特邀研究员、浙江省功勋教师张天孝先生悉心编著并推出了《新思维儿童数学》系列读本。从2017年9月开始,杭州地区进行了首轮实践和实验。我们有幸成为研究团队的成员,在进行了一个学期的实践和研讨后,深刻体会到1A册读本灵活、多样、独特、关联的编写特点,是现行各种版本教材内容很好的补充和数学教师进行数学思维训练的范本,能有效地提升学生的数学素养。
一、创新基础,有利于学生学会学习、学会思考
1A册第三单元中,张老师安排了一节特别的概念课——《翻倍与折半》,这是其他教材没有的内容。我们在请教新思维教研团队后了解到翻倍与折半是解决很多典型数学问题的重要基础,如“和差问题”:两个数的和是a,差是 b,求较大数,就是(a+b)折半,求较小数,就是(a-b)折半;又如“差值等分”问题:大筐有12个梨,小筐有4个梨,从大筐里拿出几个放到小筐,两筐梨一样多?需要将两筐梨的相差数折半;……
这样的教学内容学生能不能学会呢?我们仔细推敲材料,发现张老师的设计实在是太巧妙了,他以多元表征的方式呈现翻倍与折半的内涵,非常有利于学生获得概念。
“图像”表征翻倍与折半:
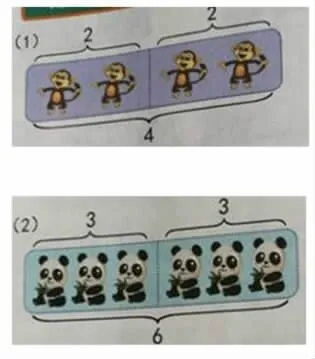

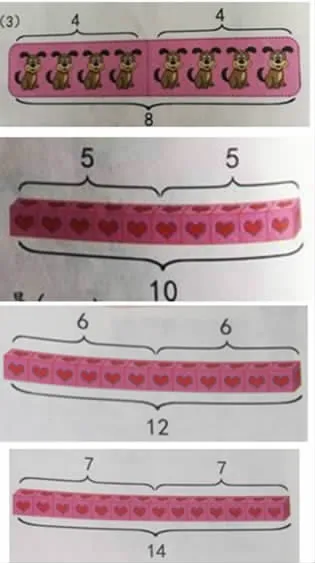
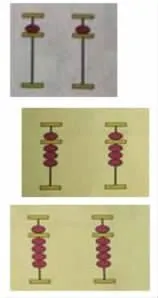


“数形结合”表征翻倍与折半:

“语言”表征翻倍与折半:
20是( )的翻倍;20折半是( )。5是( )的折半;5翻倍是10。
笔者对这节课进行了课堂实践,发现其内容、情境、序列都非常合理,教师教学时只要按照教材设计实时展开、适当调控,就能很自然地启发学生独立思考,逐步深入。当我们要求学生用一句话来总结本课的学习体会时,有的学生说:“老师,折半和翻倍是一对好兄弟,一元钱折半是五毛钱,五毛钱翻倍是一元钱。”有的学生说:“老师,我想让我们的绿色植物不断翻倍、变多,这样我们的环境就能越来越好了。”马上有个学生仿照说:“老师,我想让我们的困难不断的折半、减少,这样我们就会更加开心了!”学生的活学活用令人惊喜!
二、开放课堂,帮助学生体验成功、感受快乐
教材第二单元中《认识立体图形》一课,经我们与人教版的相关内容对比,浙教教材中更注重将各种立体图形与生活原型相联系,包括在具体物品中抽象出立体图形与基于立体图形发散想象具体物品。因此,在教学处理上,强调学生要结合自己已有的生活经验来理解、概括这些图形的特征。


《新思维儿童数学(1A)》
“立体图形”教材页面
王国宏老师执教了这节课,在说下课的时候,很多学生还不想下课,有一位学生站起来问王老师:“老师,我认为你说的圆柱体站着时可以叫圆柱体,如果平放在桌面上,我想叫它‘圆滚体’,您认为可以吗?”王老师追问:“你为什么想叫它圆滚体呢?”这位小女孩大胆地说出了自己的想法,她说:“通过刚才的玩一玩,我看到这五种立体形状的物品平放在桌子上,球是向四面八方滚动的,而圆锥体是围绕一个点滚动的,只有圆柱体是向一个方向滚动的,我觉得叫圆滚体让我一下子想到了它特别的地方。”王老师马上表扬这位说出这些图形在滚动时不同特征的学生,又引导学生想象:“如果老师从下往上,水平地去切这些图形,切得的平面图形有什么变化?”学生总结得出:从下往上每个截面都一样的,叫柱体;越切越小,直到一个点的,叫锥体。王老师问:“现在,你们觉得圆柱体和圆滚体哪个名字更好呢?”刚才提问的同学自己站起来说:“原来“柱体”和“锥体”也有特别的意思。我们还是叫它圆柱体吧!”
这个案例使我们深刻理解到有意义的学习是解放学生的学习,有意义的课堂是开放的课堂。在这样的课堂里,学生有机会用自己的方式去了解、理解各种概念、规则,可以安全、自如地表达自己的思考、见解,体会到自主学习的权利和成功的快乐,心悦诚服于逻辑、道理。
三、不求易、不避难,培养数学学习的良好品格
第一单元中《几加几》一课内容独特,难度系数不小。根据教材,杭州市贺知章小学的许老师是这样展开教学的。
(一)探究等式
1. 感知“=”的含义。
(1)列一列。
请你找一找1~9这些数中哪两个数相加和是9?
根据学生发言,形成板书:
4+5=9 3+6=9
2+7=9 1+8=9

(2)找一找。
引导学生观察四个加法算式,发现排列规律。
看算式:第一个加数一个一个减少,第二个加数一个一个增加。
看图像:左右对称,大数配小数。
2.构建等式。
4+5=3+6 4+5=2+7
4+5=1+8 3+6=2+7
3+6=1+8 2+7=1+8
(二)自主探究
1.请你写出两个数相加和是7的算式,看谁写得又对又好。
2. 从 1、2、3、4、5 中选四个数,使两两相加的和相等。
当时许老师班里共有42名学生,其中35名是外来务工人员子女,应该说学生基础比较薄弱,但课后测试显示,班级正确率高达93%。
经过对执教教师、受教学生的访谈我们豁然开朗。这个内容本身确实有一定的难度,但是依照张天孝老师的《新思维儿童数学》序列化地训练之后,学生在思考的系统性和灵活性上有了很大的变化,充分体现出对关系的关注、规律的敏感、数形结合的认知方式、有序地思考等等。同时,学生更乐于接受有一定难度的问题挑战,更能沉下心来长时间思考、作业,不求易、不避难,有着良好的意志品格。
学者成尚荣指出:当下的教育在不知不觉中小心翼翼地为自己画了一个圈、筑了一堵墙,这个圈、这堵墙的名字叫做现实性,教育只关注学生的现实性且时时紧盯着学生的现实性,始终没有勇气探出头来看看墙外有没有更广阔的天地和更美丽的风景,这个墙外的风景和天地正是学生的可能性。
《新思维儿童数学》(1A)就为学生的数学学习提供了很多的可能性。全书着眼于高层次思维的培养,体系缜密、题例丰富、思想方法循序渐进、螺旋上升,如果能够系统使用,发展学生数学思维的效果是十分显著的。当然,我们一线教师也可以配合自己的教学进度有选择地使用,以达到拓展学生思维的功效。

