提前干预错例 提高解题效率
孟建军

学生在学习过程中出现错误都会有一定的原因,我们能否对该知识点有可能产生的思维误区进行预设呢?要想预设必须先分析错题形成的原因。
一、小学数学典型错题形成的原因
1.教师方面。
(1)缺乏提携。
当师生一起学习一个新的知识时,这些学习初期产生的各种信息在探索的过程中会逐渐清晰明朗起来。在这个过程中,教师的讲解就起到提纲挈领的作用,能很好地帮助学生进行抽象概括。如果缺乏教师的提携,会导致学生理解不清晰,影响他们的知识建构。
例如:判断在同一时间同一地点树高与影长成什么比例。在书本和作业本的练习中,都是以表格形式提供相关数据,通过计算相对应数的比值后再进行判断,错误率几乎没有。但在综合练习中只以文字形式呈现“在同一时间同一地点树高与影长成什么比例?”就出现了16名学生判断不成比例,2名学生判断成反比例。学生的理由是“题目中没有出现什么一定”。
通过反思可以知道书本及作业本练习仅仅是从数据结果进行了判断,并没有真正理解其中的含义。如果在练习中引导学生思考比值表示什么其实是什么一定?为什么要强调同一时间同一地点?并作一概括,就会促进学生的思考,让他们真正理解正比例的意义。
(2)缺乏耐心。
学生理解知识需要过程,当学习了一个新知后必定要通过一定的训练才能达到熟练与完善。当学生还不理解新知时,进行再多的训练也是事倍功半;当学生对新知有一定的理解时,如果不进行不同层次的训练,理解还只是认知层面,就不能很好地综合应用。特别是对学困生,他们的理解、接受过程相对要长一点、慢一点。“心急吃不了热豆腐”,在学习上也同样适用。虽说学习了教学内容,但学生还没理解透彻、没内化,认知还不完善,对后续学习极易产生干扰。
(3)缺乏指导。
当某一知识点练习出现错误,如果不进行正确的、及时的指导,让错误的认识继续下去,很容易一错再错,难以改正。
例如:“一个长方形的周长是30厘米,它的长和宽的比是3∶2,长和宽分别是多少厘米?”学生初次解决此题时有60%的学生直接把30按3∶2分配,得到长和宽分别是18厘米和12厘米。
【思考:为什么有这么高的错误率?原因就是教师在解决按比例分配内容的时候,没有将按比例分配问题解决到位,教师都是按教材来新授按比例分配问题,以至于出现总数与比没有对应。可以通过实践活动、验证或图示方法来找到比与哪一个总数相对应。】
(4)缺乏情感沟通。
没有丝毫兴趣的强制性学习,将会扼杀学生探索真理的欲望。一些教师对探索性问题把握程度不够,教学中创设的问题不是过于简单,就是过于难。对探索性要求,一方面所给过于简单,缺乏思考余地;另一方面,所给的数学问题过于复杂、高深,超出了学生数学认知结构的“最近发展区”,使学生由于对问题解决困难而产生厌烦心理。
2.学生方面。
(1)概念题一知半解。
如果让学生单独求圆的周长和面积,大多数学生都没有问题,看上去好像周长和面积的知识掌握得比较好。可遇到求半圆的周长和面积时,错误百出。例如:
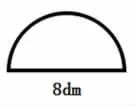
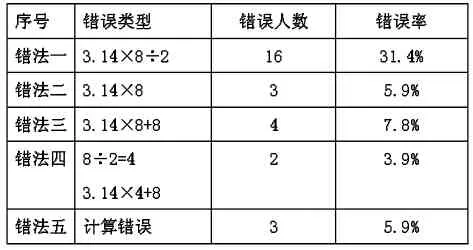
测试后对学生周长计算的错误进行了罗列和统计如下:
?
【思考:为什么很多学生会出现这样的问题呢?我想其中的主要原因是学生的空间观念弱,对周长的意义理解不到位,没有从图形外围一周的长度这个角度理解周长的含义。只是停留在两个图形之间的关系的角度解决问题。而且对周长和面积计算方法不够熟练。】
(2)计算题一错再错。
计算是小学数学内容的重要组成部分,是数学学习的基础。新课程虽删除了一些比较繁琐的计算题,降低了计算难度,然而学生的计算错误仍然困扰着大家,常常碰到一些简单的题目都不能正确计算。我们习惯把错误归咎为学生“粗心大意”所致。
例如:计算 25×4÷25×4 时,部分学生不假思索地算成25×4÷25×4=100÷100=1。
【思考:看似一道简单的题目,为什么错误率这么高呢?我想25×4 是一个强信息,在“凑整”因素下,对学生产生了强烈的刺激,使他们在计算时忽略了运算顺序、计算法则,采用简便计算导致错误。】
(3)综合题一头雾水。
教师经常遇到学生对新学内容很快理解,并对模仿性的练习做得很好,但是在做综合练习时,就会出现不同程度错误的现象,这种现象反映了学生对知识的理解是一知半解。
【思考:如果把分数改成整数或小数,那么上述做法就不会出现,为什么改成分数以后学生会出现这类问题呢?通过与学生的谈话了解到:他们认为求还剩百分之几,就用以前的方法“剩下=总数-用去,再将答案化成百分数”,没想过有单位的数量是不能化做百分数的,因为百分数是分率,自己把数量与分率混淆了。应该用“还剩的重量÷总重量×100%=剩下百分之几”。】
(4)思考题一见就避。
思考题是常常被学生忽视和被教师轻视的题目,学生自己觉得思考题肯定做不出来的,即使教师讲了也不一定能理解,长此以往,学生看见思考题和星号题往往熟视无睹,连动脑筋的欲望都没有了。
【思考:这道题错误率高的原因是它的单位“1”是隐含和变化的。学生往往把题中的单位“1”当作相同的全班人数,并没有真正理解这两个单位“1”表示的全班人数其实是不一样。的单位“1”是原来的全班人数的单位“1”是现在的全班人数。单位“1”发生了变化,现在的班级人数比原来的班级人数多10人,所以和是两个单位“1”不同的分率,只有找到没有变的量,才是解决问题的关键。】
二、小学数学典型错题的提前干预策略
1.教学方法求新。
(1)为理解而教。
一节课的内容既要考虑到每位学生的可接受程度,又要考虑到这节课的重难点。如果教学内容比较难,我们就有必要降低难度,即分散难点,让绝大多数的学生都能够接受。
例如:
题目一:在分率语句中找出单位“1”,并列出数量关系式。
题目二:看图列出算式。
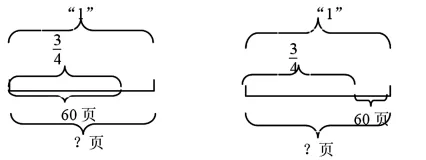
通过这样的专项训练,帮助学生理解单位“1”的量,找准对应量与对应分率之间的对应关系这一难点。既突破教学重难点,又增加了练习密度,降低了分数除法应用题的难度,使学生在解决分数应用题时减少错误的发生。
(2)开发错题资源。
“错误”是师生在认知过程中发生的偏差与失误,它伴随教学的始终,是无法避免的。我们应冷静地分析错误原由,有效地挖掘错误中蕴含的创新因素,错题也是有效教学的一种再生资源。
在长方形中剪圆,很多学生认为用长方形面积÷圆面积,就可以得到几个圆。教师可以设置这一“陷阱”,甚至诱导学生“犯错”,再引导学生自已从错误的迷茫中走出来,使学生经历一个从错误认识走向正确认识的过程,从而提高学生的反思能力,唤醒学生的质疑精神和探究欲望。
例如:“一块长方形铁皮,长是 6厘米,宽是4厘米,如果用它剪半径1厘米的圆片,最多可以剪多少个?”学生根据以往的经验,往往会用大面积去除以每块的小面积,即 6×4÷(3.14×12)≈7(个)。
我首先让学生通过在草稿本上画图来验证是不是7个,然后再引导学生思考为什么会造成这种情况?接着让学生结合自己画的图探讨计算方法。最后学生找到了正确的解法是(6÷2)×(4÷2)=6(个),归纳出解题方法:圆片的数量=沿长剪几个直径×沿宽剪几排直径。让学生在实践中体会原来解法的错误,让学生在摔打中学会对数学问题作深入思考。
2.指导解题技巧。
(1)培养学生正确审题。
①圈一圈。
许多学生审题不着要领的原因就是没有注意到题目中的关键性字词。这是因为小学生在观察时只注意了整体,没有注意细小的地方,因此看错了题目,造成了感知的错误,列出错误的式子,最终答错。
②画一画。
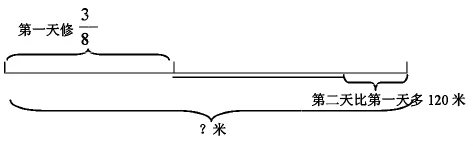
图的力量比文字更简洁有力,分数应用题如果能根据题意画成线段图,借助线段图就可以把握数量关系。
让学生找出分率语句,找出单位“1”,判断出方法,再画出线段图。看图只要找到120米的对应分率,就可以求单位“1”的量。
③列一列。
一些条件复杂、纷乱的题目,将所给条件和所求问题摘录下来,通过条件归纳整理成两种数量,说说这两种数量之间的关系,来判断什么比例关系。
例如:一个工人要制造一批机器,原计划每天制造20台,30天完成。可实际15天就完成了计划,实际每天制造多少台?(用比例解)
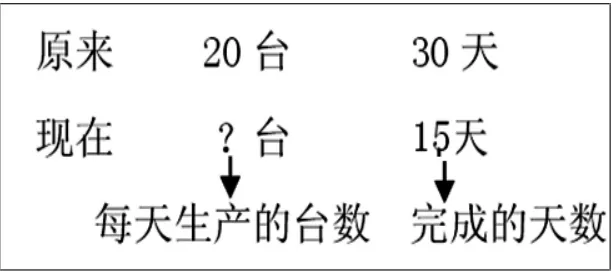
审题能力反映了一个人的思维能力,是数学素质的具体体现。审题能力的培养不是一朝一夕就能见效的,必须贯穿于整个数学教学的始终,要有计划、有意识地运用科学的方法进行长期的渗透,使学生不断地受到启迪,在潜移默化中,逐步领悟,以提高思维能力。
(2)师生个人典型错题本。
①学生易错本建立。
学生的成长过程中,都不可避免会做错题,若能把做错的题集中在一起,可以清晰地发现学生学习过程中的障碍,这样的“错题集”蕴藏着重要的启示功能。
②教师典型错题本建立。
每个学生之间虽然存在个体差异,错题可能不同,但有些题目容易出错,有些题目在班级中的错误率也比较高,这也是教师碰到的普遍问题。教师建立典型错题记录分析本也是非常有必要的。教师在每次批改作业时,可以将本班级学生中容易出错、错误率较高的题目记录在典型错题记录分析本中,把学生各种错题的解法记录下来,分析其出错的普遍原因,寻找问题的症结,然后在教学中进行教法的改进。
3.精练典型错题。
(1)对比练习,凸显不同。
通过对比性练习,增加学生的思辨能力,是提高思维深刻性的有效手段。学生会做类似的题还不能确定其是否真正掌握,如果在对比练习中都能分辨解决,说明思维并没有停留在机械识记上,学生在练习中通过一系列的分析、推理、判断等思维活动,对题目的情况、类别等方面进行辨别分析,已具有相当高的思维水平。
例如:刚学完分数除法应用题以后,学生解答题目的时候往往都会用除法来解答,使学生产生一定的思维定势。因此在解决分数乘除法练习时,我设计了一些有对比性的题目,让学生进行辨别、判断、分析。
(2)主题练习,凸显类同。
学生对某一个知识类型产生错误比较多,我们可以设计一个主题训练,进行每日一练,连续训练一两个星期,从而达到巩固的目的。
4.巧用现代媒体。
小学六年级学生的思维正处在由具体形象思维向抽象思维过渡的时期,这就构成了小学生思维的形象性与数学的抽象性之间的矛盾。如何解决这一矛盾?利用多媒体进行教学,能够成功地实现由形象思维向抽象思维的过渡。将比较抽象的知识更直观地、更形象地展示出来。
例如:通过课件演示,将长方体铁块等体积变形为上升的圆柱体,求圆柱体的高。把深奥的文字理解变为比较直观地图形理解。

