基于非线性分位数自回归的股市收益自相关性研究

康 宁 ，吴丽媛 ，荆 科

（阜阳师范学院 a.经济学院；b.数学与统计学院，安徽 阜阳 236037)

股票市场是金融市场的重要组成部分，股票收益的自相关性是金融市场研究的热点问题,对股票价格预测及股市风险度量具有重要意义。传统金融学观点认为股票收益不存在相关性，因此股票收益是不可预测的。Fama在有效市场假说中指出，一个健全有效的股票市场中，股票价格服从随机游走，能够完全反映可得信息，从而历史收益和未来收益不相关，市场中不存在超额收益[1]。然而随着计量技术的发展，大量的理论和实证研究表明多数国家的股市收益存在相关性，并对其背后隐含的经济机理进行分析。例如，Tversky等指出，如果股票收益存在正自相关性，表明价格对新信息存在反应不足，存在“动量效应”，反之若股票收益负自相关，则表明价格对新信息存在反应过度，存在“反转效应”[2]。Bondt等表明当股价系统性反应过度时，意味着违反弱式市场有效性，仅仅依靠过去收益就可以预测出未来的反转[3]。Campbell等研究了单只股票指数的交易量和日收益率的关系，通过控制交易量，发现股票收益率存在负自相关[4]。Lewellen选择CRSP数据库中1941到1999年若干股票月度数据，发现股票收益序列具有负自相关性，但大部分情形在统计意义上不显著[5]。田诗成等以上证综指为代表，研究了股市收益波动的非对称行为和持续性行为[6]。李云红等发现中国股市的有效性存在时变特征，并且市场环境对风险溢价的作用不明显，但对股市收益预测具有显著影响[7]。

然而，上述工作都是在均值框架下建立线性模型，研究股市收益的自相关性。由于金融市场及经济规律的异质性，线性的均值模型往往难以具有代表性，其原因在于，第一，均值回归仅能揭示历史收益对未来收益的条件均值是否存在显著影响。现实生活中，收益序列通常存在尖峰厚尾的特征，单纯的均值回归往往难以刻画收益序列的整个条件分布尤其是尾部分布特征；第二，线性模型存在一个前提假设，即不论前期收益是正向还是负向，对当期收益的冲击都是相同的。然而，这种同质性假定往往并不符合实际。国内已有文献证实中国股市存在非线性的异质特征，例如严太华等使用马尔科夫转换模型分析上证综指周收益率，结果表明序列既是非线性时间序列又有结构性变化[8]。朱慧明等发现中国股市投资者存在典型的羊群效应，并且政策机制对不同行业的收益和交易量相关性存在异质性作用[9]。许启发等研究表明网络情绪波动对股市收益在一些特定分位点区间存在显著因果关系影响，从而为特定条件下股市收益的预测提供了依据[10]。

目前，国内少有文献将非线性机制与分位数回归理论相结合来研究中国股市收益序列的自相关性。鉴于此，本文在分位数回归框架下，以正负向收益作为分段机制，建立非线性分位数自回归模型，用以刻画收益序列的自相关特征。其优势和依据在于：第一，Koenker等提出的分位数回归方法能够全面刻画条件收益的整个分布信息，尤其是充分反映分布的尾部特征[11]。Baur等使用Koenker等提出的线性分位数自回归模型[12]，研究了道琼斯指数收益率的自相关性，发现低分位点处收益序列正自相关，而高分位点与之相反[13]。这一结论为使用分位数回归方法来研究股市收益的异质性特征提供了参考性依据。第二，欧阳敏华指出金融市场上时间序列受到正负不同方向的冲击时，变化规律不同[14]。这一结论为使用正负向收益作为分段机制提供了依据，有助于更好的发现股市收益非线性动态变化特征。

本文实证选取上证综指日收益率、周收益率及月收益率数据，结果表明，不同时间频率的收益序列自相关特征具有一定的稳健性。具体表现为：第一，当前期收益为负向时，从低分位点到高分位点，收益序列由正自相关逐渐变为负自相关；当前期收益为正向时，结论与之相反。第二，受极端市场环境影响，收益序列在尾部分位点处的自相关性较强，在中位点处自相关性较弱。与传统的均值模型对比，本文结论能够全面刻画条件收益分布，充分反映收益序列的非线性动态变化特征，从而为股票价格预测及股市风险度量提供有益决策依据。

1 模型与方法

1.1 模型表示

假设时间序列为收益率序列，下面以前期收益的不同方向作为非线性机制，在整个分位区间上建立非线性分位数自回归模型，用以捕捉正负向收益对自相关特征的不同影响。考虑最简单情形，一阶形式的模型表述如下：

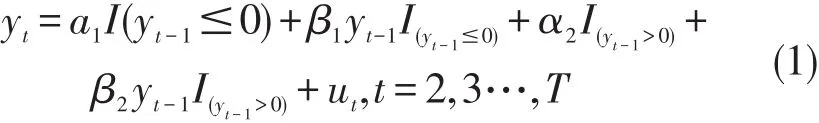
式中，I(·)为示性函数。I(yt-1≤0)等于 1 表示前期收益为负，I(yt-1＞0)等于1表示前期收益为正。

从而yt在历史收益条件下的τ分位数为：

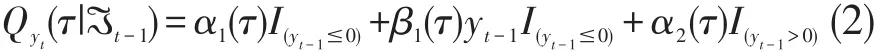
式中，ℑt-1为直到t-1时刻的信息集，τ(0＜τ＜1)为分位点。将回归参数表示为θ(τ)=(α1(τ),β(τ),α2(τ),β2(τ))，其中α1(τ)、β1(t)代表前期收益为负时的回归参数，α2(τ)、β2(t)代表前期收益为正时的回归参数，其取值在不同分位点处是可变的，呈现异质性。类似可推出该模型的高阶形式。

1.2 参数估计

记εt(τ)=yt-Qyt(t|ℑt-1) ， 目 标 函 数，根据 Koenker等提供的线性规划方法，通过优化下式来获取模型的参数估计[11]。

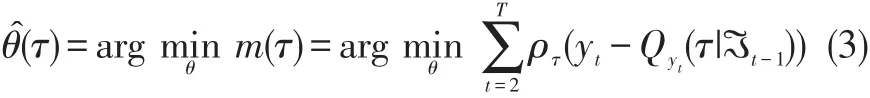
式中，ρτ(u)为分段线性函数，满足

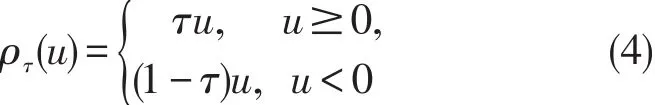
Koenker等证明，在大样本条件下，θ̂(τ)满足相合性与渐近正态性。

1.3 诊断检验

模型诊断检验包括，第一，非线性效应检验，即检验正负向收益的冲击是否存在同一性，采用Galvao等[16]单个分位点处的SupWald和AveWald检验统计量，以及整体分位点处Kolmogorov-Smirnov型的检验统计量。第二，回归方程及回归系数显著性检验，采用Koenker等构造的似然比检验[16]。

2 实证分析

2.1 数据选取及描述性统计分析

本文从锐思数据库选取上证指数日收益率、周收益率和月收益率作为研究对象，时间跨度为1990年12月19号到2017年7月16号，剔出节假日和非交易日，共有6 519个日数据，1 472个周数据，319个月数据。数据选取的特点在于：第一，上证综指市场影响力大，具有代表性；第二，时间跨度长，选取了1990年12月19日沪市开市以来的历史数据；第三，不同时间频率的数据有助于分析中国股市波动的稳健性。

表1给出收益序列的描述性统计分析结果，可以看出，三个收益序列的共同特征为：序列尖峰厚尾，JB检验均拒绝了正态分布的原假设，ADF检验拒绝单位根原假设，表明序列平稳。不同之处在于，随着时间频率的降低，收益序列的极差和标准差逐渐增大，偏度和峰度逐渐减小，从而说明序列的波动性随时间频率的减少不断增强，而尖峰厚尾特征逐渐减弱。

表1 描述性统计、正态性检验及平稳性检验

2.2 日收益序列的自相关性分析

建立非线性分位数自回归模型，用以捕捉正负向收益对自相关特征的非线性影响。选取0.01、0.05、0.1、0.5 及 0.9、0.95、0.99 七个代表性分位点，首先赋予分位点经济意义，这里中位点代表温和的市场环境，而尾部分位点代表极端市场环境，具体而言下尾部0.1、0.05、0.1分位点代表低迷的市场，而上尾部0.9、0.95、0.99代表积极的市场。

表2给出日收益序列的参数估计及诊断检验结果。图1给出日收益序列回归系数估计图，阴影区间及虚线分别为分位数回归下的回归系数估计值及95%置信区间，红色直线及红色虚线表示均值回归的估计值及95%置信区间。

从表2可以得到以下诊断检验结果。第一，非线性检验表明，日收益序列存在显著的非线性效应。不管是单个分位点处的Supwald检验，还是整体分位点处的K-S检验，检验的p值都为0.000，拒绝了线性原假设。第二，似然比检验表明，在所有分位点处回归方程和回归系数显著（5%水平）。均值模型结果与之类似。

表2及图1中参数估计结果显示，日收益序列存在典型的非线性特征。具体体现在：第一，当前期收益为负向时，随着分位点的增加，自相关系数呈下降趋势，取值由正转负，这表明从低分位点到高分位点，日收益序列由正自相关逐渐变为负自相关；而当前期收益为正向时，结论与之相反。第二，自相关强度依赖于分位点，其中尾部分位点处的自相关性较强，中位点处较弱。

下面从行为金融学视角，重点分析尾部分位点处（即极端市场环境下），日收益序列的自相关特征。以前期负向收益为例，可以看出：第一，0.01分位点和0.09分位点处自相关系数的绝对值较大，0.5分位点处最小，这表明日收益序列在极端市场环境下自相关性较强，容易导致市场异象，而在温和市场环境下的自相关性较弱，相对而言更符合有效市场理论。第二，低分位点处（0.01、0.05、0.1），日收益序列正自相关，即前期收益和当期收益同向变化，表明低迷的市场对负向收益反应不足，存在“动量效应”；而高分位点处（0.9、0.95、0.99），日收益序列负自相关，即前期收益对当期收益存在反向校正作用，表明积极的市场对负向收益反应过度，存在“反转效应”。类似可以分析前期收益为正向的情形，结论与之相反。

以上结论表明，正负向的前期收益对当期收益存在非线性影响，尤其在尾部分位点（即极端市场环境下），作用更加明显。显然，该结果与均值模型存在显著区别。均值模型仅能估计出均值水平下收益序列的弱自相关性,而分位数模型不仅能度量出日收益序列的非线性动态特征，更重要的是能够捕捉收益序列尾部分布的强自相关特征。

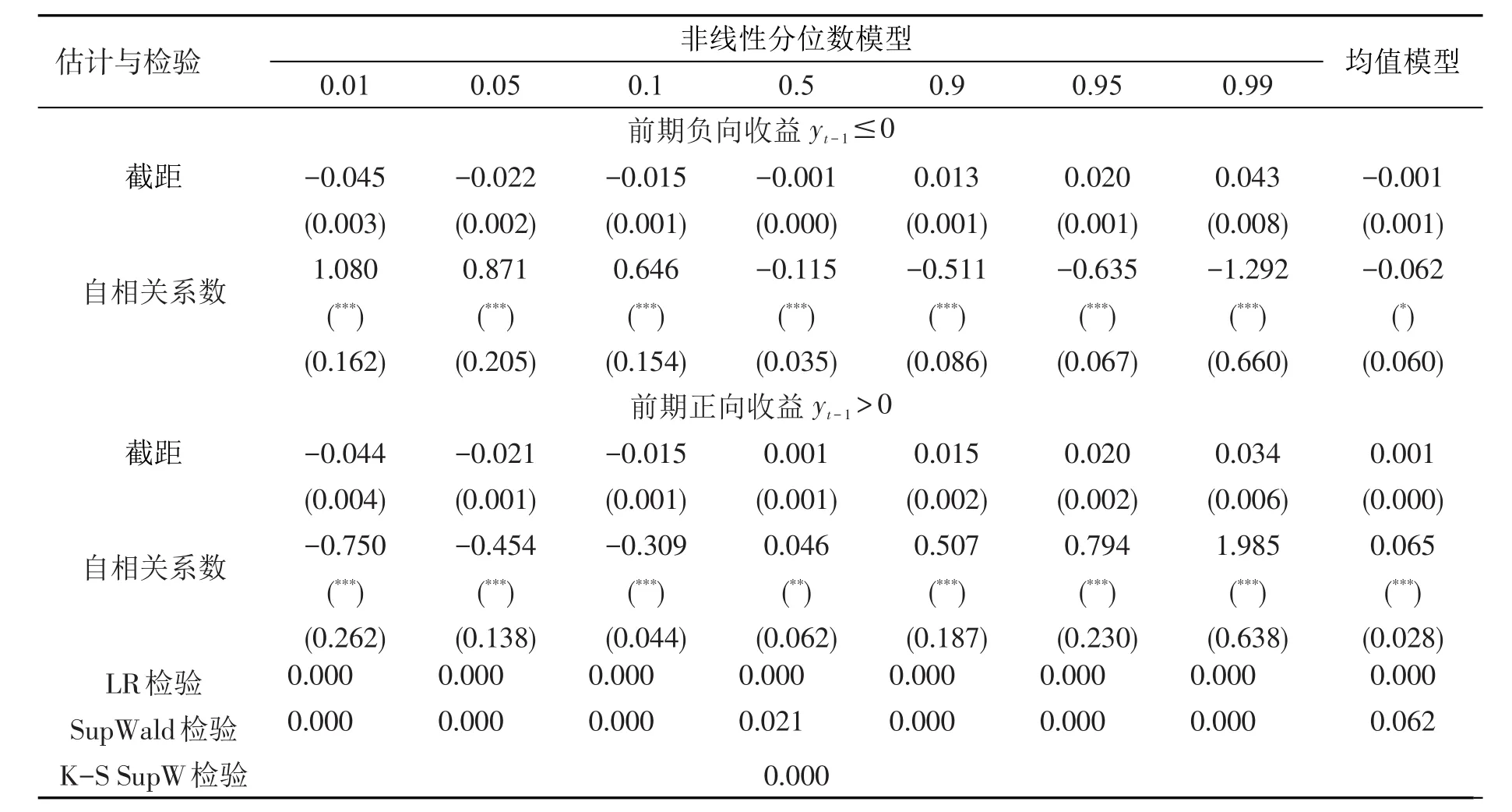
表2 日收益序列参数估计及诊断检验

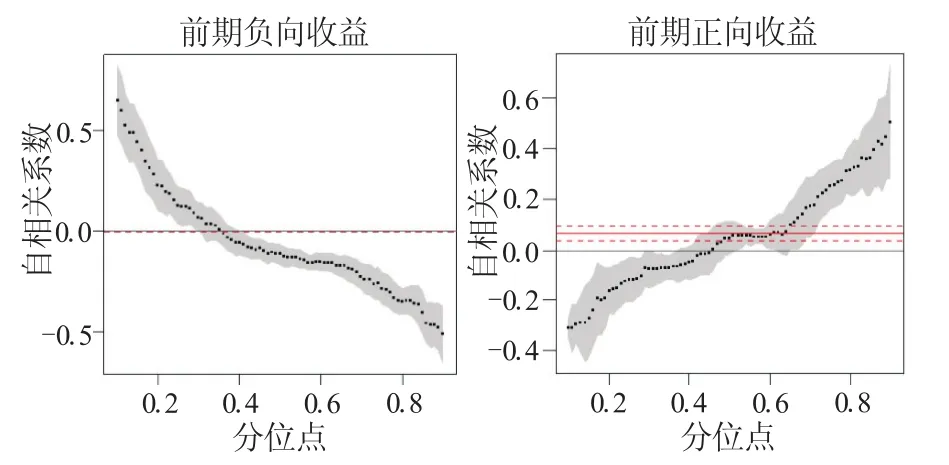
图1 日收益率的自相关系数估计图

2.3 周、月收益序列的自相关性分析

为考察在正负收益的影响下，不同时间频率的收益序列的自相关特征是否具有稳健性。表3和表4进一步给出周收益序列和月收益序列的参数估计及诊断检验结果。图2、图3分别给出周收益序列和月收益序列自相关系数估计图。可以从两方面对以上结果进行分析。

首先，诊断检验结果表明，不管是非线性检验，还是回归方程与回归系数的显著性检验，周收益序列和月收益序列的检验结果都与日收益序列类似。不同之处在于，在0.1和0.5分位点处，月收益序列的Supwald检验在1%水平下接受了线性原假设，似然比检验在1%水平下显示回归方程和回归系数不显著。

其次，参数估计结果表明，不同时间频率的收益序列的动态变化趋势较为一致，具有稳健性。具体表现为：第一，当前期收益为负向时，收益序列都呈现出低分位点处强正自相关，中位点处弱自相关，高分位点处强负自相关的特点；第二，当前期收益为正向时，在尾部分位点处（即极端市场环境下），不同时间频率的收益序列变化趋势稍有不同，其中日收益序列和周收益序列表现出一致的强自相关性，而月收益序列仅存在弱自相关性。

总体而言，以上结论能够证实，在正负向收益的影响下，股市中不同频率收益序列的自相关特征存在一定的稳健性：当前期收益为负向时，稳健性较强，而当前期收益为正向时，稳健性稍弱。

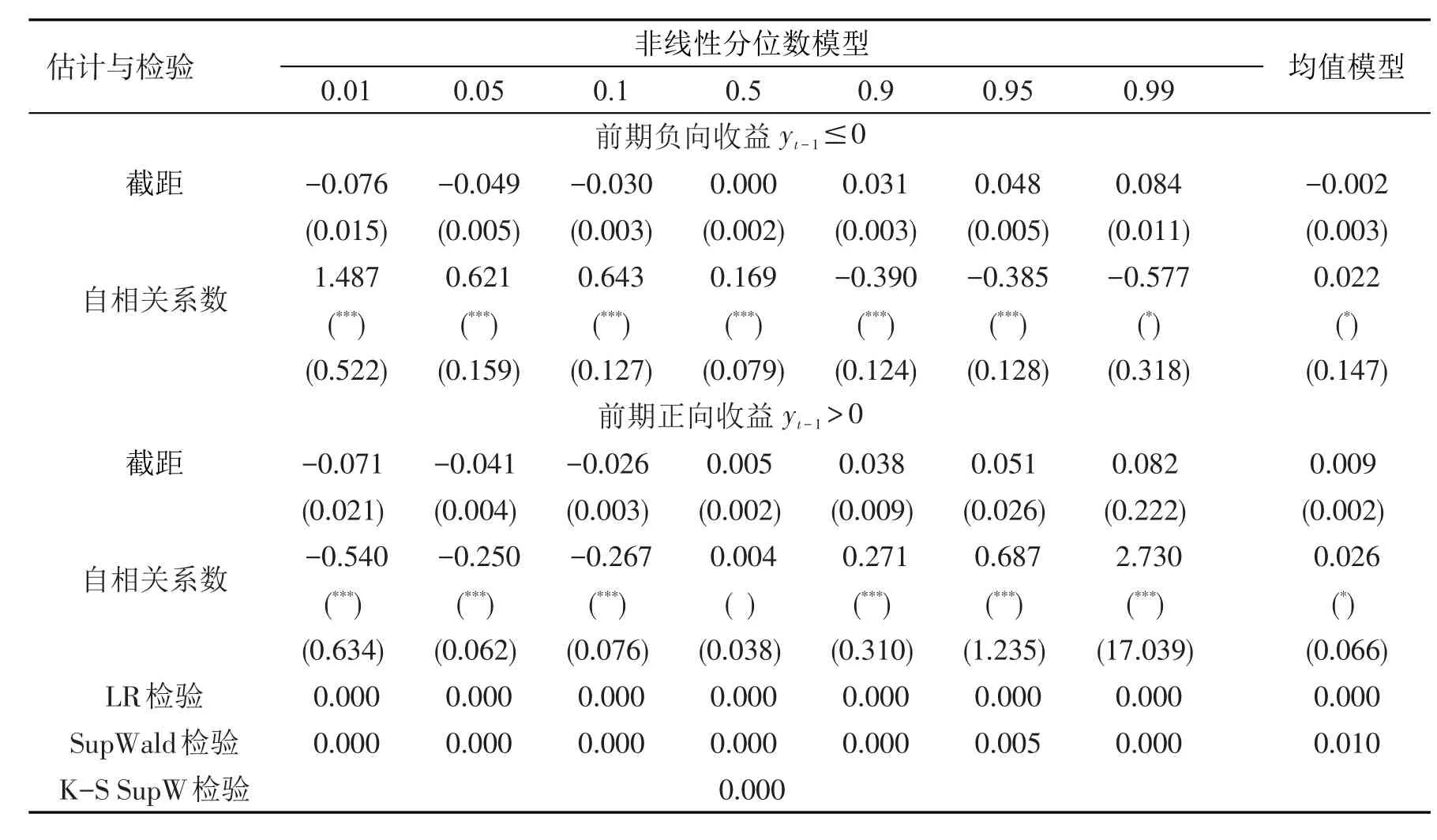
表3 周收益率的参数估计及诊断检验

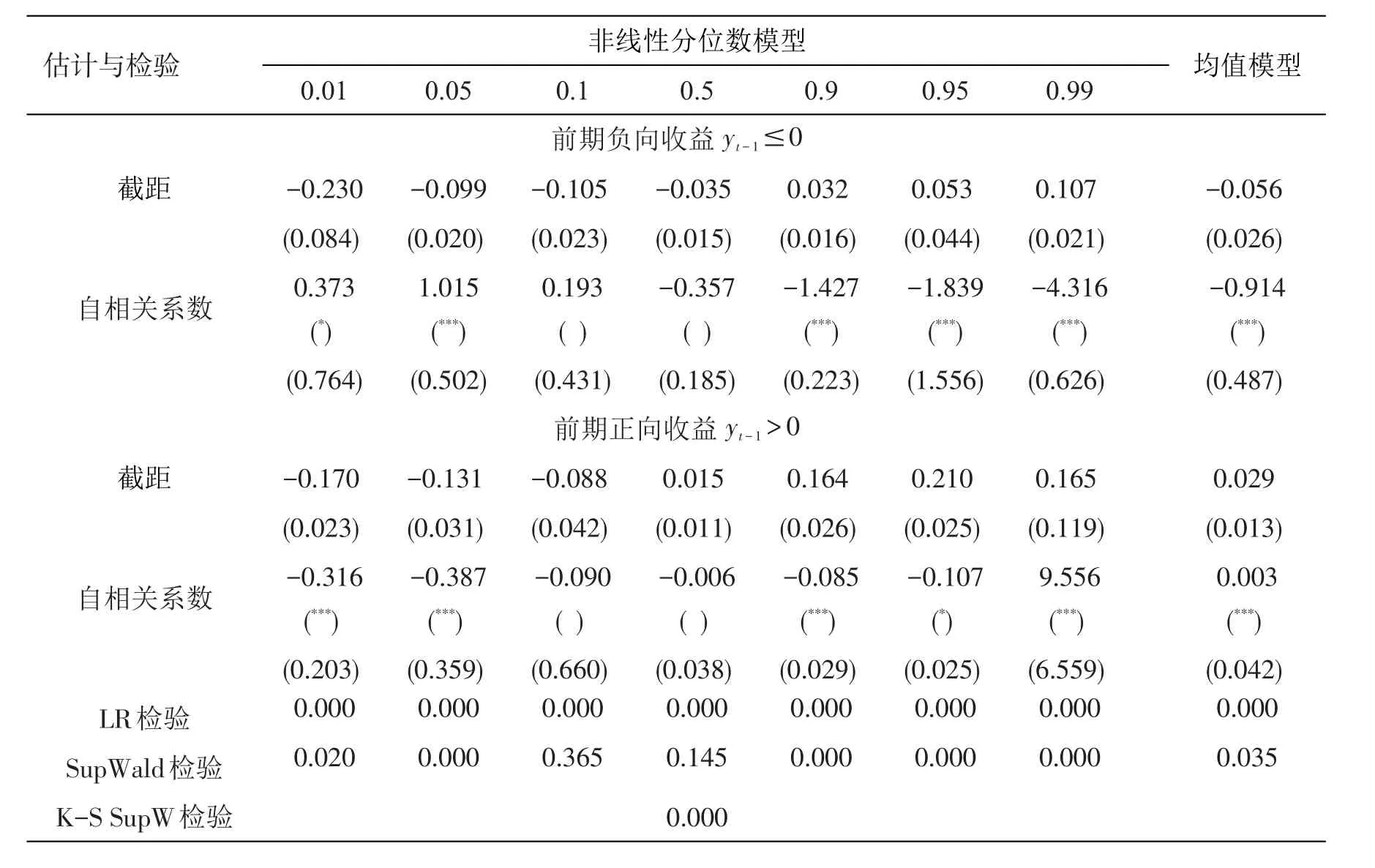
表4 月收益率的参数估计及诊断检验

3 小结

本文基于非线性分位数自回归模型，以正负向收益作为分段机制，分析中国股市收益的自相关特征。与传统的均值模型相比，本文中的模型不仅能度量当期收益对负向和正向前期收益的不同反应程度，而且能够捕捉收益序列的尾部分布特征，从而全面地刻画收益序列的非线性动态特征。实证结果表明，不同时间频率的收益序列在正负向收益的作用下，存在稳健的自相关特征，并且受市场环境（分位点）影响，呈现出典型的异质特征。具体表现为：

第一，自相关特征在正负向收益的冲击下表现不同。当前期收益为负向时，从低分位点到高分位点，收益序列由正自相关逐渐变为负自相关；而当前期收益为正向时，结论与之相反。

第二，收益序列自相关强度受分位点影响。在尾部分位点处（极端市场环境下）自相关性较强，在中位点处（温和市场环境下）自相关性较弱。

以上结论从侧面反映了中国股市还不够成熟的现状，仅在温和市场环境下收益序列的自相关性较弱，相对符合弱势有效性；而在极端市场环境下，收益序列自相关性较强，表明市场对新信息的反应不够迅速，容易出现金融异像。其原因在于，一方面，尽管我国股票市场近年来发展迅速，但仍处于发展的初级阶段，与成熟的资本市场相比差距较大；另一方面，市场中存在大量中小投资者，其非理性的“跟风”炒股行为，进一步加剧股票价格的非正常波动；此外，市场信息披露制度和相关政策不够完善，市场信息未能迅速准确流动，从而导致股票价格难以充分反映市场上的收益率、交易量等公开信息。

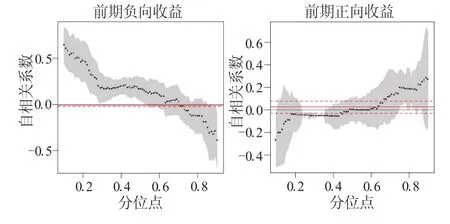
图2 周收益率的自相关系数估计图

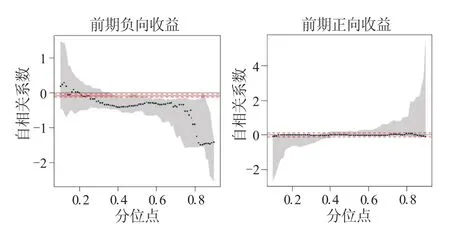
图3 月收益率的自相关系数估计图

因此基于上述分析，建议从以下几方面进行改进。第一，建立有效的市场机制。我国股票市场需进一步丰富交易品种和产品结构，改善交易方式及交易手段，提高交易速度，降低交易成本，建立合理的市场准入及退出机制，从而不断提高市场竞争力，使价格对极端市场的反映更加灵敏、迅捷，促进市场由低效到高效的转化。第二，增强理性投资观念。目前股票市场上普遍缺乏理性投资者，“跟风”现象仍较为严重，投资者的风险意识及投资理念仍不够成熟，因此有必要进一步提高投资者对市场信息的分析能力，减少非理性行为发生，尽量避免盲目投机行为导致的股价非理性波动。第三，强化信息披露制度。完备的市场披露制度是市场效率的重要保障。目前，我国股票市场在披露范围、披露主体、披露渠道和披露管理等方面还存在若干问题，有必要进一步完善市场披露制度，尽量避免信息资源的非对称性，保证市场信息的公平获取，严厉惩治内幕信息内幕交易等行为，为投资者创造良好成熟投资交易环境。第四，完善政策法规建设。进一步加强政府对股市监管的宏观调控，加强市场监管的政策法规完善，灵活应对国内外金融重大事件对市场的可能冲击，尽量避免出现股价过度波动和资源无效分配，从而为市场的持续健康发展提供有力保障。

参考文献：

[1]Fama E F.Efficient capital markets:A review of theory and empirical work[J].The Journal of Finance,1970,25(2):383-417.

[2]Tversky A,Kahneman D.The framing of decisions and the psychology of choice[J].Science,1981,211(4481):453-458.

[3]Bondt W F,Thaler R.Does the stock market overreact?[J].The Journal of Finance,1985,40(3):793-805.

[4]Campbell J Y,Grossman S J,Wang J.Trading volume and serial correlation in stock returns[J].The Quarterly Journal of Economics,1993,108(4):905-939.

[5]Lewellen J.Momentum and autocorrelation in stock returns[J].Review of Financial Studies,2002,15(2):533-564.

[6]田诗成,郭 丽.考虑方差结构突变的股市收益波动非对称性研究[J].系统科学与数学,2014,34(6):653-662.

[7]李云红,魏 宇,吴晓雄.中国股票市场适应性特征的实证研究[J].管理工程学报,2016,30(1):72-79.

[8]严太华,陈明玉.基于马尔科夫切换模型的上证指数周收益率时间序列分析[J].中国管理科学,2009,17(6):33-38.

[9]朱慧明，蒋 超，刘利枚.基于极端分位回归的股市收益与交易量相依性研究[J].财经理论与实践，2017,38(208):39-44

[10]许启发，伯仲璞，蔣翠侠.基于分位数Granger因果的网络情绪与股市收益关系研究[J].管理科学,2017,30(3):147-160.

[11]欧阳敏华,雷钦礼.一般门限非对称误差修正模型的估计与检验[J].统计研究,2013,30(10):97-107.

[12]Baur D G,Dimpfl T,Jung R C.Stock return autocorrelations revisited:A quantile regression approach[J].Journal of Empirical Finance,2012,19(2):254-265.

[13]Koenker R,Bassett Jr G.Regression quantiles[J].Econometrica:Journal of the Econometric Society,1978,41(1):33-50.

[14]Koenker R,Xiao Z.Quantile autoregression[J].Journal of the American Statistical Association,2006,101(475):980-990.

[15]Galvao A F,Montes-Rojas G,Jose O.Threshold quantile autoregressive models[R].Working Paper,2008.

[16]Koenker R,Machado J A.Goodness of fit and related inference processes for quantile regression[J].Journal of the American Statistical Association,1999,94(448):1296-1310.