冷气侧对流传热系数周期性波动对固体温度分布影响的一维分析

施能博， 张温宇， 孙志新， 林 立

(福州大学石油化工学院， 福建 福州 350116)

0 引言

燃气轮机的效率提升主要通过提高涡轮进口温度实现， 目前先进燃气轮机的涡轮进口温度已远超过涡轮材料的耐受温度， 因此必须对高温部件进行有效的冷却， 以保证各部件的最高温度与温度梯度在允许范围内.

传统关于内部冷却空气系统的研究多专注于设计工况或非设计工况的稳态分析， 随着研发水平的不断提高， 非定常效应逐渐成为研究的关注点. Zimmer等[1]考察了将非定常冲击射流引入燃气轮机透平叶片冷却的效果， 结果表明斯特劳哈数小于一定值的情况下， 非定常射流冲击效果弱于稳态射流. Scherhag等[2]通过实验和数值研究， 考察了脉冲射流冲击对透平冷却应用的可行性及其对各类参数的敏感程度，脉冲来源为动叶造成的周期性非定常压力分布， 研究主要围绕流场的时变特征展开， 实际燃机中级压比更大， 因而能造成更强的脉冲射流. Hwang等[3]采用数值模拟进行了稳态和非稳态情况下气热耦合分析， 研究重点关注了非定常气热耦合分析对热负荷分析的影响及叶片寿命评估的影响. Schmidt等[4]也同样考察了非定常流动下的气热耦合问题， 开发了一个理论模型用于表征非定常的对流换热， 并用一个透平静叶的CFD模拟验证了该模型， 研究还表明， 非定常壁温对于时均的热负荷影响较小. 另一方面， 非定常流动强化换热的基础研究也日渐成熟， 通过合理的设计非定常流动可以在不增加冷气用量的基础上强化换热， 这也将为燃气轮机设计水平的进一步提高提供新的思路.

总体而言， 目前关于燃机内冷却空气系统的非定常效应影响的研究并不多见， 气热耦合情况下冷却系统的非定常现象对于高温部件温度分布的影响尚不明确. 本研究针对非定常边界下的一维导热问题， 通过求解无量纲方程， 揭示固体温度在边界发生周期性扰动情况下的变化特征， 及其中的关键影响因素. 基于无量纲数的一维分析结果， 可以方便地应用于工业设计, 以快速分析材料及几何尺寸对问题的影响.

1 数学模型

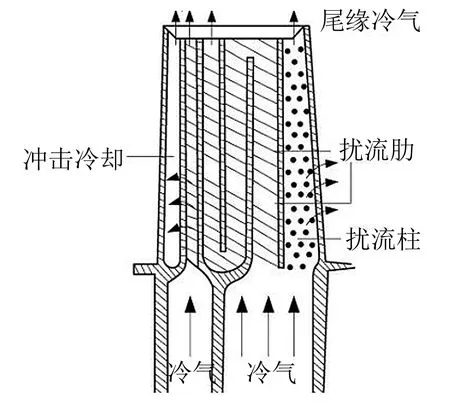
图1 燃气轮机透平叶片冷却结构[5] Fig.1 Turbine blade cooling structure ofthe gas turbine

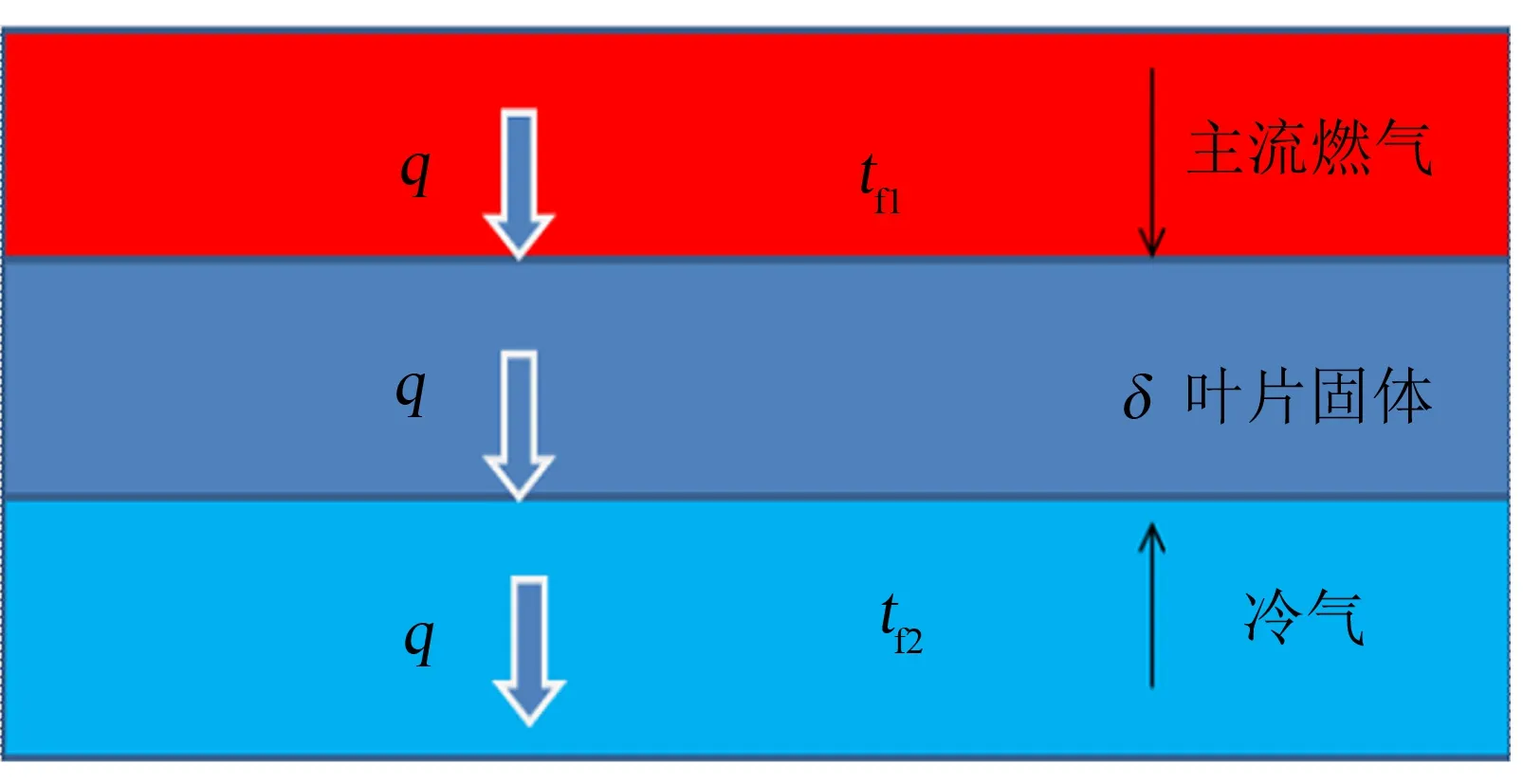
图2 一维传热示意图Fig.2 Schematic view of a one-dimensional heat transfer

燃气轮机高温部件的冷却， 主要有内部对流冷却和外部气膜冷却两种形式[5]， 典型的涡轮叶片冷却系统如图1所示. 考虑沿叶片壁厚方向的传热问题， 其包含3个传热过程： 主流燃气侧对流换热(研究不考虑辐射换热与气膜冷却)、 叶片内部固体导热和冷气侧对流换热. 为了简化问题并尝试从理论上找出控制各参变量变化的因素， 定性分析各控制因素对数学模型结果的影响， 又因为对于局部等温线与叶片几何边界近似平行的区域， 可认为局部传热是近似一维的， 所以研究仅考虑沿叶片壁厚方向的一维导热， 如图2所示， 并做如下假设.

1) 固体导热系数为常数. 该假设使得计算结果中, 固体内部温度时均值的空间分布由非线性变为线性， 而局部温度波动造成的导热系数波动幅值一般不超过2%， 因此该假设对于温度幅频特性的影响可以忽略.

2) 热流体侧边界条件为定常状态. 研究目的是研究冷流体侧的边界条件波动对传热过程的影响， 因此热流体侧边界条件设为定常.

由此建立数学模型， 考察冷气侧对流换热系数周期性变化对固体内温度分布的影响.

微分方程及边界条件如式(1)～(3)所示， 式中各变量含义参考文后符号列表[6].

(1)

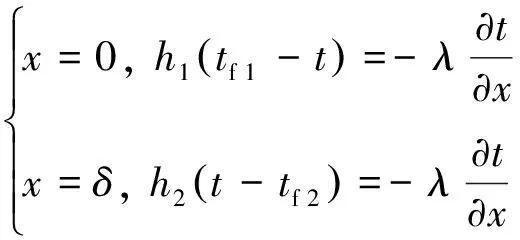
(2)

其中:

(3)

则该问题的解可表示为t=f(x,τ,a,λ,δ,h1,h2,tf1,tf2).

为了确定该问题的关键影响因素， 对上述方程进行无量纲化， 令

则微分方程及边界条件可整理为：

(4)

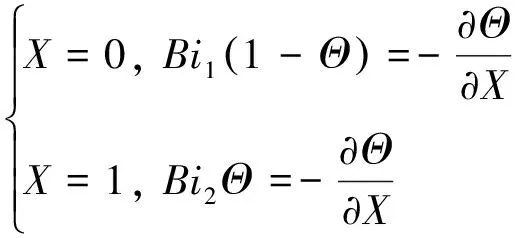
(5)

其中

(6)

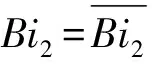
2 解的特征

由于一维非稳态导热方程式(4)关于Θ是线性的， 则在周期性的边界条件下， 该方程的解可表示为

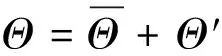
(7)

(8)

(9)

采用分离变量法可以对式(9)进行求解， 假设解的形式如式(10)所示:

Θ′=f(Fo)g(X)

(10)

代入式(9)求解， 整理后可求得

(11)

式中:A、B、C和n均为常量. 特别地， 若给定周期性变化的第一类边界条件， 则有

(12)

式中:ωFo, n为Θ关于Fo的波动角速度 (rad·s-1); 系数Tfw, n与Tbw, n根据边界条件确定， 分别影响向X正负方向传播的波动幅值.

(13)

本文所研究问题即为第三类边界条件中对流传热系数周期性波动而流体温度保持常量的情形， 因此虽然方程(4)的解具有式(12)的形式， 但其中系数A、B无法直接通过边界条件确定， 因此采用数值求解的方法进行分析.

此外， 对流传热系数随时间周期性变化带来的边界条件非线性， 也将对传热强化或削弱有所贡献. 为便于理解， 此处以量纲参量表示， 如式(14)所示， 时均的传热量并不等于时均的对流传热系数与时均温差的乘积， 而是多了一项协方差项， 协方差项的正负将使得非定常情况下传热量大于或小于定常情况. 注意到式(14)中，h和(Tw-Tf)的乘积是两个周期性信号的乘积， 将产生额外的频率分量， 亦即， 即使边界传热系数的波动仅有一个频率分量， 由此产生的固体温度波动及传热量波动也将包含多个频率分量.

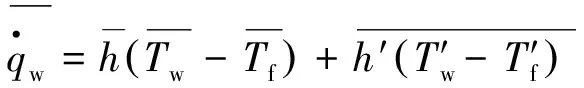
(14)

3 数值求解及结果分析

3.1 数值求解参数设置

由于以燃气轮机高温部件冷却为研究背景， 因此第2节中数学模型的相关系数， 应根据相应的实际情况选取， 以确保各无量纲参数处于合理范围. 表1给出了Mark II翼型实验的相关参数[7]， 其中壁厚及对流传热系数的数据取自叶片前缘滞止区， 并忽略固体导热系数随温度变化， 以此为基础进行计算. 特别地， 冷气侧对流传热系数的波动幅值取为时均传热系数值的20%， 波动周期为1 s. 表2给出了数值计算所需的无量纲系数.

数值求解采用Matlab软件提供的pdepe函数基于线上法(method of lines)对一维抛物型和椭圆型方程进行求解， 即采用近似方法对偏微分方程的空间微分项进行离散， 从而将偏微分方程转化为不再显含空间独立变量的常微分方程组， 具体计算方法参考文献 [8-10]. pdepe函数计算过程中, 对时间项的积分采用自动时间步长和格式， 对空间项离散采用基于网格尺寸的二阶精度格式. 计算中时间长度的选取保证固体内部温度分布已进入稳定的周期性变化阶段， 空间网格数的选择经过了网格无关性测试. 计算结果表明空间网格数取128和256时计算结果几乎相同， 因此后续计算分析基于空间网格数128进行.

表1 Mark II翼型实验参数

表2 数值计算所需无量纲系数

3.2 固体温度变化过程及时均值

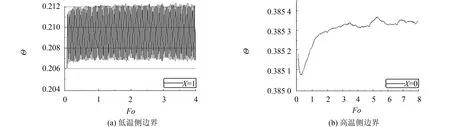
图3 边界温度变化过程(以时的稳态解为初值)Fig.3 Changing processes of boundary temperature(stationary solution to the as the initial value)

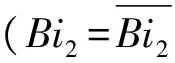
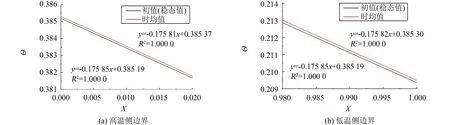
图4 固体温度时均值分布Fig.4 Distribution of the time-average of solid temperature

图5给出了固体两侧边界温度稳定周期性波动阶段的傅里叶分析结果. 由图5可知， 冷气侧温度波动幅值的峰值对应的频率与该侧毕渥数Bi2关于傅里叶数Fo的波动频率fBi2相符， 而在此频率之外， 仍有一些幅值微小的频率分量， 其根本原因在于式(4)～(6)构成的数学模型关于Θ的非线性， 这与图3中的温度变化趋势一致， 也与第2节中的分析相符. 而固体高温侧边界温度变化的傅里叶分析结果中， 对应fBi2频率处仍有明显的峰值， 但其幅值已与其余频率分量的幅值大致相当， 因此图5中高温侧温度随时间的变化并不像低温侧一样在fBi2频率下呈现明显的正弦波动.

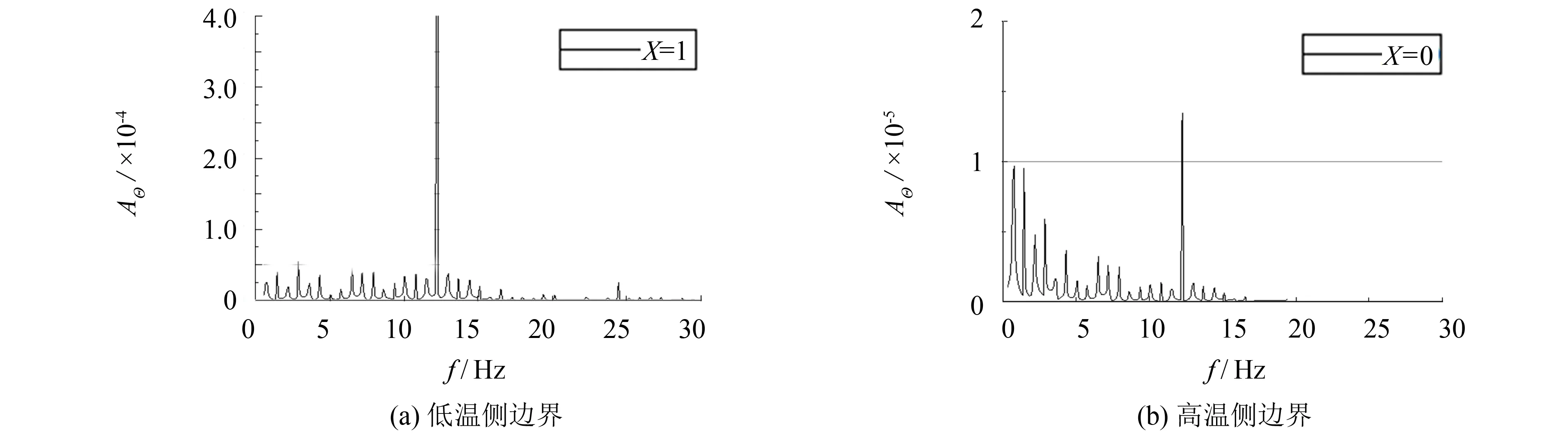
图5 固体边界温度波动频谱分析Fig.5 Spectral analysis of the solid boundary temperature fluctuations

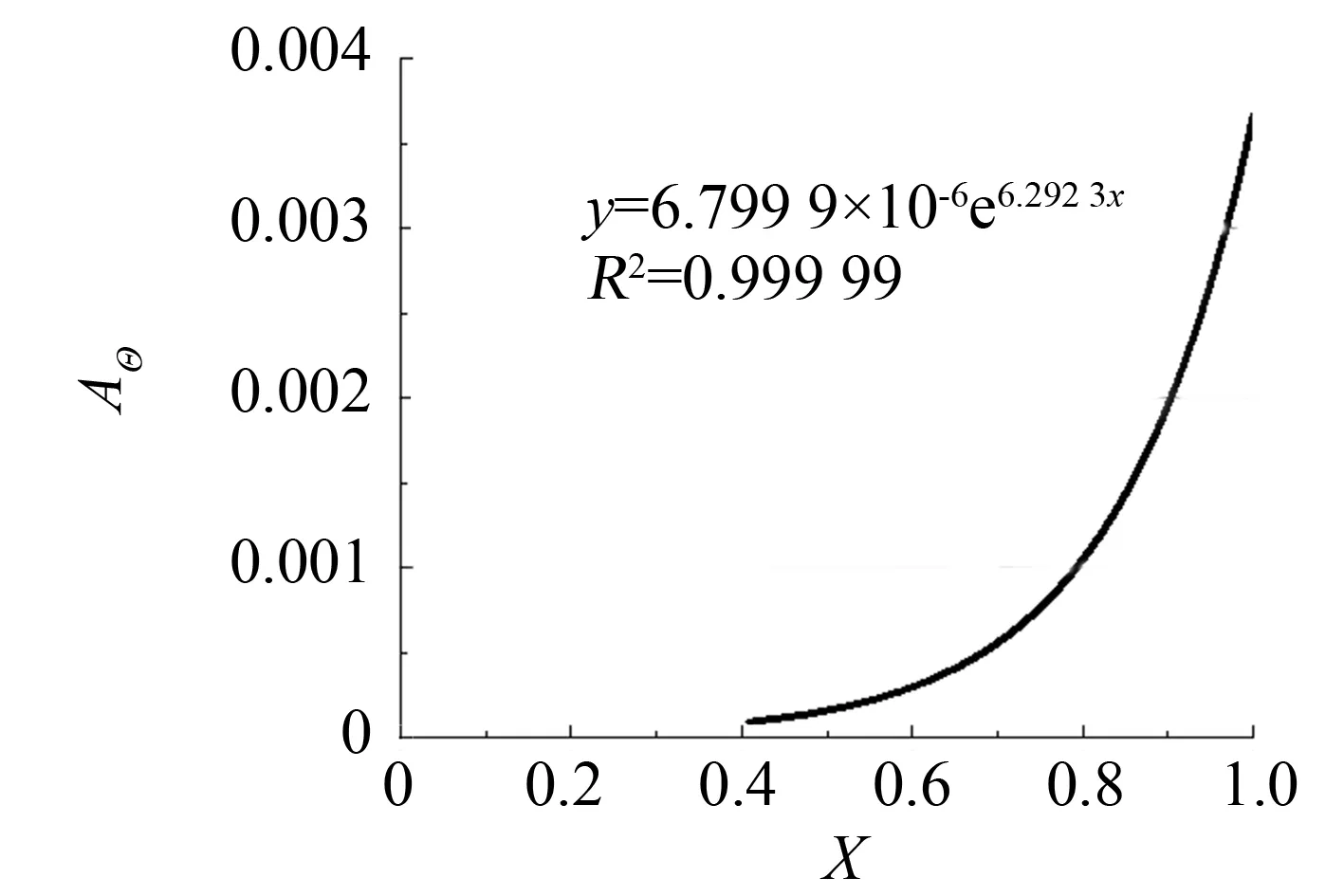
图6 固体内部各处温度波动幅值的分布 Fig.6 Distribution of temperature fluctuation amplitude in solid

由于固体温度波动均在fBi2频率下存在最大幅值， 因此对于温度波动幅值的分析仅考虑该频率. 图6显示了固体温度稳定周期性变化阶段各处温度波动在fBi2下的幅值分布. 由图6可知， 固体冷气侧边界由于受冷气对流传热系数周期性变化的直接影响， 其温度波动幅值最大， 而与冷气侧距离越远， 温度波动幅值越小. 由微分方程(4)的通解形式(12)可知， 温度波动幅值在固体内部以指数规律衰减(由于高温侧近似稳态， 因此仅考虑扰动向X负方向传播)， 将fBi2代入式(12)， 计算得温度波动幅值衰减的指数为6.2， 与图6拟合结果较为接近， 考虑到固体内温度波动是多个频率信号的叠加(如图5)， 仅由边界扰动频率fBi2来估计幅值衰减速率带来的偏差是可以接受的.

进一步地， 可以根据温度波动幅值的衰减定义穿透深度Xp， 参考文献[11]定义， 将穿透深度定义为温度波动幅值衰减为边界温度波动幅值10%的位置深度. 依此定义， 算例结果如图7所示， 穿透深度位置在X=0.625. 同样的， 根据式(12)， 可以推导得穿透深度的表达式如式(15)所示(由于高温侧近似稳态， 因此仅考虑扰动向X负方向传播)， 将fBi2代入(忽略其余频率分量)， 可估算得穿透深度位置为Xp=0.628 5， 与数值计算结果基本一致.

(15)

穿透深度的意义在于揭示边界周期性变化的影响范围， 前述算例的固体壁厚要大于冷气侧边界对流传热系数波动的穿透深度， 因此， 可近似认为高温侧壁温处于定常状态. 对于叶片中局部壁厚较薄的地方， 冷气侧对流传热系数波动对应的穿透深度可能大于固体壁厚， 此时高温侧壁温也将呈现明显的周期性变化.

3.3 边界条件非线性产生的换热削弱

上文第2节中分析了对流传热系数的周期性波动造成的边界条件非线性将对传热产生强化或削弱的效果， 如式(14)所示. 图8给出了数值计算结果中固体低温侧边界无量纲温度(Θ)、 无量纲传热量(QΘ=Bi2Θ)和毕渥数(Bi2)的变化过程， 由图可知三者波动的主频率是一致的(即fBi2)， 而三者波动存在明显的相位差. 当边界对流传热系数增大时， 将增大边界的传热量， 从而导致固体温度降低， 对流换热温差的减小又对换热量造成影响， 反之亦然. 总体而言， 对流传热系数增大的阶段大致对应传热量增大的阶段和固体温度降低的阶段， 由图8可知，Bi2的峰值时刻、QΘ的峰值时刻和Θ的谷值时刻三者并不严格重合， 但较为接近.

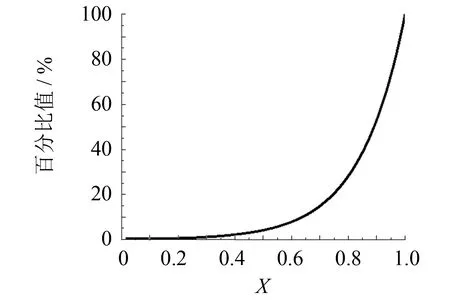
图7 某一时刻各位置下温度波动幅值与边界波动幅值的比值Fig.7 Each location at a certain moment under temperature fluctuation amplitude and the ratio of boundary wave amplitude

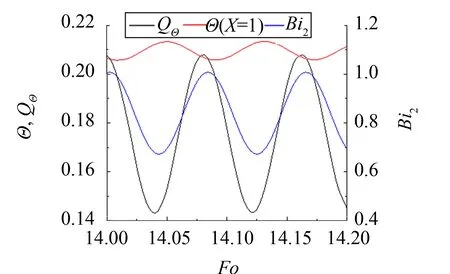
图8 固体低温侧边界上无量纲温度、 无量纲传热量和毕渥数随时间变化规律Fig.8 Dimensionless temperature, dimensionless heat transfer and Biot number change with time on the boundary of low temperature side

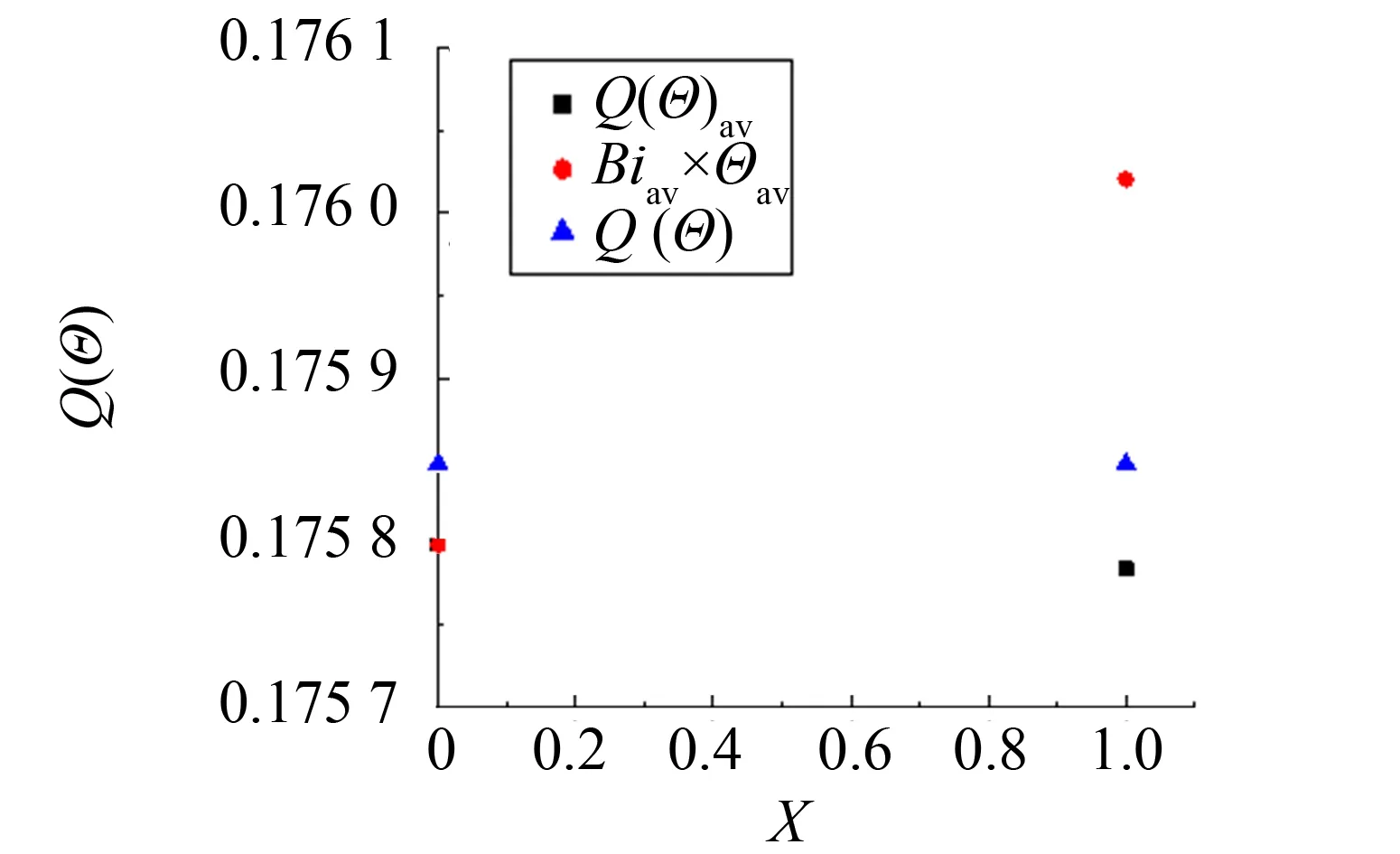
图9 固体边界上传热量的时均值Fig.9 Time-average of heat transfer on the boundary of low temperature side

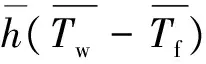
同时， 由图9可知， 稳态情况下， 经过固体的热量要略高于非定常情况， 这与图4中稳态情况下固体温度要略低于非定常情况是一致的. 这也意味着， 与稳态情况相比， 冷气侧对流传热系数的周期性波动削弱了整个系统的换热， 而这种削弱效应是由于固体温度场在周期性边界下的响应特征造成的， 而与流场细节无关.

3.4 无量纲参数分析

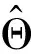
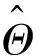
图10 两侧边界随ωFo的变化情况 changes with ωFo on both sides of the boundary

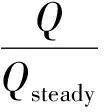
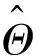
图11 低温侧换热削弱程度随ωFo的变化情况Fig.11 Extent of weaken heat transfer change with ωFo on the low temperature side

图12 高温侧边界随毕渥数Bi1的变化 changes with Bi1 on the high temperature side

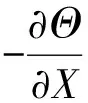
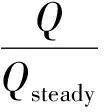
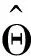
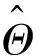
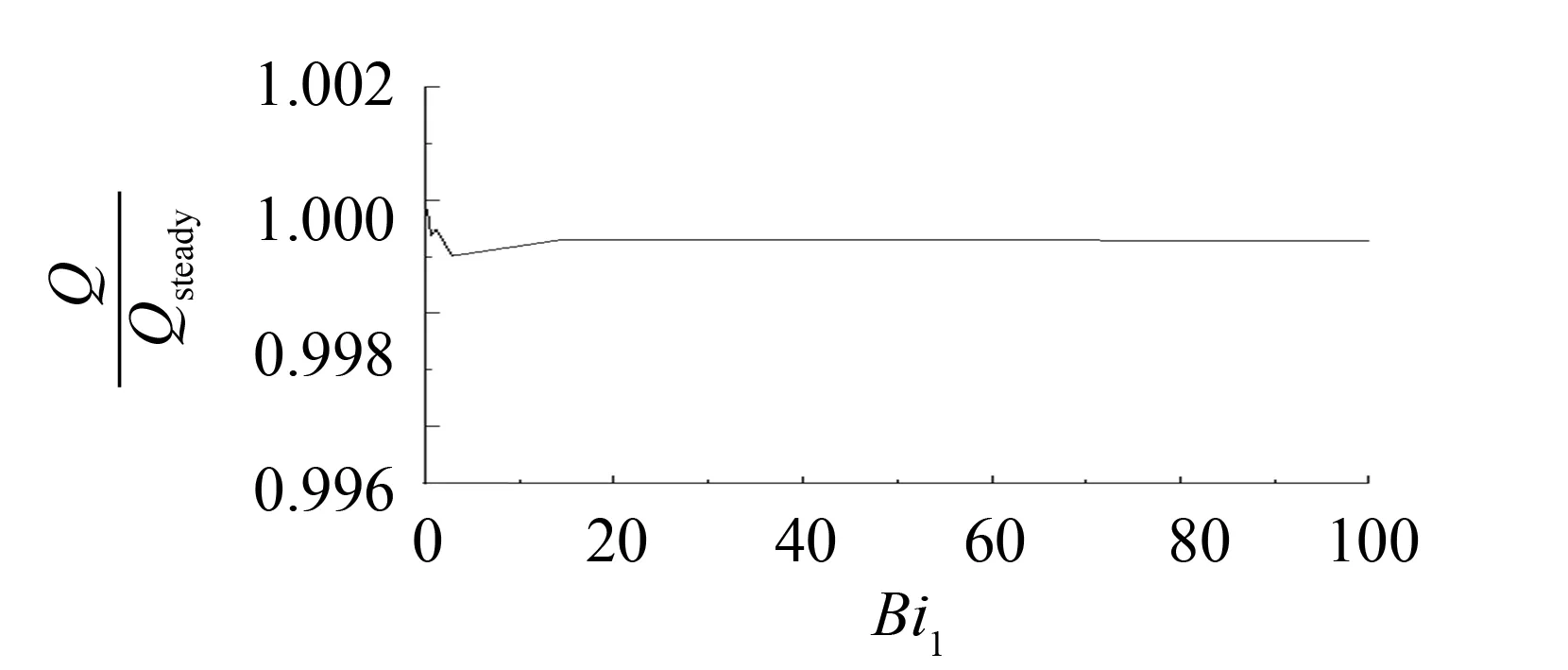
图13 高温侧换热削弱程度随Bi1的变化情况Fig.13 Extent of weaken heat transfer change with Bi1on the high temperature side

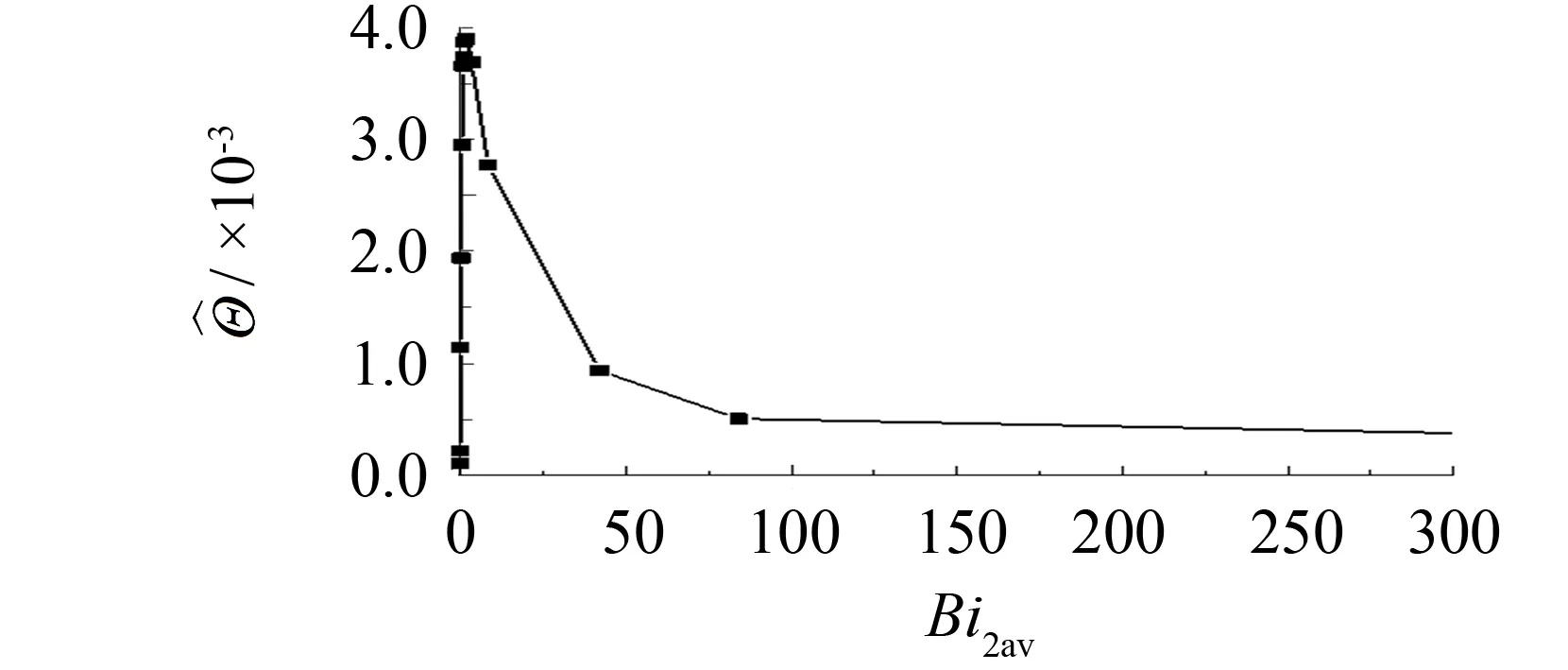
图14 低温侧边界随低温侧毕渥数时均值Bi2av的变化 with Bi2av on the low temperature side

图15 低温侧换热削弱程度随Bi2av的变化情况Fig.15 Extent of weaken heat transfer change with Bi2avon the low temperature side

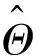
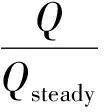
4 结语

对第三类边界发生周期性波动情况下的固体一维非定常导热问题进行研究. 首先对数学模型进行无量纲分析， 推导了第一类边界下的解析解形式， 而后根据燃机叶片工作条件进行数值实验. 结果表明：

根据这一发现，科学家研制出了“鲎试剂”，这种试剂能准确、快速地检测出革兰氏阴性菌的内毒素，可以广泛应用于医药卫生、食品安全和水质检测等和人类生活息息相关的领域。

1) 影响固体内部无量纲温度分布的主要因素包括： 无量纲位置X， 无量纲时间Fo， 以及固体两侧的毕渥数Bi1和Bi2；

2) 第三类边界条件的非线性会引起对流传热系数波动时壁面传热削弱， 其根源在于边界对流传热系数和温度变化之间的相位差；

3) 边界对流传热系数周期性变化对应的穿透深度主要受边界毕渥数变化频率fBi2或波动角速度ωFo的影响；

4) 关于Fo的波动角速度参量ωFo越小， 穿透深度越大， 传热削弱越明显； 扰动侧毕渥数Bi2存在某一取值， 使得扰动侧无量纲壁温波动幅值最大.

参考文献：

[1] ZIMMER V J, RUTLEDGE J L, KNIERIEM C,etal. The influence of coolant unsteadiness on impingement heat transfer[C]//ASME Turbo Expo. Duesseldorf: ASME, 2014.

[2] SCHERHAG C, GEIERMANN J P, WARTZEK F,etal. Blade triggered excitation of periodically unsteady impinging jets for efficient turbine liner segment cooling[J]. Journal of Turbomachinery, 2015, 138(5): S15.

[3] HWANG S, SON C, SEO D,etal. Comparative study on steady and unsteady conjugate heat transfer analysis of a high pressure turbine blade[J]. Applied Thermal Engineering, 2016, 99: 765-775.

[4] SCHMIDT M, STARKE C. Coupled heat-transfer simulations of turbines in consideration of unsteady flows[J]. International Journal of Thermal Sciences, 2015, 96: 305-318.

[5] 韩介勤， 杜达， 艾卡德. 燃气轮机换热和冷却技术[M]. 程代京， 谢永慧, 译. 西安: 西安交通大学出版社， 2005.

[6] 杨世铭， 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社， 2006: 41-44.

[7] HYLTON L D, MIHELC M S, TURNER E R,etal. Analytical and experimental evaluation of the heat transfer distribution over the surfaces of turbine vanes[C]//Aas/Division of Dynamical Astronomy Meeting. Indianapolis: Final Report Detroit Diesel Allison, 1983.

[8] SKEEL R D, BERZINS M. A method for the spatial discretization of parabolic equations in one space variable[J]. SIAM Journal on Scientific and Statistical Computing, 1990, 11(1): 1-32.

[9] HOWARD P. Partial differential equations in MATLAB 7.0[M]. Maryland: University of Maryland, 2005.

[10] 董平， 黄洪雁， 冯国泰. 高压燃气涡轮径向内冷叶片气热耦合的数值分析[J]. 航空动力学报, 2008, 23(2): 201-207.

[11] BERGMAN T L, LAVINE A S, INCROPERA F P,etal. Fundamentals of heat and mass transfer[M]. New Jersey: John Wiley & Sons, 2011.

[12] JAWORSKI A J, PICCOLO A. Heat transfer processes in parallel-plate heat exchangers of thermoacoustic devices-numerical and experimental approaches[J]. Applied Thermal Engineering, 2012, 42(2): 145-153.

[13] INCROPERA F P, DEWITT D P, BERGMAN T L,etal. Fundamentals of heat and mass transfer [Hardcover][J]. Staff General Research Papers, 2006, 27(1/2): 222.

[14] SCHLICHTING. Boundary layer theory[M]. New York: Springer, 2000: 569-578.

[15] ZUDIN Y B. Analysis of the processes of heat transfer with periodic intensity with allowance for temperature fluctuations in the heat carrier[J]. J Eng Phys Thermophys, 2000, 73(2): 243-247.