图像线状和网格状噪声的去除方法

陶 胜

在图像获取、传输、接收和处理的过程中，会不可避免地受到各种噪声的干扰和影响，这不仅影响图像的视觉效果，降低图像质量，而且由于噪声使图像信息丢失，严重影响了后续的图像处理过程。去除噪声的主要方法是图像滤波，根据处理的空间不同，分为空域法和频域法。空域法是直接在图像所在的像素空间进行信息处理，而频域法是对图像进行正交变换后在频域上进行信息处理。

传感器等电子元件在图像获取过程中会产生线状和网格状噪声［1］。下面探讨在频域和空域去除线状噪声和网格状噪声的方法：对图像进行频率分析，采用陷波滤波器去除噪声，在此基础上检测出噪声像素点，尝试在空域上采用开关中值滤波方法以及退化模型去除噪声。

1 线状和网格状噪声及其频域分析

视频图像中的等间距线状和网格状噪声可以用如下模型描述：

其中MOD（）函数为求余函数，Ax和Ay分别为水平方向和垂直方向上的幅值常数，Δx和Δy分别是水平方向和垂直方向上的间隔常数。

当Ay为零时，噪声在图像上呈水平线状；当Ax为零时，噪声呈垂直线状；当Ax和Ay均不为零时，噪声形状呈现出网格状。图1和图2分别给出了水平线状噪声和网格状噪声图像。

图1 叠加水平线状噪声的Lenna图

图2 叠加网格状噪声的Lenna图

对叠加水平线状噪声的图像进行二维离散傅里叶变换后得到的傅立叶频谱如图3所示。在图3中，噪声对应的是纵轴上的一些亮点。与之类似，对叠加垂直线状噪声的图像进行二维离散傅里叶变换后，噪声对应的是频谱图中横轴上的一些亮点。对叠加网格状噪声的图像进行二维离散傅里叶变换后得到的傅立叶频谱如图4所示。图4中噪声对应的是坐标轴上的一些亮点，并且这些亮点关于原点对称。而直接对Lenna图像进行二维离散傅里叶变换后得到的傅立叶频谱图不会出现这些亮点，这说明线状和网格状噪声分布具有准周期性。

图3 叠加水平线状噪声的Lenna图频谱

图4 叠加网格状噪声的Lenna图频谱

2 频域陷波滤波

频域滤波的过程是先对图像进行正交变换（常用的是傅里叶变换），再对正交变换得到的正交变换域系数阵列进行滤波处理，然后逆变换到空域，得到处理结果图像［2］。

傅里叶变换是把图像从空域变换到频域，图像的背景区域和缓慢变化部分对应频谱中的低频部分，而边缘、细节、跳跃部分以及噪声则对应高频部分［2］。线状和网格状噪声具有准周期性，噪声频谱与图像的频谱是可分离的，因此对于带有此类噪声的图像，可以通过频域滤波的方法来去除噪声。常用的频域滤波器有高通滤波器、低通滤波器、带阻滤波器和陷波滤波器等［3］。这些滤波器的默认低频位置都是在图像的中心。

2.1 陷波滤波器

陷波滤波器只针对某些特定的频率点周围的频率进行抑制。相比于其他滤波器，陷波滤波器能更有效地消减线状和网格状噪声。在计算傅立叶变换时，坐标原点选在图像的中心位置处。由于傅里叶变换是关于坐标原点对称的，而且需要抑制的频率点也关于原点对称，要获得有效结果，陷波滤波器就必须以关于原点对称的形式出现。

常用的三种陷波滤波器的传递函数［3］有：理想陷波滤波器

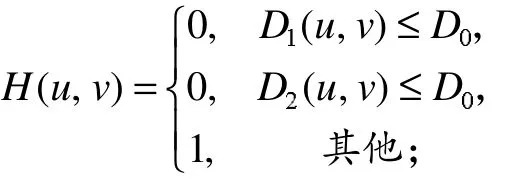
巴特沃斯陷波滤波器

高斯陷波滤波器

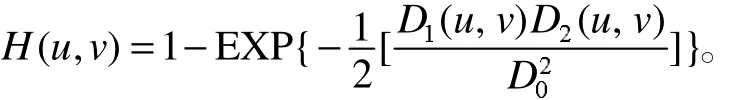
设 p1（u0，v0）和 p2（-u0，-v0）是一对需要抑制的频率点，则可以选择陷波区域的形状是以p1和p2为中心的圆，D0是圆的半径，n为阶数。假设图像大小为M×N像素，频率矩形的中心点为，则

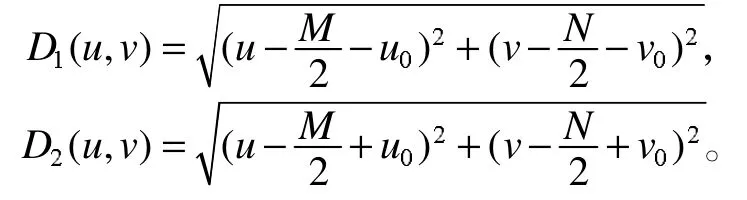
需要说明的是，上述陷波滤波器只给出了一对需要抑制的频率点（u0，v0）和（-u0，-v0），而可实现的陷波滤波器的对数可以是多对，且陷波区域的形状也可以是其他形状，如矩形理想陷波滤波器的传递函数为：

这里的w和h分别为矩形的半宽和半高。

2.2 亮点的检测和陷波滤波器参数的确定

采用陷波滤波器去除线状和网格状噪声的关键在于如何准确地定位噪声对应的亮点并确定陷波滤波器参数。

对图1所示的叠加了水平线状噪声的图像进行傅里叶变换后，得到如图3所示的傅立叶频谱。以其纵轴上各点的位置为横坐标（自上而下），以各点的频谱值为纵坐标，绘制的频谱曲线如图5所示。

图5中的中心点及其附近点均是亮点，但不是噪声所对应的，这是因为中心点表示图像的平均亮度。因此，将检测范围限制在不包含中心点附近部分的区域。寻找各点（不包含中心点及其附近）频谱值的最小值和最大值，分别记为 Tmin和 Tmax，令 T=Tmin+3（Tmax-Tmin）/4，如果某点的频谱值是局部最大值（即大于与它相邻点的频谱值）且其值大于等于T，那么该点的位置就是亮点中心。计算每个亮点中心与其左侧第一个谷底（局部最小值所对应的点）之间的距离，记为D1；与其右侧第一个谷底（局部最小值所对应的点）之间的距离，记为D2。D1和D2中的最大值作为陷波滤波器的带宽半径，这就是所需要的陷波滤波器参数（实际应用时可适当增大一些，陷波效果更好）。

同理，对叠加了垂直线状噪声的图像进行傅里叶变换后，检测其频谱图横轴上的亮点并确定陷波滤波器参数。对图2所示的叠加网格状噪声的图像进行傅里叶变换后，得到如图4所示的傅立叶频谱，分别检测其频谱横轴上和纵轴上的亮点，并确定陷波滤波器参数。

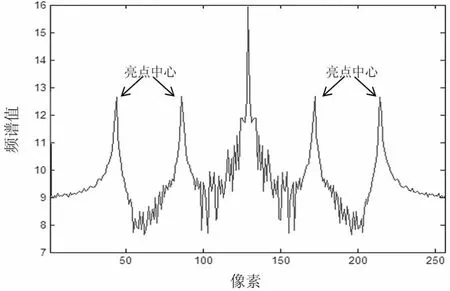
图5 频谱曲线图

2.3 陷波滤波

检测出噪声对应的亮点位置和确定陷波滤波器参数后，分别采用理想陷波滤波器、巴特沃斯陷波滤波器、高斯陷波滤波器进行滤波。其中高斯陷波滤波器去除水平线状噪声的结果如图6所示，去除网格状噪声的结果如图7所示。

图6 高斯陷波滤波器去除水平线状噪声图

3 空域复原

从图6和图7可以看出，采用陷波滤波的效果并不理想，周围区域的噪声没有被完全去除。为了取得更好的去噪效果，下面探讨如何在空域去除线状和网格状噪声。

3.1 检测噪声像素

假定含噪声的灰度图像为 f（x，y），行数为 M，列数为N。令F为噪声标志矩阵，其行数为M，列数为N，元素全部初始化为1。计算有水平线状噪声图像每行所有像素点亮度的和，如果该和值与其上、下相邻两行的和值的差均大于等于给定的阈值，则该行的各像素点均为噪声像素，其标志矩阵对应的值将被修改为0。计算有垂直线状噪声的图像每列各像素点亮度的和，如果该和值与其左、右相邻两列的和值的差均大于或等于给定的阈值，则该列的各像素点均为噪声像素，其标志矩阵对应的值将被修改为0。类似地，对于网格状噪声图像，就对其各行、各列分别进行检测，得到噪声标志矩阵。

3.2 开关中值滤波

开关中值滤波器［4］是先检测噪声像素，然后只对检测到的噪声像素进行中值滤波，而被判断为非噪声的像素则不再参与中值滤波。为了能处理图像边缘部分的点，先要扩展噪声图像和噪声标志矩阵（重复噪声图像矩阵和噪声标志矩阵第一行、最后一行、第一列和最后一列），扩展后的噪声图像和噪声标志矩阵大小均为（M+2）×（N+2），然后考察扩展后的噪声图像的每一像素点及其周围8个像素点，去掉这9个点中对应标志为0的点（噪声点），将剩余点（非噪声点）的像素值的中值作为输出,最后将边缘部分（第一行、最后一行、第一列、最后一列）去掉后的剩余部分作为开关中值滤波结果。开关中值滤波去除网格状噪声的图像的结果如图8所示。

图8 开关中值滤波去除网格状噪声图

3.3 基于退化模型去除噪声

令原始图像为 f0（x，y），线状和网格状噪声为n（x，y）=Ax（MOD（x，Δx）==0）+Ay（MOD（y，Δy）==0），则退化图像为 f (x,y)=f0(x,y)+n(x,y)。基于退化模型去除噪声方法就是利用开关中值滤波估计模型中的未知参数，根据模型得到去噪图像。

图9 退化模型去除网格状噪声图

4 仿真实验分析

通常使用峰值信噪比（PSNR）评价去噪效果［5］。PSNR越高,相应去噪方法的性能就越好。

采用MATLAB R2012a作为开发工具，在Windows XP平台下实现线状和网格状噪声的频域陷波滤波去噪、空域开关中值滤波去噪和基于退化模型去噪。仿真实验以Lenna作为原图，分别添加幅值为35、间隔为6的水平线状噪声，幅值为30、间隔为5的垂直线状噪声，水平方向幅值为25、间隔为5和垂直方向幅值为25、间隔为5的网格状噪声。分别计算出理想陷波滤波、巴特沃斯陷波滤波、高斯陷波滤波和开关中值滤波以及基于退化模型复原的PSNR，结果如表2所示。

表2 频域和空域去除线状和网格状噪声的PSNR dB

由表2可知：采用开关中值滤波的PSNR比采用陷波滤波的PSNR高出约2～9 dB。可见，对于水平线状噪声、垂直线状噪声和网格状噪声，采用开关中值滤波能够取得比陷波滤波更好的去噪效果。采用退化模型复原的PSNR比采用开关中值滤波的PSNR高出约29～42 dB。可见，采用退化模型复原能够取得更好的去噪效果。

5 结束语

陷波滤波是去除线状噪声和网格状噪声的有效方法，亮点的检测和陷波滤波器参数的确定对图像去噪起着非常重要的作用。仿真实验表明：采用理想陷波滤波器、巴特沃斯陷波滤波器和高斯陷波滤波器去除线状噪声和网格状噪声的差别不大。采用开关中值滤波和退化模型复原能够取得比陷波滤波更好的去噪效果，与陷波滤波去噪方法相比，在客观评价标准和主观视觉效果方面均较好。

参考文献：

［1］ 武楠，王珩.一种视频监控图像条纹噪声去除算法［J］.电子设计工程，2012，20（9）：190-192.

［2］ 李云红，屈海涛.数字图像处理［M］.北京：北京大学出版社，2012：107-119.

［3］ 杨杰，黄朝兵.数字图像处理及 MATLAB实现［M］.北京：电子工业出版社，2013：115-119.

［4］ 金良海，李德华.基于噪声检测的图像去噪算法［J］.模式识别与人工智能，2008，21（3）：298-302.

［5］ 姚敏.数字图像处理［M］.北京：机械工业出版社， 2012：118-120.