Behavior of ring footing resting on reinforced sand subjected to eccentric-inclined loading
Vaibhav Sharma,Arvind Kumar
Dr.B.R.Ambedkar National Institute of Technology,Jalandhar,144011,India
1.Introduction
Ring footings are suitable for the structures which are circular in plan and all the external or internal forces are transferred through their wall into the foundation before they get transferred into the ground.Tall transmission towers,chimneys,silos and oil storages are suggested to be founded on ring foundations.As ring footings are more suitable for these types of structures,which are supposed to be taller than the existing structures around them,these structures are more susceptible to horizontal loads/forces like wind loads.The ring foundation has to bear not only the vertical loads but also the horizontal loads.The combination of horizontal and vertical loads acting on the structure will result in an inclined load.Moreover,the location of horizontal load(centroid)anywhere along the height of the structure may produce eccentricity of the resultant load’s point.Hence,ring footings can be subjected to both eccentric and/or inclined loadings.Many investigators have studied the behaviors of footings resting on unreinforced and/or reinforced soil beds,other than ring footings subjected to eccentric and inclined loadings(Meyerhof and Hanna,1978;Sastryand Meyerhof,1987;Saran and Agarwal,1989,1991;Taiebat and Carter,2002;Hjiaj et al.,2004;Patra et al.,2006;El Sawwaf,2007,2009;Saran et al.,2007;Jao et al.,2008;Behera et al.,2013;Ornek,2014;Badakhshan and Noorzad,2015,2017a,b).From their studies,one can see that as the eccentricity of the load increased,the bearing capacity of the footing decreased significantly,and more tilting of footing was also observed.Reinforcing the soil,however,can improve the bearing capacity of footing,and reduce the settlement of footing.
The majority of experimental,numerical and/or analytical studies conducted on ring footings resting on reinforced and/or unreinforced soil beds merely focused on concentric loading(Bowles,1987;Al-Sanad et al.,1993;Ismael,1996;Boushehrian and Hataf,2003;Laman and Yildiz,2003,2007;Kumar and Ghosh,2005;Zhao and Wang,2008;Lee and Eun,2009;Benmebarek et al.,2012;Naderiand Hataf,2014;Kumarand Chakraborty,2015;Naseri and Hosseininia,2015;Lee et al.,2016;Keshavarz and Kumar,2017;Sharma and Kumar,2017a).Bowles(1987)used finite element(FE)method to calculate the bearing capacity and settlement of ring footing.Laman and Yildiz(2003)conducted model tests on ring footing resting on geogrid-reinforced sand.It was concluded that the ring footing with ratio of inner to outer radius of ring(ri/ro=0.3),which gave similar results as that of full circular footing,can be a good option from the economic point of view in practical applications.Zhao and Wang(2008)calculated the bearing capacity factorNγfor ring footings with different radius ratios using finite difference method.More recently,Keshavarz and Kumar(2017)used the stress characteristics method to obtain the bearing capacity factorsNc,NqandNγas functions of internal friction angle(φ)of soil andri/roof ring footing.From the literature review,it has been found that the optimumri/rovalue of ring footing which behaves similar or better performance than circular footing lies in the range of 0.2-0.4,which is not a unique value.
Very limited effort has been made to understand the behavior of ring footing subjected to eccentric loading(El Sawwaf and Nazir,2012).El Sawwaf and Nazir(2012)experimentally studied the behavior of eccentrically loaded ring footing resting on a compacted replaced geogrid-reinforced sand layer that overlies an extended loose sand layer.It was concluded that the reinforcement not only reduced the depth of replaced sand,but also increased the bearing capacity of eccentrically loaded ring footing significantly.
Hence,there is a need to study the effects of load eccentricity and inclination on the response of ring footings.This paper aims at studying the behavior of ring footing,resting on unreinforced and/or fiber-reinforced sand beds,when subjected to concentric,eccentric and inclined loadings using FE package PLAXIS 3D.Moreover,by replacing the loose sand up to some depth with compacted randomly distributed fiber-reinforced sand(RDFS)( fibers distributed randomly in the soil to obtain a homogeneous soil fiber mixture),the influence of sand reinforcement on the behavior of ring footing can be studied.Ring footing used in this study has radius ratio(ri/ro)of 0.4,with outer and inner radii of 150 mm and 60 mm,respectively.Fiber percentage and depth of reinforced sand used in this study are 1%and 1B,respectively,whereBis the outer diameter of ring footing.Both parameters are kept constant,because the effect of these parameters on ring footing subjected to concentric loading only has already been documented(Sharma and Kumar,2017a,b).The load eccentricities of 0B,0.05Band 0.1B,and inclinations of 0°,5°,10°,15°,-5°,-10°and-15°,are used in this study.Furthermore,an empirical expression is developed using regression technique which will be useful in plotting loadsettlement curve for eccentric,inclined and/or eccentric-inclined loaded ring footings.Finally,the numerical results are validated with the model plate load test results.
2.Load application,sign conventions and definitions for load inclination and tilting
Fig. 1a shows the sign conventions for measuring the resultant load(Qr)inclination with respect to theZ-axis.Load inclination is positive when it is measured anticlockwise and negative when it is clockwise with respect to theZ-axis,as shown in Fig. 1a.The ratio of difference between settlements at opposite sides to width of the footing is taken as the tilt of the footing(Fig. 1b).
In order to apply vertical loads to the ring footing,uniformly distributed load is converted into multiple closely spaced point loads and then applied in a circular and symmetrical fashion,as shown in Fig. 2.Similarly,load inclination and eccentricities are given to these multiple closely spaced point loads to study their effects on the behaviors of ring footings.
3.Numerical study
Numerical study of ring footings resting on unreinforced and/or fiber-reinforced sand beds is carried out using FE package PLAXIS 3D.The width of the soil bed is taken as five times the footing width,and the depth is taken as three and a half times the footing width.Footing and soil bed model used in the FE analysis is shown in Fig. 3,in whichRD1is the relative density of top RDFS layer,andRD2is the relative density of bottom unreinforced sand layer.
PLAXIS is designed for the two-or three-dimensional analyses of deformation,stability and groundwater fl ow in geotechnical engineering.Geotechnical applications require advanced constitutive models for the simulation of the nonlinear,time-dependent,and anisotropic behaviors of soils and/or rocks.Although the modeling of soil itself is an important issue,many geotechnical projects involve the modeling of structures and the interaction between the structures and the soil.PLAXIS is equipped with features to deal with various aspects of complex geotechnical structures.

Fig. 2.Multiple closely spaced point loads applied on ring footing.

Fig. 1.definitions for(a)load inclination and(b)footing tilt.
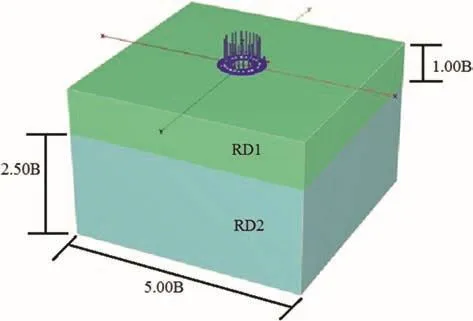
Fig. 3.Footing and soil bed model used in the numerical analysis.
Out of the various constitutive models available in the PLAXIS,the elastic-perfectly plastic Mohr-Coulomb model and non associated flow rule are used in this study.The ring footing has been modeled as rigid plate and is considered to be very stiff and roughin the analysis.Input parameters used in this study(provided by the supplier)for ring footing are presented in Table 1.Various input parameters of unreinforced and fiber-reinforced sands were obtained by conducting drained triaxial shear tests(Sharma and Kumar,2017a)and are presented in Table 2.As fiber reinforcement cannot be modeled directly in PLAXIS,the soil is assumed as cohesive-frictional sand.The term ‘cohesion’in fiber reinforced sand does not correspond to the intermolecular cohesion,but it corresponds to apparent cohesion due to the fact that sand grains adjacent to the fibers are gripped on fiber’s surface.
PLAXIS incorporates fully automatic mesh generation procedure,in which the model is divided into elements of basic type,and compatible structural elements.Five different mesh densities are available in PLAXIS(very coarse,coarse,medium, fine,and very fine).Preliminary trials were carried out on these five mesh densities for footing resting on unreinforced sand(Fig. 4).There was not much significant difference between the medium and fine mesh densities.Hence,the medium mesh density was selected.In areas where large stress concentration or large deformation gradient is expected,it is desirable to have finer element mesh.For this,automatic mesh refinement was done near the edges of foundation.Automatic boundary conditions were applied to the model geometry.PLAXIS generates automatic boundary conditions in which there is fully fixity at the base and smooth condition at the vertical sides.The scheme for the FE analysis is presented in Table 3.
4.Results and discussion
To study the effects of load inclination,eccentricity and fiber reinforcement,a dimensionless term called reduction factor(RF)is introduced,which is defined as the ratio of the ultimate load of an eccentric,inclined or eccentric-inclined loaded foundation(Qu1)tothat of a foundation where applied load is vertical and concentric(Qu2)(Patra et al.,2006;Ornek,2014).Its mathematical form can be written as

Table 1Input parameters for ring footing.

Table 2Input parameters used for loose sand and RDFS.

Fig. 4.Sensitive study of mesh density for ring footing.

Table 3Test scheme.

Table 4Ultimate load(Qu)and RF obtained in the present study.

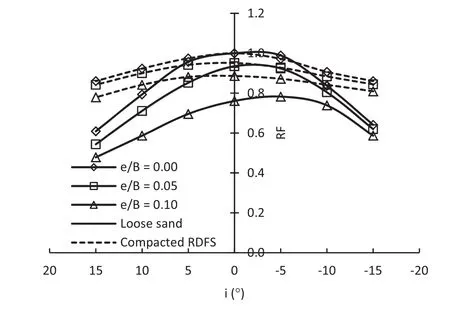
Fig. 5.Effect of load inclination on RF for different eccentricities and sand beds.
The effective area of the ring footing will not be constant as the load eccentricity increases.Therefore,this study emphasizes the load-settlement behavior of ring footing,instead of pressure settlement behavior.Once the ultimate load is known,the ultimate bearing capacity can be calculated easily,if the effective area of ring footing is computed.The ultimate load(Qu)and RF obtained for ring footing are listed in Table 4.
4.1.Effect of load inclination
Fig. 5 shows the effect of load inclination on RF for different eccentricities and sand beds.It can be inferred from Fig. 5 that as the load eccentricity increases,there is a significant change in the RF,whether load inclination is positive or negative.RF values for loose sand are 0.7,0.59 and 0.48 corresponding to load inclinations of 5°,10°and 15°,respectively.Under the same conditions,RF values for compacted RDFS are 0.88,0.84 and 0.78,respectively.Similarly,RF values for loose sand at load inclinations of-5°,-10°and-15°are 0.78,0.74 and 0.59,respectively.Under the same conditions,RF values for RDFS are 0.87,0.84 and 0.81,respectively.It can also be inferred from Fig. 5 that as the loose sand is replaced with compacted RDFS,there is a slight decrease in RF which clearly shows the effect of reinforcement.
Fig. 6a and b shows the effect of load inclination on the ultimate load of ring footing resting on loose sand and compacted RDFS,respectively.It can be inferred from Fig. 6 that as the load inclination increases,there is a significant decrease in the ultimate load of ring footing.At the load inclinations of 5°,10°and 15°,the ultimate loadsQufor loose sand are 3.2 kN,2.7 kN and 2.2 kN,respectively,and those for compacted RDFS are 37.9 kN,36.2 kN and 33.5 kN,respectively.Similarly,at the load inclinations of-5°,-10°and-15°,the ultimate loadsQufor loose sand are 3.6 kN,3.4 kN and 2.7 kN,respectively,and those for compacted RDFS are 37.5 kN,36.2 kN and 34.8 kN,respectively.It can be observed from these values and Fig. 6 that when the load inclination is negative,the ultimate load of footing is larger as compared to its respective positive load inclination(Similar behavior can be inferred from Fig. 5 when RF is concerned).This behavior is due to the fact that as the load inclination is positive,the load is acting away from the center of the footing.Similarly,when the load inclination is negative,the load is acting towards the center.This behavior is more pronounced in loose sand which has been reduced to some extent by the compacted RDFS.
Fig. 7 shows the load-tilt relationship of ring footing for loose sand and compacted RDFS.It can be observed from Fig. 7a and c that as the positive load inclination increases,both for loose sand and compacted RDFS,there is a significant increase in tilt of footing at different load eccentricities.In Fig. 7b,it can be seen that the tilt of footing at load inclination of-5°is smaller than that at 0°.This is due to the same reason that has been explained in the previous paragraph,i.e.when the load inclination is negative,the load is acting towards the center of the footing as compared to the positive load inclination where the load is acting away from the center of the footing.Fig. 7d has not shown this phenomenon which signifies the effect of compacted RDFS.

Fig. 6.Effects of load inclination on ultimate load for(a)loose sand and(b)compacted RDFS.

Fig. 7.Effects of load inclination on tilt of footing for(a,b)loose sand and(c,d)compacted RDFS.
Figs.8 and 9 show the horizontal displacement vectors at ultimate load for loose sand and compacted RDFS,respectively,whene/B=0.1 andi=0°,5°,10°,15°,-5°,-10°and-15°.It can be inferred from Figs.8 and 9 that as the load inclination increases,there is a significant increase in horizontal displacement vector at ultimate load.For loose sand ati=5°,10°and 15°(e/B=0.1),the horizontal displacement vectors at ultimate load are 116.2 mm and-1.09 mm,140.6 mm and-3.55 mm,and 134.6 mm and-4.02 mm,respectively(positive and negative values show the direction of movement of soil particles).Similarly,when the load inclinations are-5°,-10°and-15°,their values are 98.22 mm and-49.74 mm,88.98 mm and-107.9 mm,and 42.6 mm and-155.9 mm,respectively.For the compacted RDFS ati=5°,10°and 15°(e/B=0.1),the horizontal displacement vectors at ultimate load are 463.6 mm and-182.5 mm,697 mm and-105.4 mm,and 1094 mm and-32.13 mm,respectively.Similarly,when the load inclinations are-5°,-10°and-15°,their values are 236.2 mm and-307.7 mm,229.7 mm and-454.7 mm,and 118.9 mm and-418.2 mm,respectively.It can be interpreted from these values that as the load inclination changes from positive to negative,there is a decrease in horizontal displacement of sand in positiveXdirection and minor increase in negativeXdirection.This effect is more significant when sand is loose and unreinforced,and it has been reduced to some extent when sand is replaced with compacted RDFS.
4.2.Effect of load eccentricity
Fig. 10a and b shows the effect of load eccentricity on RF for loose sand and compacted RDFS,respectively.It can be inferred from Fig. 10 that as the load eccentricity increases,RF decreases significantly.Ase/Bchanges from0 to0.05 and then to0.1,RF values for loose sand are obtained as follows:1,0.93 and 0.76(fori=0°);0.96,0.85 and 0.7(fori=5°);and 0.99,0.92 and 0.78(fori=-5°),respectively.Similarly,RF values for compacted RDFS are obtained as follows:1,0.95 and 0.89(fori=0°);0.97,0.94 and 0.88(fori=5°);and 0.97,0.93 and 0.87(fori=-5°),respectively.Similar decreasing phenomenon has been observed for other load inclinations considered in this study.One interesting behavior can be observed from comparison of Fig. 10a with Fig. 10b that as the load eccentricity increases,the decrease in RF is more pronounced in loose sand(Fig. 10a)than that in compacted RDFS(Fig. 10b).This behavior completely justifies the effect of reinforcement on the behavior of eccentrically loaded footing.
Fig. 11a and b shows the effect of load eccentricity on ultimate load of footing resting on loose sand and compacted RDFS,respectively.It can be seen from Fig. 11 that as the load eccentricity increases,there is a significant decrease inQu.Whene/Bchanges from 0 to 0.05 and then to 0.1,Quvalues for loose sand are obtained as follows:4.6 kN,4.3 kN and 3.5 kN(fori=0°);4.4 kN,3.92 kN and 3.2 kN(fori=5°);and 4.55 kN,4.25 kN and 3.6 kN(fori=-5°),respectively.Similarly,Quvalues for compacted RDFS are obtained as follows:43 kN,40.9 kN and 38.1 kN(fori=0°);41.9 kN,40.5 kN and 37.9 kN(fori=5°);and 41.8 kN,39.9 kN and 37.5 kN(fori=-5°),respectively.For other load inclinations,similar decreasing behavior inQuhas been observed.The effect of reinforcement has also been observed by comparing theQuvalues of Fig. 11a with Fig. 11b.
Effect of load eccentricity on tilt of footing can be observed from Fig. 7.One can see that the tilt of footing increases with the load eccentricity.When comparing the load-tilt curves of loose sand(Fig. 7a and b)with those of compacted RDFS(Fig. 7c and d),reinforcement does not show much significant reduction effect on tilt.It can be due to the model selection or input parameters used for reinforcing the sand.
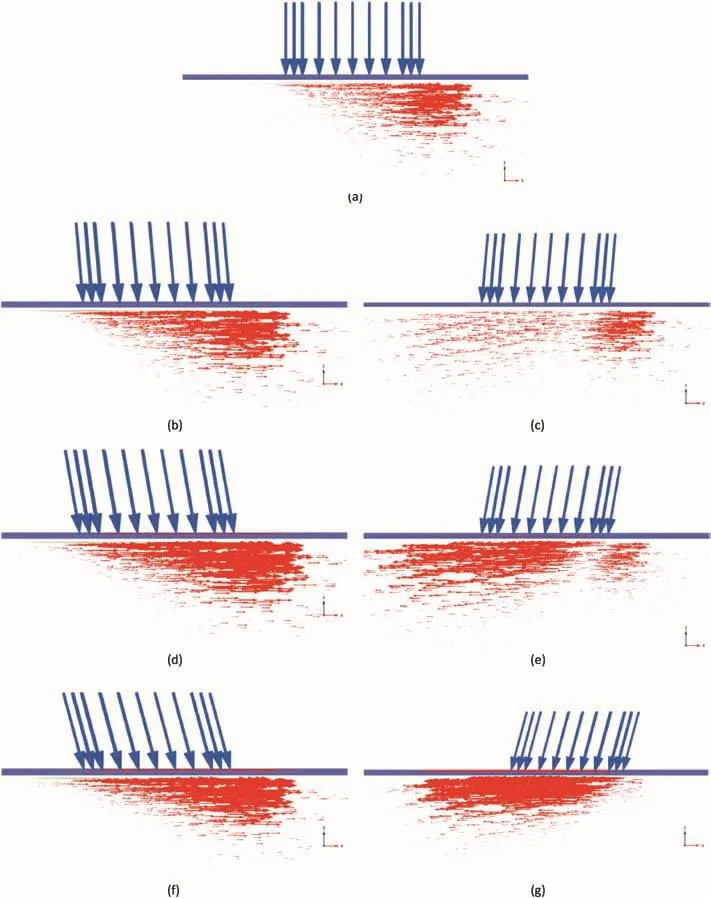
Fig. 8.Horizontal displacement vectors at ultimate load for loose sand at e/B=0.1 and(a)i=0°,(b)i=5°,(c)i=-5°,(d)i=10°,(e)i=-10°,(f)i=15°,and(g)i=-15°.
Figs.12a and b,8f and g show the effects of load eccentricity on horizontal displacement vectors at ultimate load for loose sand.Similarly,Figs.12c and d,9f and g show the effects of load eccentricity on horizontal displacement vectors at ultimate load for compacted RDFS.It can be inferred from these figures that as the load eccentricity increases,the horizontal displacement vectors at ultimate load increase.Wheni=15°for loose sand,the horizontal displacement vectors at ultimate load fore/B=0.05 and 0.1 are 121.4 mm and-17.09 mm,and 134.6 mm and-4.02 mm,respectively.Wheni=-15°for loose sand,the horizontal displacement vectors at ultimate load fore/B=0.05 and 0.1 are 44.32 mm and-165.6 mm,and 42.6 mm and-155.9 mm,respectively.Wheni=15°for compacted RDFS,the horizontal displacement vectors at ultimate load fore/B=0.05 and 0.1 are 752.7 mm and-24.1 mm,and 1094 mm and-32.13 mm,respectively.Wheni=-15°for compacted RDFS,the horizontal displacement vectors at ultimate load fore/B=0.05 and 0.1 are 21.4 mm and-481.9 mm,and 118.9 mm and-418.2 mm,respectively.
4.3.Regression analysis
The load-settlement curves for footing under consideration can be plotted using PLAXIS 3D.If the software is not available,the load-settlement curves for the footing used in this study can be plotted by using Eq.(2),which is developed using regression analysis on the load-settlement data obtained from the FE analysis of ring footing by considering all of the vital bearing capacity parameters.

whereQis the load corresponding to settlement(S),QsandSare respectively the load and settlement of loose sand under central point loading without inclination.The coefficient of determination(R2)is found to be 0.9779 for Eq.(2).Fig. 13 illustrates a typical graph of observed versus predicted data of ultimate load of ring footing resting on loose sand and compacted RDFS.
Regression analysis is one of the available empirical estimation methods which are common in civil engineering(Bera et al.,2005).In this technique,a function is assumed to estimate the relationship between the independent and dependent variables.The coefficients of the assumed function are determined by the least square method using observed data.A general linear model is assumed in the following form:


Fig. 9.Horizontal displacement vectors at ultimate load for compacted RDFS at e/B=0.1 and(a)i=0°,(b)i=5°,(c)i=-5°,(d)i=10°,(e)i=-10°,(f)i=15°,and(g)i=-15°.
whereyis the dependent variable;x1,x2,…,xpare the independent variables; ξ1,ξ2,…,ξpare the unknown parameters;andpis the number of independent variables.
In real practice,nobservations would be available onywith correspondingnobservations on each of thepindependent variables.Thennumbers of equations are written as

whereykis thekth observation onyandxklis thekth observation on thelth independent variable.Eq.(4)can be rewritten as


Fig. 10.Effects of load eccentricity on RF for(a)loose sand and(b)compacted RDFS.

Fig. 11.Effects of load eccentricity on ultimate load of footing resting on(a)loose sand and(b)compacted RDFS.

Fig. 12.Effects of load eccentricity on horizontal displacement vectors at ultimate load for(a,c)loose sand with i=15° and-15°,respectively,and(b,d)compacted RDFS with i=15° and-15°,respectively(e/B=0.05).

where y is then1 vector of observations,x is a matrix(np)made up of observations on each ofpindependent variables,andξ is thep1 vector of unknown parameters.To have an intercept term in Eq.(6),it is necessary thatxi1=1,whileξ1becomes the intercept.
The selection of an appropriate model highly depends on the judgment of the researchers,including incorporation of relevant theory and knowledge of the subject under consideration,and careful examination of scatter plots,residual plots and regression diagnostics(Dielman,2001).Partial information about the relationship between dependent and independent variables can be obtained by forming a scatter plots matrix(Dielman,2001).In the present study,a nonlinear power model is chosen,on the basis of the scatter plots matrix,and can be written as

This nonlinear regression model can be transformed into linear model by using a logarithmic transformation as

Analyzing the scatter plot matrix obtained from the FE data,a nonlinear power model has been chosen as

Eq.(9)can be transformed to a linear equation by taking logarithm on both sides so that standard regression techniques can be used.The transformed linear equation can be expressed as

After applying standard regression techniques,all the unknown parameters(ξ0,ξ1,ξ3,…,ξ6)can be obtained and can be referred to Eq.(2).
5.Comparison with the model plate load tests
In order to validate the numerical findings,some laboratory model plate load tests were performed.The model tests were carried out on both unreinforced and fiber-reinforced sands with eccentric loading(e/B=0,0.05 and 0.1).The testing tank was 1.5 m wide,1.5 m long and 1 m deep.Model footing was made up of mild steel with internal and external diameters of 0.12 m and 0.3 m,respectively.Detailed information about the testing assembly and sample preparation for model plate load test can refer to Sharma and Kumar(2017b).The load-settlement curves obtained from model plate load tests are shown in Fig. 14.Fig. 15 shows the comparison of numerical findings with model plate load test results.It can be inferred from Fig. 15 that there is a good agreement between the numerical and model test results which validates the numerical findings of this study.
6.Scale effect
PLAXIS 3D software has been used to study the scale effect of model footing resting on fiber-reinforced sand.Model footings,with various sizes(outer diameter of model footing,Bp),used in the analysis are 30 cm,45 cm,60 cm and 75 cm.Similarly,prototype foundations,with various sizes(outer diameter of prototype foundation,Bf),used in the analysis are 100 cm,210 cm,300 cm and 400 cm.Depending on the sizes of model/prototype footings,the size of soil mass has been modified accordingly.Thicknesses of model footings and prototype foundations,and tank dimensions have also been modified on the basis of their scale modification.The horizontal and vertical extents of the tank are taken as 5Band 3.5B,respectively.Other parameters such as unit weight,Poisson’s ratio and Young’s modulus of model footings and prototype foundations are kept constant,as listed in Table 1.

Fig. 14.Load-settlement curves for model plate load tests.
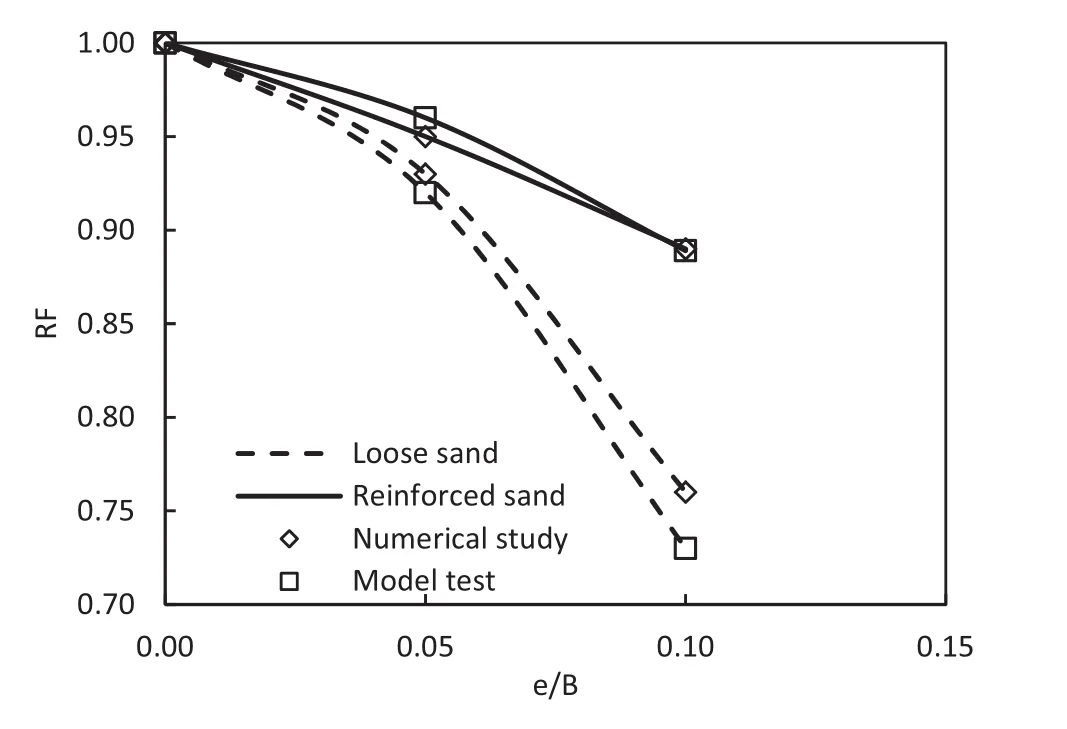
Fig. 15.Comparison of numerical and experimental results.
Two dimensionless factors have been developed using regression analysis and are described along with their equations as

whereQf/Qpis the load factor defined as the ratio of load acting on prototype foundation to that acting on model footing,Sf/Spis the settlement factor defined as the ratio of settlement corresponding to the load acting on prototype foundation to that corresponding to load acting on model footing,h1is the thickness of top fiber-reinforced sand layer,andFcis the percentage of fibers in the sand(1%in this study).The coefficients of determination(R2)for Eqs.(11)and(12)are 0.971 and 0.965,respectively.
In this study,RD1will be the same asRD2when studying footing resting on loose unreinforced sand.RD1will become 70%andRD2will be 30%when studying footing resting on RDFS layer overlying unreinforced sand.Bothh1/BandFcwill be taken as 0 for footing resting on loose unreinforced sand and 1 for footing resting on RDFS layer overlying unreinforced sand.
7.Conclusions
An effort has been made to study the effects of load inclination and eccentricity on the behavior of ring footing resting on unreinforced and/or fiber-reinforced sands.A numerical approach has been advised to model fiber-reinforced sand.Moreover,numerical results of this study have been compared with the model plate load test results and the following conclusions can be drawn from this study:
(1)As the load inclination increases from 0°to 15°,the ultimate load of footing resting on loose sand is reduced by 41%-52%.Similarly,this reduction is in the range of 19%-22%when footing is resting on RDFS layer overlying unreinforced sand.
(2)As the load eccentricity(e/B)increases from 0 to 0.1,the ultimate load of footing resting on loose sand is reduced by 36%-52%.Similarly,this reduction is in the range of 14%-22%when footing is resting on RDFS layer overlying unreinforced sand.
(3)It has been interpreted from the horizontal displacement vectors at ultimate load that as the load inclination changes from positive to negative,there is a decrease in horizontal displacement of sand in positiveXdirection and minor increase in negativeXdirection.This effect is more significant when sand is loose and unreinforced,and it has been reduced to some extent when sand is replaced with compacted RDFS.
(4)When the load inclination is negative,the RF andQuof footing are larger as compared to those at its respective positive load inclination,especially when the load inclination changes from 5°to-5°.This behavior is due to the fact that as the load inclination is positive,the load is acting away from the center of the footing.
(5)Comparing the effect of load eccentricity on RF for loose sand and compacted RDFS shows that as the load eccentricity increases,the decrease in RF is more pronounced in loose sand than that in compacted RDFS.This behavior completely justifies the effect of reinforcement on the behavior of eccentrically loaded footing.
(6)An empirical expression obtained using regression analysis can be adopted to plot the load-settlement curve for ring footing(for any condition used in the present study),if the load-settlement data of ring footing resting on loose sand with central point load are available.
Conflict of interest
The authors wish to confirm that there are no known Conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
Al-Sanad HA,Ismael NF,Brenner RP.Settlement of circular and ring plates in very dense calcareous sands.Journal of Geotechnical Engineering 1993;119(4):622-38.
Badakhshan E,Noorzad A.Load eccentricity effects on behavior of circular footings reinforced with geogrid sheets.Journal of Rock Mechanics and Geotechnical Engineering 2015;7(6):691-9.
Badakhshan E,Noorzad A.Effect of footing shape and load eccentricity on behavior of geosynthetic reinforced sand bed.Geotextilesand Geomembranes 2017a;45(2):58-67.
Badakhshan E,Noorzad A.A simplif i ed method for prediction of ultimate bearing capacity of eccentrically loaded foundation on geogrid reinforced sand bed.International Journal of Geosynthetics and Ground Engineering 2017b;3(2):1-15.
Behera RN,Patra CR,Sivakugan N,Das BM.Prediction of ultimate bearing capacity of eccentrically inclined loaded strip footing by ANN-part II.International Journal of Geotechnical Engineering 2013;7(2):165-72.
Benmebarek S,Remadna MS,Benmebarek N,Belounar L.Numerical evaluation of the bearing capacity factorN′γ of ring footings.Computers and Geotechnics 2012;44:132-8.
Bera AK,Ghosh A,Ghosh A.Regression model for bearing capacity of a square footing on reinforced pond ash.Geotextiles and Geomembranes 2005;23(3):261-85.
Boushehrian JH,Hataf N.Experimental and numerical investigation of the bearing capacity of model circular and ring footings on reinforced sand.Geotextiles and Geomembranes 2003;21(4):241-56.
Bowles JE.Elastic foundation settlements on sand deposits.Journal of Geotechnical Engineering 1987;113(8):846-60.
Dielman TE.Applied regression analysis for business and economics.Duxbury,USA:Thomson Learning,Inc.;2001.
El Sawwaf MA.Behavior of strip footing on geogrid-reinforced sand over a soft clay slope.Geotextiles and Geomembranes 2007;25(1):50-60.
El Sawwaf M.Experimental and numerical study of eccentrically loaded strip footings resting on reinforced sand.Journal of Geotechnical and Geoenvironmental Engineering 2009;135(10):1509-18.
El Sawwaf M,Nazir A.Behavior of eccentrically loaded small-scale ring footings resting on reinforced layered soil.Journal of Geotechnical and Geoenvironmental Engineering 2012;138(3):376-84.
Hjiaj M,Lyamin AV,Sloan SW.Bearing capacity of a cohesive-frictional soil undernoneccentric inclined loading.Computers and Geotechnics 2004;31(6):491-516.
Ismael NF.Loading tests on circular and ring plates in very dense cemented sands.Journal of Geotechnical Engineering 1996;122(4):281-7.
Jao M,Ahmed F,Muninarayana G,Wang MC.Stability of eccentrically loaded footings on slopes.Geomechanics and Geoengineering 2008;3(2):107-11.
Keshavarz A,Kumar J.Bearing capacity computation for a ring foundation using the stress characteristics method.Computers and Geotechnics 2017;89:33-42.
Kumar J,Chakraborty M.Bearing capacity factors for ring foundations.Journal of Geotechnical and Geoenvironmental Engineering 2015;141(10).https://doi.org/10.1061/(ASCE)GT.1943-5606.0001345.
Kumar J,Ghosh P.Bearing capacity factorNγfor ring footings using the method of characteristics.Canadian Geotechnical Journal 2005;42(5):1474-84.
Laman M,Yildiz A.Model studies of ring foundations on geogrid-reinforced sand.Geosynthetics International 2003;10(5):142-52.
Laman M,Yildiz A.Numerical studies of ring foundations on geogrid-reinforced sand.Geosynthetics International 2007;14(2):52-64.
Lee J,Eun J.Estimation of bearing capacity for multiple footings in sand.Computers and Geotechnics 2009;36(6):1000-8.
Lee JK,Jeong S,Lee S.Undrained bearing capacity factors for ring footings in heterogeneous soil.Computers and Geotechnics 2016;75:103-11.
Meyerhof GG,Hanna AM.Ultimate bearing capacity of foundations on layered soil sunder inclined load.Canadian Geotechnical Journal1978;15(4):565-72.
Naderi E,Hataf N.Model testing and numerical investigation of interference effect of closely spaced ring and circular footings on reinforced sand.Geotextiles and Geomembranes 2014;42(3):191-200.
Naseri M,Hosseininia ES.Elastic settlement of ring foundations.Soils and Foundations 2015;55(2):284-95.
Ornek M.Estimation of ultimate loads of eccentric-inclined loaded strip footings rested on sandy soils.Neural Computing and Applications 2014;25(1):39-54.Patra CR,Das BM,Bhoi M,Shin EC.Eccentrically loaded strip foundation on geogridreinforced sand.Geotextiles and Geomembranes 2006;24(4):254-9.
Saran S,Agarwal RK.Eccentrically-obliquely loaded footing.Journal of Geotechnical Engineering 1989;115(11):1673-80.
Saran S,Agarwal RK.Bearing capacity of eccentrically obliquely loaded footing.Journal of Geotechnical Engineering 1991;117(11).1669-9.
Saran S,Kumar S,Garg KG,Kumar A.Analysis of square and rectangular footings subjected to eccentric-inclined load resting on reinforced sand.Geotechnican and Geological Engineering 2007;25(1):123-37.
Sastry VVRN,Meyerhof GG.Inclination factors for strip footings.Journal of Geotechnical Engineering 1987;113(5):524-7.
Sharma V,Kumar A.Strength and bearing capacity of ring footings resting on fibre reinforced sand.International Journal of Geosynthetics and Ground Engineering 2017a;3:1-17.https://doi.org/10.1007/s40891-017-0086-6.
Sharma V,Kumar A.influence of relative density of soil on performance of fiber reinforced soil foundations.Geotextiles and Geomembranes 2017b;45(5):499-507.https://doi.org/10.1016/j.geotexmem.2017.06.004.
Taiebat HA,Carter JP.Bearing capacity of strip and circular foundations on undrained clay subjected to eccentric loads.Géotechnique 2002;52(1):61-4.
Zhao L,Wang JH.Vertical bearing capacity for ring footings.Computers and Geotechnics 2008;35(2):292-304.
 Journal of Rock Mechanics and Geotechnical Engineering2018年2期
Journal of Rock Mechanics and Geotechnical Engineering2018年2期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Behavior of diatomaceous soil in lacustrine deposits of Bogotá,Colombia
- Resilient modulus prediction of soft low-plasticity Piedmont residual soil using dynamic cone penetrometer
- Assessment of natural frequency of installed offshore wind turbines using nonlinear finite element model considering soil-monopile interaction
- A new design equation for drained stability of conical slopes in cohesive-frictional soils
- Investigation of active vibration drilling using acoustic emission and cutting size analysis
- Numerical analysis of Shiobara hydro power cavern using practical equivalent approach
