基于自适应动态无偏最小二乘支持向量机的刀具磨损预测建模

肖鹏飞 张超勇 罗 敏 林文文

1.华中科技大学机械科学与工程学院，武汉，4300742.宁波大学机械工程与力学学院，宁波，315211

0 引言

刀具在切削过程中会逐渐磨损退化直至失效，刀具在初期磨损、正常磨损到严重磨损直至失效过程中将不同程度地降低产品质量，甚至会损坏机床，影响加工系统运行，造成重大损失[1]。统计研究表明:采用刀具监测技术可以有效缩短停机时间，显著提高生产率和机床利用率；实时监测刀具状态不但延长了刀具自身的使用时间，而且还能有效防范刀具失效造成的工件报废和机床故障，进而削减成本[2]。

根据测量手段的不同，刀具状态监测方法主要分为直接法和间接法。直接法较常见的有接触测量法和机器视觉图像测量法[3],直接法因监测过程的高成本和不协调而在加工领域的应用受到限制。间接法通过利用刀具磨损间接相关的信号进行监测，可在不中断加工过程的情况下实现在线监测，非常适合自动加工系统，受到越来越多的关注。切削加工进程中的许多特征都可用于判别刀具的状态，如刀具和主轴振动所发出的声音和振幅信号，切削力、切削温度、主轴功率或扭矩的实时变化，以及声发射信号等。在间接监测方法中，刀具磨损监测系统的组成主要包括研究对象(刀具)、加工条件、传感器检测、信号处理、特征信号提取与选择以及磨损量预测等模块和环节。

张臣等[4]研究表明，与前向神经网络方法相比，采用最小二乘支持向量机(least square support vector machine，LSSVM)构建监测模型所得到的监测结果更加准确。VIJAYAKUMAR[5]在标准支持向量机结构风险的置信范围中添加了b2/λ2(λ>0)项，提高学习速度的同时，对泛化能力的影响不大。由于训练样本数量有限，以及滑动时间窗长度和监测模型不能自适应调整和更新等因素，传统基于机器学习的刀具磨损预测模型存在精度和效率较低等问题，本文在满足预测精度要求的基础上引入了滑动时间窗长度自适应确定算法，提高了数据集长度的自适应性，构建的动态无偏最小二乘支持向量机(dynamic non-bias least square support vector machine，DNLSSVM)在设计上消除偏置项，增加训练样本动态增减过程，有效利用核扩展矩阵对称正定性质，简化动态学习过程中Lagrange乘子的求解，从而提高了建模效率。

1 自适应动态无偏最小二乘支持向量机

1.1 建立初始预测模型

首先利用滑动时间窗内的初始训练数据集建立初始预测模型[6]：设长度为l，则初始训练数据集的形式为{(xi,yi)}(i=1,2,…,l)，其中输入数据xi∈Rn，输出数据yi∈R。在最小二乘支持向量机结构风险的置信范围中添加b2/(2λ2)(λ>0)项，该模型的目标函数和约束条件为

(1)

i=1,2,…,l

令ω′=(ω;b/λ)，则式(1)变成

(2)

i=1,2,…,l

式中,φ(·)为非线性映射函数，它将数据集从输入空间映射到特征空间；b为线性拟合模型的偏置项，参与决定超平面到原点之间的距离；ξ为拟合误差变量；C为针对拟合误差的惩罚因子，C越大，则目标函数对拟合误差的容忍度越小；λ为为了消除偏置b而引入的参数，取较大值会更近似原模型，但值太大又会影响学习过程中的收敛速度和稳定性。

为快速求解上述问题，采用Lagrange乘子法，建立Lagrange函数并利用KKT条件把约束优化问题转变成函数优化问题，解得

(3)

式中，αi为Lagrange乘子。

对于i=1,2,…,l，消去ω′、ξi，并将式(3)写成矩阵形式，即

(K+λ2E+C-1I)α=Y

(4)

Kij=(φ(xi)·φ(xj))=k(xi,xj)K=[Kij]

Y=(y1,y2,…,yl)Tα=(α1,α2,…,αl)T

式中，E为l阶全一方阵；I为l阶单位方阵。

初始预测模型的形式为

(5)

由式(5)可以看出，通过引入参数λ消除了回归函数中的偏置项。

令H=K+λ2E+C-1I(λ>0,C>0)，式(4)简化为Hα=Y，称H为核扩展矩阵，可以证明其为对称正定。H为对称正定矩阵，能够进行Cholesky分解，可以被唯一地分解为H=UTU，其中U为上三角阵。由UTUα=Y，设P=Uα，则UTP=Y。初始预测模型的Lagrange乘子向量α的求取公式为

(6)

(7)

式中，Pi、αi分别为P和α的第i个分量;uik为矩阵U的第i行、第k列元素。

如果通过求H的逆矩阵进而求解Lagrange乘子，则H维度很大时计算复杂，而利用上述公式可以简化计算过程。

1.2 动态更新模型

设t时刻滑动时间窗中有l个样本[7]，则该时刻训练数据集的形式为{(xi,yi)}(i=t+1,t+2,…,t+l)。t+1时刻进来一个新样本(xt+l+1,yt+l+1)，同时淘汰时间窗中该时刻最早的旧样本(xt+1,yt+1)。

在线训练算法中，核函数矩阵K、训练样本输出Y和待求的Lagrange 乘子α都是t的函数，表示如下：

Y(t)=(yt+1,yt+2,…,yt+l)T

(8)

α(t)=(αt+1,αt+2,…,αt+l)T

(9)

Kij(t)=k(xi,xj)

(10)

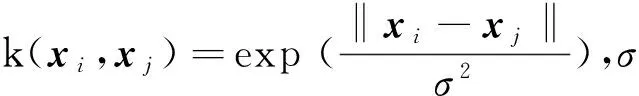
(11)

H(t)为动态正定矩阵，能够进行Cholesky分解。由

K(t)=

(12)

相应地

H(t)=

(13)

由t时刻的学习结果，令H(t)=U(t)TU(t)。t+1时刻增加新样本(xt+l+1,yt+l+1)后，对应H(t)有

(14)

V(t+1)=[k(xt+l+1,xt+1)+λ2

k(xt+l+1,xt+2)+λ2…k(xt+l+1,xt+l)+λ2]T

v(t+1)=k(xt+l+1,xt+l+1)+λ2+C-1

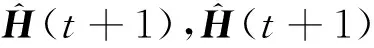
(15)

1.3 自适应计算训练数据集长度算法

一般情况下，用于储存训练数据的滑动时间窗过短可能会导致信息不全和模型精度不高，过长又会导致过拟合和建模速度慢，因此本文采用自适应的时间窗长度选取算法，综合构建自适应动态无偏最小二乘支持向量机(adaptive dynamic non-bias least square support vector machine，ADNLSSVM)。

损失函数Qt-1的计算公式如下:

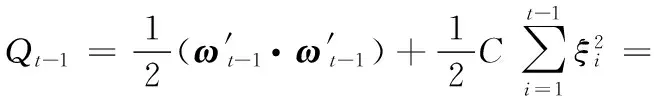
(16)

令Qt-2=Qt-1/l，则损失函数相对下降量

(17)

滑动时间窗的调整需要预先设定预测误差阈值θ和目标函数相对下降量阈值ε，在初始时间窗中，不断添加新的样本建立动态模型，并预测下一样本输出值，在模型预测误差小于阈值θ的情况下，如果连续迭代m次目标函数相对下降量Δt-1均不超过阈值ε，则满足迭代终止条件[6]，如图1所示。

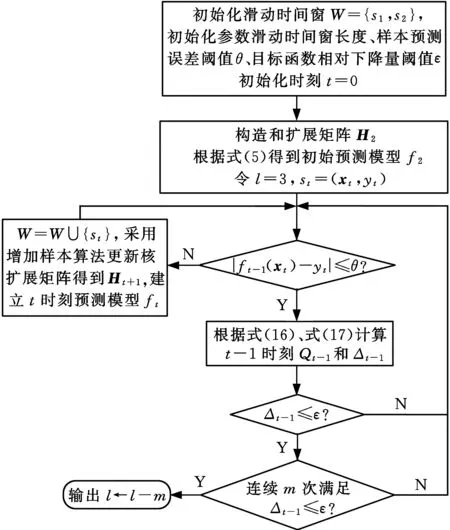
图1 滑动时间窗自适应选取算法流程图Fig.1 Algorithm of adaptively selecting the lengthof sliding time window

2 数据分析与处理

2.1 数据分析

本文采用美国纽约预测与健康管理学会(PHM)2010年高速数控机床刀具健康预测竞赛开放数据中的铣削实验数据[8]进行试验，试验的系统结构和主要设备如图2所示。铣削试验用到的主要设备和试验条件见表1。

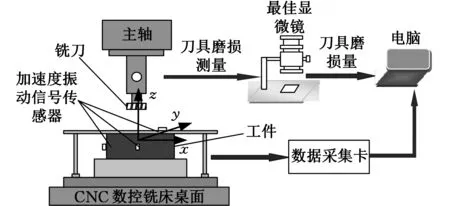
图2 试验系统结构和设备Fig.2 Structure and devices of the experimental system

记每一次走刀过程为108 mm长度的端面铣，由于端面铣加工材料为正方形，刀具每一次走刀时间间隔相等，因此可以用走刀数来代替切削时间，每次走刀后采用LEICA MZ12显微镜测量刀具实际的后刀面磨损量作为刀具磨损结果，一次走刀为一个监测过程。

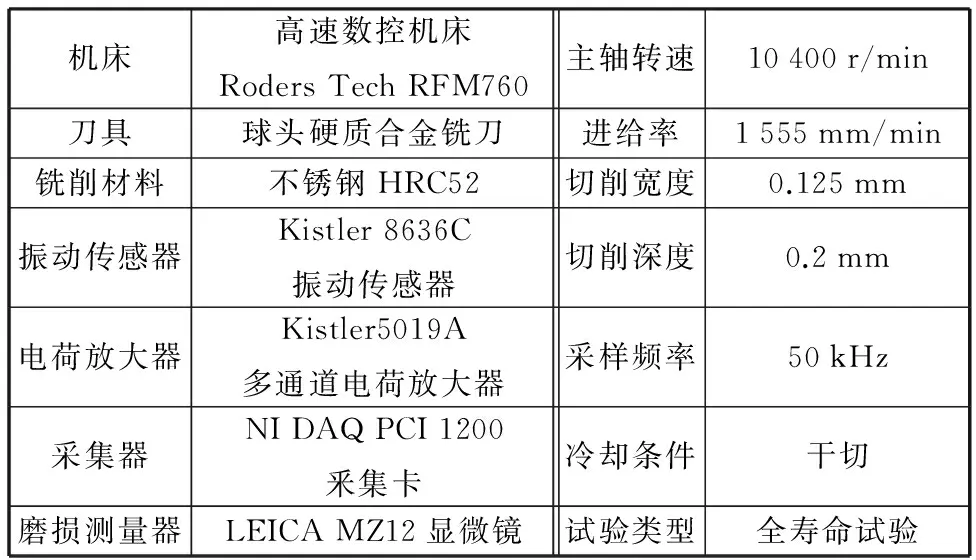
表1 铣削试验主要设备和试验条件Tab.1 Main equipments and machining conditions ofmilling experiment

试验釆用6把独立的铣刀(C1号铣刀～C6号铣刀)进行刀具全寿命试验。下面以C4组铣削试验作为研究对象，该组数据记录了315次走刀试验的振动信号和对应三列磨损数据值，分别表示球头铣刀三个切削刃的磨损量，本文采用三个切削刃磨损量的均值表示铣刀磨损量大小。图3绘出了刀具三个切削刃磨损均值的变化曲线。

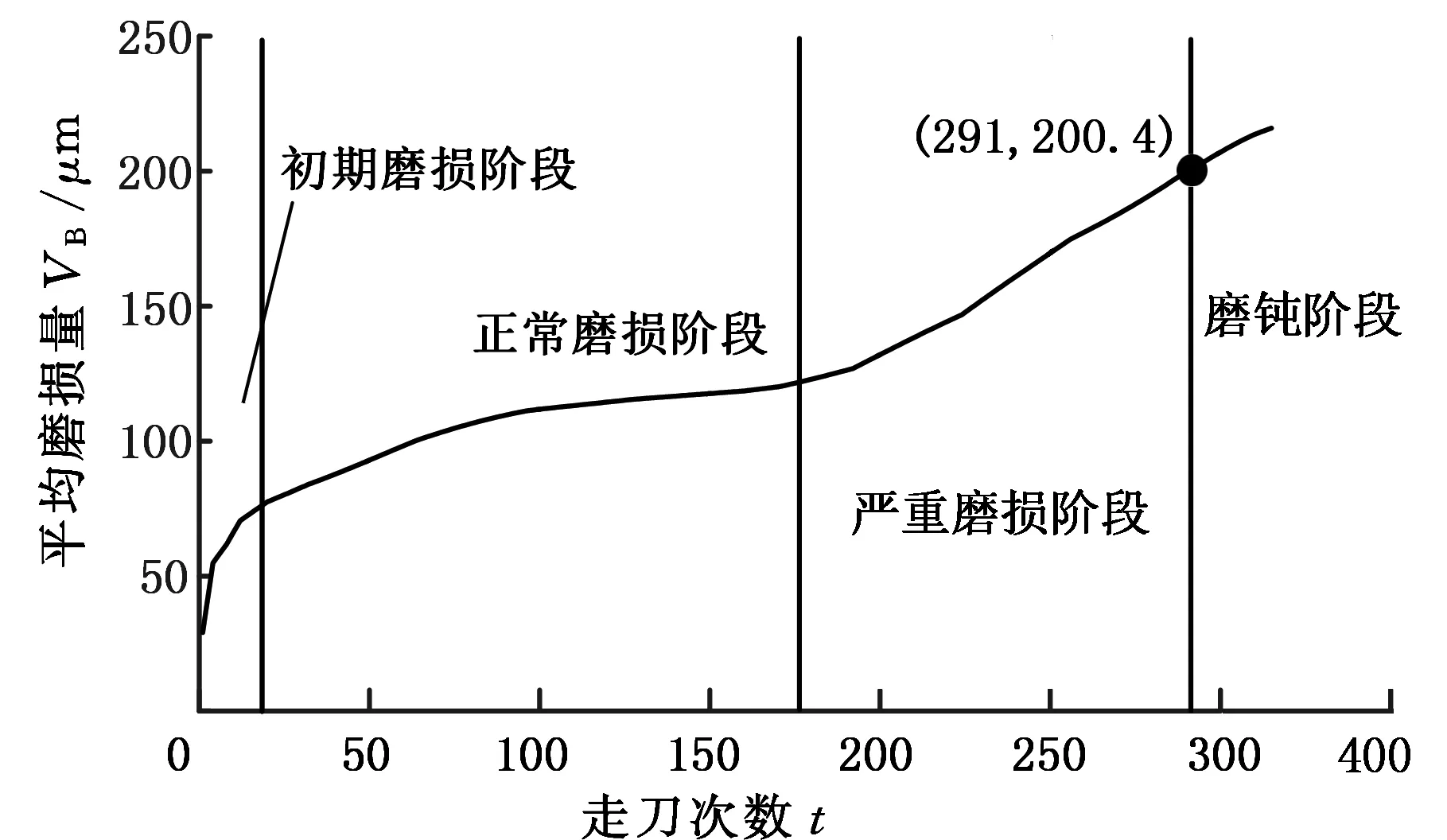
图3 刀具磨损曲线Fig.3 The curve of tool wear amount

由图3可以发现，1～19次走刀曲线较陡，磨损量上升较快后趋于平缓，该阶段内铣刀处于初期磨损阶段；20～176次走刀铣刀磨损量上升过程相对较慢，处于正常磨损阶段；177次走刀以后刀具磨损速度急剧增加，进入急剧磨损阶段，磨损量超过阈值便磨钝失效了[9]。

2.2 铣削振动信号的小波降噪

首先对信号进行零均值化和去除趋势项的预处理。

依据分类情况，为了增强信号的对比度，在三类磨损状态中分别选取第1、第158和第315次的三向振动信号进行分析，其对应的磨损量分别为24.2 μm、95.3 μm、203.1 μm。对这三次走刀过程中各方向(X、Y、Z)铣削振动信号进行频谱分析，按照小波包分解理论[10]，滤除高频噪声，其中,X方向降噪前后频域图见图4。

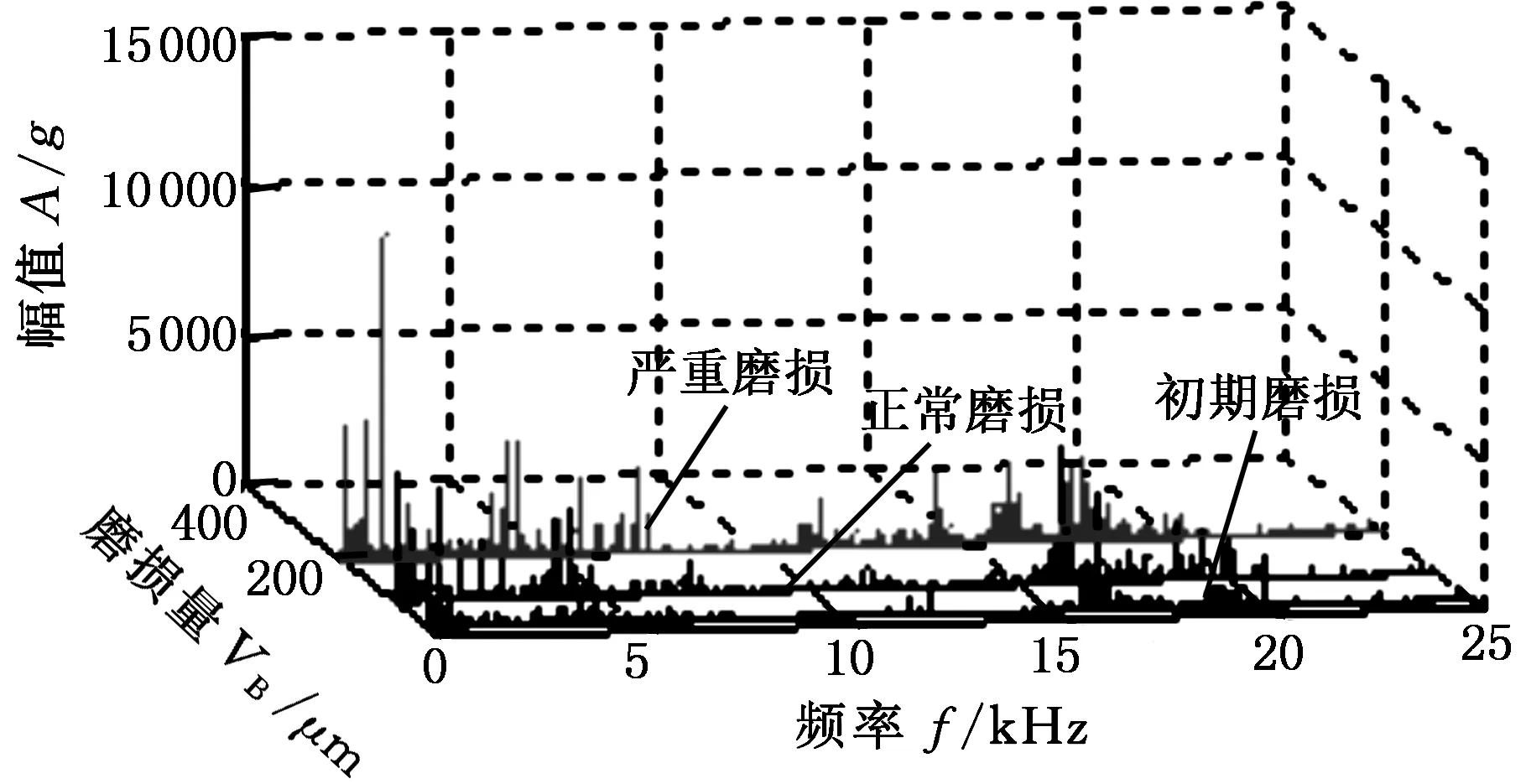
(a)降噪前

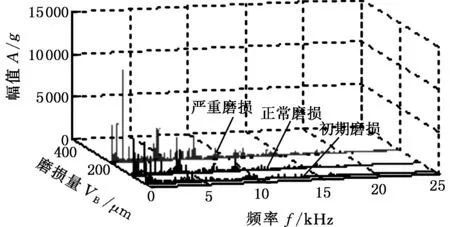
(b)降噪后图4 X方向降噪前后分类频域图Fig.4 The frequency-domain magnitude before andafter denoising in X direction

其他方向铣削信号的降噪处理采用相同的方法完成。

2.3 特征提取

运用时域分析、频域分析及小波时频域分析方法对切削过程的切削振动信号进行分析处理，把振动信号中能够直接有效反映刀具态变化的监测特征抽取并选择出来。

2.3.1时域特征提取

(1)时域有量纲特征。有量纲特征参数以数值形式直观反映振动信号的时域统计特性，计算简单快捷，便于在线实时处理，对刀具磨损和破损等严重切削故障较为敏感，是对振动信号最简单的时域描述，如均值、标准差、均方根值等统计量。

(2)时域量纲一特征。时域有量纲特征是统计量，需要较多的历史数据，而且受加工材料、切削参数等工况条件的影响，没有统一的衡量标准；量纲一特征能在一定程度上克服有量纲特征的这些缺点；两个具有相同量纲的量的比值组成量纲一特征参数，这些参数对信号的幅值和频率变化不敏感，对故障缺陷敏感[8]，如峰值因子、峭度指标、偏度指标等。

图5绘出了铣削振动信号(X方向)的时域有量纲和量纲一参数与刀具磨损量间的变化关系。由图5可知：振动信号的均值在零附近波动，逐渐接近于零，直观上与磨损量无相关性(相关系数为0.129 0)；铣削振动信号的标准差与均方根特征相关性好(相关系数分别为0.922 4、0.921 9)，随着磨损量的增加而递增；量纲一参数中，偏度指标与磨损量的相关性好(相关系数为0.716 2)，其他两个指标与刀具磨损量基本不相关(相关系数分别为0.344 5、0.441 1)。

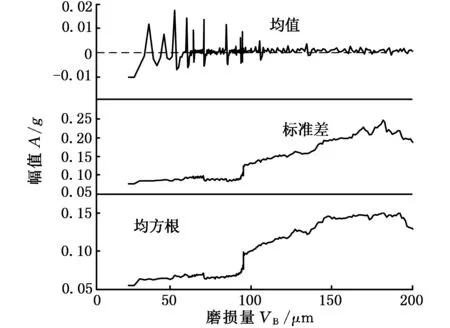
(a)有量纲

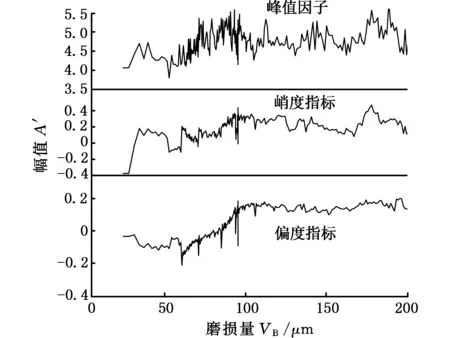
(b)量纲一图5 时域有量纲和量纲一参数变化图Fig.5 The variation curves of features of dimension and non-dimension in time-domain

2.3.2频域特征提取

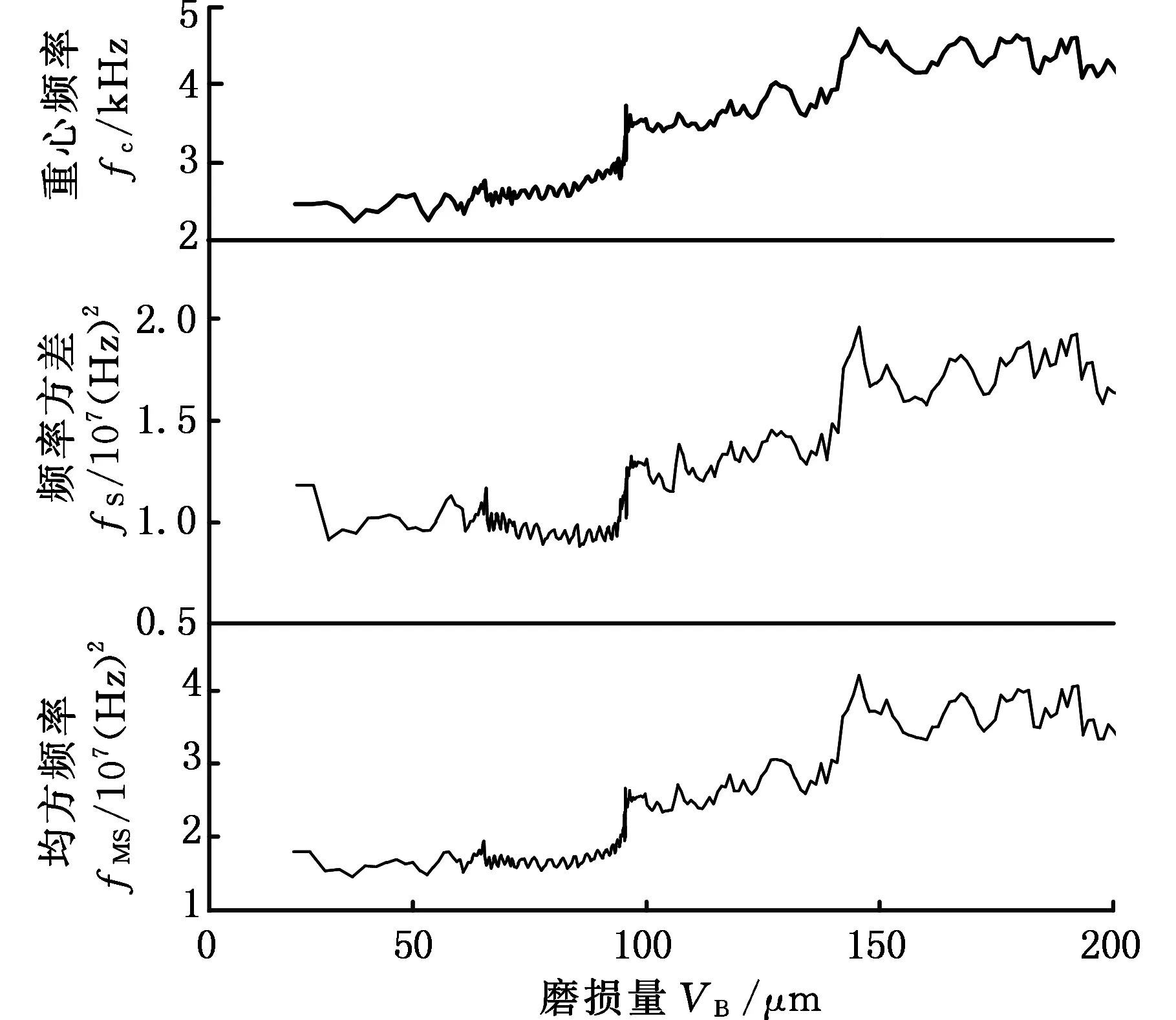
图6 频域特征参数变化图Fig.6 The variation curves of features in frequency-domain

信号的功率谱能很好地揭示刀具运行过程中切削振动频率成分变化的动态信息，被广泛应用于刀具磨损状态监测。常用的谱特征获取方法有相关图法功率谱估计、周期图法功率谱估计。频域特征参数有频段能量、重心频率、频率方差和均方频率等。本文釆用周期图功率谱估计法对铣削监测信号进行功率谱估计，然后计算其频域特征参数。图6所示为X向切削振动信号的频域特征参数随刀具磨损量变化情况。由图6可知：铣削振动频率特征参数随刀具磨损量的增大总体呈上升趋势，但具有波动性。

2.3.3时频域提取

本节分析和提取小波包频带能量与小波熵特征。先对釆样信号进行频谱分析以确定小波包分解的层次。分析得知：不同磨损状态下信号频谱规律性较强，频谱图中各峰值频率呈倍频关系；进行小波包分解时，频带分辨率应不大于518 Hz。由采样频率50 kHz，可以确定进行6层小波包分解。小波包分解层次可以依据以下公式求得[10]：

fmin=Fs/2n+1

(18)

式中，Fs为采样频率;n为层数;fmin为最小频段。

由于铣削振动频率主要集中在1～10 kHz范围内，故应取前32频带(1～12.51kHz)能量作为监测特征。

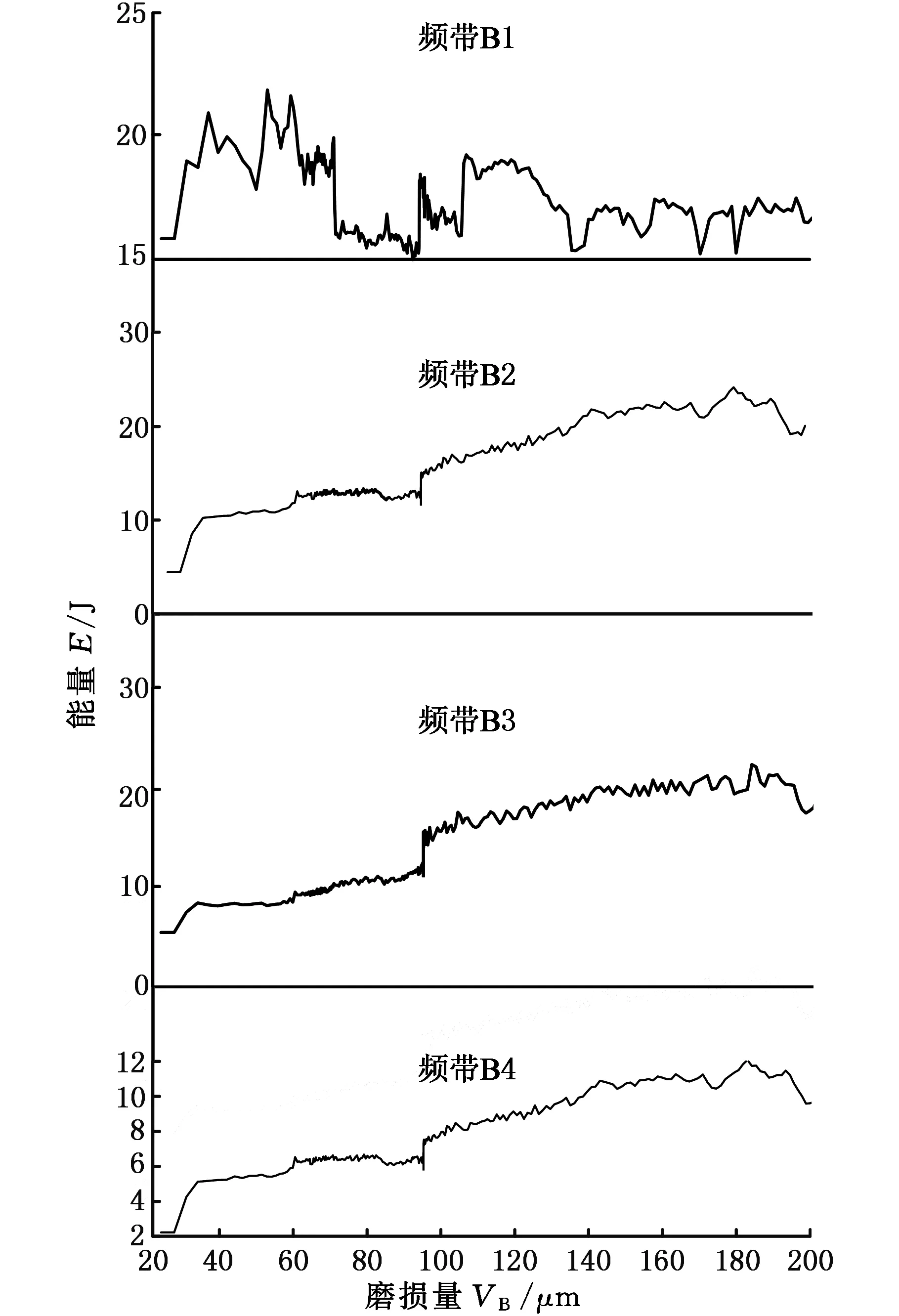
图7列举了铣削X方向振动信号小波包分解的1～4频带能量。由图7可知：铣削振动信号的部分频带能量特征相关性好，小波包频带能量熵能反映刀具磨损状态的变化。铣削振动小波能谱熵与磨损量的相关性比较好。

2.4 特征选择

特征与磨损量之间的相关程度不尽相同并且特征之间也可能有某种关系，这会造成不必要的计算负担和冗余。本文通过相关性分析即分析特征和磨损量间的关系紧密程度，从而识别并挑选出与磨损量相关程度更高的特征作为模型输入，提高建模效果。相关性研究方法包括灰色关联度分析法和相关系数法。

2.4.1相关系数法

用相关系数ρxy衡量两个数据序列X和Y之间的线性相关性，计算公式如下：

(a)部分频带能量

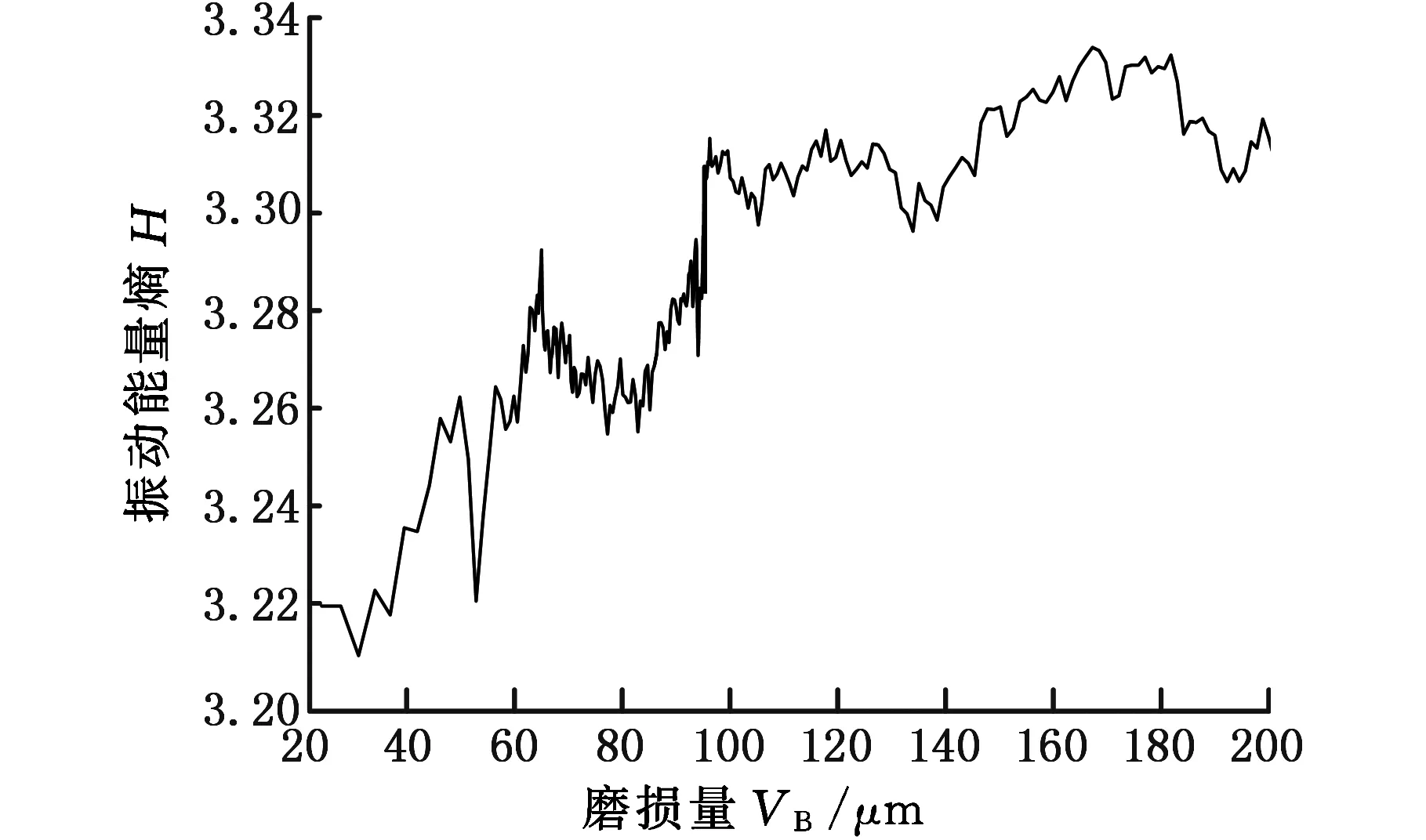
(b)小波能谱熵图7 部分频带能量和小波能谱熵变化图Fig.7 The variation curves of 4-band energy and the wavelet energy entropy

(19)

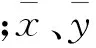
经过计算，得到时域、频域上各个特征量与磨损量间的相关系数，如表2所示。

根据表2，以|ρxy|>0.9为标准，可以筛选出一部分特征量，在X、Y、Z方向上满足条件的分别有4、2、2个特征量，故总共有8个特征量。

经过计算，X、Y、Z各个方向振动信号小波包分解后时频域上前32个频带能量和能量熵与磨损量间的部分相关系数,如表3所示。

根据表3，以|ρxy|>0.9为标准，可以筛选出一部分特征量，在X、Y、Z方向上时频域满足条件的分别有15、13、12个特征量，故总共40个特征量。

汇总时域、频域和时频域上的特征量，总共48个特征量，对这些特征量进行特征编号，如表4所示。

2.4.2灰色关联度分析

灰色信息是指外延可以确定，但是内涵不确定的、隐含而未公开的信息。两个系统中的子系统或因素间存在随时间或不同对象而变化的关联性，它们之间的相似或相异性即灰色关联度，被用作衡量它们之间的关联程度。

分析之前，首先进行数据标准化处理，即量纲一化。设参考数列X*为磨损量序列，其他数列Xi(i=1,2,…)为特征量序列，计算Xi与X*的关联系数ζi(t)。令αi(t)=|Xi(t)-X*(t)|，t表示序列中元素顺序，t∈{1,2,…,N},则有

式中，ρ∈(0,1),一般取值0.5。

表2 时域和频域特征量相关系数表Tab.2 The correlation coefficients of features in time and frequency domain

表3 时频域32个频带能量和能量熵的部分相关系数Tab.3 Parts of correlation coefficients of 32-band energy and the wavelet energy entropy in time domain

表4 特征汇总编号表Tab.4 The sequencing number of features

由关联系数得到Xi与X*的关联度

(20)

将48个编号后的特征量进行灰色关联度分析。图8为特征量关联度降序排列图。由图8可知：以关联度0.65为分界，可以淘汰掉10个特征(编号10～13，16，29，30，32，41，43)，则总共还剩余38个特征量。

图8 灰色关联度分析排序图Fig.8 Grey relational grade values and their sorting sequence

3 建模与仿真

在64位计算机MATLAB 2015b平台上编辑程序，选用高斯径向基核函数，用粒子群优化算法得到组合参数惩罚因子C=810.4、核函数参数σ2=1.2和引入参数λ=26.8。以第四组数据中的前60个数据作为训练数据，后225个数据作为测试数据，分别采用传统在线LSSVM和DNLSSVM进行225次在线预测，比较在不同滑动时间窗长度条件下，两种算法的运行时间。等间隔选取10个不同时间窗长度，对应运行时间如图9所示。

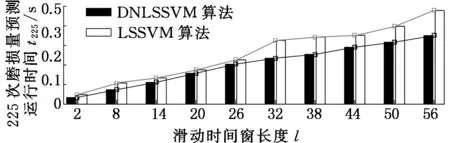
图9 算法的测试运行时间Fig.9 The test running time of DNLSSVM algorithom

由图9分析得出：随着滑动时间窗长度的增大，两种算法的测试运行时间都增长，DNLSSVM算法运行时间增长相对平稳和缓慢；一般情况下滑动时间窗长度越长，DNLSSVM的效率优势越明显。

为了平衡训练数据量和建模时间，利用滑动时间窗长度自适应调整算法，可以求取滑动时间窗长度，目标函数相对下降量随滑动时间窗长度变化如图10所示。由图10可知，在预测精度满足要求θ≤1.5 μm的条件下，选取阈值ε=0.03，可以确定滑动时间窗长度为23。

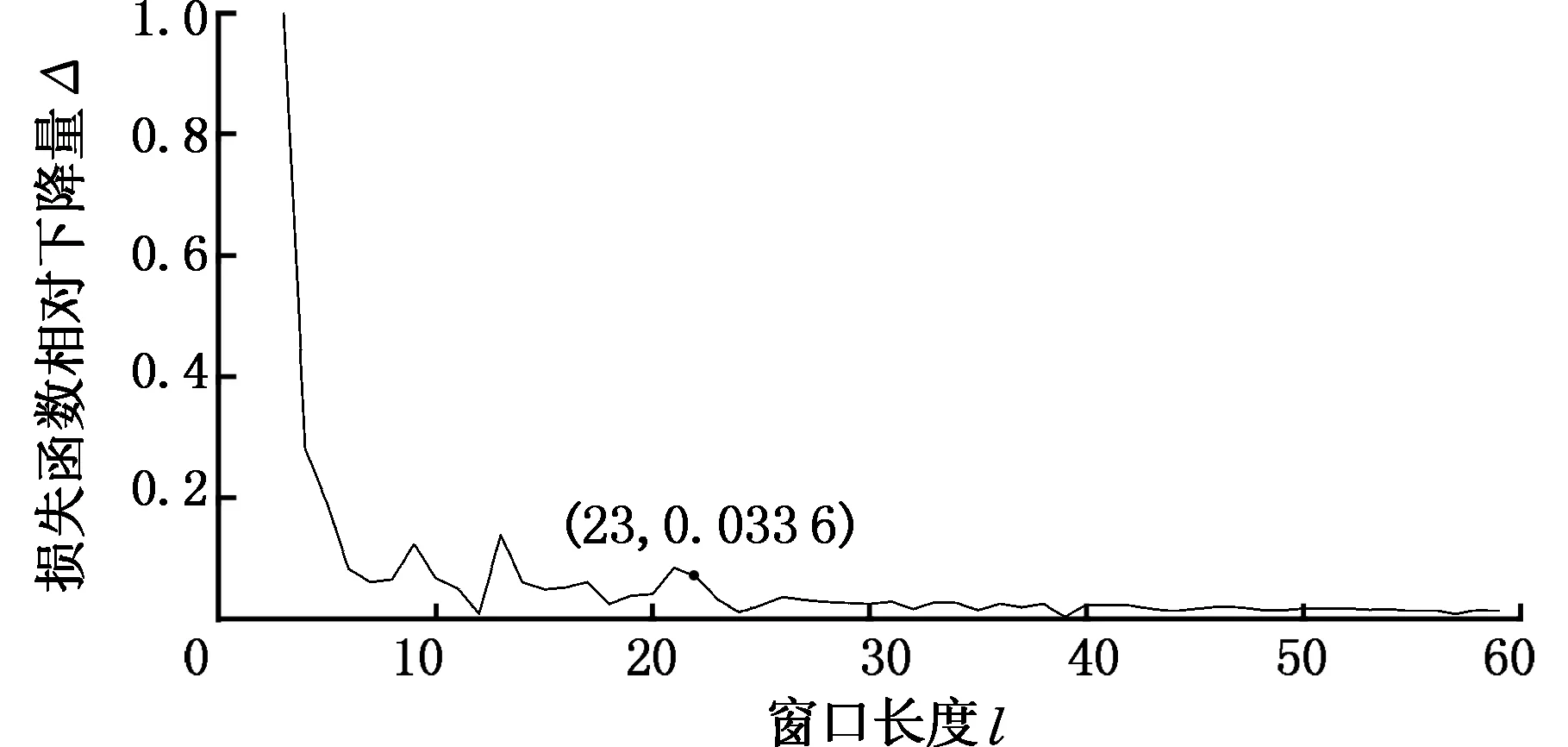
图10 目标函数相对下降量随滑动时间窗长度变化图Fig.10 The variation curve of the relative decrementof object function

输出预测仿真拟合效果,如图11所示。预测过程性能用平均相对误差r和平均绝对误差a衡量，5次试验后两种算法的预测误差见表5，计算公式如下：

由图9、图11以及表5可知，ADNLSSVM算法建模具有较好的建模效率和拟合精度。

4 结论与展望

(1)ADNLSSVM算法通过在设计上消除偏置项，增加训练样本动态增减过程，能够有效利用核扩展矩阵对称正定性质以及历史数据，提高模型的适应性，简化动态学习过程中Lagrange乘子的求解，因此该方法和传统在线LSSVM建模方法相比具有更高的建模效率，并且在滑动时间窗长度越长时优势表现越明显。

(2)自适应窗口长度确定算法兼顾了时间窗长度和拟合精度要求。与在线LSSVM算法相比，在不影响模型泛化能力的情况下，具有满足要求的拟合精度。用平均相对误差和平均绝对误差作为衡量模型精度的评价指标，试验结果表明建立的模型具有相对更好的拟合精度。

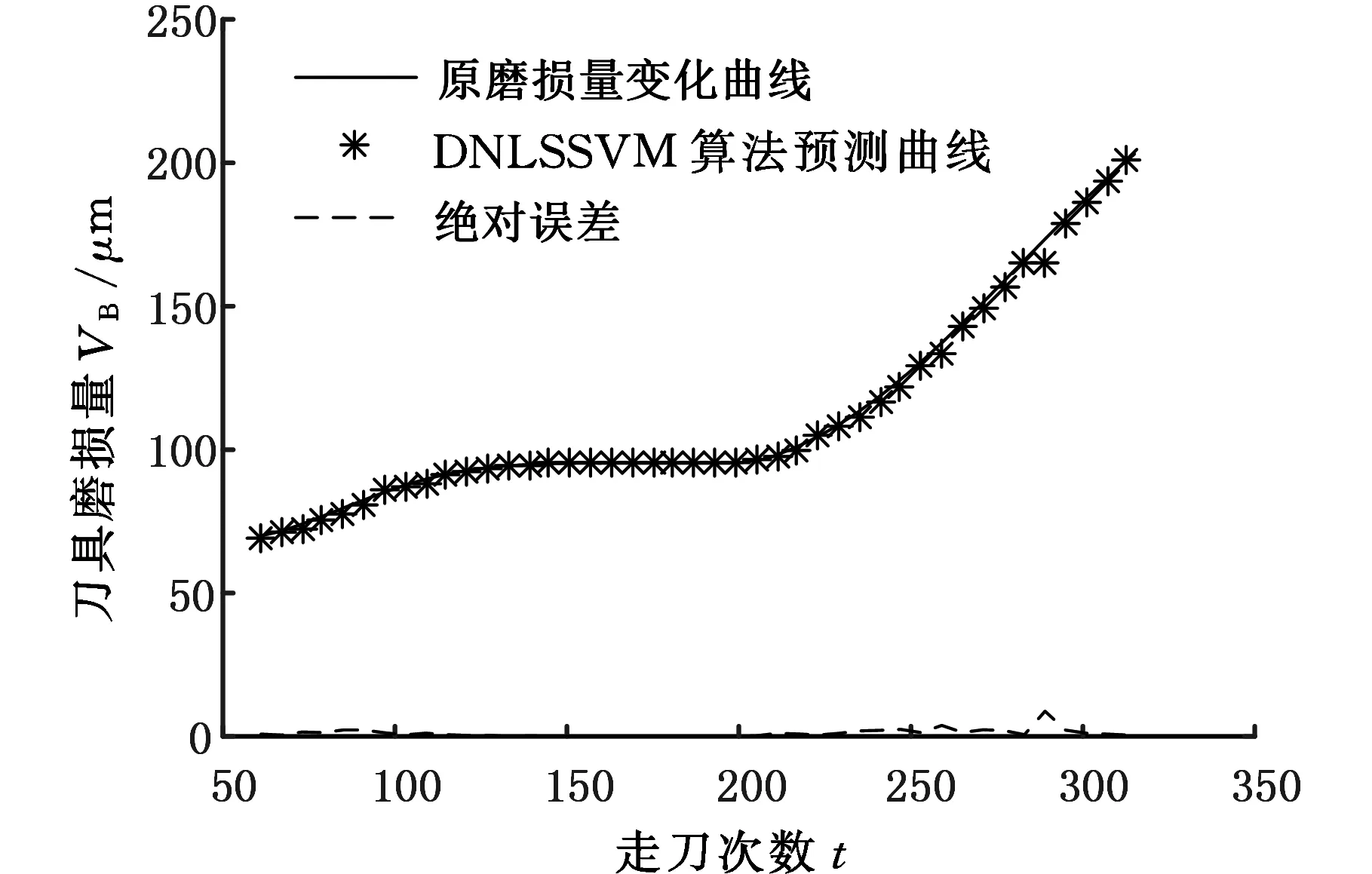
(a)DNLSSVM算法

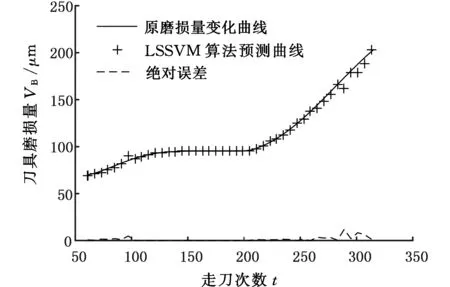
(b)LSSVM算法图11 模型拟合效果图Fig.11 Fitting performance of the prediction model

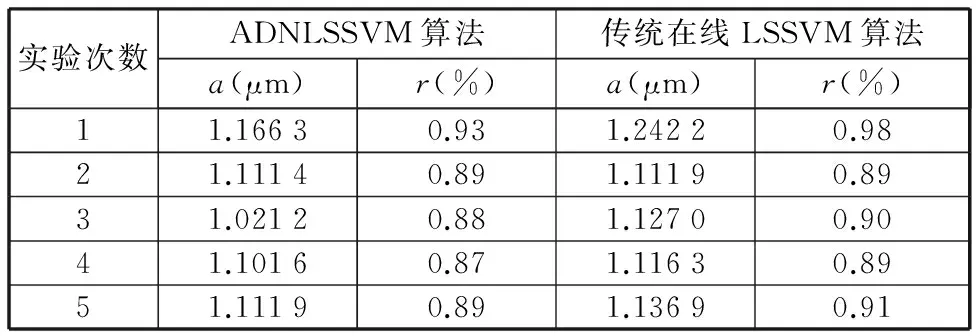
实验次数ADNLSSVM算法传统在线LSSVM算法a(μm)r(%)a(μm)r(%)11.16630.931.24220.9821.11140.891.11190.8931.02120.881.12700.9041.10160.871.11630.8951.11190.891.13690.91

(3)模型动态更新过程中需要利用上一阶段的实际磨损量，可以结合一些较为成熟的无接触直接测量刀具磨损量的技术比如机器视觉检测等技术进行状态在线跟踪和预测。

参考文献：

[1] 庄子杰.基于声发射和振动法的刀具磨损状态检测研究[D]. 上海：上海交通大学，2009.

ZHUANG Zijie. Tool Wear Condition Monition Based on AE and Vibration[D]. Shanghai：Shanghai Jiao Tong University,2009.

[2] TONSBOFF H K. Developments and Trends in Monitoring and Control of Machining Processes[J].Annual of the CIRP,1988,37(2):611-622.

[3] 杨吟飞,李亮,何宁.一种新的刀具磨损面图像边界提取方法[J].南京航空航天大学学报,2007,39(6):786-789.

YANG Yinfei, LI Liang, HE Ning. Extraction Method for Image Boundary Based on Tool Wear[J]. Journal of Nanjing University of Aeronautics and Astronautics,2007,39(6):786-789.

[4] 张臣,周来水,安鲁陵,等.球头铣刀刀具磨损建模与误差补偿[J]. 机械工程学报,2008,44(2):207-212.

ZHANG Chen, ZHOU Laishui, AN Luling, et al.Modeling and Wear-induced Error Compensation of Ball-end Milling Cutter Wear[J]. Chinese Journal of Mechanical Engineering,2008,44(2):207-212.

[5] VIJAYAKUMAR S, WU S. Sequential Support Vector Classifiers and Regression[C]// International Conference on Soft Computing. Genoa,1999:610-619.

[6] 蔡艳宁, 汪洪桥, 叶雪梅.复杂系统支持向量机建模与故障预报[M].北京：国防工业出版社,2015:4.CAI Yanning, WANG Hongqiao, YE Xuemei. Support Vecto Machine Modeling and Fault Prediction for Complex System[M]. Beijing: National Defence Industry Press,2015:4.

[7] 张浩然,汪晓东.回归最小二乘支持向量机的增量和在线式学习算法[J].计算机学报,2006,29(3):394-406.

ZHANG Haoran, WANG Xiaodong. Incremental and Online Learning Algorithm for Regression Least Squares Support Vector Machine[J]. Chinese Journal of Computers,2006,29(3):394-406.

[8] 李威霖，傅攀，张尔卿.基于粒子群优化LS-SVM车刀磨损量识别技术研究[J].计算机应用研究,2014,31(4):1094-1097.

LI Weilin, FU Pan, ZHANG Erqing. Application of Particle Swarm Optimization Least Square Support Machine in Tool Wear Monitoring[J]. Application Research of Computers,2014,31(4):1094-1097.

[9] 谢厚正,黄民.基于振动测试的数控机床刀具磨损监测方法[J].仪表技术与传感器,2013(2):73-76.

XIE Houzheng, HUANG Min. Research of Numerical Control Machine Tools Wear Monitoring Method Based on Vibration Test[J]. Instrument Technique and Sensor, 2013(2):73-76.

[10] 丛龙慧,韩玉杰.小波分析在刀具磨损状态检测中的应用[J].林业机械与土木工程,2009,37(4):51-52.

CONG Longhui, HAN Yulin. Application of Wavelet Analysis in Tool Wear Status Detection. Forestry Machinery & Woodworking Equipment, 2009, 37(4):51-52.