Maple在求解推广的Clairaut型方程中的应用

吕晓静，赵向东

（天津职业技术师范大学理学院，天津 300222）

众所周知，微分方程的学习与研究已进入计算机时代，应用数学软件中的符号计算功能可以帮助直接求解某些常微分方程，并且还可以通过计算机绘图生动形象地展示常微分方程解的几何意义。Maple语言是目前数学界较为通用的数学软件之一。在大多数的计算中，Maple不仅可以求出数值解，还可以求出解的符号式，绘出函数的二维或三维图形。

法国数学家Clairaut在1734年得到了Clairaut方程的解法。在文献[1]中将Clairaut方程作为一类一阶隐方程进行了阐述，并且引出方程奇解的定义，给出了求奇解的p-判别曲线和c-判别曲线方法。本文在此基础上，对Clairaut方程进行推广，再运用参数求解的技巧推导其通解的表达式，并且指出在推广的Clairaut方程中，不一定都有奇解，如果有的话本文也给出了奇解的表达式，更重要的是，本文针对每一种类型的方程给出了一种简便的求解方法，通过Maple程序更全面地分析了方程及方程解的性质。

1 第一类Clairaut型方程的Maple求解

在求解一阶隐方程 F（x，y，y′）=0 中，变量 x 和 y如果仅仅以复合变量xy′-y的形式出现，则有如下的结论。

命题1假设二元函数f（u，v）对2个自变量u，v二阶可导，如果一阶微分方程形如

则方程（1）的通解可表示为：

并且方程有奇解，奇解为下列方程组的解（p为参数）。

证明利用复合函数求导的链式法则，对方程（1）两端关于x求导，令y′=p

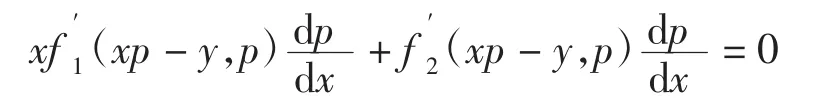
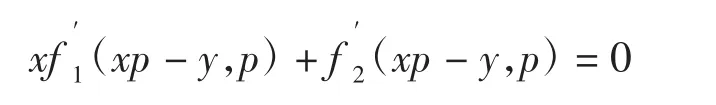
结合通解（2）得方程组（3），此时将p看做参数，通过观察可以发现，方程组（3）中的第2式恰好是第1式中对参数p的导数，因此此类推广的Clairaut方程与标准的Clairaut方程相同，方程组（3）就是原微分方程（1）的p-判别式得到的奇解。

注1：此类Clairaut型方程在文献[2]中，对照一阶隐方程的类型进行求解时，它既不属于不显含变量x或者变量y的类型，也不属于那种能够比较容易求解变量x或者变量y的类型。因此，应用Maple的程序设计进行计算很有优势，它很好地延续了Clairaut方程的求解思想，并且必有参数形式的奇解。

注 2：如果取 f（xy′-y，y′）=（x+a）y′-y+φ（y′）=（xy′-y）+ay′+ φ（y′）时，这里 a 为常数，φ（y′）是可微的，即为文献[3]中的引理 1，因此本命题的结论是对文献[3]中引理1的推广。

例 1求解方程（x2-1）（y′）2-2xyy′+y2-1=0

解将原方程化简整理为：

（xy′-y）2-（y′）2-1=0

取f（xy′-y，y′）=（xy′+y）2-（y′）2-1，则根据公式（2）和（3）编写求奇解和通解的程序如下：

解的图像源程序：

例2求解方程

解将原方程化简整理为f（xy′-y，y′）=（xy′-y）2+y′-（y′）2，则根据公式（2）和（3）编写求奇解和通解的程序如下：

解的图像源程序为：

例1和例2方程的通解和奇解的图像分别如图1和图2所示。

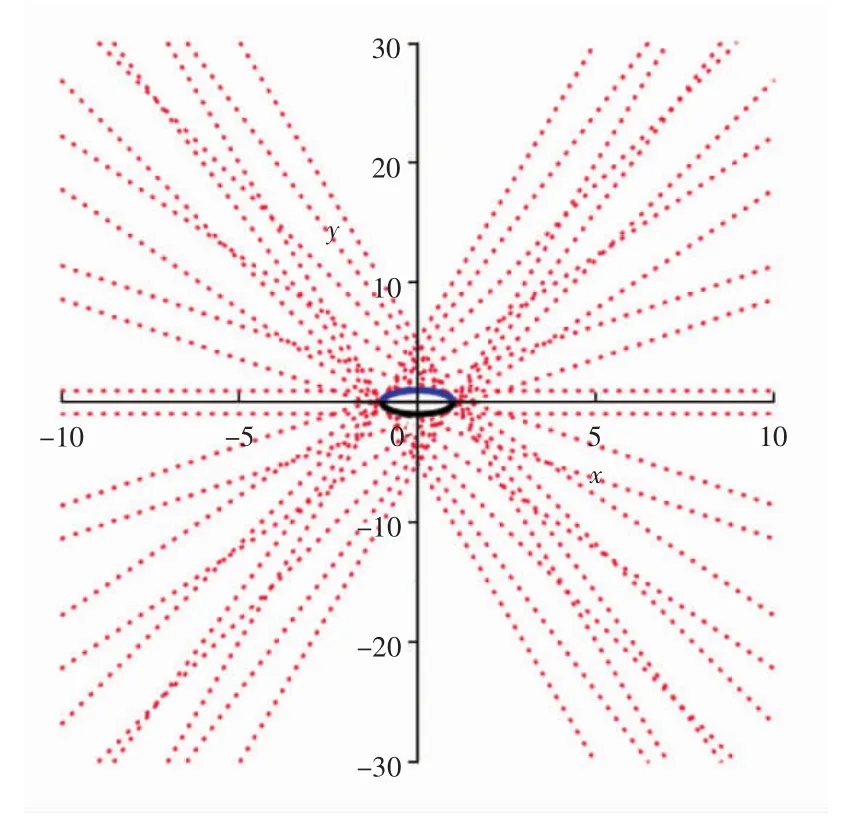
图1 例1方程的通解和奇解

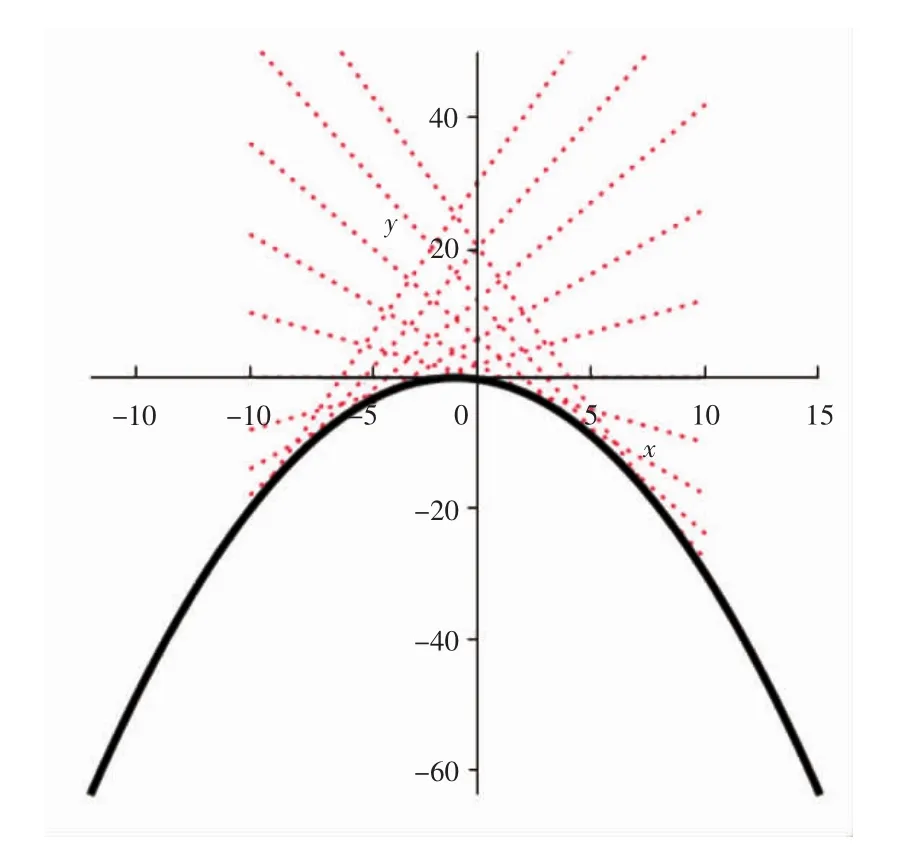
图2 例2方程的通解和奇解

2 第二类Clairaut型方程的Maple求解

命题2假设函数φ（u）对自变量u二阶可导，a为非零的常数，如果一阶微分方程形如

则关于方程的解有以下2种情况：

（1）当a≠1时，有如下的参数式通解

这里（1-a）p-ab≠0，并且

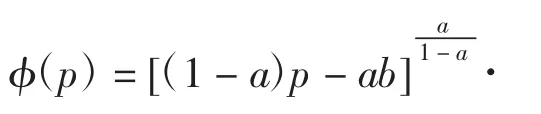
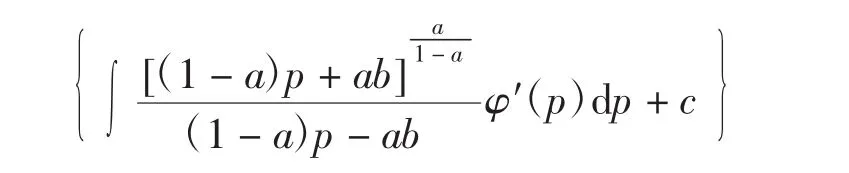
式中：c为任意常数；p为参数。特别是当（1-a）pab=0时方程有特解但非奇解，表达式为：

（2）当a=1时，有如下的参数式通解

这里 b≠0，并且

式中：C为任意常数；p为参数。特别是当b=0时方程可简化为标准的Clairaut方程。

证明利用微积分中复合函数求导的链式法则，对方程（4）两端关于 x求导，且令p=y′得

从上述表达式（8）可以看出

（1）当a≠1且（1-a）p-ab≠0得到一个关于变量x、p的一阶线性方程

因此，其通解为：

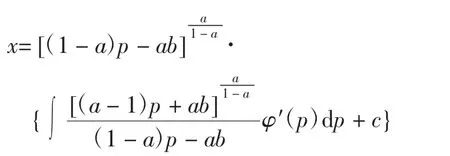
结合方程（4）得到方程组（5）；当（1-a）p-ab=0时，意味着，且等式（8）是成立的，并且易验证函数

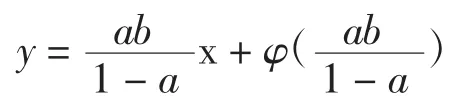
是原微分方程（4）的特解，依据文献[2]的定理3.5.1，可验证特解（6）不满足方程（4）的p-判别式。所以，此函数不是原微分方程（4）的奇解。

（2）在上述表达式（8）中，令a=1得到一个关于变量x、p的一阶线性方程

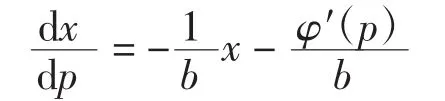
因此，其通解为：

结合方程（4）得到方程组（7）。综合以上论述，命题得证。此类Clairaut型方程无奇解。

例 3求解方程 y=2x（y′+1）+（y′）2

解根据式（5）编写求奇解和通解的程序如下：

解的图像的源程序：

当参数p∈[-10 000，0]，任意常数C取值为-10到10之间的整数时，方程通解的图像如图3所示，当参数p∈[-100 000，0]时，任意常数C取值为-10到10之间的整数时，方程通解的图像如图4所示。从图3和图4可以看出，随着p的绝对值不断减小，通解的图像在y轴左侧，从x轴上方不断地靠近x轴，y轴右侧的图像从x轴下方不断靠近x轴，最终形成直线簇。

当参数p∈[0，10 000]和任意常数C取值为-10到10之间的整数时，方程通解的图像如图5所示，当参数p∈[0，100 000]和任意常数 C取值为-10到10之间的整数时，方程通解的图像如图6所示。同理，从图5和图6也可以看出，随着p的绝对值不断减小，通解的图像在y轴左侧，从x轴下方不断地靠近x轴，y轴右侧的图像从 x轴上方不断靠近 x轴，最终形成直线簇。

综合以上情况可以看到，求解此类推广的Clairaut型方程时，借助Maple可以很好地理解为何此类方程没有奇解。

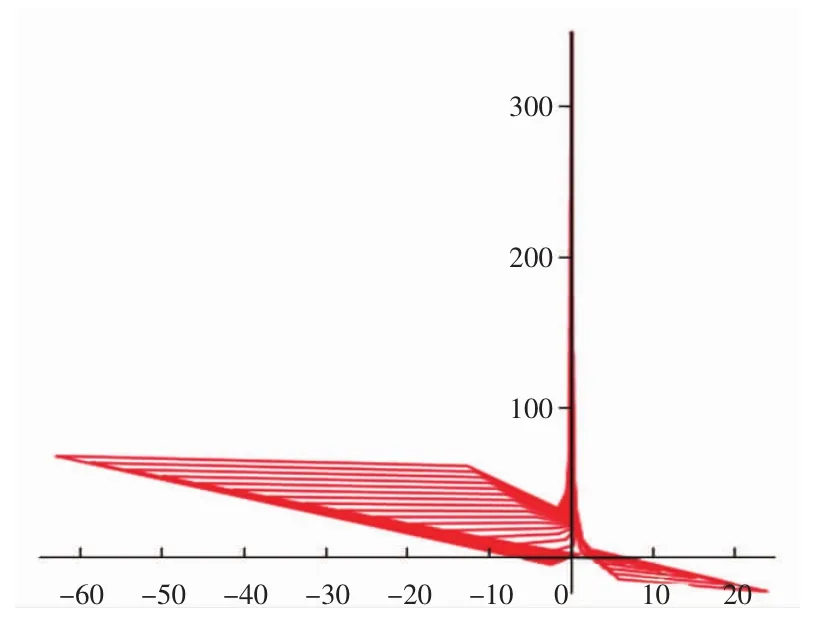
图3 例3方程的通解（参数p∈[-10 000，0]）

图4 例3方程的通解（参数p∈[-100 000，0]）

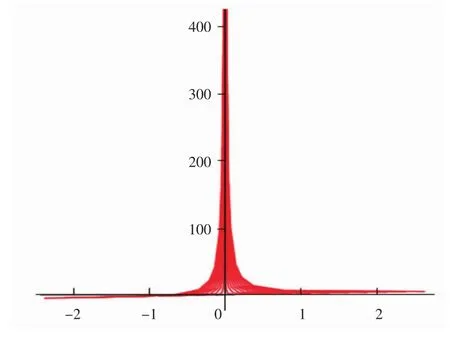
图5 例3方程的通解（参数p∈[0，10 000]）

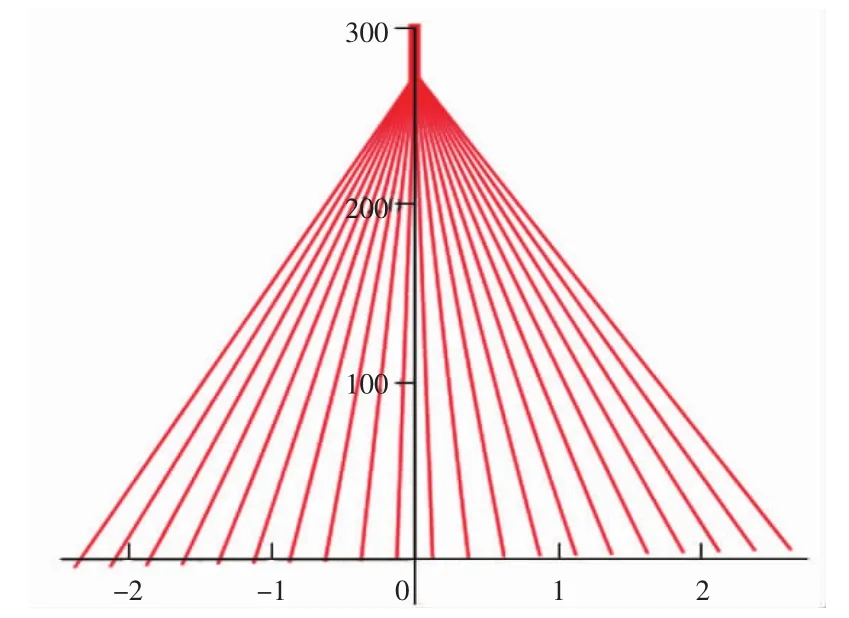
图6 例3方程的通解（参数p∈[0，100 000]）

3 第三类Clairaut型方程的Maple求解

命题3假设一元函数φ（u）对自变量u二阶可导，ab均为常数且a≠0，n为正整数且n≠0，1，如果一阶微分方程形如

则方程有参数式通解：

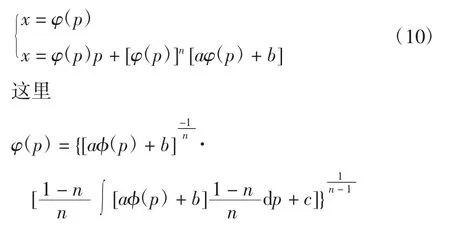
c为任意常数；p为参数。

注3：此命题的证明方法与命题2相同，不同的是最后在n＝2时求解一个关于变量x、p一阶线性方程；在n≠2时求解一个关于变量x、p的Bernoulli方程。

例 4求解方程 y=xy′+x2（2（y′）2+1）

解根据式（10）编写与例1相同的程序，求奇解和通解的曲线如下，参数p∈[-10，10]，任意常数c取值为-10到10之间的整数时，方程通解的图像如图7所示。但是，同样的题目仅仅改变n=3时，发现此时通解的图像已经完全不一样，如图8所示。可见，这一项在方程中起着至关重要的作用，而且从图形中也比较容易看出此类方程没有奇解。

图7 例4方程的通解图像（参数n=2）

图8 例4方程的通解（参数n=3）

4 结语

借助Maple软件求解以上3类推广的Clairaut型方程非常便捷，同时利用Maple软件绘出方程通解（奇解）的图像可以进一步分析得出参数形式的通解（奇解）的特性。因此，可以看出Maple软件在求解Clairaut型方程中的强大功能，这是单靠纸和笔求解方程所不能比拟的。

参考文献：

［1］王高雄.常微分方程［M］.北京：高等教育出版社，2002.

［2］王鸿业.常微分方程及Maple应用［M］.北京：科学出版社，2011.

［3］昌山.CLAIRAUT型方程的推广与求解［J］.江汉大学学报，1993，10（2）：23-28.

［4］Staff of Research Education Association.Problem Solvers Differential Equations［M］.Piscataway：REA，2008.

［5］LYU X J，QIAN T，SCHULZE B W.Order filtrations of the edge algebra［J］.Pseudo-Differential Operator Applying，2015，6（3）：279-305.

［6］LYU X J，SCHULZE B W.Mellin Operators in the edge calculus［J］.Complex Analysis and Operator Theory，2016，10（5）：965-1000.

［7］LYU X J.Asymptotics in weighted corner spaces［J］.Asian-European Journal of Mathematics，2014，7（3）：1450050-1450086.

［8］CHANG D C，LYU X J，SCHULZE B W.Recent developments on pseudo-differential operators（II）［J］.Tamkang Journal of Mathematics，2015，46（3）：281-347.