自关联算法在光学相关识别中的应用

徐德芹，盛朝霞，马 婧

（天津职业技术师范大学理学院，天津 300222）

光学相关图像识别是一种利用光学实现相关的方法，将所需要的目标图像识别出来的新技术。光学相关图像识别的优点是高速、便捷、可并行处理，在军事、医学、信息安全等很多领域被广泛应用。联合变换相关是光学相关识别中一种主要的识别方法。联合变换相关器（joint transform correlator，JTC）的基本构架是4f光学系统[1]，将待识别图像和参考图像利用透镜实现2次傅里叶变换得到图像的相关输出，从而实现图像的识别。人们已经采取了各种研究方法对多目标识别和在有背景噪声的情况下的相关识别[2-8]。关联成像，是近几年量子光学领域的研究热点之一。许多研究学者对此进行了很多理论和实验研究[9-20]。其中，量子亚波长和热光亚波长实验进一步证明利用关联成像可以实现无透镜的傅里叶变换，提高了刻录的精度。为了克服经典瑞利衍射极限的约束，许多研究者将量子亚波长效应应用在提高成像分辨率上，得到亚瑞利分辨成像[21-26]。本文论述了光学相关图像识别中联合变换相关器的基本理论，结合关联成像中的自关联算法可以在空间域实现无透镜傅里叶变换，改善和提高光学图像识别的抗干扰性、准确性和并行性。新型的联合变换相关器简化了实验装置，提高了识别率和抗干扰性，使其更加便携。

1 联合变换相关器的基本原理

联合变换相关器和自关联光学相关识别如图1所示。

图1（a）中，在输入面P1上放置待识的目标图像f（x，y）和参考图像 h（x，y），待识别图像 f（x+b，y）中心位于（-b，0），参考图像 h（x-b，y）中心位于（b，0）。用准直光照射图像f（x，y）和h（x，y），经过透镜的傅里叶变换后，在频谱面上的复振幅分布为：

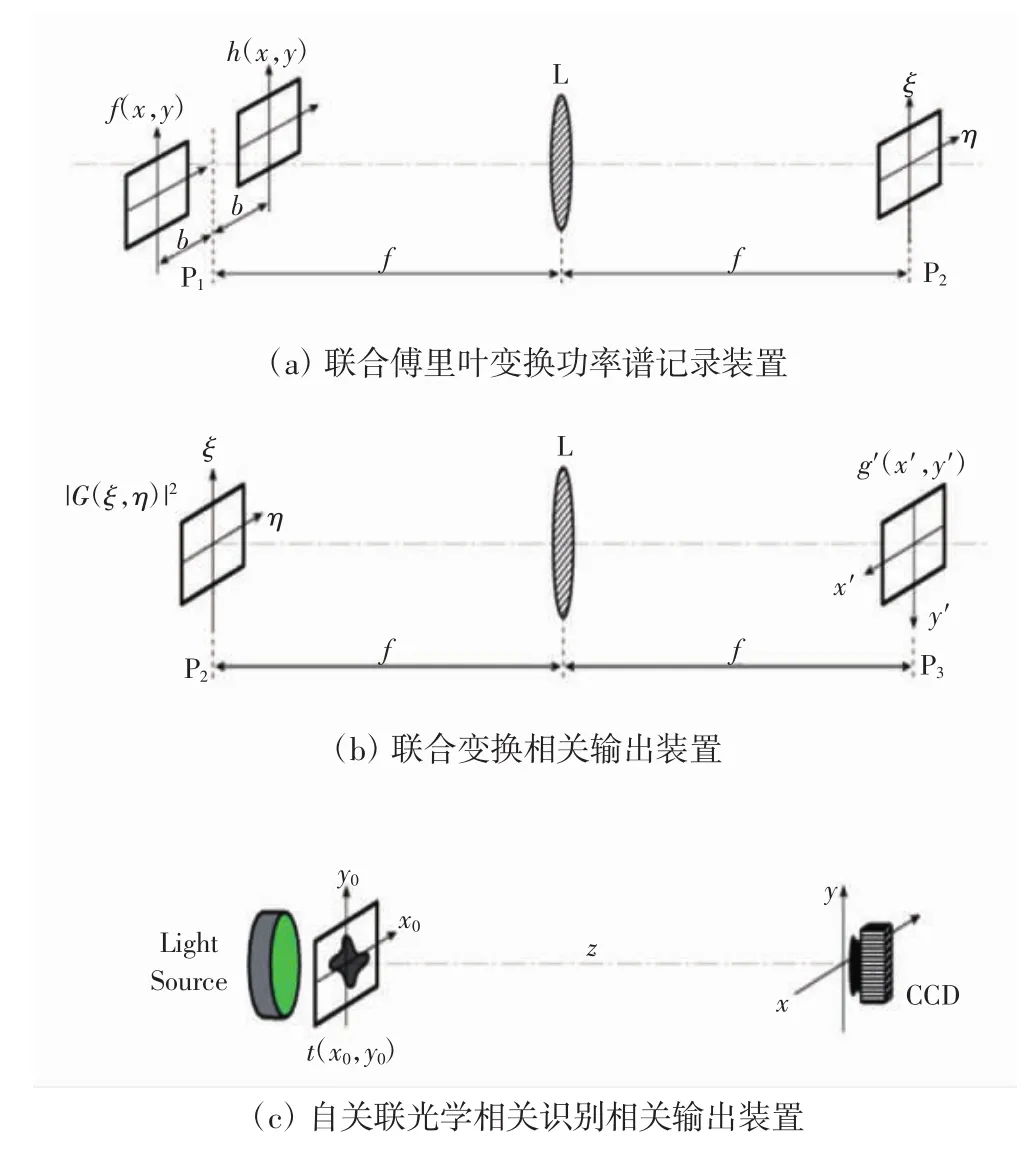
图1 联合变换相关器和自关联光学相关识别

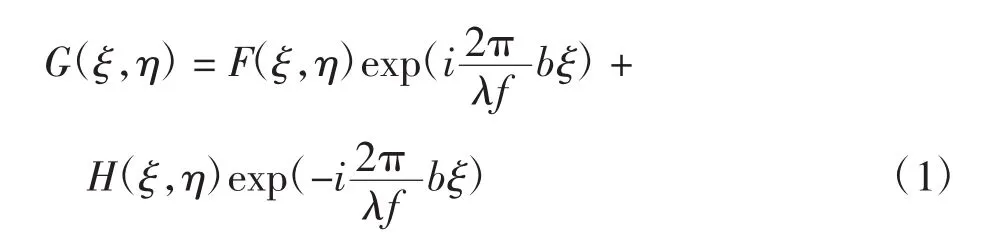
式中：f是透镜 L 的焦距；F（ξ，η）和 H（ξ，η）分别为待识别图像 f（x，y）和参考图像 h（x，y）的傅里叶变换。

观察屏P2上的功率谱是光强度的分布，采用器件CCD记录，则功率谱的表达式为：

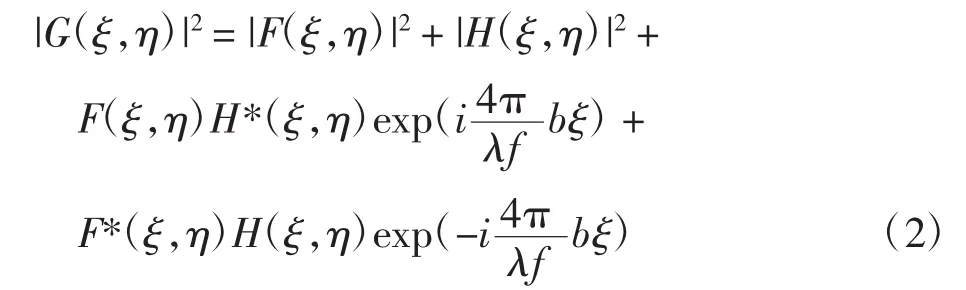
功率谱的强度分布经液晶光阀转换，在线性记录条件下，如图1（b）所示。用单位振幅的相干光读出，经透镜L的逆傅里叶变换后在输出面的相关输出为：

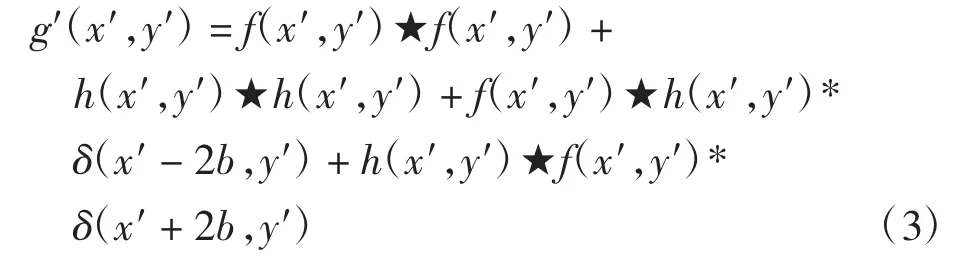
式中：★为相关运算符号；*为卷积运算符号。式（3）中的第一、二项分别表示待识别图像和参考图像的自相关，它们重叠位于输出面中心，构成零级衍射，不是本研究需要的信号；而2个共轭的互相关项分别为第三项，位于（2b，0）处和第四项，位于（-2b，0）处，与中心零级衍射分离，称为一级项。如果在（±2b，0）附近产生相关的亮斑（即出现相关峰），那么待识别图像f（x，y）和参考图像 h（x，y）相关程度较大，否则，在（±2b，0）附近出现暗的弥散斑（即没有相关峰），两者的相关度较小。

2 自关联算法的光学相关识别

将图1（b）的装置用图1（c）装置替换，用自关联算法实现无透镜的傅里叶变换，实现功率谱的逆傅里叶变换过程，得到图像识别的相关输出。图1（c）中，赝热光源照射物体，经过自由传播到达探测器，将探测器测得强度做自关联处理。

在关联成像中的强度关联为：

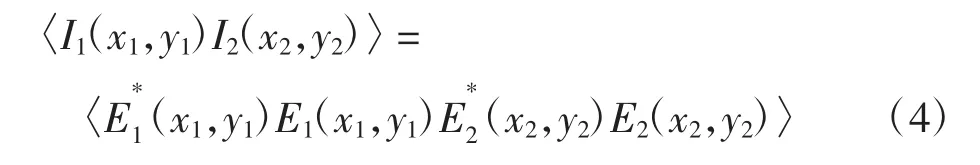
式中：Ii为探测器的强度分布；Ei为探测器的光场分布。

强度涨落的关联为：

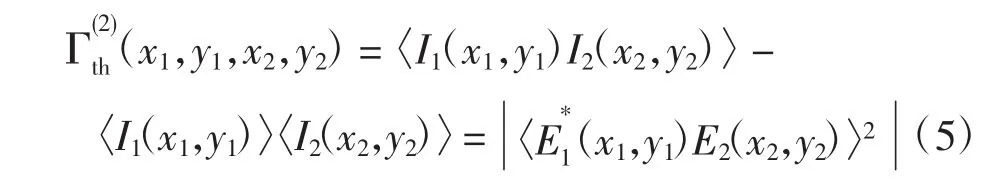
热光的自关联算法中

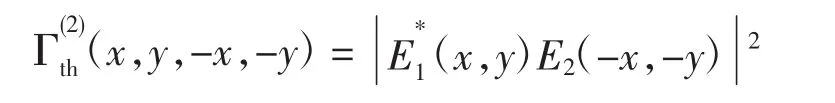
赝热光源照射物体自由传播过程的脉冲响应函数为：

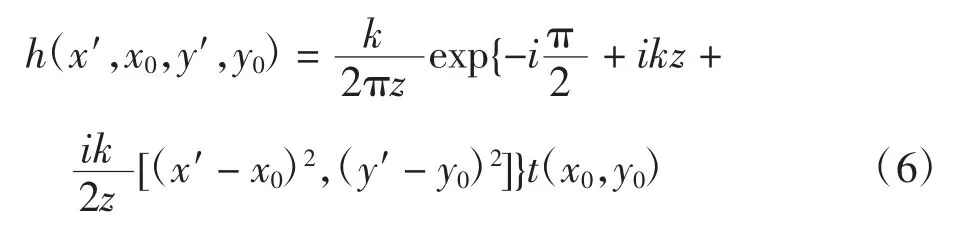
式中：（x0，y0）为光源面上的横向坐标；（x′，y′）为探测器面上的坐标；z为物体到探测器CCD的距离。

一阶光场的互相干函数为：

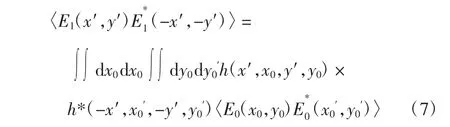
假设空间非相干光源为无限大且完全非相干，则

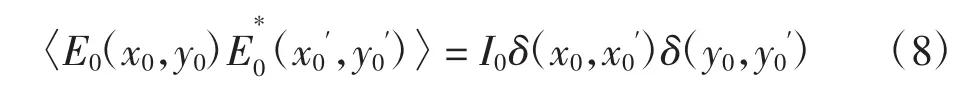
式中：E0为光源处的光场分布；I0为光源处光的平均强度。则

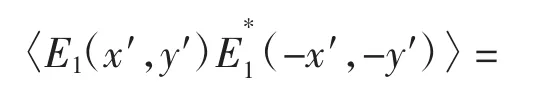
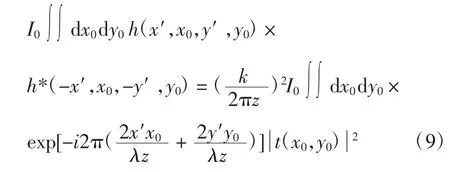
若作为物体的透过率函数，则

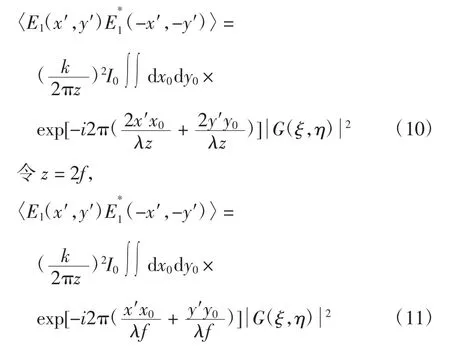
将式（2）代入式（11），对功率谱做逆傅里叶变换，与透镜的逆傅里叶变换作用一样，因此在满足线性记录条件下，可以得到与式（3）完全相同的结果，实现图像识别的相关输出。

由此得出，在联合傅里叶变换相关器中，需要用相干光源照射记录介质通过透镜做逆傅里叶变换实现相关输出。而在自关联算法中，使用赝热光源（即非相干光源）照射记录介质自由传播距离z，且z=2f即可实现逆傅里叶变换，达到相关输出。

3 结语

本文从理论上分析了自关联算法在光学相关识别的相关输出，得到与联合傅里叶变换相关器相同的结果。但是在自关联算法中，利用非相干光源实现无透镜的傅里叶变换，突破了联合傅里叶相关器相干光源的限制，同时简化了光路，光路的稳定性得到改善，提高了抗干扰能力，使得光学相关图像识别器便携化，实用化，扩大了其应用范围。

参考文献：

［1］吕乃光.傅里叶光学［M］.北京：北京大学出版社，1998.

［2］JAVIDI B，WANG J.Binary nonlinear joint transform correlation with median and Sub-Set median thresholding［J］.Applied Optics，1991，30（8）：967-976.

［3］JAVIDI B，ODEH S F.Multiple object identification by bipolar joint transform correlation［J］.Optical Engineering，1988，27（4）：295-300.

［4］FIELDING S F，HORNER J L.1-f Binary joint transform correlator［J］.Optical Engineering，1990，29（8）：1081-1087.

［5］LI C T，YIN S Z，FRANCIS T S Y.Nonzero-order joint transform correlator［J］.Optical Engineering，1998，37（1）：58-65.

［6］WANG H X，ZHAO W，LI Y X.Multi-object recognition using power spectrum optimized joint transform correlator［J］.Optical Technique，2006，32（2）：190-195（in Chinese）.

［7］SHEN X J，ZHOU S G，WANG L.Characteristics of joint transform correlators under the illumination of Gaussian beam［J］.Laser Technology，2009，33（4）：429-432（in Chinese）.

［8］SHENG Z X，SUN X L.Application of computer generated hologram technology in optical correlation recognition system［J］.Laser Technology，2008，32（1）：61-63（in Chinese）.

［9］PITTMAN T B，SHIH Y H，STREKALOV D V，et al.Optical imaging by means of two-photon quantum entanglement［J］.Physical Review A，1995，52（5）：3429.

［10］BENNINK R S，BENTLEYS J，BOYD R W.“Two-photon”coincidence imaging with a classical source［J］.Physical Review Letters，2002，89（11）：113601.

［11］CHENG J，HAN S S.Incoherent coincidence imaging and its applicability in X-ray diffraction［J］.Physical Review Letters，2004，92（9）：93903.

［12］GATTI A，BRAMBILLA E，BACHE M，et al.Ghost imaging with thermal light：comparing entanglement and classical correlation［J］.Physical Review Letters，2004，93（9）：93602.

［13］XIONG J，CAO D Z，HUANG F，et al.Experimental observation of classical subwave length interference with a pseudothermal light source［J］.Physical Review Letters，2005，94（17）：173601.

［14］CAO D Z，XIONG J，WANG K.Geometrical optics in correlated imaging systems［J］.Physical Review A，2005，71（1）：13801.

［15］LI H，CHEN Z，XIONG J，et al.Periodic diffraction correlation imaging without a beam-splitter［J］.Optics Express，2012，20（3）：2956-2966.

［16］VALENCIA A，SCARCELLI G D，ANGELO M，et al.Twophoton imaging with thermal light［J］.Physical Review Letters，2005，94（6）：63601.

［17］MEYERS R，DEACON K S，SHIH Y H.Ghost-imaging experiment by measuring reflected photons［J］.Physical Review A，2008，77（4）：41801.

［18］ZHANG D，ZHAI Y H，WU L A，et al.Correlated twophoton imaging with true thermal light［J］.Optics Letters，2005，30：2354.

［19］CAI Y，ZH1U S Y.Ghost imaging with incoherent and partially coherent light radiation［J］.Physical Review E，2005，71（5）：56607.

［20］LI H，ZHANG Y，SHI J，et al.Experimental realization of reflection-type periodic diffraction correlation imaging［J］.Applied Physics Letters，2013，102（20）：201901.

［21］ANGELO M D，CHEKHOVA M V，SHIH Y H.Two-photon diffraction and quantum lithography［J］.Physical Review Letters，2001，87：13602.

［22］JACOBSON J，BJORK G，CHUANG I，et al.Photonic de broglie waves［J］.Physical Review Letters，1995，74：4835.

［23］THIEL C，BASTIN T，ZANTHIER J V，et al.Sub-rayleigh quantum imaging using single-photon sources［J］.Physical Review A，2009，80：13820.

［24］GIOVANNETTI V，LLOYD S，MACCONE L，et al.Subrayleigh-diffraction-bound quantum imaging［J］.Physical Review A，2009，79：13827.

［25］GUERRIERI F，MACCONE L，WONG F N C，et al.Subrayleigh Imaging via N-photon detection［J］.Physical Review Letters，2010，105：163602.

［26］OH J E，CHO Y W，SCARCELLI G，et al.Sub-rayleigh imaging via speckle illumination［J］.Optics Letters，2013，38（5）：682.