广义统计的参数及其相互关系

郭丽娜

（天津职业技术师范大学理学院，天津 300222）

著名物理学家玻尔兹曼在19世纪提出了经典的玻尔兹曼统计规律，历经众多实验验证，已在很多领域得到了应用。但是，近些年的研究发现，有些情况下，如存在长程相互作用的非平衡系统，玻尔兹曼统计表现出极大的局限性，因而人们开始对经典的玻尔兹曼熵进行推广，其中最具代表性的就是Tsallis熵。这一全新形式的熵不再像玻尔兹曼熵那样具有广延性，而是一种非广延性的熵。这使得Tsallis统计具有了很多玻尔兹曼统计所不具备的性质，并因此而应用到很多不同的领域。除此之外，通过引入参数，以不同的形式推广玻尔兹曼熵后可以得到不同的广义熵，进而得到很多不同种类的广义统计。本文研究了Tsallis非广延性熵、κ熵、Abe熵以及更为广泛的双参数广义熵函数的参数同系统的温度梯度和外场力之间的关系式，分析了各种统计中参数的物理意义，并由此得到不同的广义统计之间的关系和各自适用范围，为进一步寻找广义统计的应用领域提供帮助。

1 经典玻尔兹曼统计

1.1 玻尔兹曼统计

19世纪发展起来的统计物理学将物体的宏观性质和微观状态联系起来，从微观的角度解释了物体的宏观性质。由于从宏观角度无法区分每一个微观粒子，所以对于某一物理系统而言，同一个宏观状态其实对应了许多个不同的微观状态。对于孤立系统来说，不管系统的初始状态如何，经过一段时间后，系统总是趋向于几率分布不再发生变化的状态，也就是宏观平衡态。而统计物理学中的一个根本问题正是孤立系统处于平衡态时各个微观状态出现的几率是多少。玻尔兹曼作为统计物理学中里程碑式的科学家，提出了等几率假设：系统中所有可能的微观状态出现的几率都是相同的，或者说任何一个微观状态都是彼此平权的。因此，对于理想气体系统而言，如果处于宏观状态下的统计平衡态，那么理想气体分子间的碰撞相互作用、气体分子与容器壁的碰撞相互作用等都是随机的。因此，没有理由认为某一个微观状态出现的几率比其他的微观状态更大。从这一假设出发，它的各种推论都和实验相符合，因而它也成为了统计物理学中的一个基本假设，被广为接受。

麦克斯韦-玻尔兹曼分布律就是从这一假设出发，描述密闭容器中孤立系统的理想气体分子处于平衡态时，按能量分布的分布函数，即

式中：C为归一化系数。玻尔兹曼分布是热力学几率的最大的宏观分布。

1.2 玻尔兹曼统计力学具有局限性

自19世纪玻尔兹曼统计物理学问世以来，由于其所描述的系统宏观特征和实验能够很好地符合，因而获得广泛应用，成为最重要的统计工具。但是，麦克斯韦-玻尔兹曼统计所描述的是处于平衡态下的理想气体模型，也就是说，对于某些非平衡系统[1～3]，如长程相互作用系统[4]，它是不适用的。

恩里克·费米在《热力学》一书中指出[5]：一个由几部分组成的系统的熵正好等于其的各个部分的熵之和。当系统的能量为其他各部分能量之和，或者是一个系统在其变换过程中做的功等于其各个部分做的功总和时，这种表述是正确的。例如，某一系统是由系统A和系统B所组成的，那么该系统的熵就等于原来系统A 和系统B的熵之和，即S（A+B）=S（A）+S（B）。但是，特别要注意的是它所说的前提条件并不是对于所有的系统都一定满足。也就是说，对于存在着长程相互作用的系统，各个分系统的能量相加并不等于组合系统的能量。这时，总系统的熵就不再是分立系统A和系统 B 的熵之和，即 S（A+B）≠S（A）+S（B）。假如还是利用麦克斯韦-玻尔兹曼统计进行描述，就会有所局限[6]。对于玻尔兹曼统计力学所遇到的困难，英国物理学家兰兹伯格在1978年提出[7]：为了描述长程力，有必要对热力学进行修正，其中的一些问题还需要进一步的研究。

正是经典的麦克斯韦-玻尔兹曼统计力学具有的局限性[8]，说明某些具有长程相互作用的物理系统超出了它的适用范围。所以，必须对这一经典理论进行推广，从而能够描述更多更复杂的物理系统。同时，推广后的理论通过取得某些特定值，还应该能够回到原来的玻尔兹曼理论，从而使得新理论具有更为普遍的应用范围。

1.3 熵

为在物理上实现对经典玻尔兹曼统计力学的推广，就需要在传统统计中寻找一个出发点，而传统热力学中最为重要的核心概念就应当是熵。将熵作为这个出发点，那便是最大熵原理。

作为信息论的创始人，香农于20世纪从信息论的角度提出香农熵：

式中：pi为物理系统第i个微观态的概率，满足

W为系统微观状态的总数。所以一个物理系统的内能可以定义为：

式中：Ei为系统的第i个微观态的能量本征值。在等几率原理假设下，pi=1/W，此时香农熵就可以回到平衡态下的玻尔兹曼熵：

因此，熵的概念更加丰富，无论是在平衡态时，还是非平衡态时，甚至是不可逆过程中，熵都有了物理意义。后来，杰尼斯提出：最大熵原理不具任何物理意义，而仅仅是一个推论的工具。可以利用对熵取极值的方法，并在条件（2）和（3）的限制下，人们能够从熵的角度，分别在系综论和分子运动论中重新推导出整个传统统计力学。

既然最大熵原理并不局限于某一类物理系统，而是普适的，那么就可以将它直接作为新统计理论的基本原理。通过推广熵函数的数学形式，建立新的广义统计理论。玻尔兹曼熵，可写为：

显然，式中的对数函数满足可加性

这就使得玻尔兹曼熵也具有了这种可加性

即由系统A和系统B所组成的新系统的熵等于原来系统A和系统B的熵之和，所以在玻尔兹曼统计理论中，熵是广延量。正如之前所说，人们可以从推广玻尔兹曼熵的形式出发得到新的统计理论，但是对于推广后新的熵，则可能就不再满足该可加性了。

2 非广延性q熵及其参数

对经典广延性的熵推广时，可以把方程（5）推广为：

这正是1988年由巴西物理学家Tsallis[9]提出的推广后的熵。其中，定义广义对数函数此时，对于A和B两个相互独立的系统，它们的微观态概率和经典统计一样，都可以满足

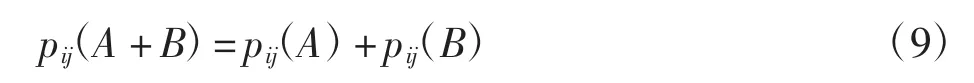
但不同的是，此时它们总系统的熵却不满足可加性，即Sq（A+B）≠Sq（A）+Sq（B），而只满足一种伪可加性

显然，在q≠1时，Tsallis熵不是广延的。而取极限q→1时，Tsallis熵函数回到了经典的玻尔兹曼熵，重新成为广延量。所以，引入的参数q就是物理系统非广延性的量度，其取值同1偏离的程度表示了系统的非广延性程度。

获得了推广后的非广延熵，就可以对广义对数函数取反函数，得到广义的e指数函数，exp（x）=[1+，从而得到Tsallis分布函数

式中：C为归一化系数。

自从Tsallis非广延性统计力学提出后，众多不同领域的研究都取得了新的进展。在自引力系统、非线性动力学系统[10]、金斯判据[11]、铁磁系统[12]、一维Ising模型[13]、纯电子等离子体系统[14]、量子气系统[15]、Lévy奇异分布[16]及核反应[17]等方面成功解释了某些经典统计无法解释的现象，从而获得了广泛的认同。

然而，这些大量的关于Tsallis非广延统计应用的研究，却更加需要对其参数q的物理意义的深入理解，从而能够更好地分析非广延性统计和玻尔兹曼统计之间的关系。因此，通过广义的玻尔兹曼方程，研究具有一定温度梯度的非平衡定态系统，可以得到参数q的关系[18～19]与系统的温度梯度和外场力F=e▽φ之间的数值关系

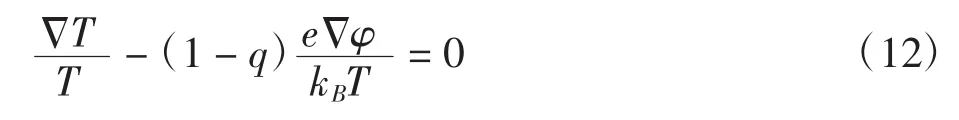
从方程（12）中可以发现参数q同1之间的差异表示了系统温度梯度的大小，也就是系统偏离平衡态的程度，这也印证了之前所说的参数q可以反映系统的非广延性的大小。另一方面，方程（2）～（5）也说明了在非广延q统计下，要求系统的温度梯度的方向和系统所受到的外场力F=e▽φ的方向平行。这也就是说，非广延性q统计更适用于描述温度梯度方向和外场力方向相平行的系统，例如自引力天体系统[20]。

3 κ熵及其参数

除了Tsallis非广延性q统计，还有多种不同的广义统计，通过不同的方式推广玻尔兹曼熵，引入不同的参数，对经典的玻尔兹曼统计进行推广，从而描述不同的非平衡态系统。其中最为常见的是由Kaniadakis提出的κ统计[21～22]，其熵函数可以写为：

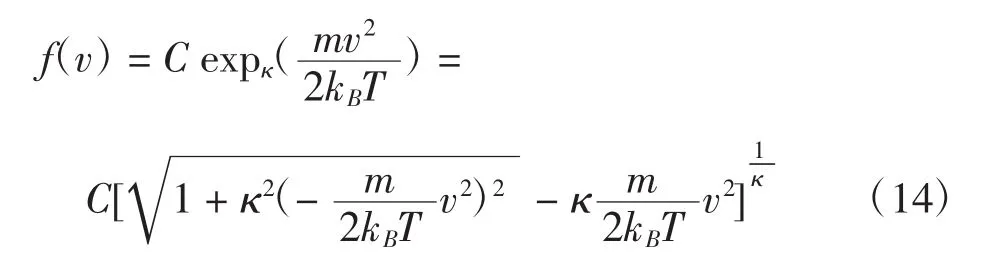
式中：C为归一化系数。当参数κ=0时，方程（13）中的κ熵函数回到经典的玻尔兹曼熵，方程（14）中的κ分布函数回到玻尔兹曼分布。

同样利用广义的玻尔兹曼方程，考虑一个由N个粒子组成的系统，处在外力场F的作用下。对于该非平衡定态系统，可以在κ统计下分析其参数κ同温度梯度和外场力F之间的关系为[23]：

这意味着参数κ同样能表示非平衡系统温度梯度的大小，κ同0的偏离值表明了该系统偏离平衡态的程度，即κ统计偏离玻尔兹曼统计的大小。然而，与非广延q统计不同的是方程（15）说明了在κ统计下，系统所受到的外场力F的方向和温度梯度是彼此垂直的。因此，κ统计更适合于描述外场力F的方向和温度梯度垂直的非平衡系统。

非广延q统计和κ统计虽然都可以描述非平衡定态系统，但它们所适用的系统却不同。这表明不同的非平衡系统可能需要不同的广义统计来描述，因此有必要研究不同广义统计参数的物理意义，由此推断它们各自所适用的系统。

4 双参数广义统计

为了理清不同种类的广义统计之间的关系，Kaniadakis[24]提出了一种双参数的广义统计，其熵函数中的广义对数函数可写为：

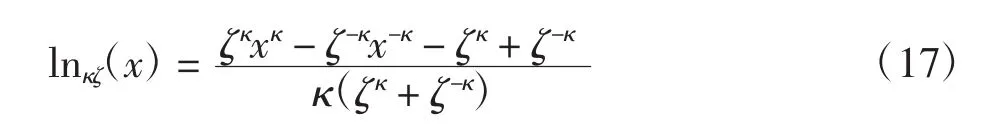
从方程（17）中可以发现，在取极限ζ→0时，可以得到广义的q对数函数；或者也可以令ζ=1，从而得到κ统计中的广义对数函数lnκ（x）=也就是说，从这种双参数广义统计出发，可得到Tsallis统计、κ统计，或者更多的不同形式的广义统计。

另外，利用广义的玻尔兹曼方程，分析这种双参数广义统计中的2个参数κ、ζ，就可得到[25]

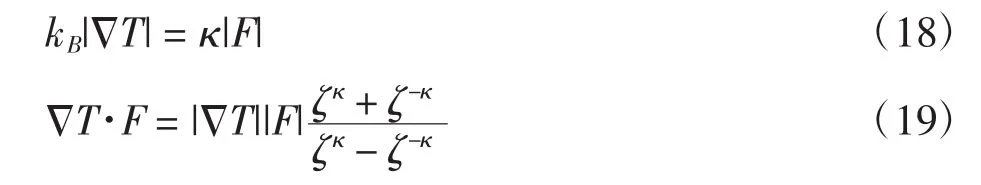
从方程（18）中，可以看到双参数中的参数κ表示了系统的温度梯度的大小，也就是表示了系统偏离平衡态的程度，即该广义统计偏离经典玻尔兹曼统计的程度。方程（19）表示了温度梯度和外场力F之间夹角的余弦值。也就是说，双参数广义统计可以描述具有一定温度梯度的非平衡定态系统，并且系统温度梯度的方向和其所受到的外场力的方向之间夹角的余弦值可以用表示。

作为这种双参数广义统计的2个特例，Tsallis非广延q统计和κ统计同样可以描述非平衡定态系统，各自的特征参数可以作为它们偏离经典玻尔兹曼统计的量度。然而，不同形式的广义统计，其可以是不同的，这就使得它们能够描述的系统的温度梯度和外场力F之间的夹角可以不同，即不同形式的广义统计所适用的系统可能不同。这对于寻找广义统计所适用的应用领域具有非常重要的指导意义。

5 Abe广义熵函数

从双参数广义统计可知，当其参数κ、ζ取不同值时，可得到不同的广义统计，经过一系列代数运算[26]得到Abe在1997年提出的另一种广义熵[27]

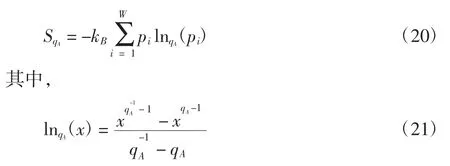
式中：当参数qA→1时，广义对数函数式（21）回到标准自然对数函数形式。由此，可以将分布函数写为：

为了分析参数qA在熵函数中的物理意义，首先研究一个由N个粒子所组成的广义动力学系统。假设该系统中每个粒子的质量为m，则其分布函数表示粒子处在相空间（x，v，t）处的几率。如果系统处于外场力F的作用下，那么它就满足描述系统动力学规律的广义玻尔兹曼方程

式中：C（fqA）为碰撞项。当系统处于广义平衡态时，方程（23）中的碰撞项为零，即满足：

方程（25）两边同时对坐标求梯度，可得到：

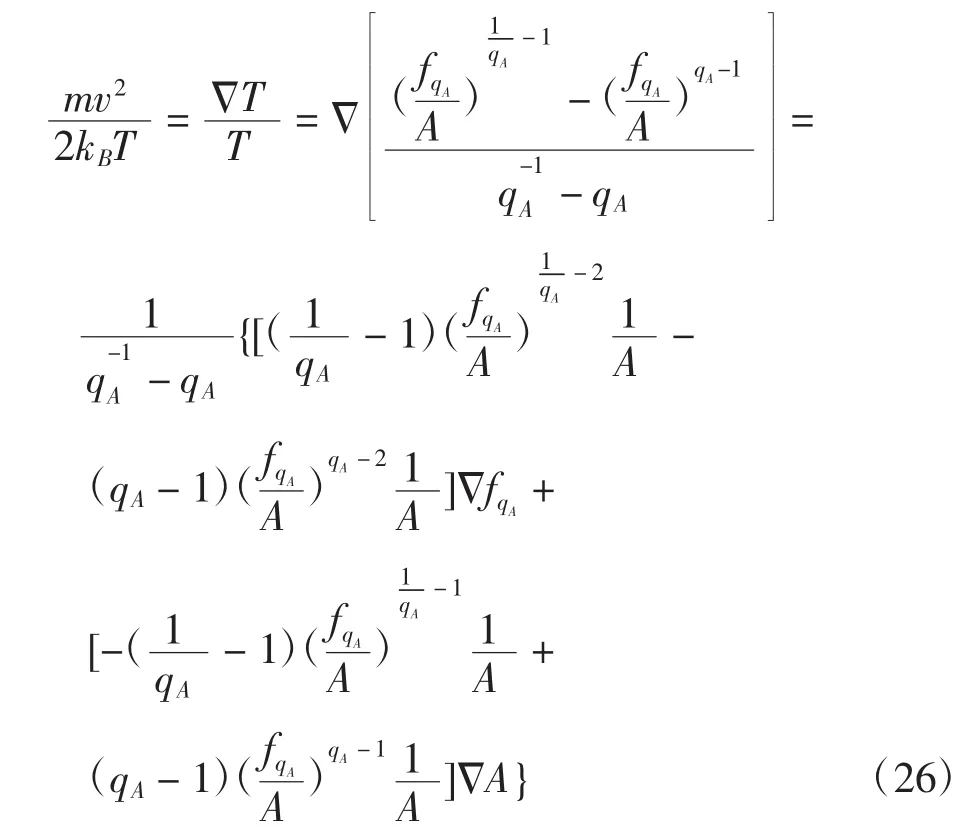
方程（25）两边同时对速度求梯度，可得到：

由方程（26）可得到：

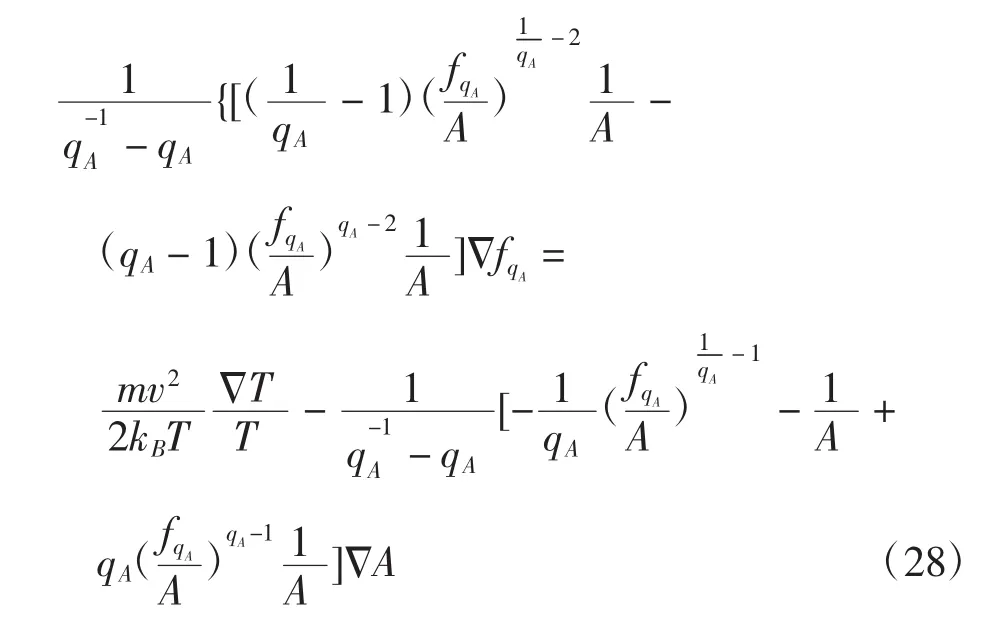
将方程（27）和（28）代入到方程（24），可得到：

经整理化简后，利用方程（25），可得到：

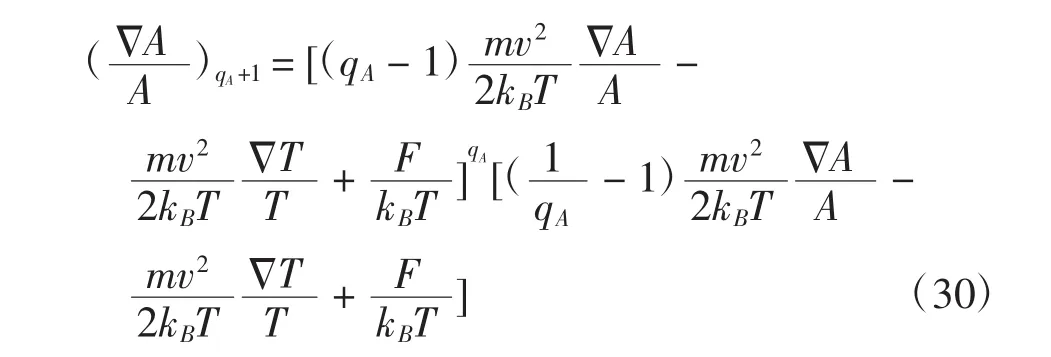
参数qA的方程，虽然不像非广延性q统计和κ统计那样，能够得到关于其参数的简单的数学关系，但从这个方程中，仍可以看到参数qA将系统的温度梯度和外场力F联系起来，表明它们之间的数值关系。因此，参数qA既是反应系统偏离平衡态程度的一个特征量，也是该广义统计的一个核心参量。

6 结语

通过对经典的玻尔兹曼熵的推广，引入不同的参数，得到了不同的广义熵函数，进而得到相应的广义统计。本文详细分析了Tsallis非广延q统计熵、κ统计熵、双参数广义统计熵及Abe熵中的参数。并从广义的玻尔兹曼方程出发，研究了它们各自的物理意义。不同的广义统计的参数都可以看做是它们和经典玻尔兹曼熵之间偏离程度的量度，且这些参数还可以表示出相应的广义统计的适用范围。本研究既可理清不同的广义统计之间的关系，又可为更多的应用领域打开通道。

参考文献：

［1］CHAVANIS P H，VATTEVILLE J，BOUCHET F.Dynamics and thermodynamics of a simple model similar to selfgravitating systems：The HMF model［J］.European Physical Journal B，2005（46）：61-99.

［2］CAMPA A，GIANSANTI A，MORONI D，et al.Classical spin systems with long-range interactions：Universal reduction of mixing［J］.Physics Letters A，2001，286（4）：251-256.

［3］CABRAL B J C ，TSALLIS C.Metastability and weak mixing in classical long-range many-rotator systems［J］.Physical Review E，2002，66：065101.

［4］CHAVANIS P H.Quasi-stationary states and incomplete violent relaxation in systems with long-range interactions［J］.Physica A，2006，365（1）：102-107.

［5］FERMI E.Thermodynamics［M］.New York：Courier Dover Publications，1956.

［6］Robertson H S.Statistical Thermophysics［M］.New Jersey：Prentice Hall，1993.

［7］LANDSBERG P T.Thermodynamics and Statistical Mechanics［M］.Oxford：Oxford University Press，1978.

［8］TSALLIS C，Menes R S，Plastino A R.The role of constraints within generalized nonextensive statistics［J］.Physica A，1998，261：534-554.

［9］TSALLIS C.Possible generalization of boltzmann-gibbs statistics［J］.Journal of Statistical Physica，1988，52：479-487.

［10］TIRNAKLI U，LYRA M L.Critical dynamics of anisotropic Bak-Sneppen model［J］.Physics A，2004，342：151-157.

［11］DU J.Jeans’criterion in nonextensive statistical mechanics［J］.Physica A，2004，335：107-114.

［12］ANDRADE R F S，PINHO S T R.Tsallis scaling and the long-range Ising chain：A transfer matrix approach［J］.Physical Review E，2005，71（026126）：1-8.

［13］TIRNAKLI U，DEMIRHAN D，BUYUKKILIC F.Comparison of the standard statistical thermodynamics with the generalized statistical thermodynamics results for the Ising chain［J］.Acta Physica Polonica A，1997，91（6）：1035-1042.

［14］HUANG X P，ANDEREGG F，HOLLMANN E M，et al.Steady-state confinement of non-neutral plasmas by rotating electric fields［J］.Physical Review Letters，1997，78：875-878.

［15］OU C J，CHEN J C.Nonextensive thermostatistic properties of a q-generalized Fermi system ［J］.European Physical Journal B，2005，43：271-277.

［16］VIGNAT C，NAUDTS J.Stabilily of families of probability distributions under reduction of the number of degrees of freedom［J］.Physica A，2004，350：296-302.

［17］PEREIRA F I M，SILVA R，ALCANIZ J S.Nonextensive effects on the relativistic nuclear equation of state［J］.Physical Review C，2007，76：251-266.

［18］DU J.Nonextensivity and the power-law distributions for the systems with self-gravitating long-range interactions［J］.Astrophysics and Space Science，2007，312：47-55.

［19］DU J.The nonextensive parameter and Tsallis distribution for self-gravitating systems［J］.Europhysics Letters，2004，67（6）：893-899.

［20］DU J.What does the nonextensive parameter stand for in selfgravitating systems［J］.Astrophysics and Space Science，2006，305（3）：247-251.

［21］KANIADAKIS G.Non-linear kinetics underlying generalized statistics［J］.Physica A，2012，296：405-425.

［22］KANIADAKIS G.Statistical mechanics in the context of special relativity［J］.Physical Review E，2002，66（056125）：361-362.

［23］GUO L，DU J，LIU Z.The property of κ-deformed statistics for a relativistic gas in an electromagnetic field：κ parameter and κ-distribution［J］.Physics Letters A，2007，367：431-435.

［24］KANIADAKIS G.Statistical mechanics in the context of special relativity II［J］.Physical Review E，2005，72（036108）：1-14.

［25］GUO L.Physical meaning of the parameters in the twoparameter（κ，ζ）generalized statistics［J］.Modern Physics Letters B，2012，26（1250064）：1378-1388.

［26］KANIADAKIS G.Maximum entropy principle and power-law tailed distributions［J］.European Physical Journal B，2009，70（1）：3-13.

［27］ABE S.A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics［J］.Physics Letters A，1997，224：326-330.