基于曲率流的屏幕空间流体渲染

杨欣

（四川大学计算机学院，成都 610025）

0 引言

在虚拟现实技术日益发展的过程中，流体渲染已逐渐成为一个研究热点。目前，基于网格和基于粒子的流体模拟是计算机图形学的两大分类，而流体作为粒子是更方便地去整合它所处的物理系统的，如每个粒子都有自己的位置、压力、密度、速度等属性，正因为有这些属性使得流体更加真实；；也正是因为如此，平滑粒子流体力学（Smoothed Particle Hydrodynamics,SPH）方法使得我们更难去提取或定义流体的表面，针对基于粒子模拟的流体的渲染方法是很少的，并且大部分都并非实时。

在采用平滑粒子流体力学方法已经模拟出流体的前提下，本文的输入数据为粒子pi的位置xi，甚至也可以包括速度vi和密度ρi，分为四个步骤完成渲染：第一个绘制遍根据位置，表面深度，厚度得到深度图；第一个绘制遍生成厚度图；第三个绘制遍采用曲率流进行对表面深度平滑处理；第四个绘制遍渲染场景天空盒背景；最后一个整合绘制遍进行光照处理。

1 表面

通常来说，流体的表面是定义在世界空间下，要么是作为网格直接定义[1]，要么是用Marching Cubes多边形化之后定义的隐式表面[2]。但是实际上每一帧流体的移动和渲染都取决于视点，故在视点坐标系下去定义表面是更利于有效计算的[3]，故本文的一个核心在于是在视点空间进行渲染处理，如图1。

图1 表面

1.1 点精灵

点精灵是使用片元着色器渲染的OpenGL点，运行的时候考虑点内的片元坐标，其坐标是两维向量gl_PointCoord，可以任意使用这个变量，特别之处在于一个顶点也可以贴纹理。

点精灵的局限在于一个顶点缩放都必须是矩形，并且其最大最小值是有范围的，故如果要使点精灵表现为球体，通过公式（1）和（2）计算得到的N的长度如果大于1，则discard来将立方体变为球体：

1.2 表面深度

每一帧的摄像机位置视点决定了流体的表面，将每一个粒子渲染为球体，通过硬件深度测试来获取每个像素后面离近平面最近的深度值作为表面值。为了能够获取视点下流体的表面，我们采用点精灵技术，在片元着色器中将深度写入到离线缓存。我们仅仅需要存储深度即可，而不需要存储颜色，而深度信息则是后续的平滑处理以及法线计算所需要用到的输入数据。渲染的深度图如图2、图3、图4。

图2 4000粒子深度图

图3 8000粒子深度图

图4 16000粒子深度图

2 曲率流平滑处理

对流体表面的平滑处理最常见的方法是高斯模糊及其变体形式，如双向高斯滤波[4]。高斯模糊的平滑方式会使得流体的边缘出现影子，轮廓边缘显得更暗；双向高斯滤波处理对边界的处理会好很多，但是不可分割的，因此代价消耗比较昂贵。

本文采用曲率流（curvature flow）[5]实现了在屏幕空间平滑流体的表面。该方法的出发点在于当流体流动的时候，主要处理粒子间的曲率来形成平滑且连续的表面。曲率流沿着它的法线方向演化成一个表面，其演化速度取决于表面的平均曲率大小和正负。虽然我们只操作垂直于视点平面的z轴方向，但我们可以通过对于曲率的比例，改变z值来达到我们想要的平滑效果。因此，我们如下定义：

其中，t是平滑迭代次数，H是平均曲率；H平均曲率定义为表面的单位法向量的散度。

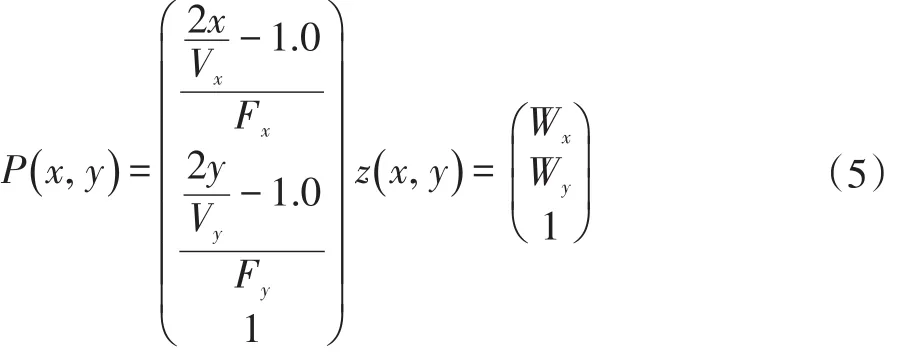
其中，通过投影矩阵的逆矩阵可以将一个粒子映射到视点空间下的P；Vx，Vy是视口参数；Fx，Fy分别是x和y方向上的焦距。

其中，

法线是由P在x和y方向上的导数的叉乘所得到。为了简化公式（6），我们忽略P依赖于视点位置Wx，Wy的因素式，实际上此因素式的作用微不足道，故我们可以得到单位向量公式如下：

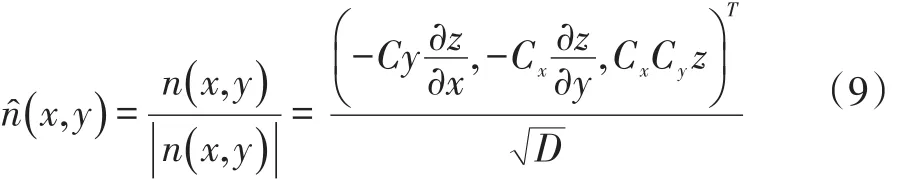
由于z是x，y表示的函数，散度的z分量总是零，再结合公式（4），推出H的公式：

其中，

为了防止流体边缘表面的不连续混合，在深度会发生骤变的两像素边界以及屏幕的边界处，我们强制使得空间散度为零。

每个迭代，公式（3）的简单欧拉积分都用来修改了z值，z值的空间散度用有限差分计算而得。迭代的次数依赖于想要的平滑效果所设定，迭代次数越多，效果更平滑，但同时计算量也会更大[4]。

3 厚度

厚度是用来表示每个像素点处的流体量。为了达到这种半透明渐变效果，针对每一个像素，计算得出摄像机和最近的透明物体的数量。在绘制的时候和第一个绘制遍一致，但不同的是需要开启混合，存储厚度到帧缓存中，而不是之前的深度。开启混合的作用则是去累加屏幕中每个位置的流体量。开启深度测试，保证只渲染在场景中最前方的流体。此厚度的有效性是在粒子没有重叠的情况下成立，而正好平滑粒子流体力学（SPH）模拟方法能保证这一点。

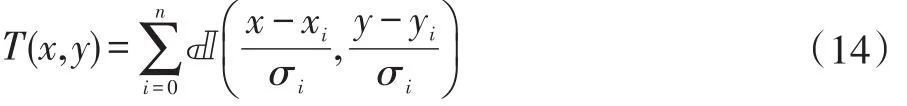
4 天空盒背景

实现天空盒背景的主要技术是使用立方体映射纹理技术，而使用天空盒背景的目的在于体现流体的反射效果。

首先，立方体映射纹理是一种特殊类型的纹理，用于环境映射，使用6个正方形的并且大小相同的子纹理作为立方体映射的6个面，如图5。通过将一个纹理绑定到gl_TEXTURE_CUBE_MAP纹理目标，并在gl_TEXTURE_CUBE_MAP目标上调用glTexStorage2D（）可以为立方体映射纹理分配存储空间。分配存储空间后，立方体映射用6个特殊目标的集合表示，分别是GL_TEXTURE_CUBE_MAP_POSITIVE_X、GL_TEXTURE_CUBE_MAP_NEGATIVCE_X、GL_TEXTURE_CUBE_MAP_POSITIVE_Y、GL_TEXTURE_CUBE_MAP_NEGATIVE_Y、GL_TEXTURE_CUBE_MAP_POSITIVE_Z，GL_TEXTURE_CUBE_MAP_NEGATIVE_Z。

图5 Cubemap六张纹理图

在立方体映射中采样的时候，使用的纹理坐标是三维且看作来自原点的方向，方向指向用来读取纹理的立方体映射表面的位置。立方体映射对于表示周围环境、光和反射效果是很完美的。在第四个绘制遍的时候绘制出的天空盒背景，在最后一个绘制遍整合的时候，在片元着色器中可以通过内置函数reflect（Inci⁃dentLight,Normal）得到的结果去采取立方体映射的纹素来达到反射的效果。

5 渲染

在最后一个绘制遍，将之前绘制遍渲染的帧缓存（深度图、厚度图、法线图等）做最后的整合处理，来得到最终的效果。本绘制遍主要做光照处理，其中包括冯氏光照和菲涅尔反射。

5.1 冯氏光照模型

冯氏光照模型主要由环境（Ambient）光照、漫反射（Diffuse）光照、镜面（Specular）光照构成。

环境光照使物体永远不会是完全黑暗的，在现实生活中环境光只是平行光找到其他物体上；漫反射光照和观察者的角度无关，但其是冯氏光照模型最显著的组成部分，决定了物体的主要颜色；镜面反射光照是模拟有光泽物体上面出现的亮点，使其更倾向于光的颜色，此光照与视角和材质光泽度（Shininess）有关。结合三种光照元素，构成的冯氏光照公式如下：

图6 4000粒子，30次曲率流迭代

其中，AStrength是环境光系数；LightColor是光的主颜色；Ambient是环境光分量；Normal是物体表面的法线；LightDir是光的方向，即物体到光源的向量；Dif⁃fuse是漫反射分量；SStrength是镜面强度；ViewDir是物体到眼睛的向量；ReflectDir则是LightDir基于Nor⁃mal的反射向量；Shininess是高光的反光度。

5.2 菲涅尔反射

菲涅尔反射所反映的现象在于流体表面在棱角尖锐处反射更强烈。换言之，视线垂直于表面时，反射较弱；视线飞垂直表面时，夹角越小，反射越明显。在渲染中采用了近似处理，公式如下：

其中，θ是入射角；R0是反射率；cosθ是法线和视线向量的点乘。

6 实验结果

实验针对平滑粒子流体力学模拟出来的流体，仅仅针对其渲染做出实验。实验控制两个变量，一是粒子数量，一是曲率流平滑处理迭代次数。针对这两个变量的取值，分别做了6个实验，如图6-11。

图7 4000粒子，60次曲率流迭代

图8 8000粒子，30次曲率流迭代

图9 8000粒子，60次曲率流迭代

图10 16000粒子，30次曲率流迭代

从上述实验可以看到，粒子数量越多，渲染的流体密度更为密集，稀疏度更真实；曲率流迭代次数越多，流体表面更加光滑，颗粒感越不明显。

7 结语

本文针对粒子化流体进行实时渲染，采用了点精灵将粒子球体化，使得可以简单地捕捉流体的表面；进一步通过可以控制迭代次数的曲率流平滑处理流体，使其更加真实；最后为流体增加天空盒和菲涅尔反射效果，结合冯氏光照模型渲染处最终效果。布料模拟方法采用预计算处理弹簧质点模型数据。在兼顾真实感的同时，对绘制效率也有较好的提升，能够被运用于电子游戏，电影动画产业中。但同时，本文未对流体加入噪声、焦散、阴影等更为细节的研究，需要在接下来的工作中进行研究和完善。

参考文献：

[1]Stora D,Agliati P,Cani M,et al.Animating Lava Flows[C].Graphics Interface,1999:203-210.

[2]Lorensen W E,Cline H E.Marching Cubes:A High Resolution 3D Surface Construction Algorithm[J].International Conference on Computer Graphics and Interactive Techniques,1987,21（4）:163-169.

[3]Muller M,Schirm S,Duthaler S,et al.Screen Space Meshes[C].International Conference on Computer Graphics and Interactive Techniques,2007:9-15.

[4]Aurich V.,Weule J.（1995）Non-Linear Gaussian Filters Performing Edge Preserving Diffusion.In:Sagerer G.,Posch S.,Kummert F.（eds）Mustererkennung 1995.Informatik Aktuell.Springer,Berlin,Heidelberg.

[5]Malladi R.,Sethian J.A.（1997）Level Set Methods for Curvature Flow,Image Enchancement,and Shape Recovery in Medical Images.In:Hege HC.,Polthier K.（eds）Visualization and Mathematics.Springer,Berlin,Heidelberg.