基于升轨方式的低轨卫星主动离轨处置策略

张国云 樊恒海 蔡立锋 张国龙 王大鹏 祝俊淞

(西安卫星测控中心，西安 710043)

随着低轨卫星数量的逐年增加，有限的近地空间资源日趋紧张，在轨运行卫星碰撞概率不断增大，碰撞预警和规避控制日趋常态化。对已结束在轨服务或已退役的卫星进行主动离轨处置，不仅可以减小其与在轨正常工作卫星可能的碰撞风险，确保当前在轨运行卫星及后续发射与运行任务的安全，同时还可释放占用的空间资源，为其他卫星及后续卫星留出轨道位置[1-4]。

目前，高轨卫星的主动离轨处置主要通过抬高轨道高度(升轨方式)或者轨道高度与倾角联合控制等方式，将退役卫星推入坟墓轨道，进行钝化处置[2]。低轨卫星的主动离轨处置主要通过降低轨道高度，依靠大气阻力作用使卫星再入大气层烧毁。然而，采用降轨方式进行主动离轨处置时，存在两方面问题：①随着轨道高度的降低，空间碎片及在轨卫星数量逐渐增加，待离轨低轨卫星会威胁到在轨正常运行的卫星，尤其在轨道高度降低到900 km左右时，空间碎片数量发生跃变，发生碰撞的概率大大增加；②根据机构间空间碎片协调委员会(IADC)编订的《IADC空间碎片减缓指南》，低轨卫星在任务完成后主动离轨，需要在25年内再入大气层烧毁[5]。对于轨道高度大于900 km的低轨卫星，若在大气阻力作用下使其自然衰减，需要花费上千年的时间，大大超过25年以内的要求。若采用升轨方式的离轨处置策略，可以避免以上两个问题。对于低轨卫星，升轨方式的离轨处置策略在苏联卫星的核反应堆舱段上应用过，核反应堆舱段从200 km机动到约1000 km的轨道高度，以防止其污染地球环境[6]；而对于低轨整颗卫星的升轨方式主动离轨处置策略，以及后续的协调策略，还未有详细分析。

本文基于卫星长期管理过程中的工程应用实践，提出了升轨方式的低轨卫星主动离轨处置策略。在综合考虑轨道高度、剩余燃料、碰撞风险及离轨后器件在轨寿命考核，以及空间科学试验价值的基础上，进一步提出了“保能源、保燃料、保测控”的协调策略。最后，以已退役的某低轨卫星为例，对提出的离轨处置策略进行了验证。

1 主动离轨处置策略

对于低轨卫星在完成任务后进行离轨机动，IADC仅给出了原则性的处理要求与建议，至于目标轨道参数，可由各卫星所属机构自行研究决定。由于整星采用升轨方式进行离轨控制无经验可循，因此，目标轨道区域主要根据空间碎片及在轨卫星数量与轨道高度的关系，以及燃料受限情况确定。目标轨道高度确定后，还要确定相应的轨道转移方式。同时，考虑到离轨后空间科学和应用试验的需要，卫星进入目标轨道后，还要有相应的安全处置策略。按照“保能源、保燃料、保测控”的协调策略，提出对离轨后低轨卫星的安全处置策略。离轨处置过程如图1所示。

1.1 离轨目标轨道区域确定

图2给出了在500～1400 km的空间碎片及在轨卫星数量随轨道高度(h)的变化关系。由图2可得，h约为900 km时，空间碎片及在轨卫星数量发生跃变。因而，若将待离轨卫星自h约为900 km向下调整时，降轨控制过程需要消耗较多燃料，若出现燃料不足的情况，将不能完成后续离轨操作，且无法将卫星送至25年陨落地面的轨道上。另外，随着h的不断减小，碰撞的可能性大大增加，会威胁到在轨正常运行的卫星[7]。由此可见，在燃料受限的情况下，应考虑升轨方式，升轨后的轨道高度分布的卫星相对较少，碰撞概率较小。在h低于1200 km的空间中，空间碎片及在轨卫星数量明显较多，当h在1300～1400 km时，空间碎片及在轨卫星数量又有所增加。综合以上，对于h高于900 km的卫星，主动离轨后目标区域范围为h低于1300 km。

1.2 轨道转移方式

根据卫星轨道控制原则和轨道控制动力学特性，为保证偏心率稳定，相邻2次控制时刻的轨道相位差应保证约为180°。实施双脉冲共面变轨最优的方式为霍曼变轨[8]，霍曼变轨在理论上也是圆轨道之间最节省燃料的变轨方式[9]，因而选择霍曼变轨将待离轨卫星转移到目标轨道。

待离轨卫星变轨的基本原理如图3所示，O为地心；R1为离轨前卫星轨道地心距；R2为实际离轨控制后进入的轨道地心距；ΔV1和ΔV2为2次变轨时刻对应的速度增量。在A1对卫星施加第一脉冲速度增量ΔV1，抬高卫星近地点，进入椭圆形的转移轨道，该椭圆分别与两圆相切，切点即为转移轨道的近地点和远地点。卫星沿转移轨道运行至A2，此时A2成为卫星新轨道的远地点，施加第二脉冲速度增量ΔV2，卫星进入目标轨道，变轨结束。

根据霍曼变轨理论，计算可得卫星双脉冲速度增量为[10]

(1)

式中：地球引力常数μ=3.986 005×1014。

实际上，进行卫星离轨控制时，要采用多批次小控制量两脉冲霍曼变轨，逐渐抬高卫星轨道高度，最终达到目标轨道。

1.3 离轨后安全处置策略

考虑到离轨后应急处置和空间科学试验的需要，确定了“保能源、保燃料、保测控”的协调策路。①保能源：采用将太阳电池阵对准太阳的方式保证电能充足；②保燃料：在满足太阳电池阵对日条件下，使卫星按照一定的角速度旋转，构成足够大的角动量，以保持姿态稳定，避免使用喷气控制消耗能源；③保测控：卫星的自旋角速度在一定范围内，以满足卫星的测控条件。“保能源、保燃料、保测控”的要求，互相制约，形成合理的处置策略。

1.3.1 保能源

为便于分析，建立卫星本体坐标系ObXbYbZb和轨道坐标系OoXoYoZo，卫星质心为Ob(Oo)。为保证较好的光照，起旋前，先将卫星本体绕偏航轴负向转动90°，并将两副太阳电池阵驱动到270°后停转，这时太阳电池阵的电池片法线是指向卫星本体的，即轨道坐标系(OoXoYoZo)的-Yo方向(太阳方向)，见图4。太阳电池阵调整后，对着太阳，可确保卫星电能供给。

1)离轨前后飞行状态对比分析

图4(a)表示出了3轴对地稳定飞行过程中卫星运行状态与太阳电池阵的位置关系。在此过程中，卫星本体坐标系中3轴指向与轨道坐标系3轴指向保持一致。在图4(b)中的自旋状态下，卫星绕本体坐标系Xb轴旋转，卫星本体坐标系Yb轴指向卫星飞行方向。

2)降交点地方时漂移对光照条件的影响分析

在轨运行过程中，由于太阳引力摄动，卫星倾角会发生长期的缓慢变化，进而引起降交点地方时漂移。因此，需要计算出目标轨道降交点地方时的变化，判断太阳电池阵光照条件。

1.3.2 保燃料

由自旋刚体定向性和稳定性原理可知：在没有外力矩作用时，当且仅当卫星本体以惯量主轴为转轴时，转轴才具有定向性；当卫星本体自旋轴为其最大惯量主轴或最小惯量主轴时，卫星旋转状态才是稳定的[11]。考虑到实际空间环境的复杂性，且卫星带有太阳翼等挠性附件，分析中不能简单作为刚体处理。进一步根据半刚体卫星自旋稳定原理可知：任何形状的卫星本体，只有绕最大惯量主轴的自旋才具有稳定性。

1)卫星惯量主轴计算与自旋轴确定

利用卫星质量和惯量特性，计算3轴主惯量IXb，IZb，IYb(惯性坐标系在本体坐标系下的投影)，三者最大值即为卫星旋转惯量主轴。根据卫星特点及推力器安装布局，为满足自旋条件，同时考虑将来消旋可能对燃料的消耗，在确保对测控影响较小的前提下，可通过滚动轴喷气使卫星本体绕惯量主轴以自旋角速度旋转，自旋稳定后将卫星推进系统关闭，保证燃料的零消耗。

2)卫星自旋角速度选择原则

根据卫星刚性设计原则，自旋角速度小于等于9 (°)/s，否则存在解体的可能性。为了便于监测自旋角速度，角速度应保持在卫星测量部件测量范围之内，且要考虑地面设备测控跟踪的有效性。卫星自旋后，自旋角速度长期受到外力矩(太阳光压等)的影响并呈增加趋势，因此还要考虑将来对卫星消旋处置的燃料消耗。

3)估算角动量与卫星本体坐标系3轴的夹角

卫星在本体坐标系下的惯量张量及卫星本体惯量参数为

(2)

卫星的角动量H和角速度ωb分别为

(3)

式中：ωXb，ωYb，ωZb为惯性坐标系下3轴角速度在本体坐标系下的投影。

通过计算，可得角动量H与卫星本体坐标系3轴的夹角及H的变化趋势。同时，通过在轨数据验证，自旋轴与最大角动量方向基本一致，卫星本体绕其最大惯量主轴旋转，能够长期保持自旋稳定。

1.3.3 保测控

测控条件需要分析干涉区，当卫星侧旋至干涉区对地时，有可能导致地面遥测信号的短暂失锁和遥控信号的闪锁断，因此要计算闪锁断时间及闪锁断次数。如图5所示，卫星测控信号在卫星本体坐标系-Zb轴方向半球内存在11°左右的2个干涉区，在角速度为自旋状态下，若自旋角速度为1 (°)/s，闪锁断时间约为11 s。因此，在卫星旋转一周的6 min弧段内将会出现2次闪锁断。

注：最外圈圆外数值表示偏离±Zb轴指向(角度)，单位为(°)；实线圆表示不同指向上的增益，单位为dBi。

图5 测控天线方向图

Fig.5 Pattern of TT&C antenna

2 试验验证结果及分析

根据确定的主动离轨处置策略，对已退役的某太阳同步轨道卫星进行离轨控制。该卫星的轨道高度为1200 km，剩余燃料约32 kg(若按降轨150 km计算，要消耗燃料33 kg，届时将出现燃料不足的情况)，降交点地方时为09:30，陀螺的角速度测量范围为[-2.5，+2.5](°)/s。

2.1 离轨控制效果评估

由于目标区域范围不大于1300 km ，综合考虑节省燃料用于后续空间科学试验的需要，试验时抬升轨道50 km，即轨道高度提高到1250 km，消耗燃料约13 kg(剩余约20 kg)。在该轨道高度分布的空间碎片数量较少，且轨道抬升后卫星轨道高度衰减时间大大增长(见表1)。

在轨道转移时，按两脉冲霍曼变轨实施控制，通过4次两脉冲霍曼变轨，将卫星轨道抬高进入预定高度，控制误差小于1%，剩余燃料能满足后续空间科学试验需要，确保离轨控制的安全性和有效性。离轨控制期间半长轴变化情况见图6。

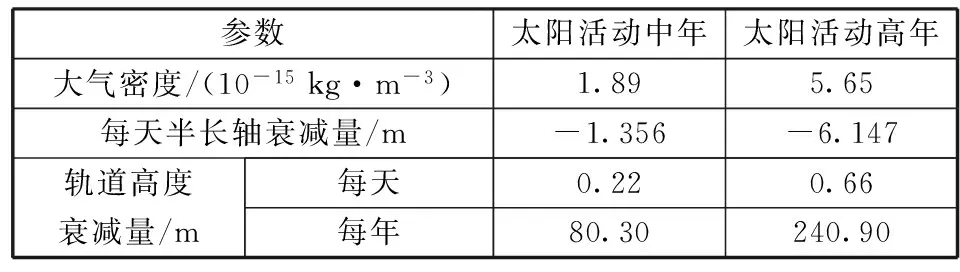
表1 调整后轨道高度衰减估计Table 1 Estimation of orbit altitude attenuationafter adjustment

2.2 离轨后安全处置结果评估

2.2.1 保能源

降交点地方时与太阳光照条件的关系，如图7所示[12]，降交点地方时为00:00或12:00时，轨道平面大致与太阳光平行，而在06:00或18:00时，轨道平面大致与太阳光垂直。卫星太阳电池阵安装在卫星本体坐标系±Yb轴，方向与轨道面平行，因而当降交点地方时为06:00或18:00时，光照条件最好。经过数值仿真，主动升轨至轨道高度1250 km 后，3年内降交点地方时变化曲线见图8，降交点地方时向06:00方向漂移，太阳电池阵入射角逐渐减小，光照条件不断变好，卫星电源供给能力逐步提高。

2.2.2 保燃料

卫星3轴主惯量关系为IXb>IZb>IYb，卫星自旋轴为Xb。通过滚动轴正向喷气使卫星本体绕Xb轴以约1 (°)/s的角速度实现自旋。通过仿真分析，自旋轴角速度越大，章动角越小：自旋角速度约为1 (°)/s时，姿态角基本收敛，而在自旋角速度约为0.5 (°)/s时，姿态角有发散的趋势，如图9～10所示。其中：在图9(a)和图10(a)中，Yb轴和Zb轴的有交叠；在图9(b)和图10(b)中，Xb轴和Yb轴的有交叠。

确定自旋角速度约为1 (°)/s后，计算角动量H与卫星本体坐标系3轴的夹角及其变化趋势。将该卫星惯量张量及卫星本体惯量参数I代入式(3)中，计算可得角动量H与卫星本体坐标系3轴的夹角及角动量H的变化趋势，如图11所示。

由图11(a)～11(c)可见，角动量H与卫星本体坐标系Xb，Yb，Zb轴的夹角趋于1.5°，89.3°，90.4°。卫星不是纯刚体，由于能量耗散，角动量H最终集中在惯量主轴方向，沿Xb轴方向(即角动量H方向)自旋。通过在轨数据验证：自旋轴与最大角动量方向基本一致，卫星本体在绕其最大惯量主轴旋转时，能够长期保持自旋稳定，无需消耗燃料。

由图11(d)可知，角动量H幅值有逐步变大的趋势，当角速度增大到一定门限时，可进行消旋。最大角动量与卫星本体坐标系3轴夹角如图12所示。由于卫星受到外力矩(如太阳光压、重力梯度等)的长期影响，卫星姿态和自旋轴空间指向会随着时间推移发生缓慢变化，因此，对于卫星惯量主轴的确定，要建立相关模型，结合长期演化过程进一步分析。

2.2.3 保测控

卫星在-Zb轴方向半球内存在11°左右的2个干涉区(如图5所示)，干涉区内增益有可能低于-12 dB的指标要求。如图13所示：当自旋角速度为3 (°)/s(卫星自旋一周需要2 min)时，整个跟踪弧段可能经历15次闪锁断(应答机自动增益控制(AGC)门限为-110 dBm)，遥测接收和遥控上行会受到一定的影响，因而，为实现保测控目标，自旋角速度最好小于3 (°)/s。当自旋角速度为1 (°)/s时，闪锁断1次时间约为11 s，卫星旋转一周的6 min内会出现2次闪锁断，按照地面跟踪一轨15 min计算，整个跟踪弧段可能出现5次闪锁断。因此，自旋角速度为1 (°)/s能够保证遥控上行的正确性和遥测接收的连续性，在轨数据与预期一致。

3 结论

本文提出了一种基于升轨方式的低轨卫星主动离轨处置策略，通过对处置策略的分析及成功的工程实践应用，得到如下结论。

(1)对于在低轨中较高轨道的卫星，升轨方式可以较快完成离轨处置，解决单靠大气阻力无法实现25年内再入大气层的问题，为后续进入此轨道的卫星留出轨道空间，同时减少碰撞风险。

(2)目标轨道区域主要根据空间碎片及在轨卫星数量与轨道高度的关系，以及燃料受限情况确定。考虑到节省燃料，轨道转移通过多次霍曼变轨实现。

(3)在保能源中，主要满足太阳电池阵对准太阳；在保燃料中，使卫星按照一定的角速度自旋，构成足够大的角动量，以保持姿态稳定，从而避免使用喷气控制消耗燃料，但需要选择合理的自旋轴空间指向和自旋角速度；在保测控中，卫星的自旋角速度在一定范围内可满足测控条件。

由于卫星受到外力矩(如太阳光压、重力梯度等)的长期影响，卫星姿态和自旋轴空间指向会随着时间推移发生缓慢变化，建立相关模型，确定卫星惯量主轴，结合长期演化过程进一步分析，是后续需要解决的问题。

参考文献(References)

[1] 周静，杨慧，王莉云.中高轨道卫星离轨参数研究[J].航天器工程，2013，22(2)：11-12

Zhou Jing， Yang Hui，Wang Liyun. Study on deorbit elements of medium earth orbit satellites [J].Spacecraft Engineering， 2013， 22(2)： 11-12 (in Chinese)

[2] 罗刚桥.地球静止轨道卫星寿命末期离轨方案研究[J].航天器环境工程，2005，22(2)：73-76

Luo Gangqiao.De-orbit project of GEO satellite in the end of lifetime [J]. Spacecraft Environment Engineering, 2005， 22(2)： 73-76 (in Chinese)

[3] 张玉军，冯书兴.主动式空间碎片清理研究[J].装备指挥技术学院学报，2010，21(6)：78-80

Zhang Yujun， Feng Shuxing. Research on active space debris removal [J]. Journal of Academy of Equipment， 2010， 21(6)： 78-80 (in Chinese)

[4] 雷建宇，张永，郑世贵，等.载人航天器空间碎片防护与减缓设计[J].航天器环境工程，2012，29(4)：388-391

Lei Jianyu， Zhang Yong， Zheng Shigui， et al. Space debris shield and mitigation of a manned spacecraft [J]. Spacecraft Environment Engineering， 2012， 29(4)： 388-391 (in Chinese)

[5] IADC. IADC space debris mitigation guidelines [EB/OL]. [2017-04-21].http://stage.tksc.jaxa.jp/spacelaw/kokusai_utyu/space_debris2/IADC.pdf.

[6] 百度百科.核动力卫星[EB/OL].[2017-04-21].https：//baike.baidu.com/item/核动力卫星/3323111?fr=aladdin

Baidu Baike. Nuclear-powered satellite[EB/OL].[2017-04-21].https：//baike.baidu.com/item/核动力卫星/3323111?fr=aladdin (in Chinese)

[7] 刘林，杨建，王建华.近地轨道空间碎片清除策略分析[J].装备学院学报，2013，24(2)：70-73

Liu Lin， Yang Jian， Wang Jianhua. Research on space debris mitigation strategy in LEO [J]. Journal of Aca-demy of Equipment， 2013， 24(2)： 70-73 (in Chinese)

[8] 杨嘉墀.航天器轨道动力学与控制[M].北京：中国宇航出版社，1995：100-105

Yang Jiachi. Dynamics and control of spacecraft orbit [M]. Beijing： China Astronautics Press，1995： 100-105 (in Chinese)

[9] 肖业伦.航天器飞行动力学原理[M].北京：中国宇航出版社，1995：72-88

Xiao Yelun. Theory of spacecraft flight dynamics [M]. Beijing： China Astronautics Press， 1995：72-88 (in Chinese)

[10] 褚桂柏.航天技术概论[M].北京：中国宇航出版社，2002：312-315

Chu Guibai. Space technology introduction [M]. Beijing： China Astronautics Press， 2002：312-315 (in Chinese)

[11] 樊恒海，魏俊，冀蓉，等.海洋二号卫星重大故障抢救姿态恢复与轨道捕获控制技术[R].西安：西安卫星测控中心，2014：4-10

Fan Henghai， Wei Jun， Ji Rong， et al. Failure to rescue，attitude recovery and orbit capture control techno-logy of HY-2 satellite [R]. Xi’an： Xi’an Satellite Control Center， 2014：4-10 (in Chinese)

[12] 张国云，蔡立锋，黄晓峰，等.近圆太阳同步卫星轨道倾角偏差的影响和调整[J].上海航天，2014，31(2)：37-41

Zhang Guoyun， Cai Lifeng， Huang Xiaofeng，et al. Impact analysis and adjustment of nearly round sun-synchronous orbit satellite injection inclination devia-tion [J]. Aerospace Shanghai， 2014， 31(2)： 37-41 (in Chinese)