利用函数及等价转化法证明二元不等式问题之一

张贵元

(内蒙古包头市萨拉齐第二中学 014100)

(1)若函数f(x)在(0,+∞)上为单调递增函数，求a的取值范围；

又因为f(x)在(0,+∞)上为单调增函数，

所以f′(x)≥0在(0,+∞)上恒成立，

即x2+(2-2a)x+1≥0在(0,+∞)上恒成立，

(2)证法1 由于交换m,n不影响不等式的结构，故可以设m>n.

所以x∈(1,+∞).

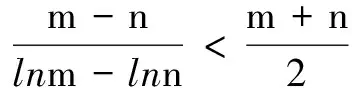
所以只需证明g(x)>2即可.

而g′(x)=

令h(x)=x2-2xlnx-1，x∈(1,+∞)，

所以h′(x)=2x-2(lnx+1)=2x-2-2lnx，

反思与归纳二元不等式有两种形式，一种形式是对于同一个函数的两个自变量而言，另一种形式则是对不同函数的不同自变量而言.利用导数解决第一种形式的二元不等式的基本思想是：把这个二元不等式转化为一元不等式，通过构造函数，然后按照导数研究一元不等式的方法来解决.一般来说，转化的基本思想有两种，一是利用函数的单调性，把不等式转化为一个函数在指定区间上的单调性问题，二是通过"奇次变换"把二元不等式变为一元不等式.

对于第二种形式的不等式，则是转化为不同函数的最值问题加以解决，即证明 .(特别注意：在把不等式转化为一元不等式时，要注意变换的等价性以及变换后函数的定义域.)

参考文献：

[1]韩清海.新课标高中总复习导与练:第一轮[M].广州：新世纪出版社，2016.