数形结合巧解一类多变量最大值的最小值问题

黎金传

(浙江宁波镇海中学 315000)

例1 已知二次函数f(x)=-x2+ax+b(a,b∈R),设M(a,b)为g(x)=|f(x)|在[1,2]上的最大值.

(1)当a=1时，求M(1,b)关于b的解析式；

(2)若对于任意a,b∈R.恒有M(a,b)≥M(a0,b0),求满足条件的所有实数对(a0,b0).

原解(1)当a=1时，f(x)=-x2+x+b,则f(x)在[1,2]上单调递减，故f(x)在[1,2]上的值域为[b-2,b].

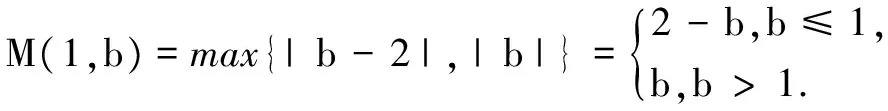
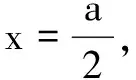
①当a≤2或a≥4时，f(x)在[1,2]上单调，又

f(1)=a+b-1,f(2)=2a+b-4,

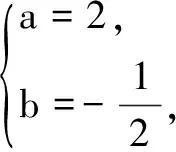
三个不等式同时取到等号的条件为

这与3

图1

图2

解完一道题后经常要对于该题进行反思，首先要想想这道题考察了哪些知识点，是从哪些角度来考察的？你还可以从哪些角度来考虑？其次，该题考查了什么思想方法？以后再运用这种思想方法的时候要注意什么？最重要的是通过该题掌握这一类问题的解法.

把问题推广：g(x)=

例2 (2016浙江高考模拟冲刺(四))已知函数

(1)若b=-2，且函数f(x)在区间[-1,1]上有两个零点，求a的取值范围；

(2)设函数g(x)=|f(x)|在区间[-1,1]上的最大值为M(a,b)，若M(a,b)≥k对于任意的a>1,b∈R恒成立，求k的最大值.

参考文献：

[1]霍正平.一道二元函数最值问题的数形结合巧解[J].数学之友,2011(03).