尺度自适应的加权压缩跟踪算法
李晓行,陈金广,马丽丽, 王明明,王 伟
(西安工程大学 计算机科学学院, 陕西 西安 710048)
0 引 言
目标跟踪是计算机视觉领域中的主要研究内容之一,广泛应用于运动识别、视频监控、视频索引、人机交互等领域中[1].由于目标跟踪面临着光照变化、运动模糊、目标遮挡等挑战因素,因此,其研究仍是重点与难点.目标跟踪算法一般分为生成式模型和判别式模型两大类.
基于生成式模型的目标跟踪算法一般是利用学习得到的目标模型找到具有最小重建错误的图像块,该图像块位置即为目标位置.具有代表性的是Comaniciu等提出的Mean Shift算法[2],该算法利用概率密度梯度估计,通过迭代寻优以找到目标位置,但其对颜色变化较为敏感.Cai等对Mean Shift算法进行了改进[3],将空间直方图和Contourlet直方图进行加权求和,该方法在目标遮挡、旋转、尺度变换等情况下具有较好的鲁棒性.针对Mean Shift算法无法进行尺度自适应更新的问题,Bradski提出了CamShift算法[4],该算法能够自适应地调整目标跟踪区域的大小,具有较好的跟踪效果.IVT算法[5]利用增量主成分分析子空间对目标模型进行描述,能够在线估计目标的外观,从而实现目标跟踪.Mei等[6]提出一种粒子框架下的L1跟踪算法,将跟踪问题看作稀疏逼近问题,该算法在遮挡情况下具有较好的跟踪效果,但计算量较大.
基于判别式模型的目标跟踪算法将跟踪问题看作二元分类问题,将目标和背景区分开来,从而得到目标的位置.Grabner等提出一种在线boosting方法来选择特征进行跟踪[7],仅使用一个正样本和少量负样本更新分类器,易导致跟踪漂移.Babenko等提出了一种多示例学习跟踪算法[8],该算法将训练样本以样本包的形式表示,学习判别模型并训练分类器分离目标与背景,虽然该算法跟踪效果较好,但其易受遮挡及误差的影响.Wang等提出了一种基于超像素的分类模型[9],可以有效解决遮挡问题.Hare等提出使用在线结构化的输出支撑向量机来进行跟踪[10],可以有效地减轻错误标签样本的影响.Zhang等提出了压缩跟踪(CT,Compressive Tracking)算法[11],该算法利用样本的压缩特征来进行分类处理,提高了算法的运行效率,但该算法易受遮挡影响且尺度不能自适应更新.快速压缩跟踪(FCT,Fast Compressive Tracking)算法利用二次定位方法提升了CT算法的运行效率[12],但该算法仍易受遮挡影响且尺度也不能自适应更新.一些学者针对CT算法跟踪准确性不高的问题提出了解决方法[13-16],但这些方法未能实现尺度的自适应更新.
本文提出一种尺度自适应的加权压缩跟踪算法,将判别相关滤波器和尺度金字塔[17]运用于CT算法中,以实现尺度的自适应更新;利用正负样本的巴氏系数对朴素贝叶斯分类器进行加权,使得分类结果更为准确.
1 压缩跟踪算法
压缩跟踪算法是基于压缩感知理论的一种快速鲁棒跟踪算法.压缩感知理论指出,利用一个满足压缩等距性(RIP,Restricted isometry property)条件的随机矩阵对稀疏向量进行随机采样,采样后的低维向量几乎保留了原始向量的全部信息.CT算法正是根据这一理论对高维特征进行采样压缩,这里采用的是Haar-like特征,Haar-like特征是计算机视觉领域一种常用的特征描述算子.其利用一个维数为m×n且满足RIP条件的随机矩阵E,将高维特征向量X(n维)转换到低维特征向量V(m维),其中m远小于n,公式表示为
V=EX.
(1)
其中随机矩阵E为一种非常稀疏的矩阵,第i行第j列元素取值如下:

(2)
Li等[18]证明了当s=O(n)时,矩阵E满足RIP条件,且每一行至多有4个非零元素需要计算,能够有效提高算法的运行速率.
CT算法采用朴素贝叶斯分类器进行分类,利用公式(1)得到样本图像的低维特征向量V=(v1,…,vm)T.假设特征向量中各分量相互独立,且每个样本为目标或背景的概率相同,则朴素贝叶斯分类器的模型如下:
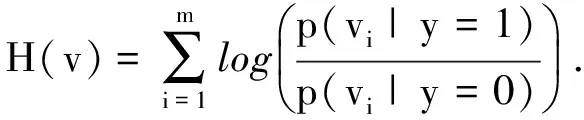
(3)
式中,y=1代表正样本,y=0代表负样本.Diaconis等[18]证明了高维向量的随机投影基本都服从高斯分布,所以可以假设条件概率p(vi|y=1)和p(vi|y=0)服从高斯分布,即
(4)

(5)


(6)
(7)
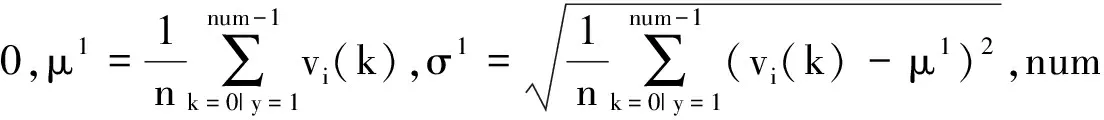
压缩跟踪算法是一种简单高效的实时跟踪算法,在一些简单的场景下具有良好的跟踪效果,但当目标的尺度发生变化时,压缩跟踪算法不能进行自适应的尺度更新,从而导致跟踪结果不准确,且该算法的分类器能力不强.针对上述问题,本文提出一种尺度自适应的加权压缩跟踪算法,将尺度金字塔和判别相关滤波器运用于CT算法中以选取合适的跟踪尺度,并将贝叶斯分类器进行加权处理,以提高算法的鲁棒性和精确性.
2 结合尺度更新的加权压缩跟踪算法
2.1 尺度更新
利用判别相关滤波器及尺度金字塔进行尺度更新,求得不同尺度下的相关滤波器响应,最大的响应值对应的尺度即为当前尺度.假设图像块f具有d维特征描述,即fl(l∈{1,…,d}),这里采用融合方向梯度直方图(fhog)特征,通过计算和统计图像局部区域的梯度方向直方图来构成hog特征,对hog特征进行融合得到fhog特征.可以通过最小化下列代价函数求得最佳相关滤波器h:

(8)
式中,每一维特征fl对应一个滤波器hl,g为与特征f相关联的期望相关输出,λ≥0为正则项的系数.在频域中求解式(8)可得:

(9)

(10)

(11)
式中,η为学习率.新的一帧中,目……标尺度通过求解最大相关滤波器响应y来确定:
(12)
式中,F-1表示傅里叶逆变换,以目标位置为中心提取不同尺度下的样本z,分别提取不同样本的fhog特征,每个样本的fhog特征串联成一个特征向量并构成金字塔特征,将金字塔特征乘以一维汉明窗后作为Z的值.用于目标尺度估计的尺度选择原则为
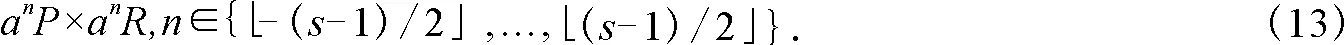
2.2 加权分类器构建
CT算法中构建分类器的所有特征的权值都为1,但正负样本特征的分类能力不同,所以CT算法中的分类器无法突出具有强分类能力特征的重要性,从而导致分类器的分类能力不强.在构建分类器时,考虑到利用正负样本特征相似度的大小对分类器进行加权可以增强分类能力,本文利用巴氏系数来衡量正负样本的相似度.对于连续分布,巴氏系数的表达式为
(14)
式中,B∈[0,1],B越大则两者的相似度越大.根据正负样本的巴氏系数对分类器进行加权.正负样本的巴氏系数越小,分类能力越强,因此给其赋予的权值也就越大.加权后的分类器能够有效地对训练样本的分类能力强弱进行区分,提升了自身的分类能力.加权分类器模型为
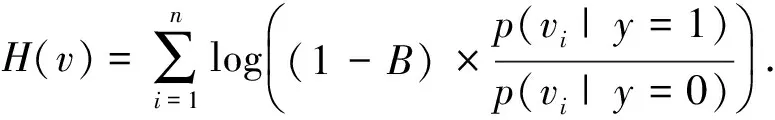
(15)
2.3 算法流程
输入:第t帧图像,上一帧的目标位置It-1及尺度St-1;上一帧的尺度模型At-1,Bt-1;正采样半径rp;负采样半径rn1,rn2;跟踪搜索半径r;正负样的相似度B.
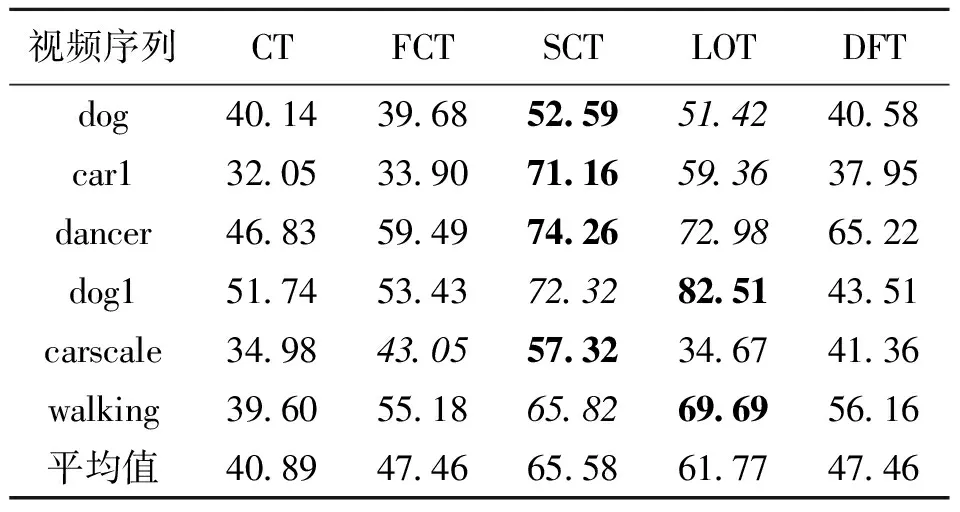
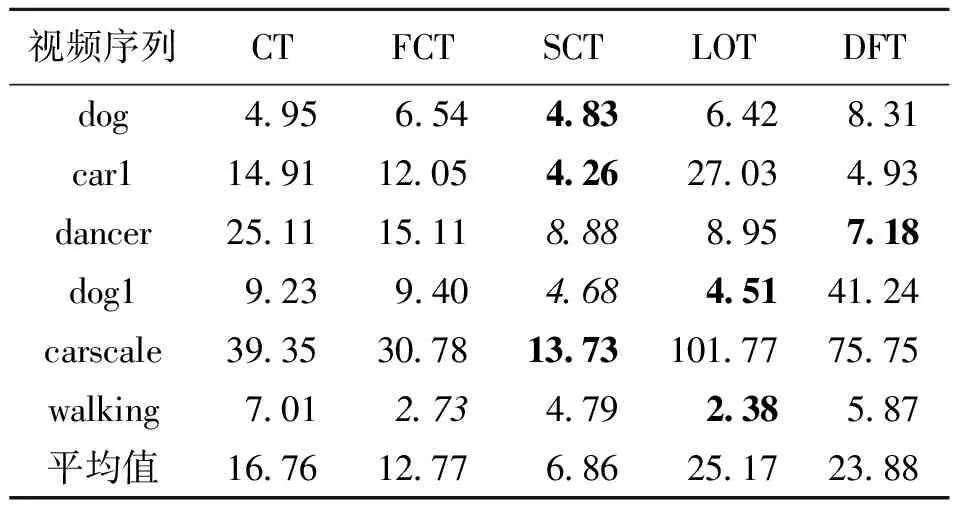
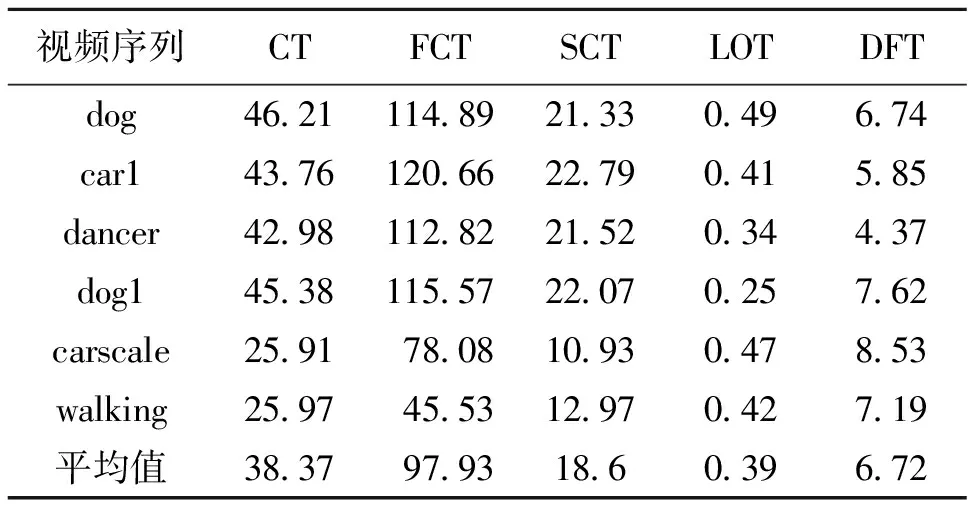
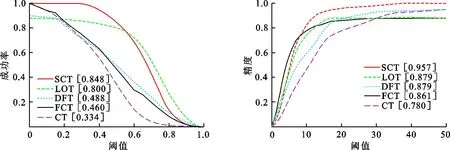
(1) 采集样本集A={s|‖I(s)-It-1‖ (2) 根据式(15)构建分类器H,检测出A中使H响应值最大的样本位置即为目标位置It. (3) 以目标位置为中心,根据尺度及式(13)提取33种不同尺度的样本z. (4) 利用z,At-1,Bt-1、及式(12)计算出相关滤波器响应y. (5) 找到最大的y对应的尺度,并将其作为当前尺度St. (6) 采样正样本集Ap={s|‖I(s)-It‖ (7) 根据It及St提取fhog特征样本f,利用式(10)和式(11)更新尺度模型At,Bt. 输出:当前帧目标位置It及尺度St,尺度模型At,Bt. 为了验证本文算法的有效性,选择与CT[11]、FCT[12]、LOT[20]、DFT[21]4种算法进行比较,选取6组具有尺度变化以及其他挑战因素的视频序列进行测试.实验环境为Intel Core i5双核处理器,2.27 GHz主频,2 GB内存,Windows 7操作系统,MATLAB R2014a. 设置正则化参数λ=0.01,尺度滤波器大小是初始目标大小的两倍,选取尺度间隔为a=1.02的33个尺度值来获得最优尺度,尺度金字塔的学习率η1=0.025,正样本采样半径rp=4,表示在中心点附近以4个像素为半径的圆进行采样,生成45个正样本,负样本采样半径rn1=8,rn2=30,随机采样50个负样本,压缩跟踪算法的学习率η2=0.85,采集候选目标的采样半径r=20,大约生成1 100个候选样本,选取m=100个样本低维特征进行分类器的训练. 为了评价跟踪算法的性能,采用跟踪成功率作为衡量的标准.首先,计算每一帧目标跟踪位置和真实目标位置的重叠率 (16) 式中,rt表示跟踪位置矩形框,ra表示真实目标矩形框,|·|表示矩形框中的像素点个数,S表示跟踪准确度的高低.S越大,准确度越高,当S≥0.5时认为该帧跟踪成功.跟踪成功率由跟踪成功的帧数除以总的帧数来获得.将SCT算法与4种跟踪算法在6种视频序列上的跟踪成功率绘制成表1,每种视频序列跟踪成功率最高的用黑体标注,次高用斜体标注.从表1可以看出,本文算法(图表中简写为SCT)跟踪成功率最高的有4个,次高的有2个,且平均跟踪成功率最高.相比CT和FCT算法,本文算法的跟踪成功率取得了一定的提升.实验结果表明,本文提出的算法具有较好的跟踪效果,有效地改进了CT算法的跟踪性能. 为了更好地评价跟踪算法性能,将平均中心误差作为另一衡量标准.中心误差是指跟踪目标框中心位置和真实目标框中心位置之间的欧氏距离,所有帧中心误差的平均值即为平均中心误差,其值越小跟踪结果越准确.将本文算法与4种跟踪算法在6种视频序列上的平均中心误差绘制成表2,最低的平均中心误差用黑体标注,次低用斜体标注.从表2的实验数据可以看出本文算法在6组视频序列中有3个最低平均中心误差,2个次低平均中心误差,且其6组平均中心误差的期望值最小.实验结果表明,在跟踪精度上,本文算法相较于CT算法取得了一定的改进,算法性能较好. 每秒运行帧数(fps)是衡量算法运行速率的标准之一,fps越大则算法运行速度越快.各算法的fps如表3所示,从表3可以看出虽然本文算法相较于CT算法和FCT算法而言运行速度较慢,但本文算法基本能够满足实时性要求. 表1跟踪成功率 Table 1 Rate of successful tracking % 视频序列CTFCTSCTLOTDFTdog40143968525951424058car132053390711659363795dancer46835949742672986522dog151745343723282514351carscale34984305573234674136walking39605518658269695616平均值40894746655861774746 表 2 平均中心误差 表 3 每秒运行帧数 为了进一步比较各算法的跟踪性能,分别给出各算法OPE下的成功率曲线图以及精确度曲线图,OPE是指将视频序列按照顺序一帧一帧地使用跟踪算法进行处理.图1为5种算法的OPE成功率曲线图,图中的成功率为阈值从0到1变化时各算法跟踪成功帧所占的比例.若使用某一特定阈值下的成功率作为评价准则,则评价结果会具有不公平性,因此采用曲线下面积(AUC)大小来评估算法性能,AUC越大则算法的跟踪成功率越高.从图1可以看出5种算法中SCT算法的AUC最大,CT算法的AUC最小,即SCT算法的跟踪成功率最高. 图2为5种算法的OPE精确度曲线图,图中精确度由中心误差距离满足阈值条件的帧数除以总帧数计算得到,阈值的取值范围为0到50,其单位为像素.不失一般性,选取阈值为20时的精确度作为评价标准,从图2可以看出,5种算法中SCT算法的精确度最高,CT算法的精确度最低,SCT算法较其余4种算法具有较好的跟踪性能. 图 1 成功率曲线 图 2 精确度曲线 Fig.1 Success plot Fig.2 Precision plot 文献[22]将视频的挑战因素分为11类,每个视频序列都具有至少一种挑战因素.为了进一步分析本文算法的性能,给出了3种因素下的算法成功率曲线图和精确度曲线图,3种因素分别为尺度变化、平面外旋转以及平面内旋转,每个曲线图下方标题中括弧内的数字是指该挑战因素下包含的序列组数.从图3可以看出在3种因素下,SCT算法的成功率以及精确度均优于其余4种算法.尤其对于CT算法而言,改进算法有效地解决了目标尺度变化问题且能够较好地解决目标旋转问题. (a) OPE尺度变化成功率曲线(6) (b) OPE平面外旋转下的成功率曲线(4) (c) OPE平面内旋转下的成功率曲线(3) (d) OPE尺度变化精度曲线(6)图 3 尺度变化、平面外旋转、平面内旋转因素下的曲线图Fig.3 Plots for SV, OPR and IPR subsets (e) OPE平面外旋转精度曲线(4) (f) OPE平面内旋转精度曲线(3)图 3 尺度变化、平面外旋转、平面内旋转因素下的曲线图Fig.3 Plots for SV, OPR and IPR subsets 为了更为准确地验证本文算法的有效性,对5种算法的跟踪结果进行比较,选取部分视频序列显示如图4所示.图4(a)为5种算法在car1序列上的实验结果,从图中可以看出:#0027帧时,CT算法和FCT算法均出现了一定的偏移现象,而其余3种算法跟踪较为准确;#0076帧时目标尺度发生变化,SCT算法和LOT算法的跟踪尺度也随之发生变化,而其余算法的跟踪尺度并没有更新;当目标发生尺度变化及光照变化时(#0203帧及#0240帧),只有SCT算法能较为有效地跟踪目标,其余算法均出现了一定的跟踪漂移及丢失现象.实验结果表明本文算法能够进行自适应的尺度更新且跟踪效果较好. 图4(b)为carscale序列上的实验结果,在carscale视频序列中,主要影响因素为尺度变化及部分遮挡.#0159帧时,LOT算法受部分遮挡的影响而丢失目标,在之后的跟踪中没能找回目标;随着目标的尺度变化及遮挡面积增多(#0172帧),DFT算法发生跟踪丢失现象且之后没能找回目标,CT算法和FCT算法虽能跟踪上目标,但跟踪框没有进行尺度更新且存在一定的跟踪漂移现象.从实验结果(#0159帧、#0172帧、#0196帧)可以看出本文算法能够有效处理尺度变化及部分遮挡问题,且比另外4种算法跟踪效果要好. dog视频序列的主要挑战因素为尺度变化和平面内旋转.当目标尺度发生变化时(#0070帧、#0082帧、#0088帧),LOT算法和本文算法的尺度跟踪尺度随着目标尺度的变化而变化,但前者在目标发生旋转(#0070帧、#0088帧)时发生了跟踪漂移现象而本文算法则能有效地跟踪,其他3种算法都没有对目标的尺度进行更新从而导致跟踪结果不准确,如图4(c)所示. dog1视频序列主要有尺度变化和旋转的影响.#0238帧时目标发生一定的旋转变化,LOT算法的尺度更新发生偏差,产生一定的跟踪漂移现象,目标发生尺度变化时(#0919帧),DFT算法发生跟踪丢失现象且之后未能找回目标,CT算法和FCT算法的跟踪尺度都未发生变化,而本文算法和LOT算法能较为有效地跟踪目标,当目标再次发生旋转变化时(#1102帧),LOT算法、CT算法及FCT算法皆发生了一定的跟踪漂移现象,本文算法则能较为准确地跟踪目标,如图4(d)所示.图4的实验结果表明本文算法在尺度更新方面对CT算法进行了有效的改进,且在部分遮挡及旋转的情况下仍能有效跟踪目标. (a) car 1图 4 部分序列跟踪结果Fig.4 Tracking results of some sequences (b) carscale (a) dog (d) dog 1 图 4 部分序列跟踪结果Fig.4 Tracking results of some sequences (1) 针对尺度更新问题,利用相关滤波器进行尺度估计,以目标位置为中心提取33种不同尺度下的样本并求得样本的金字塔特征,将金字塔特征乘以一维汉明窗作为相关滤波器响应的特征输入,使得相关滤波器响应最大的尺度即为当前尺度值. (2) 针对分类器分类能力不强的问题,通过对分类器进行加权来提高分类能力,利用巴氏系数衡量正负样本的判别能力.巴氏系数越大则样本判别能力越差,分类器权值用巴氏系数计算得到,分类能力越大的特征,其权值越大. (3) 在目标尺度发生变化的情况下,本文算法能够实现尺度的自适应更新,而且在部分遮挡,平面内外旋转等情况仍能保持较好的跟踪性能.在时间复杂度方面,本文算法较原有算法有所增加. 参考文献(References): [1] YILMAZ A,JAVED O,SHAH M.Object tracking:A survey[J].ACM Computing Surveys,2006,38(4):1-45. [2] COMANICIU D,RAMESH V,MEER P.Kernel-based object tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(5):564-577. [3] CAI N,ZHU N,GUO W,et al.Object tracking using mean shift for adaptive weighted-sum histograms[J].Circuits Systems and Signal Processing,2014,33(2):483-499. [4] BRADSKI G R.Real time face and object tracking as a component of a perceptual user interface[C]//Proceedings of the 4th IEEE Workshop on Applications of Computer Vision.Princeton,USA:IEEE,2002:214-219. [5] ROSS A D,LIM J,LIN R S,et al.Incremental learning for robust visual tracking[J].International Journal of Computer Vision,2008,77(1-3):125-141. [6] MEI X,LING H B.Robust visual tracking and vehicle classification via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(11):2259-2272. [7] GRABNER H,GRABNER M,BISCHOF H.Real-time tracking via on-line boosting[C]//Proceedings of the British Machine Vision Conference 2013.Dundee,Britain:BMVA Press,2013:47-56. [8] BABENKO B,YANG M H,BELONGIE S.Robust object tracking with online multiple instance learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(8):1619-1632. [9] WANG S,LU H,YANG F,et al.Superpixel tracking[C]//Proceedings of International Conference on Computer Vision.Barcelona,Spain:IEEE,2011:1323-1330. [10] HARE S,SAFFARI A,TORR P H S.Struck:Structured output tracking with kernels[C]//Proceedings of International Conference on Computer Vision.Barcelona,Spain:IEEE,2012:263-270. [11] ZHANG K,ZHANG L,YANG M H.Real-time compressive tracking[C]//Proceedings of European Conference on Computer Vision.Florence,Italy:IEEE,2012:864-877. [12] ZHANG K,ZHANG L,YANG M H.Fast compressive tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(10):2002-2015. [13] 耿磊,王学彬,肖志涛,等.结合特征筛选与二次定位的快速压缩跟踪算法[J].自动化学报,2016,42(9):1421-1431. GENG L,WANG X B,XIAO Z T,et al.Fast compressive tracking algorithm combining feature selection with secondary localization[J].Acta Automatica Sinica,2016,42(9):1421-1431. [14] 李庆武,朱国庆,周妍,等.基于特征在线选择的目标压缩跟踪算法[J].自动化学报,2015,41(11):1961-1970. LI Q W,ZHU G Q,ZHOU Y,et al.Object compressive tracking via online feature selection[J].Acta Automatica Sinica,2015,41(11):1961-1970. [15] 马丽丽,陈金广,胡西民,等.目标跟踪滤波性能的评价准则[J].西安工程大学学报,2013,27(3):364-368. MA L L,CHEN J G,HU X M,et al.Evaluation metrics for filtering performance in target tracking system[J].Journal of Xi′an Polytechnic University,2013,27(3):364-368. [16] 李杰,周浩,张晋,等.粒子群优化的压缩跟踪算法[J].中国图象图形学报,2016,21(8):1068-1077. LI J,ZHOU H,ZHANG J,et al.Compressive tracking algorithm based on particle swarm optimization[J].Journal of Image & Graphics,2016,21(8):1068-1077. [18] LI P,HASTIE T J,CHURCH K W.Very sparse random projections[C]//Proceedings of 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Philadelphia,USA:ACM,2006:287-296. [19] DIACONIS P,FREEDMAN D.Asymptotics of graphical projection pursuit[J].Annals of Statistics,1984,12(3):793-815. [20] AVIDAN S,LEVI DM,BARHILLEL A,et al.Locally orderless tracking[C]//Proceedings of International Journal of Computer Vision,2012,111(2):213-228. [21] SEVILLA-LARA L,LEARNED-MILLER E.Distribution fields for tracking[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Providence,RI,USA:IEEE,2012:1910-1917. [22] WU Y,LIM J,YANG M H.Online object tracking:A benchmark[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Portland,OR,USA:IEEE,2013:2411-2418.3 结果与分析
3.1 参数设置
3.2 数据分析

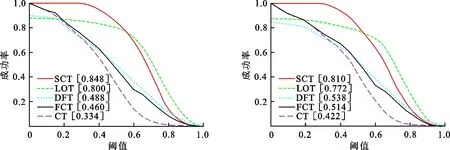
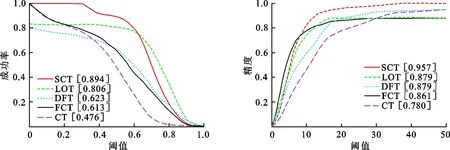
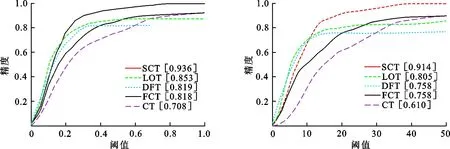
3.3 图示分析





4 结 论

