基于一个水平集函数的多相图像分割方法

,,,

(青岛大学 计算机科学技术学院,山东 青岛 266071)

0 概述

图像分割指在复杂图像中分割出目标图像,其在图像处理、计算机视觉等领域有着重要的研究价值[1]。具有拓扑自适应能力的水平集方法能够有效应对多相分割问题的复杂性[2],是解决图像分割问题的主流方法。变分水平集方法是变分方法和水平集方法的结合,因为其具有集成多种信息和可处理拓扑变化的优点,所以近年来被广泛地应用于多相图像分割的研究领域[3]。

Vese和Chan结合简化的Mumford-Shah[4]模型和水平集方法[3],建立了用于划分2个区域的两相Chan-Vese模型[5],并将其扩展为用于解决分段常值和分段光滑的多相图像分割问题的通用模型。但是,该模型只给出进行区域分割的一般策略,并没有给出进行区域分割的通用公式,如果分割区域很多,就会使能量泛函和相关水平集函数演化方程变得很复杂。

针对上述问题,文献[6-7]提出采用n个函数标记n个区域的Potts模型。为解决函数间的“重叠”和“真空"问题,该模型对相关条件进行约束[8-9]。文献[10-11]提出2种应用于分段常值的多相图像分割模型,其中,一种运用n个将标记函数取值为1或-1的水平集函数,另一种运用标记函数取值为离散常值的一个水平集函数,再通过Lagrange多项式差值获得可以划分多个不同区域的基函数,得到以分段常值为基础的变分水平集图像分割模型,该模型也包含对相关条件的约束[3]。文献[7,12]提出采用n个水平集函数表达2n个区域的标记函数,实现对多个不同区域的划分。文献[13]则采用一个水平集函数标记n(m+1)个区域的多相图像分割模型。但是,以上区域分割策略都需要求解多个函数的极值问题,计算过程比较复杂。

本文采用一个连续变化的水平集函数[14],基于区域竞争策略[15-16]提出m层水平集分割线划分n个区域的方法进行区域特征函数表达,从而构建多相图像分割的变分模型。

1 相关研究

本文引入Heaviside函数为水平集标记函数。并且用Hε(φ)近似Heaviside函数H(φ),即当ε→0时,得到Hε(φ)→H(φ)。由此,根据文献[4-5]有以下结论:

(1)

(2)

基于多相图像分割的区域表达策略,令Ω∈IRn(n=2,3)表示有界开集,f(x):Ω→IR表示在图像区域Ω内的图像强度。运用一个分层的水平集函数表达n个区域的多相图像分割的变分水平集模型[15],其传统表达式可以表示为:

(3)

根据式(3),可以把分段区域求均值的标记函数分为3个部分表达。本文提出区域标记函数的统一化表达式,从而获得多相图像分割的变分模型,其主要思想是使用一个连续函数的多层水平线来划分图像多个不同区域。本文以图1把闭合区域Ω分成5个区域的过程为例。

图1 闭合区间划分示例

(8)

(10)

(11)

(12)

其中,i=1,2,…,m+1。

因此,本文提出多相图像分割模型的能量泛函可以表示为:

(13)

其中,ui=(u1,u2,…,um+1)表示不同区域Ωi内的分段常值,其估计式如式(14)所示。

(14)

当ui被估计后,多相图像分割模型的能量泛函可以表示为:

(15)

由于边缘项函数可以等价表示为:

(16)

因此本文采用的多相图像分割模型的能量泛函可以等价表示为式(17)。

(17)

2 多相图像分割的变分方法

2.1 利用一个水平集函数标记的多相分割模型

本文在变分公式中使用曲线演化的方法对多相分段常值图像进行分割,需要解决在用变分方法进行图像分割时求解极值的问题。本文建立的模型是对文献[16]中引入方法的进一步扩展。下文通过对区域标记函数规律的总结给出标记函数的表达方式:

(18)

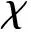
(19)

本文采用的多相图像分割模型,用一个连续函数的多层水平集函数隐含地表示分割边界的集合,从而通过一个水平集函数表达多层水平集的方法,完成多区域图像的分割。因为该模型只涉及一个水平集函数的求解问题,所以大幅减小了计算量。

本文采用交替方向乘子算法(Alternating Direction Method of Multipliers,ADMM)加速算法对该多相图像的变分[17]分割模型进行求解。传统的梯度降算法计算效率比较低,而直接对偶算法也需要对对偶变量用梯度降算法进行求解,Split Bregman算法则需要引用许多辅助变量、惩罚参数以及Bregman迭代参数。针对上述算法的缺点,本文采用ADMM多相图像算法对分割模型进行计算,从而提高计算效率,增强算法稳定性。

2.2 多相分割模型的ADMM算法

当ui的值被计算估计后,基于一个标记函数的多相图像分割模型可以被表达为式(17)。为提高多相图像分割模型[14,18]的计算效率,针对基于一个标记函数的多相图像分割模型,本文采用ADMM算法,从而可以得到多相图像分割模型的能量泛函为:

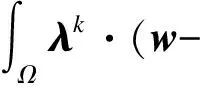
s.t.|w|=1

(20)

其中,λ表示为拉格朗日乘子,用来保证数值计算的稳定性,μ(μ>0)表示惩罚参数。不同于惩罚函数法需要运用惩罚参数来使约束条件得到满足,ADMM加速算法能够使μ不用取很大值的条件来保证约束条件w=φ成立。首先,分别对关于φ和w的能量泛函公式取极小值,再求关于λ的能量泛函公式的极大值[19]。因此,在鞍点处求得的极值的问题满足由交替优化方法得到的关于φ的欧拉拉格朗日方程为:

(21)

为保证标记函数的稳定性,对函数φ(x)加一个约束项为:

φk+1=max(0,min(φk+1,m+1))

(22)

则关于wk+1的广义软阈值公式如式(23)所示。

(23)

对于wk+1,考虑式(20)的约束条件,对其采用以下的方法进行投影:

(24)

然后更新λk+1得:

λk+1=λk+c(wk+1-φk+1)

(25)

本文采用增广拉格朗日投影算法进行求解,步骤描述如下:

1)初始化φ0为水平集函数,w0=λ0=0,k=0。

2)估计ui,并计算Qi(ui),i=1,2,…,q。

3 数值实验

本文实验的平台是PC机:Intel(R) Core (TM) i5 Duo CPU @3.30 GHz 3.30 GHz,内存4 GB,编程运行环境:Matlab R2010b。针对本文多相图像分割模型,采用GDM、DDM、SBM和ADMM算法进行实验。本文选择其中部分图像进行展示。图2是实验的原始图像。图3给出了图2(b)中几何图像区域分割的结果,其中:图3(a)为采用GDM算法的区域分割结果;图3(b)为采用DDM算法的区域分割结果;图3(c)为采用SBM算法的区域分割结果;图3(d)为采用ADMM算法的区域分割结果。可以看出,与其他3种算法相比,ADMM加速算法可以更好地保持几何图像的分割边缘,从而得到更准确的分割结果。图4为对图2中原始图像采用4种算法进行图像分割,得到以不同颜色轮廓线划分不同区域的结果。从彩色图像的分割结果中可以看出,ADMM算法与其他3种算法分割效果类似。

图2 原始图像

图3 几何图像基于不同算法的区域分割结果

图4 彩色图像基于不同算法的分割结果

本文从4幅原始图像中选择图2(a)和图2(d)2幅图像分别加上参数ran分别为0、5、10、15的随机噪声,然后选择传统GDM算法和ADMM加速算法进行对比实验。图5～图8分别为GDM算法和本文算法的实验结果,从中可以看出噪声的改变以及2种算法不同的处理效果。图5、图6为遥感图像加入不同噪声时2种算法的分割结果。通过对比可以看出,在灰度图像的分割过程中,ADMM算法比GDM算法具有更强的鲁棒性。图7、图8为建筑图像加入不同噪声时2种算法的分割结果。

图5 采用GDM算法分割加入不同噪声灰度图像的分割结果及其曲面网格图

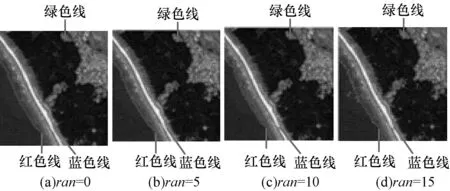
图6 采用ADMM算法分割加入不同噪声灰度图像的分割结果及其曲面网格图

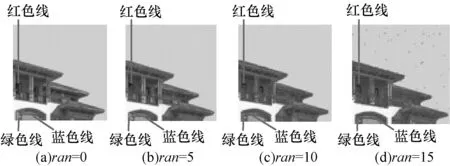
图7 采用GDM算法分割加入不同噪声彩色图像的分割结果及其曲面网格图

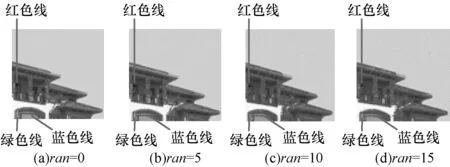
图8 采用ADMM分割加入不同噪声彩色图像的分割结果及其曲面网格图

通过对比可以看出,在彩色图像的分割过程中,ADMM算法比GDM算法也具有更强的鲁棒性。通过以上实验可以看出,ADMM算法与传统的算法相比,可以得到更好的分割结果。并且,本文的ADMM算法与传统的GDM算法相比,具有更强的鲁棒性。本文在采用红、绿、蓝3种不同颜色曲线表示在不同区域的分割线来划分出多个区域。

对原始4幅图像分别采用传统GDM、SBM、DDM和ADMM算法分割,比较能量泛函达收敛时所需要的迭代总次数以及迭代总时间,结果如表1所示。从中可以看出,无论从每步迭代时间、迭代总时间,还是收敛次数,本文ADMM算法的性能均较好,这很大程度上取决于ADMM快速算法简单的差分格式。

表1 不同分割方法迭代次数和计算时间对比

4 结束语

本文利用基于一个函数的多层水平集标记方法对图像多个区域进行标记,并采用增广拉格朗日算法ADMM实现多区域图像的分割,从而简化了计算步骤,提高了多相图像分割的计算效率,同时保证了多相分割方法的鲁棒性。此外,水平集方法非常灵活,在分割过程中可引入不同类型的信息(边界、区域、形状),由于灰度和彩色图像中都包含丰富的不可预测的复杂信息,因此本文方法可有效解决图像分割问题。下一步工作是把基于一个标记函数的分割模型应用于3D或曲面上的多区域图像分割,并将其推广为多区域图像运动分割的变分模型。

[1] 高慧芳,杨 明.一种改进的凸变分水平集模型在图像分割中应用[J].现代电子技术,2017,40(11):72-75.

[2] KEEGAN M S,SANDBERG B,CHAN T F.A multiphase logic framework for multichannel image segmentation[J].Inverse Problems and Imaging,2017,6(1):95-110.

[3] 郭振波.基于变分水平集方法的多相图像分割研究[D].青岛:中国海洋大学,2008.

[4] ESEDOGLU S,TSAI Y H.Threshold dynamics for the piecewise constant Mumford-Shah functional[J].Journal of Computational Physics,2006,211(1):367-384.

[5] CHAN T F,VESE L A.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.

[6] CHAN T F,VESE L A.An active contour model without edges[C]//Proceedings of International Conference on Scale-space Theories in Computer Vision.Berlin,Germany:Springer-Verlag,1999:141-151.

[7] SAMSON C,BLANC F,AUBERT G,et al.A variational model for image classification and restoration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(5):460-472.

[8] SAMSON C,BLANC F,RAUD L,et al.Two variational models for multispectral image classification[C]//Proceedings of International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition.Berlin,Germany:Springer-Verlag,2001:344-358.

[9] 王 靖,潘振宽,郑永果,等.基于Potts模型的隐式曲面上的图像分割方法[J].计算机应用研究,2014,31(9):2873-2877.

[10] LIE J,LYSAKER M,TAI X C.Piecewise constant level set methods and image segmentation[C]//Proceedings of International Conference on Scale Space and PDE Methods in Computer Vision.Berlin,Germany:Springer-Verlag,2005:573-584.

[11] LIE J,LYSAKER M,TAI X C.A binary level set model and some applications to Mumford-Shah Image segmenta-tion[J].IEEE Transactions on Image Processing,2006,15(5):1171-1181.

[12] 王君伟,刘利雄.基于水平集的局部自适应图像分割方法[J].中国科技论文,2017,12(8):895-899.

[13] CHUNG G,VESE L A.Energy minimization based segmentation and denoising using a multilayer level set approach[C]//Proceedings of EMMCVPR’05.Berlin,Germany:Spring-Verlag,2005:439-455.

[14] BRESSON X.A short guide on a fast global minimization algorithm for active contour models[J].EURASIP Journal on Image and Video Processing,2014,7:16.

[15] 刘花香,方江雄,肖 静,等.基于全局凸优化变分模型的快速多相图像分割方法:CN104835168A[P].2015-08-12.

[16] CHUNG G,VESE L A.Image segmentation using a multilayer level-set approach[J].Computing and Visualization in Science,2009,12(6):267-285.

[17] 方江雄.基于变分水平集的图像分割方法研究[D].上海:上海交通大学,2012.

[18] 张 勇,刘宏哲,李 青.基于结构张量的GrabCut图像分割算法[J].计算机工程,2017,43(8):258-265,271.

[19] 端金鸣.基于变分水平集方法的通用模型和快速投影算法研究[D].青岛:青岛大学,2014.