基于Hubness与类加权的k最近邻分类算法

,

(湖南大学 信息科学与工程学院,长沙 410082)

0 概述

随着数据采集技术的发展和互联网的深入,应用领域中的数据越来越呈现高维化趋势。相较于低维数据,各种机器学习方法和任务在高维数据上会面临严重的挑战,例如:数量众多的特征属性之间存在大量冗余和相关性,明显违背贝叶斯建模的基本独立性假设[1];维数增加所带来的样本间距离的集中化,减弱了各种距离指标反映相似性差异的有效性,使得包括k最近邻(k-Nearest Neighbor,kNN)分类和聚类等不能有效地应用于高维数据[2]。这些在数据挖掘和机器学习领域由高维特征空间所带来的各种困难与挑战,统称为维数灾难。

文献[3]探索维数灾难的一个新方向:Hubness。假设Nk(x)为数据集D中样本x出现在其他样本的k最近邻列表中的次数,Hubness现象指在高维数据空间中Nk(x)的分布呈现明显的右偏态,即一些样本点,或非常频繁地作为其他样本的k最近邻(hubs),或很少成为其他样本的k最近邻(anti-hubs)。在文献[3]之后,一些Hubness-aware的kNN和聚类方法相继被提出,都从Hubness这一全新的角度切入解决方法在应对高维数据时的低效性问题。然而,上述方法都没有考虑一个普遍存在的情形:在现实中,许多高维数据往往也是类不平衡的,如文本分类、生物医疗和图像分类等。由于标准的机器学习方法通常以最小化训练错误为目标,少数类样本的稀少使得从不平衡数据中学习的分类器往往忽略少数类的概念信息,从而趋向将所有未知样本预测为大数类[4-5]。此外,已有方法对高维不平衡数据进行处理时,一般先使用各种降维技术以减少数据维度,然后在降维后的数据上应用类不平衡技术以纠正分类器的预测倾斜[6-7]。该做法的不足之处是其进行降维时可能损失原始数据信息。

本文针对Hubness现象,结合类加权技术,提出一种能有效应用于高维不平衡数据分类的HWNN算法,并在实验中将其与已有kNN分类算法进行性能比较。

1 相关工作

近年来,不平衡问题在学术界和工业领域引起了广泛关注,为了解决不平衡问题,许多新的算法被提出,这些算法可以分为2类:数据水平方法和算法水平方法。数据水平方法通过引入新的少数类样本或移除一部分大数类样本,以减轻原始数据的类不平衡分布,该方法的优点是其通用性,即不依赖于任何具体的分类算法;缺点是对于具体的不平衡问题,其可能达不到满意的效果。算法水平方法尝试修改已有的标准机器学习算法,以得到更适应于不平衡数据学习的归纳偏置。例如,在决策树[8-9]中使用类不平衡不敏感的分裂准则,修改叶节点标签的可能性估计;在SVM[10-12]中,赋予少数类样本更高的惩罚因子,修改核函数以校正倾斜的类边界。此外,为了处理不平衡数据的学习问题,许多基于基本kNN分类规则[13-14]的新型分类算法被提出,它们所采用的一个基本策略是向少数类中引入显式的偏置,如样本加权[15]和类加权[16]等。

为了更好地解决不平衡问题,一系列Hubness相关的分类算法被提出[17-21]。与传统k最近邻算法不同的是,Hubness相关算法通过k最近邻列表统计训练样本的Nk,测试点通过其k最近邻的Nk在每个类中的分布进行分类。与传统kNN算法和权重kNN算法相比,Hubness相关算法可以有效提升分类精度。

HW-kNN[22]引入GNk(x)和BNk(x)分别表示Nk中与样本x同类和异类的次数,Nk(x)=GNk(x)+BNk(x),算法还为kNN列表引入权重系数e-(BNk(xi)-μBNk)/σBNk,其中,μBNk和σBNk分别为训练集样本中BNk(x)的平均值和方差。算法通过降低BNk(x)较大样本的权重,消除了样本在分类中可能产生的负面影响。该算法虽然在一定程度上减少了由BNk(x)错误匹配所带来的影响,但是,样本拥有较高的BNk(x)值时,也可能拥有较高的GNk(x)值,降低样本权重值时也会损害由GNk(x)所带来的正确分类信息。

(1)

其中,λ为拉普拉斯平滑因子,通过实验经验选取,本文设置其值为2。

通过联合所有xi∈D(x)的概率求出样本x所属类概率分布。在高维数据下,相较于传统的kNN和HW-kNN算法,NHBNN算法在精度上有较好的提升。然而,虽然在高维不平衡类数据下NHBNN算法总体分类精度较高,但其在少数类上分类精度却较低。对于高维不平衡类数据而言,尤其是少数类,典型分类学习注重的是针对每一类的分类精度,而不是不区分类别的总体精度。

2 HWNN算法

针对实际应用中普遍存在的高维不平衡数据,本文提出的HWNN算法结合Hubness-aware和类加权的方式,分别应对由高维带来的Hubness和由类不平衡带来的预测倾斜问题。

2.1 基于Hubness的kNN分类

最近邻方法基于一个简单的假设,即邻近的样本点通常属于相同的类。kNN分类算法利用该假设,将一个未知样本的类标签预测为它的kNN中出现次数最多的类别,即对于一个测试样本xt,其kNN分类决策dck(xt)如下:

(2)

其中,m是类别的数目,E(yi,c)是一个指示函数,若yi=c,c∈{c1,c2,…,cm},则E(yi,c)返回1;否则,返回0。

为了减少高维数据中由hubs所带来的潜在负面影响,采用基于Hubness的策略,考察每个训练样本的k发生中属于各个类上的比例,以此作为其成为测试样本的k最近邻时对每个类的支持度。

假设xi为当前训练样本,Nk(xi)和Nk,c(xi)分别为其k发生和在c类样本上的k发生,则xi作为c类样本k最近邻的概率为Pk,c(xi),其计算公式如下:

(3)

由式(3)可以看出,当xi的k发生中作为c类样本k最近邻的比例较高时,表示xi的近邻领域中会频繁出现c类的样本。因此,如果xi作为一个测试样本的k最近邻,则其对该测试样本预测为c类有较高的支持度。

通过式(3)得出,测试样本xi的k最近邻对xt预测为c类的支持度和如下:

(4)

xt被预测为cj类的概率可表示为:

(5)

将式(5)代入式(2),得到考虑样本k发生发布下的新kNN决策规则:

(6)

需要指出的是,传统的kNN决策只能得到预测标签值,若要取得在各个类上的预测概率,需要结合距离加权等方式。

然而,运用式(3)对xi在c类样本的k最近邻中的概率进行估计时,需要Nk(xi)具有足够多的统计次数,否则,通过频率估计概率将缺乏可靠性。在高维数据空间中,hubs点挤占了大量的k最近邻关系,同时使得一部分样本(包括anti-hubs点)很少成为其他点的k最近邻。图1所示为最近邻关系示意图,其中A和D的高k发生使得B、E、C的Nk(x)均为0。

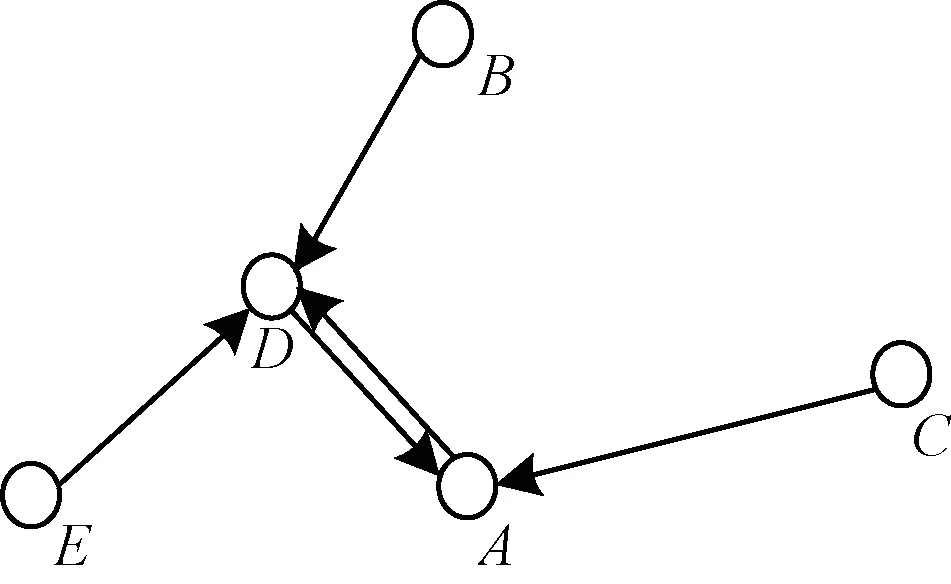
图1 k=1时的k最近邻关系

针对图1中的情况,引入一个阈值参数θ作为经验影响因子,本文将其设置为3。对于Nk(xi)<θ的数据样本,利用样本xi所属类中所有样本的k发生和在c类样本上的k发生来计算Pk,c(xi),计算表达式如下:

(7)

其中,yi表示样本xi类标签,(x,y)∈(X,Y)|y=yi表示所有与xi同类的样本。

综合式(3)和式(7),Pk,c(xi)可表示如下:

(8)

2.2 类加权

在类不平衡数据中,由于少数类数目稀少,一个样本成为少数类样本k最近邻的次数远小于其成为大数类样本k最近邻的次数,因此根据式(8)计算Pk,c(xi)时,其在少数类上的值远小于其在大数类上的值,进而导致式(6)更偏向将测试样本预测为大数类。

为了纠正该倾斜预测,引入类权重如下:

(9)

其中,wc为c类的权重,nc、nmin分别为c类和最小类样本的数目,α为一个缩放因子,值由经验确定,本文将其值设置为常数2.5。

由式(9)可以看出,类样本的数目越多,所获得的类权重越小;反之,获得的类权重越大。因此,本文将类权重加入至样本的k发生统计中。令RN(xi,k)表示xi的k发生列表,对于样本xi,基于类加权的Nk和Nk,c计算表达式如下:

(10)

(11)

其中,y为样本x的类标签,wy为依据式(9)计算出的类权重因素。

可以看出,式(11)使用的加权方式将提升样本在少数类上的k发生。

2.3 HWNN算法流程

HWNN算法的具体描述如下:

算法基于Hubness和类加权的kNN分类算法

输入训练数据集D,近邻参数k,阈值θ

输出测试样本的类标签预测概率

/*预处理阶段*/

1.统计D中每类样本的数目nc,根据式(9)计算各类的权重;

2.计算D中每个样本的k最近邻;

3.根据式(10)和式(11)统计D中每个样本的k发生和其在各个类上的k发生;

4.根据样本的k发生和θ大小,使用式(8)计算得到D中每个样本对各类的支持度;

/*测试阶段*/

5.找到测试样本xt在D中的k最近邻;

6.根据式(4)和式(5)依次得到xt属于各类上的置信度、预测概率。根据式(6)得到xt的最终预测标签。

3 实验结果与分析

3.1 对比方法

选用3种已有的k最近邻分类方法:传统的k最近邻(kNN),基于Hubness的权重k最近邻(WNN),基于Hubness的朴素贝叶斯最近邻(NHBNN),与HWNN算法进行比较。为了考察类加权和基于Hubness分别在HWNN应对高维不平衡数据中所发挥的作用,引入加权的k最近邻分类方法WNN(即一个k最近邻的投票权重由式(9)决定)和无类加权的基于Hubness的k最近邻分类方法HNN进行实验。

3.2 性能评价指标

在不平衡数据中,少数类通常代表领域的本质,错误预测少数类样本的代价往往高于错误预测大数类样本的代价,因此,传统的预测精度并不适合作为不平衡数据学习性能的评价指标。本文采用文献[23]的建议,使用MG[24]和MAUC[25]作为算法性能的评价指标。MG和MAUC的定义分别如下:

(12)

(13)

MG强调各类预测精度之间的平衡。假设算法在大数类上有较高的预测精度,在少数类上有较低的预测精度,最终会产生低MG值。MAUC是所有类进行成对比较形成的AUC值的平均,其不依赖于具体的决策阈值,是对算法综合性能的最常用评价。此外,MG和MAUC作为不平衡学习领域广泛使用的评价指标,一个显著的优点是它们同时适应于二分类和多分类不平衡数据,且具有统一的表达形式。

3.3 实验数据

为了得到一个可靠的性能评价,从UCI数据库中选择16个类不平衡的数据集,该数据集具有不同的样本大小、特征维度和类别数目,其中较高维(高于100维)的数据集为8个。按特征维度为100将这16个数据集划分为2组,一组为特征维度低于100的普通数据集,另一组为特征维度高于100的高维数据集。表1总结了该2组数据集的特征。

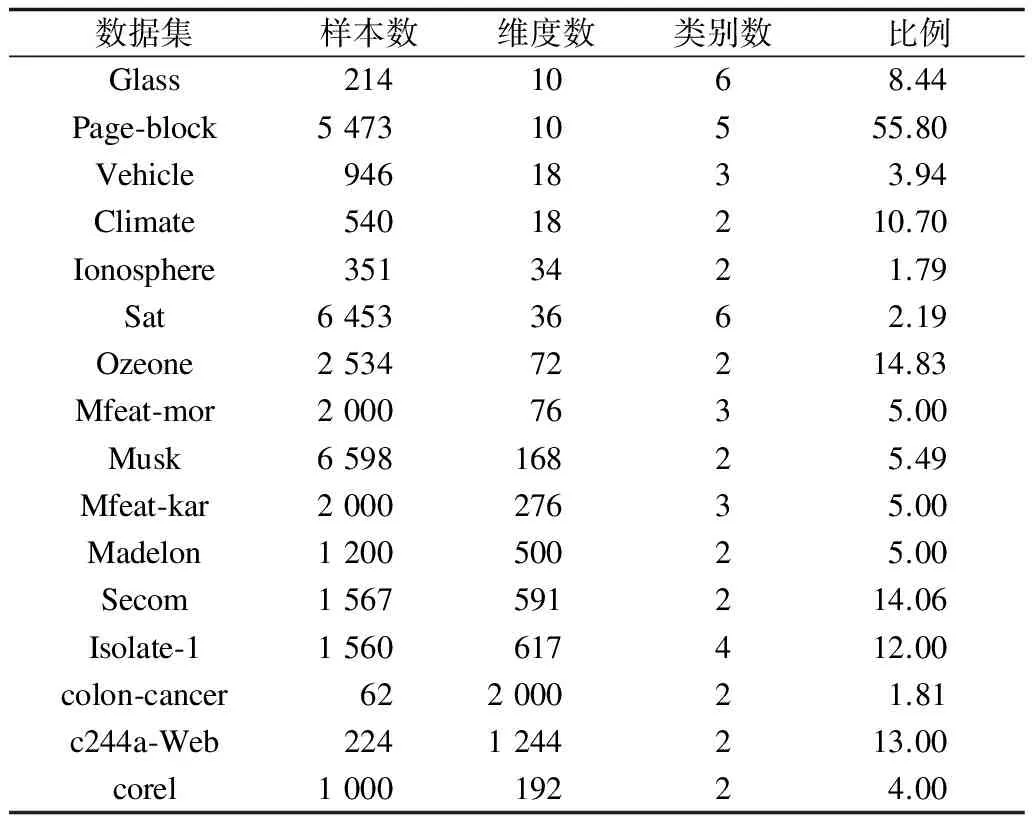
表1 数据集基本信息

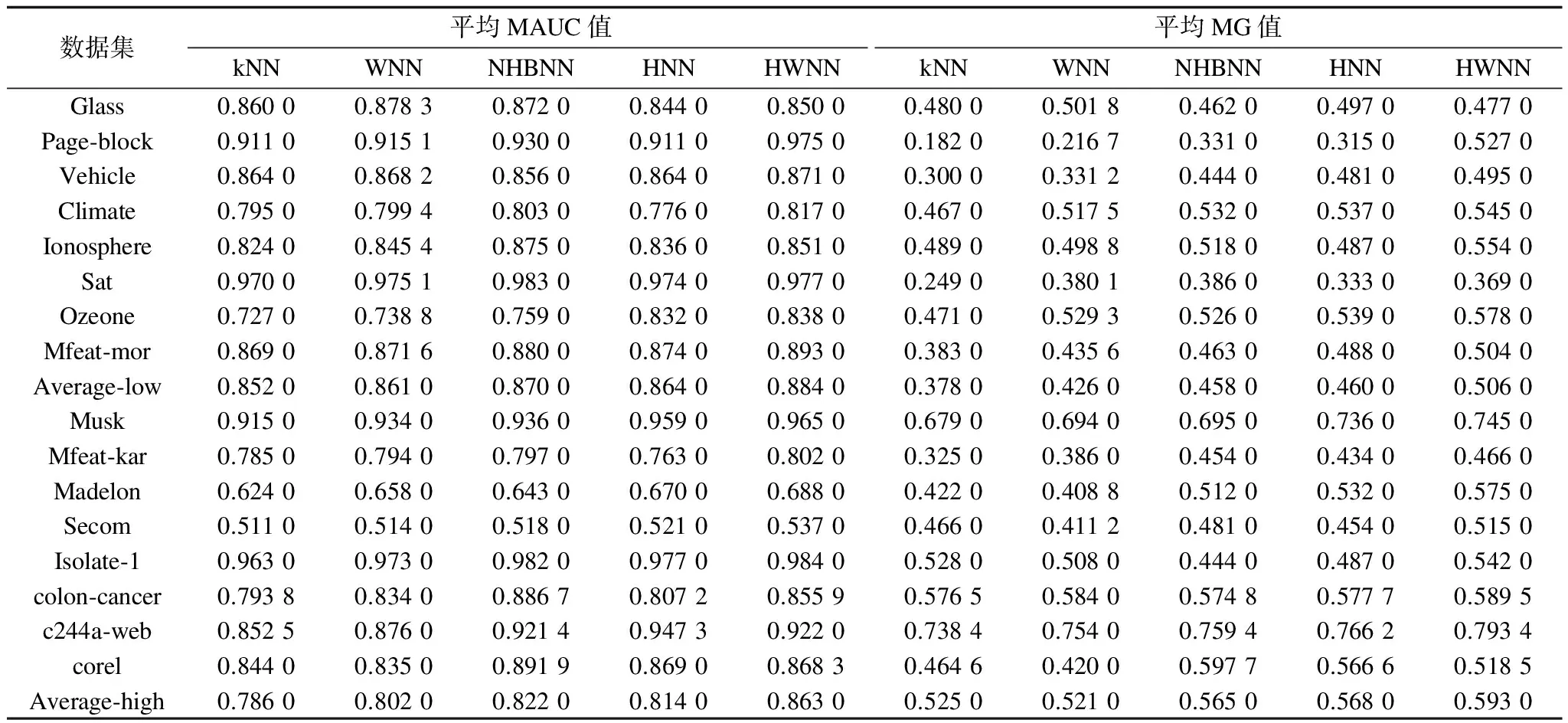
不平衡度IR用于衡量数据集的类不平衡程度。假设类依据样本大小以降序排序,即如果i

(14)

从式(14)可以看出,对于一个类分布平衡的数据集,其相应的IR为0。IR越高表示类分布越不平衡。

3.4 结果分析

为了使实验结果更具客观性,采用10折交叉验证的方法,利用5种分类算法对训练集中的数据进行分类学习,并用测试集进行测试,10次测试结果的平均值作为1次10折交叉验证的结果,实验数据如表2所示。其中,Average-low与Average-high分别为该算法在8个低维数据集和8个高维数据集上的平均MAUC值和平均MG值。

表2 不同分类算法的MAUC值和MG值

从表2中可以看出,在低维数据集上,本文HWNN算法的平均MAUC值和MG值均高于其他分类算法,这是因为HWNN算法引入了类加权因子,纠正了向大数类倾斜的现象,而其他算法忽略了不平衡因素对分类结果的影响,导致性能较差。此外,在高维数据集上,各分类算法的分类精度均有所下降,这是由高维数据特性所导致,但是本文HWNN算法仍能达到较高的平均MAUC值和平均MG值。相对于低维数据分类情况,HWNN算法在高维数据上分类精度的优势更明显和突出,证明了该算法对高维不平衡数据具有较强的适应性。

4 结束语

针对高维不平衡类数据的学习,本文提出一种基于Hubness和类加权的kNN分类算法HWNN。用样本的k发生分布来缓解高维数据空间中产生的hubs对kNN分类的损害,通过使用类加权的方式提高少数类在样本k发生中的比例以改进其对少数类的预测精度。在16个UCI标准数据集上的实验结果表明,无论是普通维数据还是高维数据,相较于已有的几种基于Hubness的kNN算法,HWNN算法具有较高的性能。由于HWNN算法采用的类加权是采用全局的方式对各类的权重进行赋值,因此,下一步将考虑测试样本所在的局部环境,使算法更适应高维不平衡分类的特异性偏置。

[2] BISHOP C M.Pattern recognition and machine learning[M].Berlin,Germany:Springer,2006:461-462.

[3] HASTIE T,TIBSHIRANI R,FRIEDMAN J.The elements of statistical learning:data mining,inference and predic-tion[J].The Mathematical Intelligencer,2005,27(2):83-85.

[4] WEISS G M.Mining with rarity:a unifying frame-work[J].ACM SIGKDD Explorations Newsletter,2004,6(1):7-19.

[5] CHAWLA N V,JAPKOWICZ N,KOTCZ A.Editorial:special issue on learning from imbalanced data sets[J].ACM SIGKDD Explorations Newsletter,2004,6(1):1-6.

[6] LIN W J,CHEN J J.Class-imbalanced classifiers for high-dimensional data[J].Briefings in Bioinformatics,2013,14(1):13-26.

[7] YIN H,GAI K.An empirical study on preprocessing high-dimensional class-imbalanced data for classification[C]//Proceedings of International Conference on High Performance Computing and Communications.Washington D.C.,USA:IEEE Computer Society,2015:1314-1319.

[8] DIETTERICH T,KEARNS M,MANSOUR Y.Applying the weak learning framework to understand and improve C 4.5[EB/OL].[2017-03-02].http://www.doc88.com/p-9864143758186.html.

[9] CIESLAK D A,CHAWLA N V.Learning decision trees for unbalanced data[C]//Proceedings of European Conference on Machine Learning and Knowledge Disco-very in Databases.Berlin,Germany:Springer,2008:241-256.

[10] QUINLAN J R.Improved estimates for the accuracy of small disjuncts[J].Machine Learning,1991,6(1):93-98.

[11] LIN Y,LEE Y,WAHBA G.Support vector machines for classification in nonstandard situations[J].Machine Learning,2002,46(1):191-202.

[12] WU G,CHANG E Y.KBA:kernel boundary alignment considering imbalanced data distribution[J].IEEE Transactions on Knowledge and Data Engineering,2005,17(6):786-795.

[13] ZHANG X,LI Y.A positive-based nearest neighbour algorithm for imbalanced classification[M]//PEI J,TSENG V S,CAO L B,et al.Advances in Knowledge Discovery and Data Mining.Berlin,Germany:Springer,2013:293-304.

[14] LI Y,ZHANG X.Improving k nearest neighbor with exemplar generalization for imbalanced classification[C]//Proceedings of Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining.Berlin,Germany:Springer,2011:321-332.

[15] TAN S.Neighbor-weighted k-nearest neighbor for unbalanced text corpus[J].Expert Systems with Applications,2005,28(4):667-671.

[16] DUBEY H,PUDI V.Class based weighted k-nearest neighbor over imbalance dataset[M]//PEI J,TSENG V S,CAO L B,et al.Advances in Knowledge Discovery and Data Mining.Berlin,Germany:Springer,2013:305-316.

[20] 翟婷婷,何振峰.基于Hubness的类别均衡的时间序列实例选择算法[J].计算机应用,2012,32(11):3034-3037.

[21] 张巧达,何振峰.基于Hub的高维数据初始聚类中心的选择策略[J].计算机系统应用,2015,24(4):171-175.

[22] ZUO W,ZHANG D,WANG K.On kernel difference-weighted k-nearest neighbor classification[J].Pattern Analysis and Applications,2008,11(3):247-257.

[23] WANG S,YAO X.Multiclass imbalance problems:analysis and potential solutions[J].IEEE Transactions on Systems Manand Cybernetics,Part B,2012,42(4):1119-1130.

[24] SUN Y,KAMEL M S,WANG Y.Boosting for learning multiple classes with imbalanced class distribution[C]//Proceedings of International Conference on Data Mining.Washington D.C.,USA:IEEE Computer Society,2006:592-602.

[25] HAND D J,TILL R J.A simple generalisation of the area under the ROC curve for multiple class classification problems[J].Machine Learning,2001,45(2):171-186.