基于显著性与弱凸性的三维点云模型分割

,

(中北大学 计算机与控制工程学院,太原 030051)

0 概述

近年来,随着计算机图形学、三维扫描设备技术的发展以及计算机硬件技术的提高,三维模型不仅在数量上有了飞跃性的增长,而且其应用越来越广泛,应用领域涉及工业产品设计、虚拟现实、三维游戏、建筑物设计、影视动画、医学诊断和分子生物研究等方面。基于三维模型的几何处理成为近年来计算机辅助设计和图形学研究的热点。但由于原始的三维点云模型缺乏足够的结构特征和语义信息,因此难以对其进行有效分割。

目前关于三维模型分割的研究较多。其中:文献[1]对三维模型进行近似凸分解,通过贪心算法识别三维模型的凹区域,将其递归地分解成更凸的组件;文献[2]提出一种通过贪心区域增长获得弱凸组件的方法。这2种方法需要将三维点云模型转化为网格模型,同时考虑形状的体积。文献[3]提出一种基于显著性的迭代分割方法,通过突出程度、特征选择和高斯映射将三维模型分割为小于阈值的组件。文献[4]提出由测地距离的积分定义的连续函数检测突出程度的方法。文献[5]提出通过凹权重定义2个邻接面间的距离,利用随机游走方法把每个面分配给对应的种子点实现网格过分割,最终通过基于加权的公共边界长度迭代合并相邻部分。文献[6-7]提出基于凹凸性和曲率的特征点确定方法。文献[8]基于空间邻域提出一种改进的模糊C均值算法。文献[9]由过分割产生的块之间几何关系和凹权重构建关联矩阵,通过本征间隙标准确定分割数量,由节点集和节点域理论确定分割边界进行三维模型的分割。文献[10]提出一种计算封闭二维流形边界上点云SDF值的方法,基于SDF值将三维模型分割成厚度相同的组件。文献[11-12]提出基于体素特征的分割方法。文献[11]首先将三维点云模型过分割为超体素,然后通过法向量夹角确定超体素之间的凹凸性,最后引入一种局部受限、有向的加权一致性算法确定切割平面。文献[13-14]提出由凹凸信号确定凹特征点,然后通过区域中心线提取算法以及扇形探射线算法构造闭合分割线的方法。

为进一步优化三维点云模型的分割效果,本文提出一种基于弱凸性和显著性的分割方法。首先利用相互可见性,通过谱聚类算法将模型过分割为弱凸块;然后通过边界强度和突出定义显著性,选取有意义的弱凸块;最后基于相互可见性和体积相似性对弱凸块进行合并,得到有效的组件,并对最终结果进行评价。

1 基于显著性和弱凸性的分割方法

如图1所示,本文方法主要包括以下步骤:首先通过计算三维点云模型的法向量间夹角构建关联矩阵,利用谱聚类方法将点云过分割为弱凸块(如图1(b)所示);然后通过显著性测试提取较小的突出部分和面积较小但边缘特征点明显的弱凸块,对其他弱凸块则利用Asafi定义的相互可见性[15]属性合并为弱凸组件(如图1(c)所示);最后根据SDF[16]定义体积相似性,合并弱凸组件和显著性判定时提取的弱凸块(如图1(d)所示)。

图1 本文方法各步骤示意图

2 弱凸分解

弱凸分解与三维模型分割具有紧密关系。这2个问题都与“最小规则”有关,其对三维点云模型分割以最小曲率线划分,这意味着一个“子部分”可被看作是由近似凸的部分组成。本文通过谱聚类将三维点云模型过分割为弱凸块,具体过程如下:

1)构建关联矩阵Wn×n(n为点云的数量),确定初始聚类数目为K,当点i与点j互为k近邻点且两点之间凹凸性判定为凸时,Wi,j=1,其他情况下为0。

2)计算对角矩阵Dn×n,对角线上的值为Wn×n矩阵中对应行的和。

3)计算拉普拉斯矩阵L=D-W并进行归一化处理。

4)求解L的3K个特征值,按降序排序,并计算它们的均值λ,获取其索引值i。选取特征值的区间为A=[i-(K+1)/2,i+(K-1)/2],同时求解对应于特征值的特征向量。

5)利用K-means++聚类算法将三维点云模型聚为K类,输出K个弱凸块P={P1,P2,…,PK}。

3 显著性判定

三维点云模型通过弱凸分解产生的部分弱凸块已经具有意义,为防止其在后续相互可见性算法中被合并,检测这些弱凸块,并将其标记为S={S1,S2,…,St}。本节提出一种“视觉突出判定分割结果”的方案,其基于认知心理学中的“部分显著性”理论。该理论认为“子部分”的显著性通常由3个因素决定:边界强度,突出,相对尺寸。本节通过突出和边界强度判定显著性,首先给出定量定义,然后描述它们在分割过程中的具体计算方法。

1)边界强度:根据横截性原理,组件边界通常位于凹陷处。文献[17]指出,边界强度由法线转向决定,如图2所示,对于二维轮廓,分割边界的两侧通常具有2条法线,并且它们之间的角度可以在某种意义上表示该边界的强度。对于三维形状,高斯曲率可用于测量组件边界的强度。

图2 法线变化决定边界强度示意图

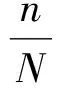
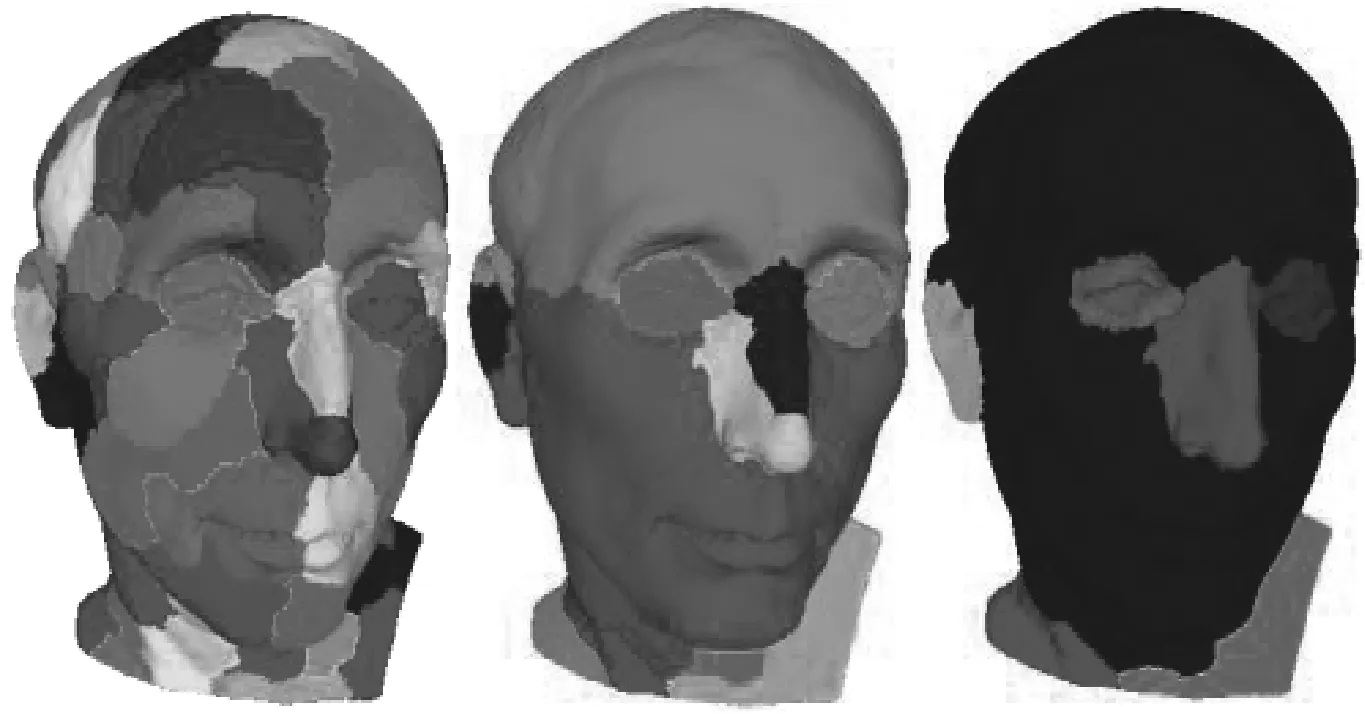
图3 边界特征点选择示例(人的眼睛)

2)突出:此因素描述组件从其主体突出的程度。对于二维模型轮廓,可以量化为组件的周长(不包括其底部)与其底部长度的比率。对于3D形状,组件的底部为组件的边界形成的表面。因此,三维模型组件的突起可以被量化为组件表面的面积与其底面的面积的比率或组件上点到底面的最大距离与底面最大拟合圆的半径的比率。

通过弱凸块轮廓上的点拟合平面检测突出性。本文通过有向的加权一致性算法拟合平面,并通过S上点到拟合平面的最大距离判断其突出性。典型的RANSAC算法可以平等地处理点云,根据“部分显著性”理论,组件边界通常位于凹陷处,为边界点赋予权值,将凹点赋值为1,凸点赋值为0,将其扩展为加权的RANSAC算法。利用加权的RANSAC算法使拟合平面包含具有高权值的点,排除低权值的点。平面模型的得分通过下式得出:

(1)

其中,P为具有高权值点的集合,ωi为边界点的高斯曲率。

令S为弱凸块,计算S上点到拟合平面的最大距离d,并令r为拟合平面上最大包围圆的半径。如果d/r>ε2,则接受此弱凸块,ε2=0.74。上述过程示例如图4所示。

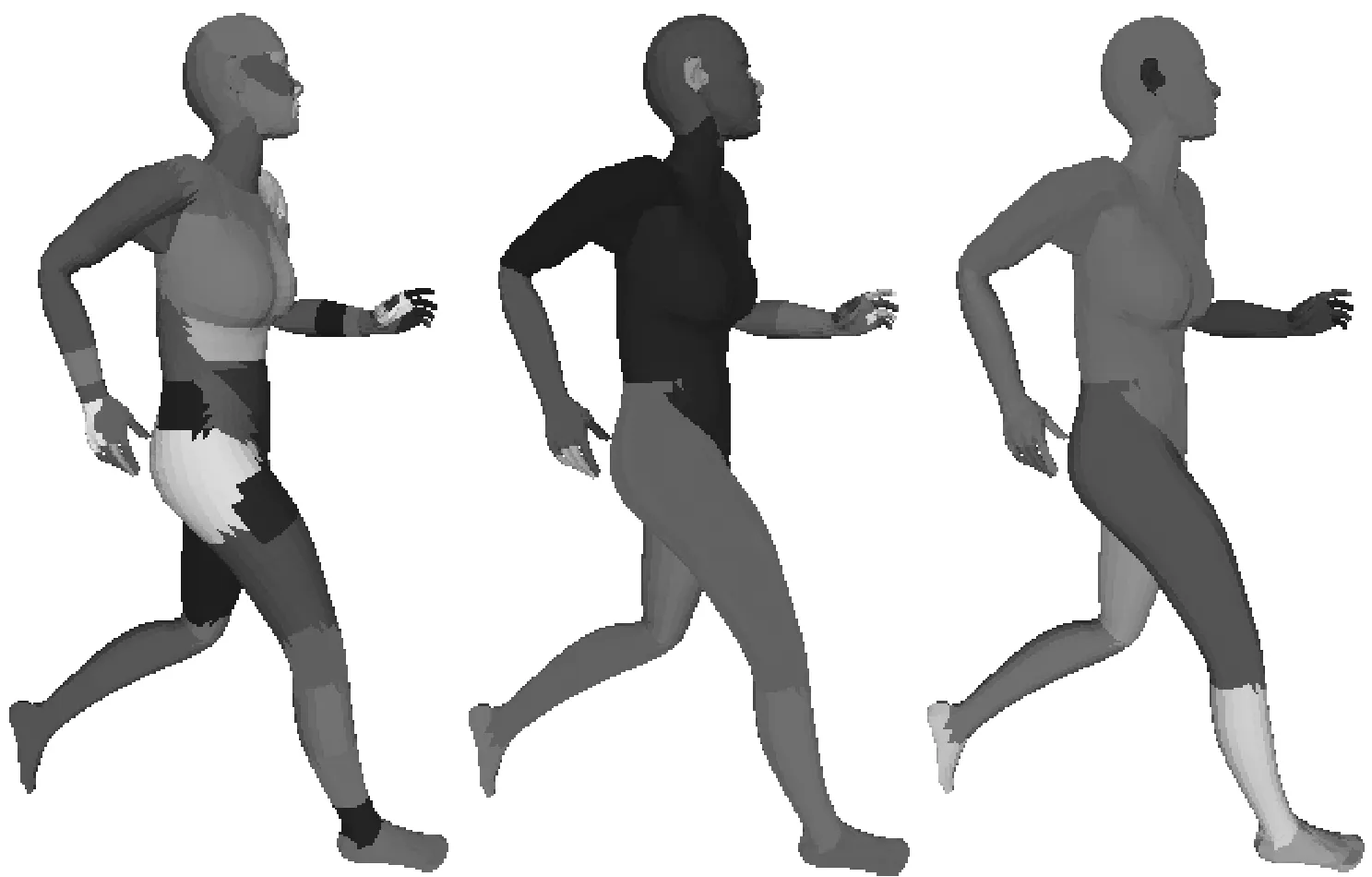
图4 突出性选择示例(人的耳朵)

通过显著性判定可以选择较小的突出部分和面积较小但边缘特征点明显的分割部分,防止其在后续的相互可见性合并算法中被合并。

4 区域合并

本节提出区域合并算法,首先给出相关定义。

定义1(相互可见性) 令S为弱凸块上的随机采样点的集合,LLoS(S)为S中相互可见点的对数的集合。对于2个弱凸块上的取样点子集A、B包含于S,LLoS(A,B)为(i,j)的集合,其中i∈A,j∈B,且i、j是相互可见的。S的凸度等级定义为:

(2)

其中,|LLoS(S)|为S中可见对的数量,|S|为取样点的数量。相互可见性定义示意图如图5所示,其中实线表示两点可见,点划线为不可见。

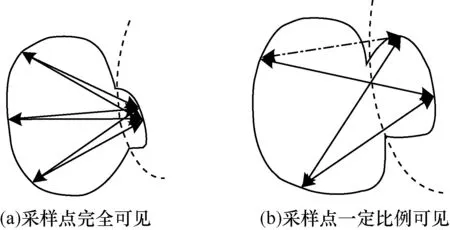
图5 相互可见性定义示意图

定义2(体积相似性) 给定2个相邻的弱凸组件Ci和Cj,通过文献[16]提出的形状直径函数计算其直方图,然后利用EMD距离计算2个相邻弱凸组件之间的相似性,具有高体积相似性的2个相邻弱凸组件可能属于相同的语义形状部分,可以被合并。

ddist(Ci,Cj)=EEMD(hi,hj)

(3)

4.1 相互可见性合并

根据弱凸块的相互可见性将弱凸块聚类成较大的弱凸组件。目标是最小化所得到的组件的数量,同时保持组件内相互可见性高于阈值θ。该阈值量化了允许合并的弱凸块偏离完美凸度的程度。本文采用迭代合并方法,其中第1次迭代严格执行弱凸块之间的相互可见性,以下迭代逐渐放宽此约束。每次迭代根据弱凸块的相互可见性以贪婪的方式合并多对相邻的弱凸块。

给定一组初始的弱凸块P={P1,P2,…,Pn-t},根据相邻块之间的相互可见性合并获得一组弱凸组件C={C1,C2,…,Cm},每个组件Ci对应于弱凸块Pi。执行合并迭代首先通过弱凸块的相互可见性按照降序对所有相邻组件对进行排序;然后按照这个顺序,对满足于θ的Ci和Cj的所有成对组合进行合并。这种迭代方法的优点在于:允许在早期的迭代中创建高度自我可见的组件,如果它们的更新的相互可见性允许,将进一步扩展并与其他组件融合。本文采用3次迭代:θ1=0.9,θ2=0.8,θ3=0.7。

4.2 体积相似性合并

在一些情况下,通过上述步骤形成的弱凸组件已经具有意义。然而,对于结构复杂的三维模型需要进一步对组件合并以达到接近语义的分割,在如图6所示的手模型中,根据显著性提取的中指上端部分,需要根据体积相似性进行进一步合并,相似性由基于形状直径函数的分量特征决定。

图6 相似性合并示意图

体积相似性合并过程如下:

1)给定一组弱凸组件C={C1,C2,…,Cn}={C1,C2,…,Cm,S1,S2,…,St},对于每个组件Ci,通过计算SDF值的直方图确定体积特征。首先在每个Ci的表面上均匀采样s个点,每个采样点Pμ∈Ci形成具有角度α的锥体的尖端,方向为-n,其中nμ是Pμ的法线;然后计算落在圆锥体内的射线段,利用Pμ的法线和射线之间的夹角的余弦加权这些射线段;最后选择中位数作为该点的SDF值。当没有这样的射线落在该点的锥体内时,该点被标记为平面。本文实验中使用参数α=2π/18。

2)使用所有Pμ∈Ci的SDF值,创建一个直方图,获取Ci的体积分布。当Ci为平面或近似平面的情况下,Ci中的绝大多数点将被标记为没有SDF值,由此产生的hi将被错误地判定为空,因此,将判定为空的组件标记为平面。然后将平面组件从下一个合并步骤中排除,并在稍后处理。

3)使用体积特征,根据式(2)计算所有成对弱凸组件之间的相似性,构建距离矩阵D,同时考虑一对弱凸组件之间的接缝的凸度,用于选择哪个相邻组件是合并的最佳选择。对于弱凸组件,利用k-nearest图和边界长度加权定义组件边界的凸度:

(4)

(5)

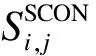
5 实验结果

在Windows系统上,以普林斯顿数据集为基准,通过文献[18]提供的软件进行评估、分析,为完整起见,本文同时增加COSEG数据集[19]和文献[20]的数据集,实验环境为Intel Core i3 3.3 GHz CPU,4 GB内存。

本节评估并比较本文方法和Heterogeneous[9]、SDF[10]、Constraint Planar[11]、Convex-Concave[12]4种方法,评价指标为Rand指数、Hamming距离、分割差异性、全局与局部一致性误差。其中:Rand 指数通过分析一对点在实际分割和基准分割中是否处于相同分割部分建立对模型分割结果的评价;Hamming 距离通过计算分割部分之间的汉明距离来定量计算整体区域差异;分割差异性通过计算边界距离度量分割差异,具体通过计算实际分割边界中的点与基准分割边界中最近点的距离的和得到;全局与局部一致性差异用来测量分割结果层次的相似性和差异,全局一致性差异要求所有分割结果的细化方向相同,局部一致性差异则允许分割结果在不同方向细化。图7显示了上述4项指标的比较结果,图8显示了数据集中代表性模型的分割效果。实验结果表明,本文提出的方法优于无监督方法,可以同时分割大的分支(胳膊、头部)和小的细节部分(眼睛、指头),提高了分割结果层次的相似性,同时对局部的表面扰动和非刚性变化的鲁棒性较好。

图7 分割评估结果

图8 本文算法在3种数据集上的分割效果

6 结束语

本文基于显著性和弱凸性提出一种新的三维点云模型分割方法。通过显著性判定提取部分有意义的“子部分”,利用显著性解决欠分割问题,通过相互可见性和体积相似性解决过分割问题,最终得到有效的分割结果。实验结果表明,本文方法能够有效提高分割质量,但其不足之处是对于点云密度较小的模型得到的分割边界质量较差,需要通过重采样获取较好的结果。此外,其对于鱼类等平滑模型缺乏清晰的几何边缘,分割效果也欠佳,下一步将针对上述问题对本文方法进行改进。

[1] LIEN J M,AMATO N M.Approximate convex decomposi-tion of polyhedra and its applications[J].Computer Aided Geometric Design,2008,25(7):503-522.

[2] KREAVOY V,DAN J,SHEFFER A,et al.Model composition from interchangeable components[C]//Proceedings of the 15th Pacific Conference on Computer Graphicsand Applications.Washington D.C.,USA:IEEE Press,2007:129-138.

[3] CHEN H K,HE Y D.A novel part-salience-based approach to fast iterative 3D mesh segmentation[C]//Proceedings of International Symposium on Computer.Washington D.C.,USA:IEEE Press,2016:311-314.

[4] AGATHOS A,PRATIKAKIS I,PERANTONIS S,et al.Protrusion oriented 3D mesh segmentation[J].Visual Computer,2010,26(1):63-81.

[5] LAI Y K,HU S M,MARTIN R R,et al.Rapid and effective segmentation of 3D models using random walks[J].Computer Aided Geometric Design,2009,26(6):665-679.

[6] 史皓良,吴禄慎,余喆琦,等.散乱点云数据特征信息提取算法[J].计算机工程,2017,43(8):279-283.

[7] 朱世松,樊菁芳,朱洪锦.基于轮廓特征点的重叠车辆检测与分割[J].计算机工程,2016,42(7):244-250.

[8] 王禹君,周菊香,徐天伟.改进模糊C均值算法在民族服饰图像分割中的应用[J].计算机工程,2017,43(5):261-267.

[9] THEOLOGOU P,PRATIKAKIS I,THEOHARIS T.Unsupervised spectral mesh segmentation driven by heterogeneous graphs[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2017,39(2):397-410.

[10] HUSKA M,MORIGI S.A meshless strategy for shape diameter analysis[J].Visual Computer,2017,33(3):303-315.

[11] SCHOELER M,PAPON J,WORGOTTER F.Constrained planar cuts-object partitioning for point clouds[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Press,2015:5207-5212.

[12] 马元魁,白晓亮.三角网格模型体素特征分割[J].计算机科学,2015,42(10):13-15.

[13] 王泽昊,黄常标,林忠威.三角网格模型的最小值边界分割[J].计算机辅助设计与图形学学报,2017,29(1):62-71.

[14] 董洪伟,李 重,周儒荣,等.基于凹凸信号的网格分割[J].计算机辅助设计与图形学学报,2009,21(3):295-304.

[15] ASAFI S,GOREN A,COHEN-OR D.Weak convex decomposition by lines-of-sight[J].Computer Graphics Forum,2013,32(5):23-31.

[16] SHAPIRA L,SHAMIR A,COHEN-OR D.Consistent mesh partitioning and skeletonisation using the shape diameter function[J].Visual Computer,2008,24(4):249-259.

[17] HOFFMAN D D,SINGH M.Salience of visual parts[J].Cognition,1997,63(1):29-78.

[18] CHEN X,GOLOVINSKIY A,FUNKHOUSER T.A benchmark for 3D mesh segmentation[J].ACM Transactions on Graphics,2009,28(3):341-352.

[19] WANG Y,ASAFI S,KAICK O V,et al.Active co-analysis of a set of shapes[J].ACM Transactions on Graphics,2012,31(6):165.

[20] BENHABILES H,VANDEBORRE J P,LAVOUE G,et al.A framework for the objective evaluation of segmentation algorithms using a ground-truth of human segmented models[C]//Proceedings of IEEE International Conference on Shape Modeling and Applications.Washington D.C.,USA:IEEE Press,2009:36-43.