水下航行器壳体结构参数对隔振的影响
(渤海船舶职业学院 动力工程系,辽宁葫芦岛 125105)
0 引言
目前,水下航行器在军事与民用领域均得到了广泛应用,并不断向高性能、轻型化发展。水下航行器壳体主要用于承受外部水压、保持水密和作为内部设备的支撑,航行器各个系统中的装置和元件通过安装结构或联接结构安装在壳体上。在航行过程中,动力系统产生的机械振动会通过连接结构传递到壳体上,壳体受到激励作用产生振动。壳体振动一方面直接产生噪声辐射出去,经研究表明,在5 kHz以下频段,壳体振动的辐射噪声能占总辐射能量的80%~90%[1];另一方面,振动通过壳体进行传递,产生自噪声,并对其他系统造成影响。由此可知,水下航行器的壳体辐射噪声为其主要辐射噪声之一,而影响壳体辐射噪声的主要因素是刚度和固有频率,刚度和固有频率又取决于壳体结构各参数,包括壳体壁厚、筋板个数、筋板宽度和筋板厚度。为此,本文利用波动法分析水下航行器壳体各参数对壳体频率的影响,旨在减小振动向壳体的传递、提高隔振效果,从而为水下航行器壳体结构优化设计和制造提供依据。
1 波动分析法计算壳体固有频率的原理
由于水下航行器的壳体辐射噪声为其主要辐射噪声之一,因此壳体的刚度和固有频率也成为降低水下航行器壳体辐射噪声的关键。使用波动法研究壳体结构各参数,分析其对壳体的刚度和固有频率的影响。
水下航行器壳体固有频率在理论上通常采用波动法计算。首先建立和分析水下航行器的壳体数学模型(连续系统),然后依据波动方程[2]和胡克定律求出壳体的变形能和动能,最后根据瑞利法的原理计算出固有频率。
1.1 波动方程
在建立水下航行器壳体的数学模型时,将壳体的两端进行简支处理,如图 1所示。根据波动方法可知壳体的位移表达式的边界条件为:在壳体两端,径向和切向位移为零、弯矩为零,即m=n=0;Mx=0(x=0,L)。
根据边界条件,假设位移为
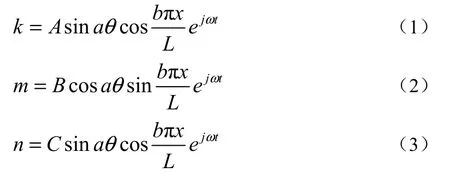
式中:a为纵向半波数;b为周向整波数;ω为圆频率;A、B、C分别代表三个方向的波速。

图1 壳体结构示意图
1.2 壳体的变形能和动能
水下航行器壳体主要由肋骨和壳板两部分组成,壳体的最大动能和最小势能均由肋骨和壳板两部分组成[3]。弹性体的最大应变能表达式为

根据直线法假定可知σz=γyz=γzx=0,dy=Rdθ,由胡克定理可知
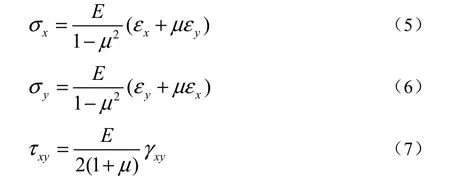
由材料力学可知,壳体的势能(变形能)由轴向和周向的拉压应变和剪切应变组成。
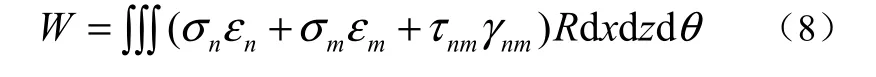

式中:nε′、mε′分别为圆柱壳体中面的轴向和周向的变化;γn′m为圆柱壳体中面扭转变化;H为壳体中面到圆柱壳体中心的距离。

代入势能公式可求出壳体的变形能为(令t=0)

壳体肋板的变形由压缩变形和弯曲变形组成,并以弯曲变形为主,因而压缩变形能忽略不计。因此,壳体肋板变形能为
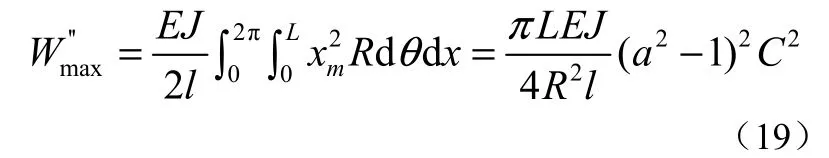
因此,总的变形能为

与变形能一样,壳体的动能也由两部分组成。壳板的动能为

肋板的动能为

总动能为

1.3 壳体频率
根据瑞利法可知F=Wmax-Tmax=E,可得F的三个方向的偏导为零。

由此得到一个三维的线性方程组,因为A、B、C不可能同时为零,根据线性代数理论,可以求出固有频率。由经验确定最小频率为径向频率。
1.4 各参数变化对系统固有频率的影响计算分析
选取不同的壳体壁厚、筋板个数、筋板宽度和筋板厚度,进行程序计算。通过计算得出程序计算结果图,如图2所示。从图2可以看出:增加筋板的厚度可以明显提高壳体的固有频率;增加壳体的壁厚,壳体的固有频率略有下降;增加筋板的个数和宽度也有助于提高壳体的刚度。壳体的固有频率是随着其刚度的增加而增加的,依据这个规律,确定通过增加筋板的厚度来加大壳体的固有频率并保证对壳体质量的影响最小的研究方案。

图2 程序计算结果图
2 有限元分析壳体刚度对系统振动传递的影响
2.1 试验验证
为验证有限元计算的正确性,针对有筏体、无油方案的舱段建立有限元模型,建模时按实体进行 1:1建模,计算时采用和试验相同的材料,采用四面体单元进行网格划分。水下航行器舱段固有频率有限元计算结果与试验结果如表1所示。

表1 水下航行器舱段固有频率
从表 1可以看出:有限元计算得出的第一阶、第二阶、第六阶、第七阶固有频率与通过试验测得的结果基本相同,说明有限元模型的建立和边界条件的设定是合理的,计算可靠。
2.2 壳体刚度对隔振的影响
采用前面建立的有限元模型,用三种材料来研究壳体刚度对振动传递的影响。在保证壳体质量不变的情况下,选用了三种弹性模量不同的材料,材料 1的弹性模量是材料2的10倍,材料3的弹性模量是材料2的1/10倍。在有限元计算中,将单位简谐力作为激振力,计算的频率设定为0~1 500 Hz。通过设定相同的材料密度和三种不同的弹性模量,使用有限元分析软件计算,得出三种情况下的壳体位移响应曲线,如图3所示。由图3可以看出:频率在250 Hz以下时,三种材料的位移曲线基本重合;频率在250 Hz~950 Hz之间时,材料1和材料2的位移响应曲线基本重合,材料 3的响应曲线的变化较大(时而明显降低,时而明显增加);频率在950 Hz以上时,三种材料的位移相应曲线又基本重合。

图3 不同壳体刚度在单位力激励下的位移响应曲线
由以上分析可知:不能简单地从壳体的刚度大小来判断水下航行器动力舱段的振动传递的好坏,应该要根据整个系统的动态特性(包括浮筏系统的质量比和刚度比、减振器的动态特性等)来分析。加大壳体的刚度能够提高壳体的固有频率,并减小系统在低频的振动偶合。
3 隔振器刚度对振动传递的影响
取某舱段动力设备的浮筏隔振器的不同刚度,即设定橡胶材料的弹性模量E2=5.68×106N/m2,再取E1=0.1E2、E3=10E2分别加以计算,比较隔振器刚度对其固有频率的影响,如图4所示。

图4 固有频率曲线对比图
通过图 4可以看到:隔振器刚度对系统固有频率的影响很大。随着隔振器刚度的增加,系统的固有频率也随着增加,这与振动理论相符合。从这个系统的模态变形看,前 7阶都是隔振器变形,其他部分呈刚体运动状态,因此可通过降低隔振器的刚度来降低系统的固有频率,起到好的隔振效果。
4 结论
通过计算壳体频率并分析其刚度对振动传递的影响,可知加大筋板的厚度可以在保证壳体重量增加最小的前提下提高水下航行器的壳体刚度,进而提高系统的固有频率,减小振动向壳体的传递,达到提高隔振效果的目的。
参考文献:
[1] 贾锐. 水下航行器壳体结构动态设计方法研究[D].西安: 西北工业大学, 2007.
[2] 左言言. 壳体结构受激振动传播特性的研究——用频率-波数分析法研究结构振动的探索[D]. 江苏镇江: 江苏理工大学, 1996.
[3] 许建. 用能量法计算环肋柱舱段的固有频率[J].船舶工程研究, 1998(1): 33-41.

