人人都能学会编程

伍先军

2017年7月，国务院印发了《新一代人工智能发展规划》，明确要求“实施全民智能教育项目，在中小学阶段设置人工智能相关课程，逐步推广编程教育，鼓励社会力量参与寓教于乐的编程教学软件、游戏的开发和推广”，使中小学普及编程教育上升为国家战略。对人工智能和编程的理解，许多人认为人工智能属于更高级的范畴，编程只是其中的一部分，其核心在于算法，所以在中小学编程教学过程中应更注重算法教育，这样才能更好地过渡到人工智能的学习。

传统编程教学的困境

传统的编程教学是在上世纪70年代末80年代初起步，到本世纪初，教材基本就是某种计算机高级语言的操作说明书，教师和学生都以软件操作为核心，课堂几乎成为公司软件培训部，这种教学模式可称为“程序教学1.0”。这种以程序设计语言语法为中心、按成人短训班模式组织教学的做法，可能适合有大块自由时间消化、肯主动钻研的大学生，但不适合课时极少、几乎无自由时间可支配、自我约束能力较弱的中小学生。

2003年启动的信息技术课程改革，在“程序设计”前面增加了“算法”，教学以“解决问题”为目的。但在教学实践中暴露出诸多问题：一是“算法”与“程序设计”常常脱节——先讲算法，容易纸上谈兵，空洞说教，或者讲清楚了算法，却没时间编程实现；先讲程序设计，算法就显得多余甚至是累赘。二是“程序设计”本来概念就多而且难懂，如常量、变量（数组）、数据类型、运算符、表达式（算术表达式、关系表达式、逻辑表达式、字符串表达式等）、函数（内置函数、自定义函数）、过程，还有各种语句（如输入、输出、赋值、条件、循环语句）的语法。若采用面向对象的程序设计，还有各种控件（类）、对象、属性、方法、事件等高难度概念。现在引入“算法”后，又新增了许多内容，以及一些常见算法，如解析法、迭代法、穷举法、二分查找、排序算法、遞归算法等。三是由于课时少，上机时间不足，学生编写代码、调试程序经常出错，往往无法得到及时解决，难以形成知识积累和意义建构，致使每节课几乎都是零起点，久而久之，学生对程序设计容易产生恐惧甚至厌恶心理。这种教学模式，可称为“程序教学2.0”，虽然引入了“算法”，但没有厘清“算法”与“程序设计”的关系、面向过程程序设计与面向对象程序设计的关系，导致“头发胡子一把抓”，不但原来“程序设计”的问题没有解决，还增加了新的矛盾。

这一轮课改也在高中数学中引入了“算法”，出现在必修3第一章“算法初步”中。然而，放眼高中数学算法教学课堂，我们会发现“纸上谈兵”几乎是普遍现象。一是许多数学教师的算法水平和实现能力偏低，只会“纸上谈兵”。算法是高中数学新课程新增内容，许多一线高中数学教师，尤其是年龄较大的教师，求学期间没有系统地学习过算法，在职业培训时也没有及时有效地跟进，他们缺乏在计算机上验证程序的意识和能力，一般只会“纸上谈兵”式地模拟计算机执行流程图，几乎不安排学生集体上机实践，从而将本来实践性强、生动有趣的内容变成了机械呆板、枯燥乏味的说教。二是“固化”“机械”的高考题型助长了教师的“纸上谈兵”。由于多数高考题似乎就只考“根据流程图写出程序运行结果”这种题型，而且往往只需照着框图模拟运行几趟（一般是3～6趟）就能直接得到结果，这种极端机械的题型，使得大部分一线数学教师和学生坚信只需“纸上谈兵”即可，从而大大削弱了算法教学。三是算法教学存在两大“结构性”障碍，让师生止步于“纸上谈兵”：①分析问题时，在得出了用自然语言表示的解题步骤之后，怎么把它转化为流程图呢？无论是在纸上还是在黑板或电子白板上画，无论用纸笔还是用Word、Visio等软件画流程图，都费时费力。②好不容易画出流程图后，再怎么转化为程序？这个框图是给人看的，是人与人之间交流算法思想时用的，往往只能用于手工模拟。由于先学流程图，学生还不会写代码，因此无法写出代码验证算法。如果先学算法语句，学会编写程序代码，则又淡化了算法思想的主导作用，违背了高中数学算法教学的初衷：重在理解算法思想，不要上成程序设计课。这就是算法思想与程序实现之间的结构性矛盾：从逻辑上讲，先有算法思想，再编程实现；但从技术上讲，先要编写程序，才能承载算法。这样就陷入了类似于先有“鸡”还是先有“蛋”的“怪圈”。

综合上述情况，算法教学在高中是很难有效开展的。那么，算法教学的出路何在？

画程软件破解编程教学难点

算法思维的本质是抽象和自动化。算法中的抽象属于人的思维范畴，可使用图符系统（如流程图）或形式化语言（如伪代码）来表达，当然，也可以直接用自然语言表达，但最终要落实在能够由机器自动化执行上。算法思维连接“人”和“机器”，为确保机器的自动化，必须在抽象过程中进行精确无歧义、人易懂易操作、机器也能执行的符号标记。此时此刻，我们渴望有一种“翻译工具”，能把这种抽象的符号系统，直接“翻译”为计算机能执行的软件，实现从“抽象”到“自动化”的软着陆。

自然语言是人的语言，但机器不懂（随着人工智能的发展，将会有改善）；伪代码是意在跨越各种计算机语言而提出的一种通用的、简明的文字符号系统，书写伪代码，实际上需要有程序思维和代码基础，所以不太适合初学者，而且伪代码并不能被计算机执行；计算机程序设计语言，是机器能懂的语言，虽然经过多轮迭代进化，计算机语言已经离人类语言越来越近了，但对初学者而言，中间仍有巨大的鸿沟。怎么顺利跨越这道鸿沟呢？

探究算法教学，其实也就是三个基本步骤：第一步，从分析问题得到用纸和笔分步骤可实现的通用算法，可称为纸笔算法；第二步，把用自然语言描述的纸笔算法转为用流程图表达；第三步，把流程图翻译为程序代码实现算法。高中数学“算法初步”教学，往往实现了前两步，无力实现第三步，倒在了算法被实证检验的最后一公里，使教学最终沦为令学生厌烦的“纸上谈兵”。高中信息技术课程中的“算法与程序设计”教学，则往往走向另一个极端：为了“解决问题”，常常舍弃算法构思与流程图，即抛弃了前两步，直接编写代码，至于为什么要这么写代码，常常无法向学生讲清楚，而且若代码较长，学生更接受不了，编程成为无源之水、无本之木。

综合两者，理想的算法教学是，第一步是根基，不可偏废，只能通过启迪学生数学分析能力、抽象逻辑思维能力、建立数学模型等来达成；第二步要易于用计算机软件实现；第三步则要由计算机软件自动实现。如果学生能用拖拽图标的方式轻松地绘制流程图，系统能够根据流程图和学生键入的信息自动生成程序代码，那么在研究、设计算法时，就能暂时不理会程序语言代码和实现的细节，只需专注于算法思想，这样就大大降低了算法入门的门槛。显然，教师需要一个算法教学的工具平台，来辅助解决两个问题：一是快捷方便地绘制、修改流程图，二是自动编程实现算法、验证算法。

“画程软件”应运而生。“画程”，寓意“用画图（流程图）的方式画出程序来”。画程软件能把流程图自动翻译为程序代码（支持Python，Java，C，C++，VB，QB等六种计算机高级语言），能编译（或解释）运行实现算法，这样就使原来的算法教学的三步变成了两步：第一步，设计算法（用自然语言表示）；第二步，用画程软件画出流程图，而这个流程图是可以执行的。画程软件避免了一些教师上机操作底气不足的尴尬，解放了教师；降低了算法入门门槛，适合初学者，释放了学生；可轻而易举地改变算法，是学生自主研习算法的好工具，激活了课堂。该软件对电脑设备要求低，操作简单。因此，画程软件成为中小学普及编程教学的极好平台，使人人都能学会编程成为可能。

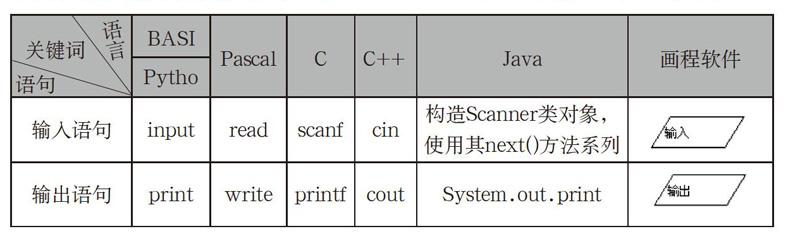
程序教学1.0和2.0，都是以“电脑”和“知识”为中心，学生要花大量精力学习它们的各种规则，才能小心谨慎地驾驭它们。令人“愤怒”的是，不同的计算机语言即使实现同样的功能，它们似乎也要故意使用不同的关键词和语法规则（如下表），使得人们总是为应该学习什么语言而纠结。

例如，要输入一个变量，就要根据不同的语言选择不同的“关键词”，是input，还是read，是scanf还是cin，抑或next（），还要严格遵守其语法规则，否则机器就罢工。

引入画程软件后，程序教学升级为3.0，教学以“学生”和“思维”为中心，学生只要会用纸和笔解决问题，写成步骤，就可以轻而易举地画出流程图，让计算机去编写代码并运行解决问题。如输入变量a，只需在“输入图标”中键入变量a就行了，至于怎么写出合法的输入语句，那是画程软件的事、机器的事。

画程软件实际应用案例

下面笔者以“有限验证考拉兹猜想”为例，说明画程软件的用法。

1.问题描述与算法设计

德国数学家考拉兹（Lothar Collatz）于1930年提出考拉兹猜想，又名3n+1猜想或冰雹猜想，是指对于每一个正整数（用变量n表示），如果它是偶数，则对它除以2，如果它是奇数，则对它乘3再加1，如此循环，最终都能得到1。

设计算法验证考拉兹猜想（当然只能是在有限的数据范围内验证），可用自然语言来描述算法：

第一步，輸入n（正整数）；

第二步，若n为偶数，则将其除以2，否则（n为奇数），将其乘以3后加上1，结果仍用n表示；

第三步，如果n等于1，退出到第4步，否则转回到第2步；

第四步，输出“考拉兹猜想成立！”。

2.用“画程”软件绘制流程图

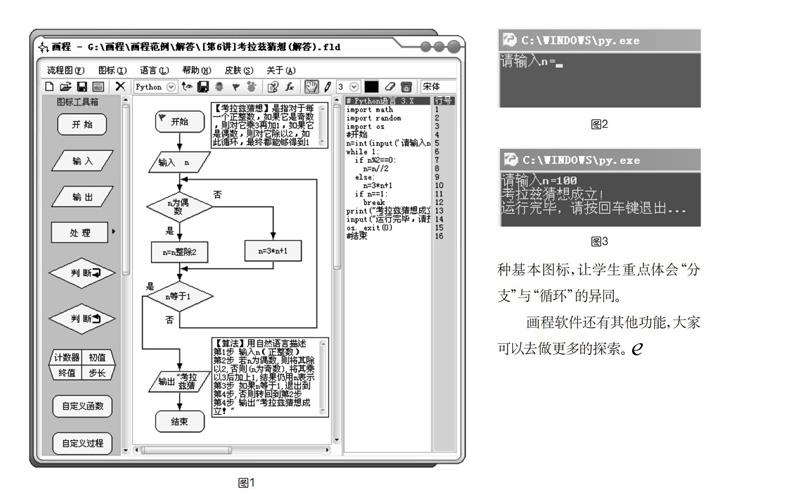
画程初始化时，就自动产生了一个只有“开始”图标和“结束”图标的（空的）流程图，它们之间有一根流程线相连。“开始”图标上有一个小红旗，表示当前主流程图（画程允许在一个流程图文件中有多个主流程图共存，以便于比较不同的算法，当然只能有一个为当前主流程图，如下页图1），拥有当前执行权。

第一步，拖入一个“输入”图标，在其内键入n。在画程中，输入变量的默认数据类型为浮点实型（float），本例此处应改为整型（int）：在刚才的“输入”图标的“输入”两字上点鼠标右键，在弹出的快捷菜单中单击“输入变量定为整数类型（int）”。

第二步，拖入一个“判断-分支”图标，内置条件怎么写？“n为偶数”如何用计算机的语言表达呢？显然，在画程支持的6种计算机语言里，取模运算的写法并不一致，为此，画程引入了一些“汉字关键字”，可以跨语言直接使用，如“取模”“整除”“π”“且”“或”“等于”“平方根（）”“绝对值（）”“随机整数（）”“返回”“为偶数”等，这样就能尽量实现“一次性画图，多语言通用”。直接键入条件n为偶数，在“是分支”里拖入一个“处理”图标，在“处理”图标里键入赋值语句n=n整除2。在“否分支”里拖入一个“处理”图标，键入赋值语句n=3*n+1。

第三步，这里有一个词非常关键——“转回”，也就是说，流程线要回到上面来，必须使用“判断-循环”图标，拖入一个“判断-循环”图标，条件怎么写呢？键入n等于1，“如果n等于1则退出”，所以这个“否”与“是”要交换，只要双击“是”或“否”就改变了。“否则，转回第2步”，要转到上面来，怎么操作呢？流程线不能拖动，可以把上面的分支（条件）结构拖拽到循环体内来（放在“判断-循环”图标“n等于1”的上面），这样就实现了“转回第2步”。

第四步，拖入一个“输出”图标，键入“考拉兹猜想成立！”。

第五步，运行程序，检验算法是否正确。

单击“保存流程图”工具，保存画好的流程图文件。单击“编译工具”，编译程序，成功之后，（以Python语言为例）弹出窗口（如图2）。

此时输入一个整数，如100，按回车（如图3）。

这个例子集聚了输入、输出、处理、判断-分支、判断-循环等五种基本图标，让学生重点体会“分支”与“循环”的异同。

画程软件还有其他功能，大家可以去做更多的探索。