引入拒识的最小风险弹道目标识别
赵振冲, 王晓丹
(空军工程大学防空反导学院, 710051, 西安)
弹道目标识别问题中,把弹头误判为诱饵比把诱饵误判为弹头所付出的代价要大得多。代价敏感方法就是为解决此类误分类代价不平衡问题而提出的。传统的分类方法进行了代价敏感拓展,例如代价敏感支持向量机[1-2],代价敏感贝叶斯[3-4],代价敏感神经网络[5],代价敏感决策树[6-7],代价敏感集成[8-9]等。Chatelain利用多目标优化算法构建受试者工作特征(ROC)前沿,然后依据最小贝叶斯风险确定给定代价矩阵下最优分类器[10];Bernard利用两两分解算法将Chatelain的方法推广到多类问题[11];Tapkana用代价矩阵修改近邻搜索方法和适应度函数,提出了代价敏感蜂群算法[12];Ju在粗糙集中引入测试代价和误分类代价,提出了一个通用的代价敏感粗糙集模型[13]。
弹道目标识别是一个时间上连续的过程,因此可以对当前类别属性不明确的目标进行拒识,在下一阶段再对其进行连续跟踪识别,以提高识别正确率并降低误判风险。构造可拒识分类器的关键在于拒识阈值的确定。刘传武等采用遍历的方法来确定使总体分类代价最小的拒识阈值[14-15];Giorgi通过对不同样本设置不同拒识阈值的方法来提高各类的识别正确率[16-17];郑恩辉等在风险最小的前提下采用最优化的方法来确定各类别的拒识阈值[18];Francesco在构建了最小化风险函数后借助于ROC曲线来确定两类目标的拒识阈值[19]。尽管以上方法均取得了不错的效果,但同样存在一些不足。前2种方法未考虑不同误分类代价的差异性,后2种方法的结果由于受训练样本的影响而出现较大随机性,即使在同一训练数据上,计算的结果也会出现较大差异。
基于以上分析,本文提出了一种新的引入拒识的最小风险弹道目标识别(ORC)方法,分析了ROC曲线及其特性,从类先验概率的角度推导其切线的斜率方程,构造了包含拒识代价的损失代价函数,推导了最小化代价风险时2类阈值所需满足的条件,并使其与ROC曲线切线的斜率相结合,确定了最小化损失代价的两类拒识阈值。
1 ROC曲线及分析
弹道目标识别可简化成只包含弹头和诱饵的两类分类问题,因此本文主要研究的是两类分类模型,而ROC曲线是一种用来评定两类分类器性能好坏的有效方法。
设I={(xi,yi)|xi∈Rd,i=1,2,…,N}为样本集合,yi为样本类别,yi={ω1,ω2}为样本类别。称第1类ω1为弹头(正类,阳性);第2类ω2为诱饵(负类,阴性)。令rtp为正类被正确分类的概率,即真阳性率(检测率);rtn为负类被正确分类的概率,即真阴性率;rfp为负类被错误分类的概率,即假阳性率(虚警率),rfn为正类被错分的概率,即假阴性率(漏警率)。ROC曲线是一个以rfp为横坐标,以rtp为纵坐标的二维图形,如图1所示,描述了两类分类器的检测率rtp和虚警率rfp之间的相互关系。曲线上每一个点表示在特定识别阈值下分类器的性能。越靠近左上角的点准确率越高,分类器性能越好。图1中虚线部分描绘了基于ROC曲线拟合得到的ROC凸包,它是对分类器在特定识别阈值时可能达到的最好性能的一种估计,可以用来对分类器进行局部寻优。
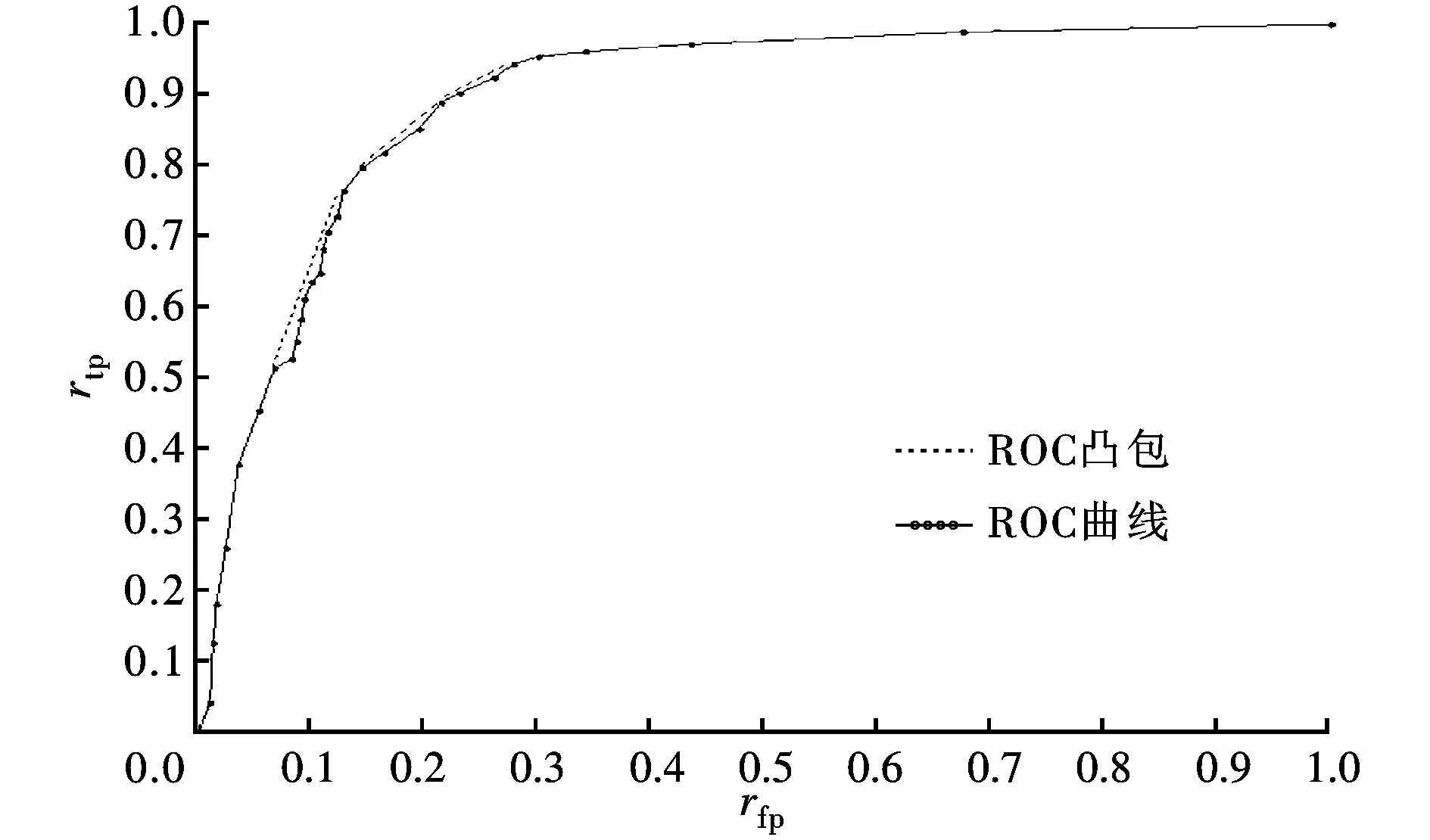
图1 检测率随虚警率变化的ROC曲线
设任意目标∀xi∈I,属于弹头和诱饵的后验概率分别为p(ω1|xi),p(ω2|xi),且p(ω1|xi)+p(ω2|xi)=1。设t∈[0,1]为对应于ω1的决策阈值,则最小错误率决策规则可表示为
(1)
假设p(ω1|xi)是xi的单调增函数,xi的维度为1,两类问题的后验概率如图2所示。对∀t∈[0,1],∃xt,使得对∀xi≥xt,p(ω1|xi)≥p(ω1|xt)=t。由此可知xt是决策阈值t的函数,设为
xt=g(t)
(2)
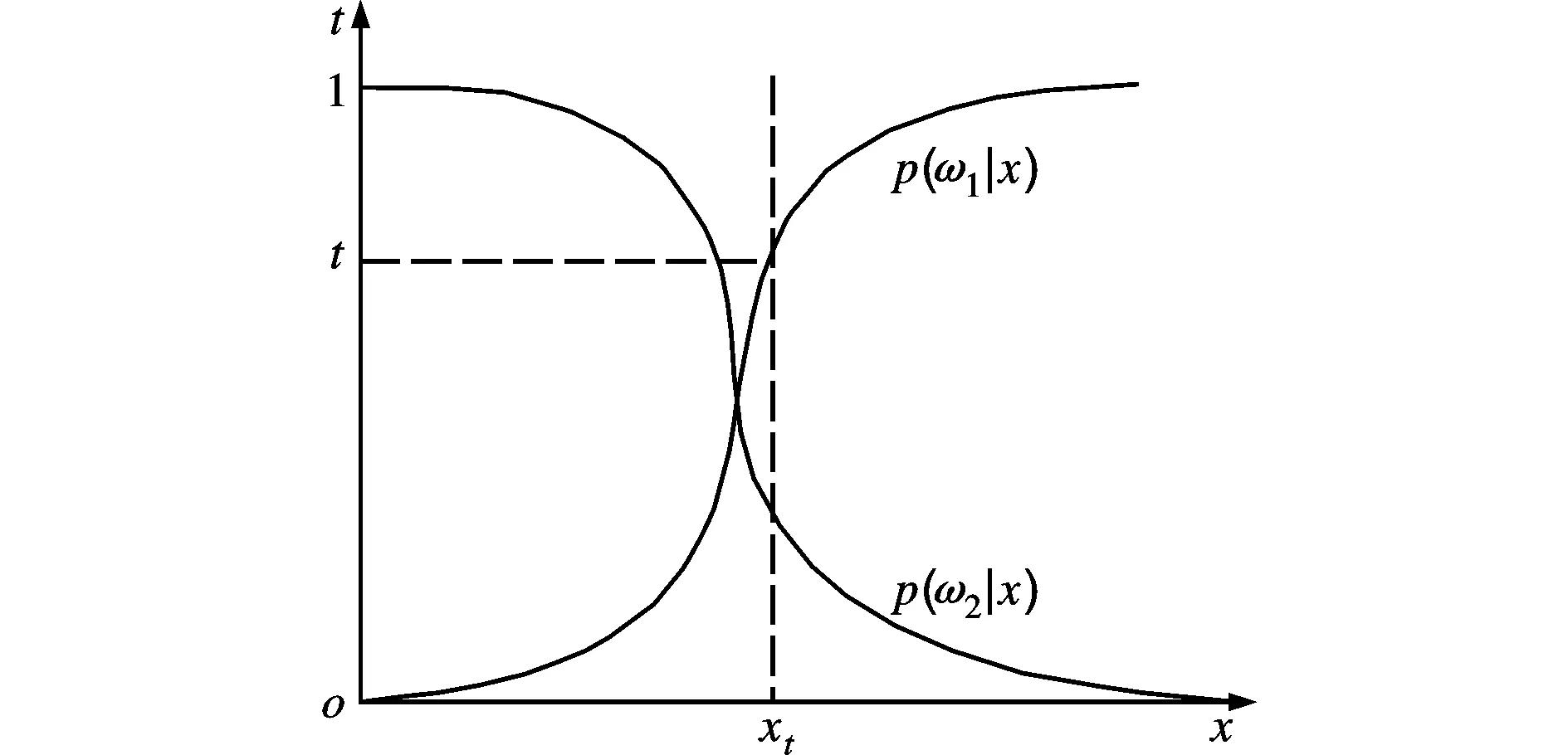
图2 两类问题的后验概率示意图
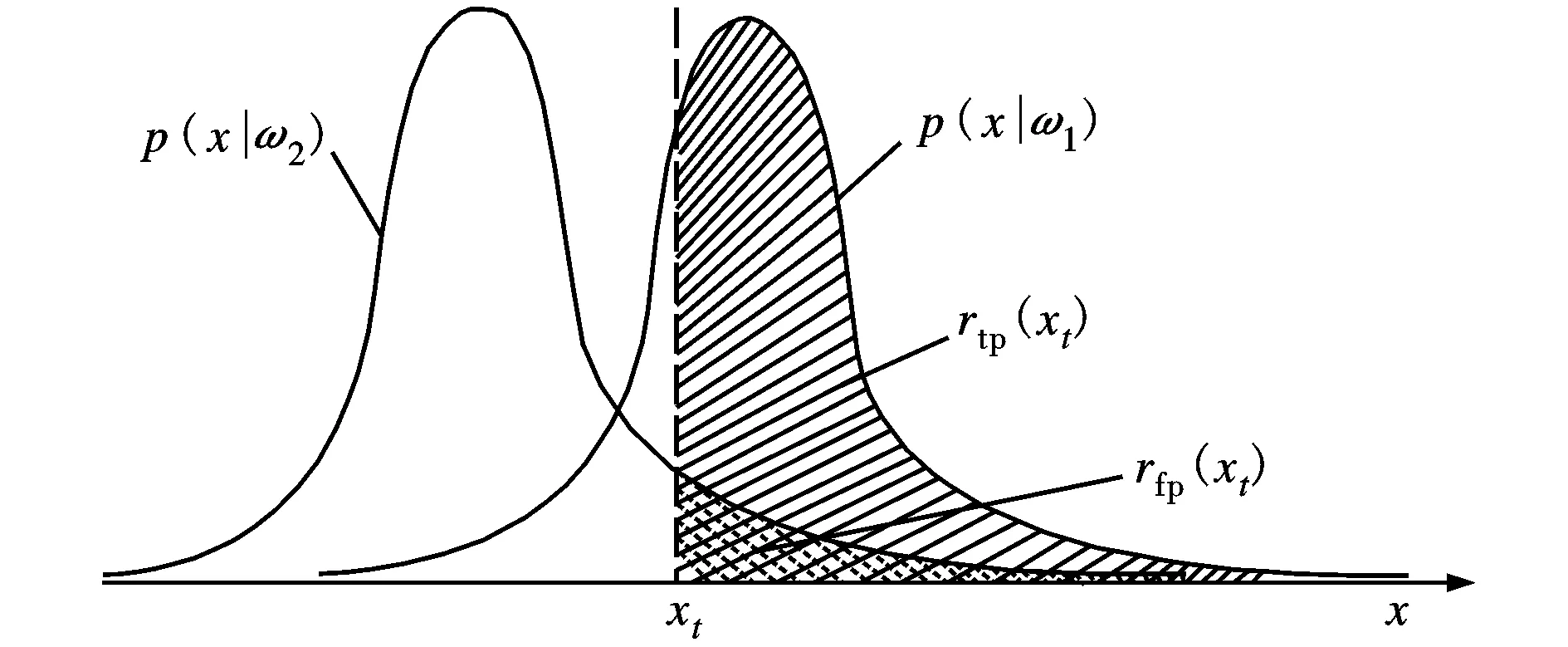
图3 一维情况下类条件概率密度示意图
图3为一维情况下两类目标的条件概率密度函数p(xi|ω1)和p(xi|ω2),其正类的检测率和虚警率可表示为
(3)
由式(3)可知,ROC曲线由rtp(xt)、rfp(xt)确定,则rtp对rfp求导可得
(4)
式中:K(xt)为ROC曲线上任一点的切线的斜率方程。综合式(1)、(4)可知,K是t的函数,设K=K(g(t))。
2 最优化拒识分类器
弹道目标识别是典型的非对称识别问题,利用代价敏感分类方法能够降低识别的整体风险。对应于式(1)的决策规则的代价矩阵可定义为
(5)
其中:Cij为将第i类识别为第j类的代价,由于把弹头误识为诱饵要比把诱饵误识为弹头的代价大得多,因此令C12>C21>C11=C22≥0。由式(3)可得
(6)
由式(3)、(6)可得,正、负类正确分类的概率分别为rtp(xt)p(ω1)和rtn(xt)p(ω2),正、负类错误分类的概率分别为rfn(xt)p(ω1)和rfp(xt)p(ω2)。根据式(5)任一决策阈值t下基于式(1)的决策规则的平均损失代价函数可表示为
Fcost(xt)=p(ω1)(C11rtp(xt)+C12rfn(xt))+
p(ω2)(C21rfp(xt)+C22rtn(xt))
(7)
式中:p(ω1)、p(ω2)分别是弹头和诱饵的类先验概率,且p(ω1)+p(ω2)=1。将式(2)带入式(7)得
Fcost=Fcost(g(t))
(8)
代价敏感分类可以形象地表示为把分类边界向误分类代价小的诱饵一类移动。由此带来的问题是对于诱饵会出现较高的误识率,考虑到弹道防御资源的有限性,这同样是不合适的。由于弹道目标识别是一个时间上连续的过程,需要在助推段、中段和再入段对其进行连续跟踪识别,因此在现阶段对风险大容易产生误分类的目标拒识,留给下一个时间点再对其进行跟踪识别更具实际意义。
设(t1,t2)为决策阈值对,且t1 (9) 图4 引入拒识的决策规则 此时式(3)和式(6)可变换为如下形式 (10) (11) 式中:xt1=g(t1),xt2=g(t2)。令rrn(xt1,xt2)为诱饵被拒识的概率,rrp(xt1,xt2)为弹头被拒识的概率,其表达式如下 (12) 对于拒识的样本,引入拒识代价Cr,此时式(5)中代价矩阵变换为如下形式 (13) 在弹道目标识别中,当前时刻拒识类别不确定的目标是为了利用下个或多个识别间隔的综合信息进行更为准确的识别,因此拒识的风险比每一种误分类代价都小才有意义,即C12>C21>Cr>C11=C22≥0。依据式(10)~(12),在阈值(t1,t2)下,正、负类正确分类的概率分别为rtp(xt2)P(ω1)和rtn(xt1)P(ω2),错误分类的概率分别为rfn(xt1)P(ω1)和rfp(xt1)P(ω2),正、负类拒分类的概率分别为rrp(xt1,xt2)P(ω1)和rrn(xt1,xt2)P(ω2),则根据式(13),此时的平均损失代价函数可表示为 Fcost(xt1,xt2)=p(ω1)(C11rtp(xt2)+C12rfn(xt1)+ (14) 将式(6)、(12)代入式(14)可得 Fcost(xt1,xt2)=p(ω1)(C11-Cr)rtp(xt2)+ (15) 式中:Δ=p(ω1)C12+p(ω2)C22。考虑式(4),将式(15)分别对rfp(xt1)和rfp(xt2)求偏导可得 (16) 令式(16)等于0,可得 (17) 要取得损失代价函数Fcost(xt1,xt2)的最小值,应使决策阈值对(t1,t2)对应ROC曲线上2点的切线的斜率满足式(17)。 设任一决策阈值p(ω1|xt)=t,则有 (18) 式中:p(xt)为目标概率密度函数。式(18)变换后得 (19) 考虑式(4)可知,ROC曲线上任一点的切线的斜率是决策阈值t的函数,即 (20) 将式(17)与式(19)联立,可得到2个最优拒识阈值 (21) 由式(21)可以得出,最小风险决策阈值对能够由代价矩阵(13)唯一确定。 根据代价矩阵的含义,设正确分类的代价为0,即C11=C22=0,则式(21)可以化简为 (22) 根据最小风险决策阈值(t1,t2)的含义有t1<0.5,t2>0.5,则Cr<0.5C12,Cr<0.5C21,即 Cr<0.5min(C12,C21) (23) 拒识代价应小于任一种误分类代价的一半,拒识才有意义。 本节利用两类目标的HRRP仿真数据验证所提方法的有效性。 实验数据来源于利用仿真软件计算得到的2类目标的动态一维距离像(HRRP)数据。2类目标分别为平底锥柱(弹头)和平底锥(诱饵),进动周期均为2 s,进动角为10°,雷达发射频率为8.75~10.75 GHz,采用步进雷达体制,频率步长为15.748 MHz,极化方式为水平极化,雷达采样频率为10 Hz。提取HRRP的能量聚集区长度特征、功率谱特征、幅度谱差分特征和频谱特征,4类特征组合构成维数为384的特征向量。 分类器采用支持向量机(SVM),核函数为径向基核函数。对于SVM输出利用Sigmoid函数转换成后验概率。用主分量分析法(PCA)对特征维数进行约减,并采用累积贡献率(Acr)的方法来确定约减后保留的主分量的维数,Acr变化区间为70%~94%,步长为0.02。采用10轮5倍交叉验证来计算各类的分类错误率和决策损失代价函数的大小。除本文方法外,利用循环搜索的方法来提取每一次实验中实际达到的最小分类代价(RLC)及其对应的决策阈值对,并以Francesco的方法[19]作为对比实验。RLC在搜索最优化拒识阈值时搜索步长设为0.1。Francesco用到的类先验概率采用样本比率进行近似估计。代价矩阵各参数设为 (24) 3.3.1不同分类方法代价Fcost的对比不同累积贡献率下3种方法的识别代价Fcost如图5所示。为了进一步对比3种方法的稳定性,图6给出了3种方法在未经约减的数据上采用10轮5倍交叉验证重复实验20次得到的分类代价。 图5 不同累积贡献率下3种方法的识别代价对比 图6 3种方法在20次独立重复实验中的分类代价 由图5可以看出,不同累积贡献率下,ORC方法的识别代价与RLC方法保持了高度的一致性,而RLC方法是可能达到的最好结果,说明ORC方法能够获得一个近似最优的结果,而Francesco方法产生的分类代价比ORC方法和RLC方法要大得多。由图6可以看出,不同的独立实验中ORC方法与RLC方法的识别代价相对稳定,Francesco方法的识别代价则波动较大,出现了较大的不稳定性。 3.3.2不同方法拒识阈值对的比较为了分析3种方法计算得出的阈值对之间的变化关系,图7给出了图6中每个点对应的决策阈值对。 图7 3种方法的决策阈值对变化趋势 由图7可以看出,Francesco方法的决策代价和决策阈值对出现无规律的波动,且有时在其确定的决策阈值对下分类器是无意义的。利用RLC方法可以确定最低的决策损失,但是其对应的决策阈值对同样出现无规律的变化。图7所示Francesco和RLC方法的阈值对的方差分别为0.08、0.21和0.0013、0.007 5。ORC方法不仅使分类造成的损失代价近似等于全局最小值,而且其决策阈值对由式(21)唯一确定,使得其具有很高的稳定性。 3.3.3不同方法识别率、漏警率和可靠性比较设正确分类样本数为ts,正类被正确识别的个数为tp,错误分类样本数为fs,正类识别为负类的个数为fn,总样本数为N。定义识别率为acc、可靠性为re、漏警率为rfn,其表达式如下 (25) 图8 3种方法的识别率对比结果 图9 3种方法的可靠性对比结果 图10 3种方法的漏警率对比结果 图8~10为3种方法在未经约减的数据上分别采用10轮5倍交叉验证重复实验20次得到的结果。由图8~10可以看出,ORC方法的性能接近于RLC方法的性能,在所有的实验次数中,识别结果没有出现大幅度的波动,说明ORC方法具有较好的识别性能和稳定性,证明了本文方法的有效性。Francesco方法识别结果的识别率、漏警率和可靠性均有明显的震荡,这是由于Francesco方法在训练过程中根据训练样本的不同以及得到ROC曲线的不完整性在确定阈值时有较大随机性导致的。 综上可知,ORC方法不仅能使分类风险接近于实际能达到的最小值,而且其决策阈值由代价矩阵决定,比较稳定,表现出了较好的性能。 本文提出了一种引入拒识代价的最小风险弹道目标识别方法。从类条件概率密度的角度推导了真阳性率、虚警率与决策阈值之间的关系,并进一步推导了ROC曲线上任意一点的斜率与决策阈值之间的关系;分析了代价敏感分类器及引入拒识代价的分类器,确定了代价损失函数,推导了代价最小化所需满足的条件,并将其与ROC曲线任意一点的切线斜率相结合,推导了最优化拒识阈值的确定方法。仿真实验表明,本文所提方法能够在保证代价最小的同时准确确定拒识阈值对,与传统方法相比,提高了稳定性和可靠性。 参考文献: [1]胡小生, 钟勇. 基于加权聚类质心的SVM不平衡分类方法 [J]. 智能系统学报, 2013, 8(3): 261-265. HU Xiaosheng, ZHONG Yong. Support vector machine imbalanced data classification based on weighted clustering centroid [J]. CAAI Transactions on Intelligent Systems, 2013, 8(3): 261-265. [2]DATTA S, DAS S. Near-Bayesian support vector machines for imbalanced data classification with equal or unequal misclassification costs [J]. Neural Networks, 2015, 70(12): 39-52. [3]JIANG L, LI C, WANG S S. Cost-sensitive Bayesian network classifiers [J]. Pattern Recognition Letters, 2014, 45(2): 211-216. [4]IBANEZ A, BIELZA C, LARRANAGA P. Cost-sensitive selective naïve Bayes classifiers for predicting the increase of the h-index for scientific journals [J]. Neurocomputing, 2014, 135(4): 42-52. [5]吕淑静. 基于代价敏感学习的手写邮编和地址识别 [D]. 上海: 华东师范大学, 2014: 23-45. [6]LI X, ZHAO H, ZHU W. A cost sensitive decision tree algorithm with two adaptive mechanisms [J]. Knowledge-Based Systems, 2015, 88(4): 24-33. [7]熊冰妍, 王国胤, 邓维斌. 分级式代价敏感决策树及其在手机换机预测中的应用 [J]. 山东大学学报, 2015, 45(5): 36-42. XIONG Bingyan, WANG Guoyin, DENG Weibin. Hierarchical cost sensitive decision tree and its application in the prediction of the mobile phone replacement [J]. Journal of Shandong University, 2015, 45(5): 36-42. [8]SUN Y M, KARNEL M S, WONG A, et al. Cost-sensitive boosting for classification of imbalanced data [J]. Pattern Recognition, 2007, 40(12): 3358-3378. [9]薛一哲, 王拓. 基于代价敏感Adaboost目标跟踪 [J]. 中国图像图形学报, 2016, 21(5): 544-555. XUE Yizhe, WANG Tuo. Object-tracking method based on improved cost-sensitive Adaboost [J]. Journal of Image and Graphics, 2016, 21(5): 544-555. [10] CHATELAIN C, ADAM S. A multi-model selection framework for unknown and/or evolutive misclassification cost problems [J]. Pattern Recognition, 2010, 43(3): 815-823. [11] BERNARD S, CHATELAIN C. The multiclass ROC front method for cost-sensitive classification [J]. Pattern Recognition, 2016, 52(4): 46-60. [12] TAPKANA P, ÖZBAKIRA L, KULLUKA S, et al. A cost-sensitive classification algorithm: BEE-Miner [J]. Knowledge-Based Systems, 2016, 95(2): 99-113. [13] JU H, YANG X, YU H, et al. Cost-sensitive rough set approach [J]. Information Sciences, 2016, 355/356(4): 282-298. [14] 刘传武, 张智军, 毕笃彦. 雷达目标自动识别系统的拒识新算法 [J]. 系统工程与电子技术, 2009, 31(8): 1846-1850. LIU Chuanwu, ZHANG Zhijun, BI Duyan. Novel refuse-recognition algorithm of radar automatic target recognition system [J]. Systems Engineering and Electronics, 2009, 31(8): 1846-1850. [15] 黄垚, 刘思颂, 孔瑞. 基于支持向量机的嵌入拒识代价的手写字符识别研究 [J]. 电子质量, 2011(4): 5-7. HUANG Yao, LIU Sisong, KONG Rui. SVM-based hand-written character recognition with reject option [J]. Electronics Quality, 2011(4): 5-7. [16] FUMERA G, ROLI F, GIACINTO G. Multiple reject thresholds for improving classification reliability [C]∥Proceedings of the Joint International Workshops on Advances in Pattern Recognition. Berlin, Germany: Springer-Verlag, 2000: 863-871. [17] FUMERA G, ROLI F, GIACINTO G. Reject option with multiple thresholds [J]. Pattern Recognition, 2000, 33(12): 2099-2101. [18] 郑恩辉, 徐欢. 嵌入非对称拒识代价的二元分类算法 [J]. 控制与决策, 2013, 28(6): 855-860. ZHENG Enhui, XU Huan. Binary classification algorithm with class-dependent reject cost [J]. Control and Decision, 2013, 28(6): 855-860. [19] TORTORELLA F. An optimal reject rule for binary classifiers [C]∥ Proceedings of the Joint International Workshops on Advances in Pattern Recognition. Berlin, Germany: Springer-Verlag, 2000: 611-620.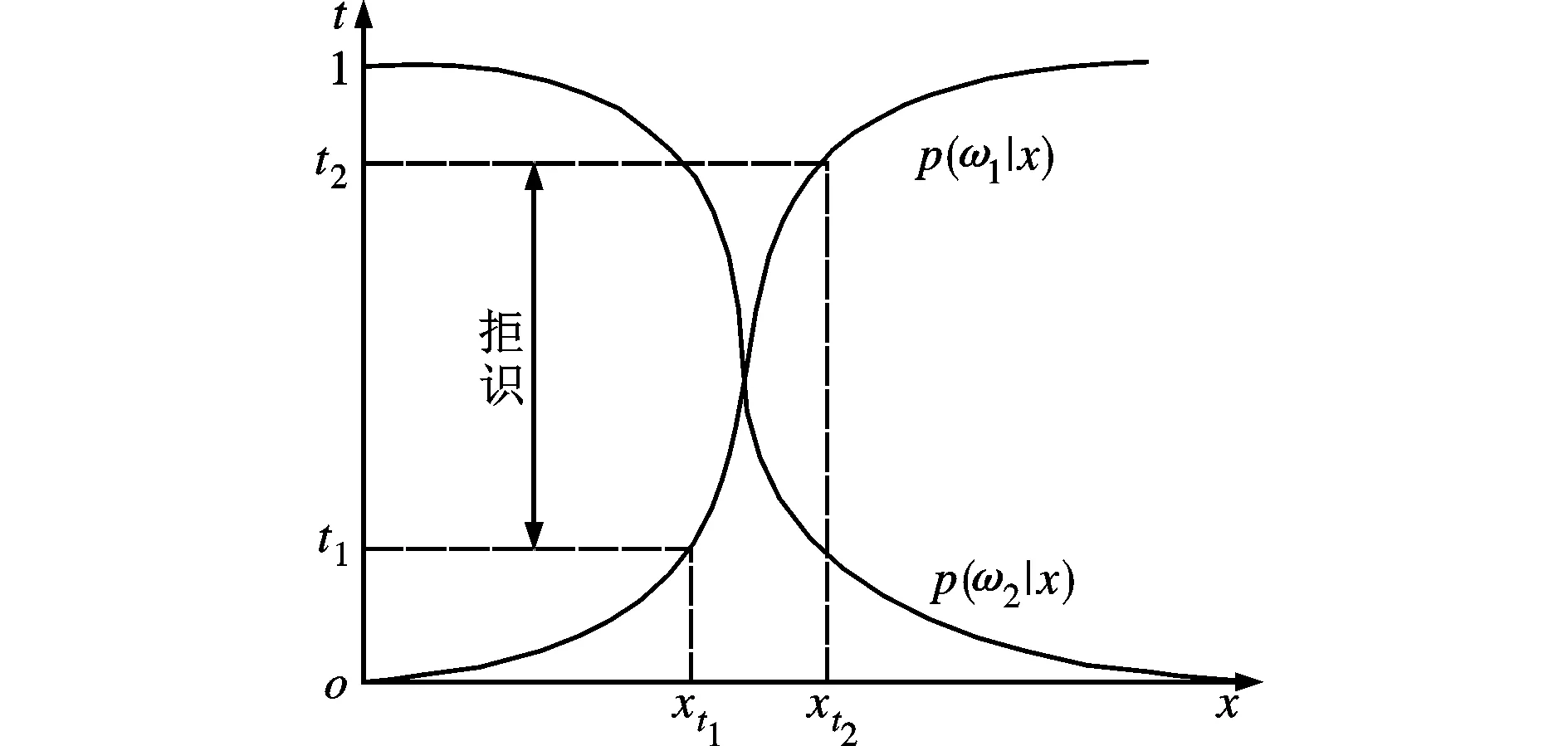
Crrrp(xt1,xt2))+p(ω2)(C21rfp(xt2)+
C22rtn(xt1)+Crrrn(xt1,xt2))
p(ω2)(C21-Cr)rfp(xt2)+p(ω1)(C12-Cr)rfn(xt1)+
p(ω2)(C22-Cr)rtn(xt1)+Cr=
p(ω1)(C11-Cr)rtp(xt2)+p(ω2)(C21-Cr)rfp(xt2)+
Δ-[p(ω1)(C12-Cr)rtp(xt1)+
p(ω2)(C22-Cr)rfp(xt1)]3 算法的实验验证与性能分析
3.1 实验数据
3.2 实验设计
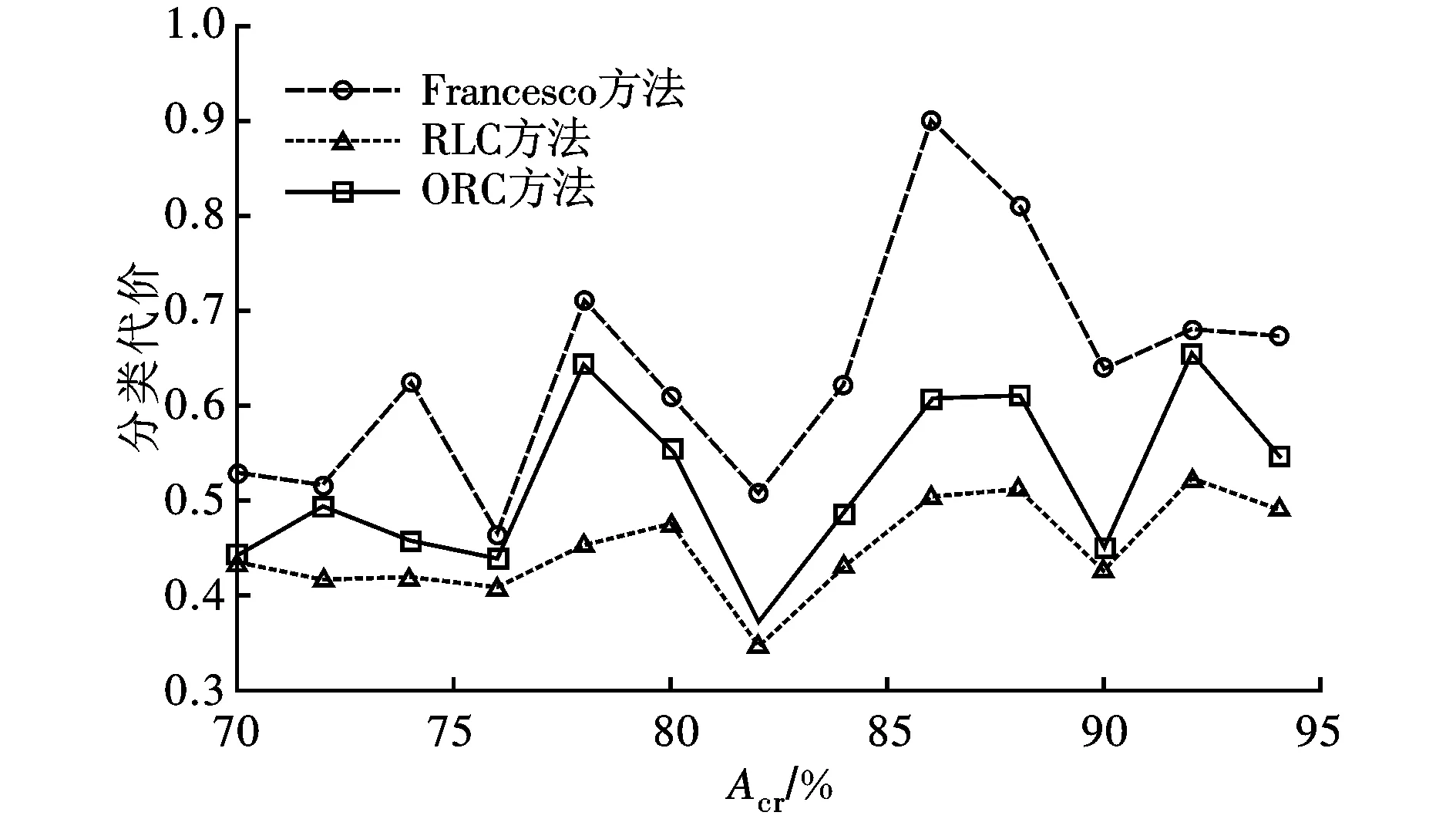
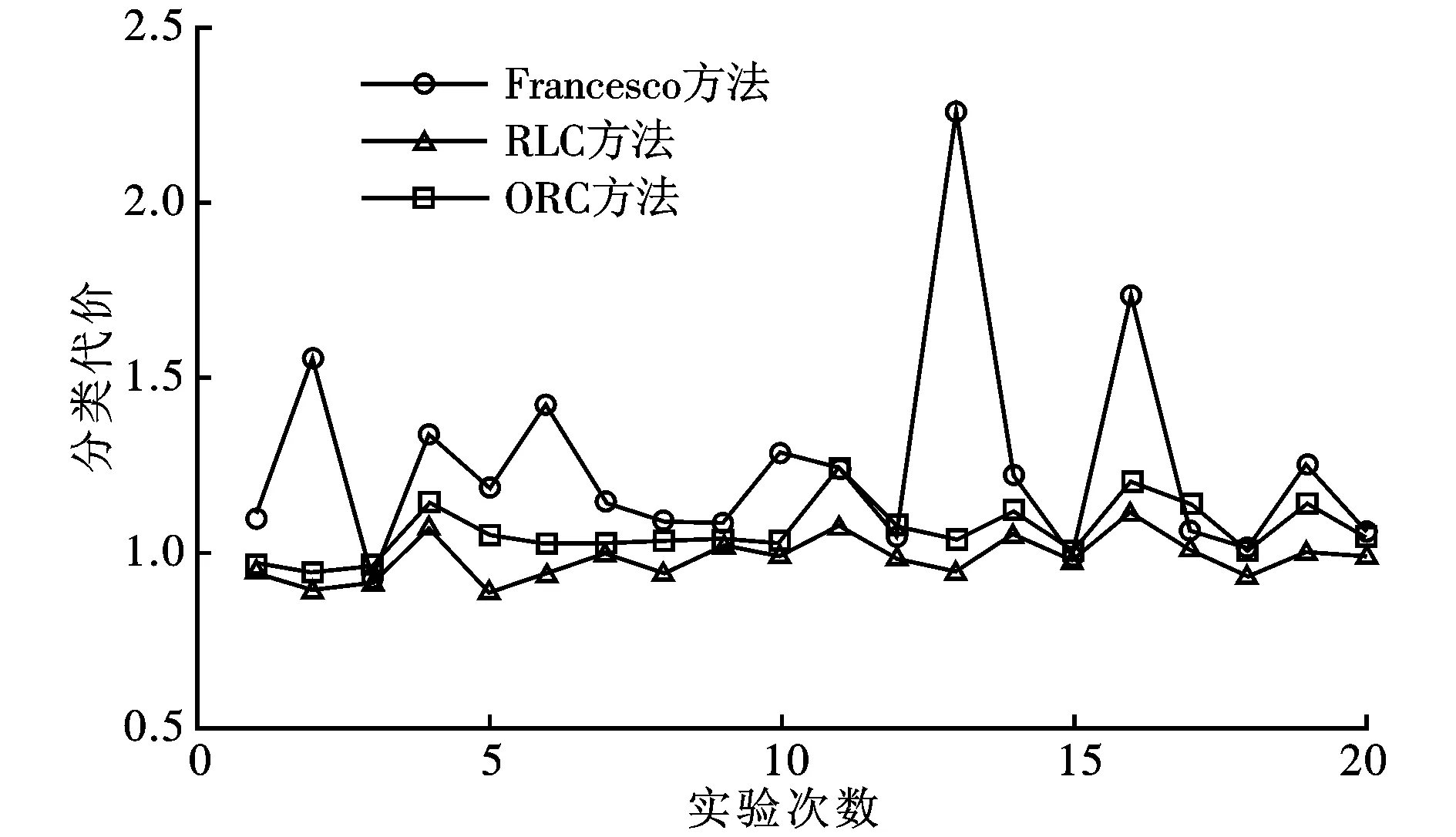
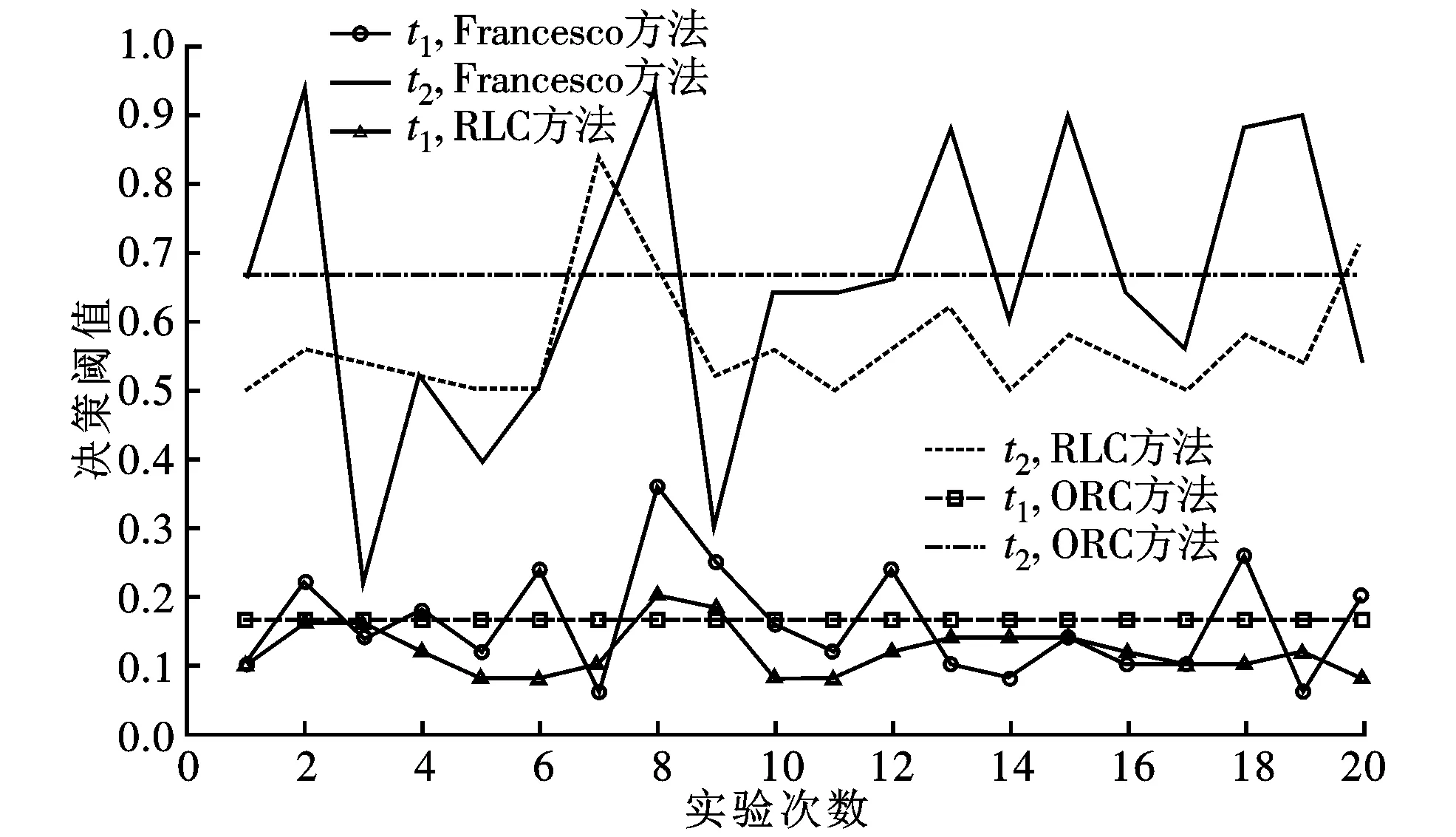
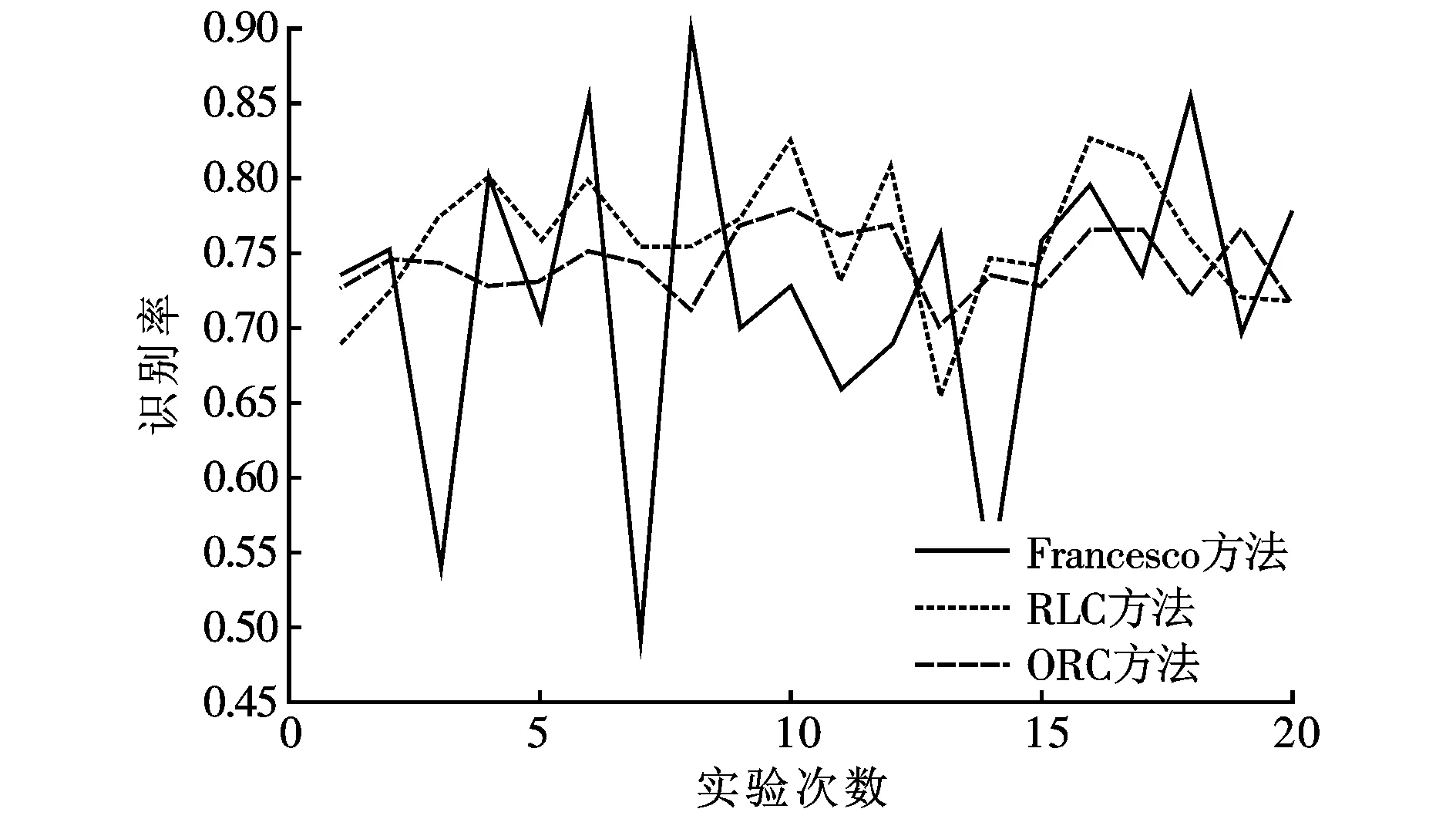
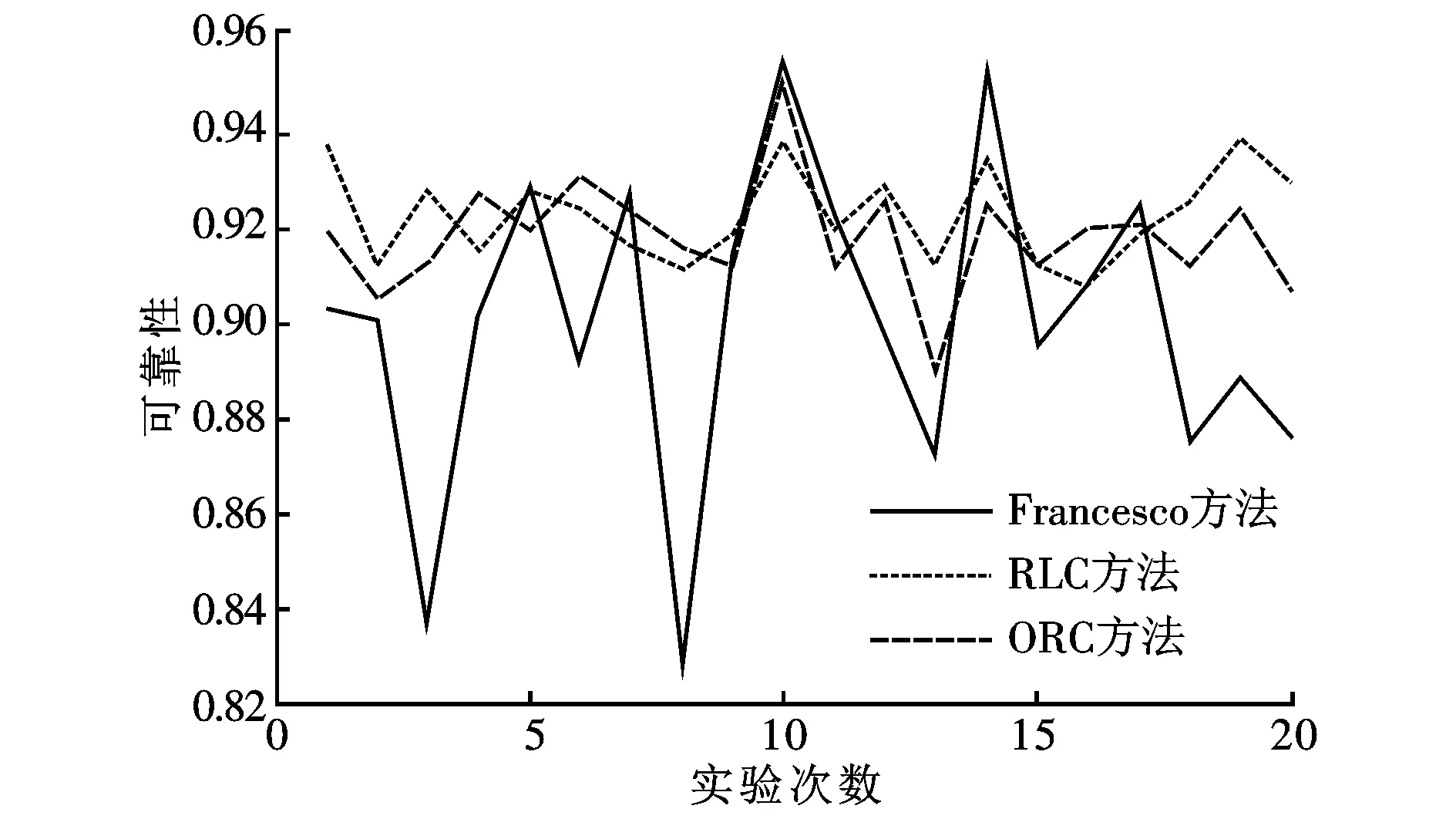
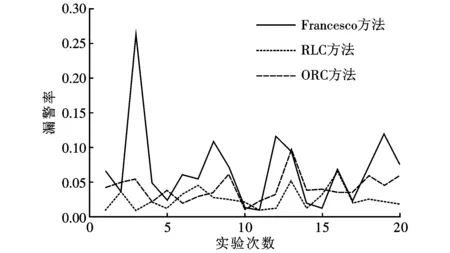
3.3 实验结果及分析
4 结 语

