500 kV自耦变压器直流偏磁振动特征提取与模式识别方法研究
吴晓文, 周卫华, 裴春明, 卢铃, 邹妍晖, 胡胜, 彭继文
(1.湖南省电力公司电力科学研究院, 410007, 长沙; 2.武汉南瑞集团有限公司, 430074, 武汉)
当特高压直流输电系统以单极大地回路方式或双极不平衡方式运行时,大量直流电流在流经的大地路径上产生电位差,如果交流变压器在附近运行,直流电流将通过变压器中性接地点及输电线路组成的通路流经变压器绕组,产生直流偏磁现象[1]。直流偏磁涉及的变压器数量众多,容易引起变压器噪声与振动加剧、铁心夹件松动、绕组松动与变形、绝缘受损、抗短路冲击能力下降以及局部过热等一系列问题,严重影响变压器的安全与稳定运行。因此,开展变压器直流偏磁检测具有重要意义[2-5]。
一般情况下,主要通过中性点电流检测判断变压器是否存在直流偏磁问题[6]。然而,由于500 kV自耦变压器绕组结构的特殊性,高压侧与低压侧共用一段绕组,即使采取电容隔直措施,偏磁电流仍有可能在220 kV与500 kV网络之间传递,造成隔离直流不彻底,无法完全消除直流偏磁对500 kV自耦变压器的影响。除了中性点直流,振动也是变压器直流偏磁状态检测的重要特征量,利用振动检测能够诊断出变压器直流偏磁问题[7]。文献[8]开发了变压器直流偏磁噪声与振动在线监测系统,但仅作为一般性监测使用,无法判断直流偏磁状态;文献[9]对比了直流偏磁前后振动信号时频域特征变化,但未对直流偏磁振动特征进行提取;文献[10]提出了直流偏磁振动奇偶次谐波比、延时互信息导数等特征参数并进行了验证,具有一定的参考意义,但未将以上特征进一步用于直流偏磁模式识别。
本文对直流偏磁前后500 kV自耦变压器振动信号时频域特征进行分析,采用奇偶次谐波比、频谱复杂度以及小波包能量等参数作为直流偏磁特征,并利用主成分分析方法(PCA)对特征去相关处理,提出基于最小二乘支持向量机(LS-SVM)的变压器振动特征模式识别方法,并对模式识别效果进行分析,为500 kV自耦变压器直流偏磁的有效监测提供了参考方法。
1 变压器直流偏磁振动特性分析
酒泉-湖南±800 kV特高压直流输电工程单极大地回线运行调试期间,对湖南省内受直流偏磁影响的某500 kV自耦变压器振动随调试工况进行连续检测,该变压器型号为东芝ODFPS-250000/500。分别采用B&K4534型加速度传感器与B&K4189型自由场传声器测量变压器振动与噪声信号,利用12通道B&K3053型采集模块进行同步信号采集,采样频率设置为32 768 Hz,利用B&K数据记录软件Time Data Recorder进行振动与噪声信号连续监测。变压器振动与噪声信号测点布置如图1所示。变压器箱体表面振动是其内部各振源综合作用的结果,加上箱体自身的线性与非线性结构特点,其表面振动分布十分复杂,不同测点位置振动幅值、相位乃至频谱分布均存在差异。因此,测点选择对于变压器振动测量结果具有十分重要的影响[11]。
变压器箱体表面测点所检测到的振动信号应该对其内部待检测对象缺陷的灵敏度较高,要求振动信号衰减小、信噪比高、受振动传播路径影响小。根据现有研究成果,一般在变压器油箱底部对应绕组位置设置振动测点[12]。由于此处主要关注变压器振动随偏磁电流的变化过程,对变压器表面振动强弱分布无具体要求,并结合现场变压器箱体表面实际结构,具体测试时,仅在变压器高压侧布置3个振动测点,如图1所示。其中,2号振动测点位于箱体中心线上,1号与3号测点位于2号测点两侧对称距离0.9 m处。此处,采用永磁体磁座将加速度传感器固定在变压器箱体表面较大平板区域、远离加强筋结构位置,以降低箱体结构非线性的影响。为了提高振动测试结果的代表性,利用3个测点振动幅值及频谱的平均值表征变压器的振动幅值及频谱。
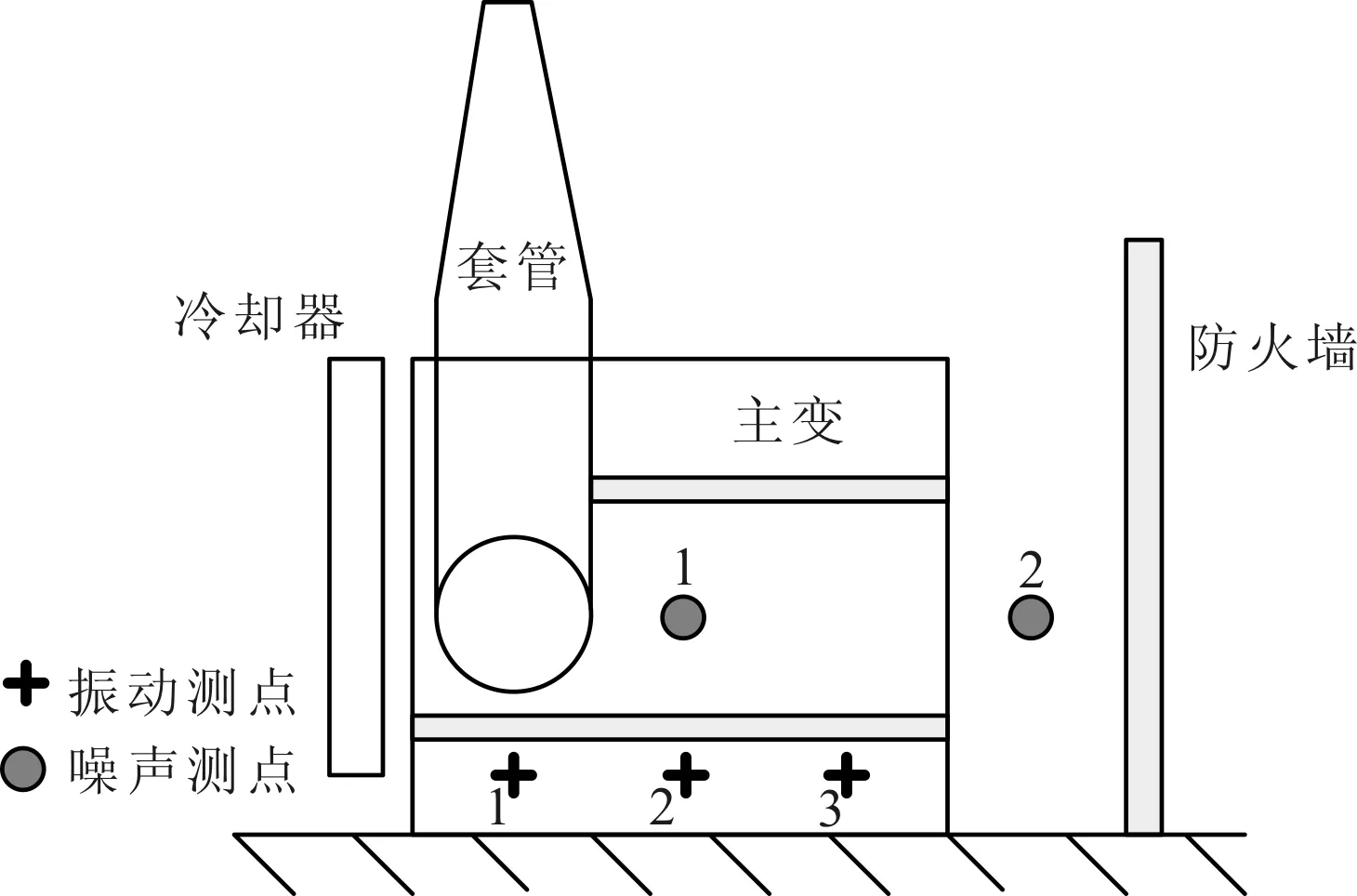
图1 500 kV自耦变压器振动与噪声信号测点布置图
特高压调试期间,150 min内变压器振动加速度随时间变化过程如图2所示。调试过程经历了输送功率600、1 300、2 000 MW等工况。调试前,变压器中性点处于直接接地状态。随着输送功率的逐渐增加,变压器振动加速度急剧增大,输送功率稳定后,振动加速度在一段时间内保持相对稳定,波动范围较小,振动加速度最大可达40.0 m/s2。在输送功率由600 MW上升至1 300 MW的过程中,中性点隔直装置自动投入,变压器中性点经电容接地,振动加速度急剧减小,但由于输送功率仍在继续增大,部分直流电流经低压绕组流入高压绕组,此时振动加速度仍高于正常水平。输送功率由1 300 MW逐渐上升至2 000 MW的过程中,变压器振动加速度迅速增大,经过一段时间的振动峰值后逐渐稳定在25.0 m/s2左右。由此可见,即使采取了电容隔直措施,仍无法消除自耦变压器的直流偏磁问题,此时通过中性点电流无法实现直流偏磁检测。
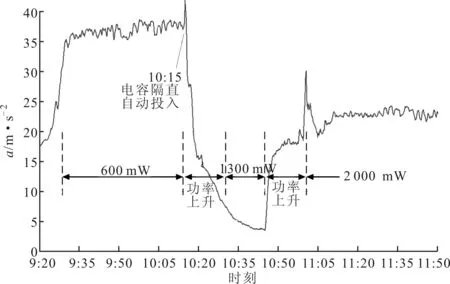
图2 变压器振动加速度变化过程
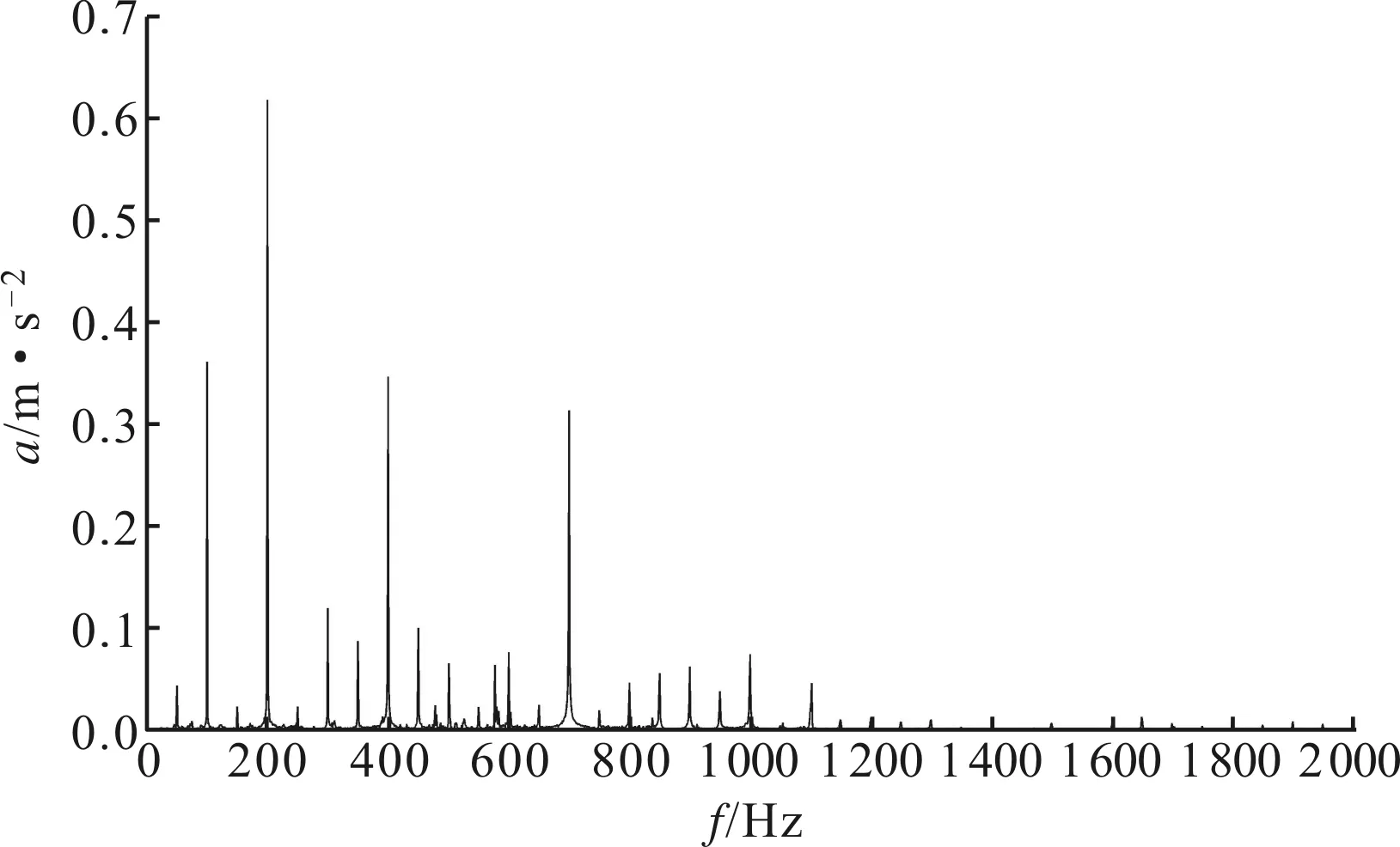
(a)直流偏磁前
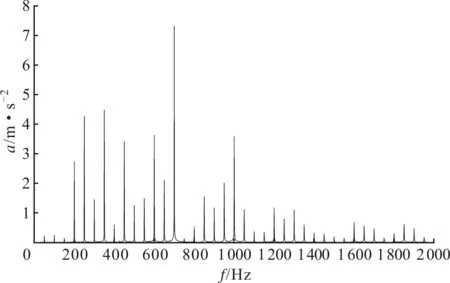
(b)直流偏磁后图3 直流偏磁前、后500 kV自耦变压器频谱分布
直流偏磁前后,变压器振动信号频谱如图3所示。正常条件下,变压器振动加速度a信号幅值为2.2 m/s2,频谱主要集中在1 kHz以内,信号能量主要集中在100、200、400以及700 Hz,其中主频200 Hz信号幅值为0.6 m/s2。发生直流偏磁后,中性点直流为10.6 A时,变压器振动信号幅值急剧增大至37.2 m/s2,较正常条件下增大约16倍。振动信号频谱分布较正常情况发生了显著变化,出现了较多高次谐波,振动信号频谱范围增加至2 kHz,且包含较多的50 Hz奇数倍谐波频率。信号主频发生变化,由200 Hz变为700 Hz,振动加速度信号出现幅值较高的1 kHz频率分量,信号幅值为3.6 m/s2,原本能量比重较高的100、200 Hz以及400 Hz频率分量幅值显著减小。由此可见,直流偏磁对于变压器振动特性具有十分严重的影响。
2 变压器直流偏磁振动特征提取
变压器振动信号为准平稳信号,短时间内时域信号幅值变化较小,因此主要从振动信号频域、时频域特性中提取直流偏磁特征参数。根据变压器直流偏磁前后振动信号频谱分布差异,分析原始特征,利用PCA方法消除原始特征之间的相关性,降低特征空间维数。
2.1 原始特征提取
由于变压器振动信号主要集中在2 kHz以内,此处仅从2 kHz范围内的频谱分布中提取原始特征。根据直流偏磁后变压器振动频谱中50 Hz奇数倍谐波频率幅值大幅增加、频率分量显著增多、不同频带能量发生显著变化等特点,提出奇偶次谐波比、频谱复杂度以及小波包能量等原始特征参数。
奇偶次谐波比表示频带范围2 kHz范围内,50 Hz奇数倍谐波频率分量能量与50 Hz偶数倍谐波频率分量能量的比值[11],具体可表述为
(1)
式中:A2i为信号50 Hz偶次谐波幅值;A2i-1为信号50 Hz奇次谐波幅值;N为2 kHz范围内信号50 Hz谐频数量。
变压器振动频谱复杂度主要表征频谱中频率成分的复杂程度,该值越低表明频谱在某些特征频率上能量越集中,越高则表明振动频谱能量越分散[13-14],频谱复杂度可按下式进行计算
(3)
(4)
式中:Ai为50 Hz第i次谐波幅值;Ri为50 Hz第i次谐频振动幅值比重;H为频谱复杂度。
利用小波包分析能够对变压器振动信号全频段进行时频分解,进而提取出不同频带信号能量,根据频带能量分布变化检测出变压器直流偏磁问题。对变压器振动信号进行e层小波包分解,将振动频谱分解为2e个等宽度频带。变压器振动信号S可以分解为[15-16]
(5)
式中:Sl为分解后的第l段振动信号。
小波包分解后,每个频带能量可表示为
(6)
式中:xlq为振动信号Sl的第q个离散点幅值。
小波包能量特征可表述为
(7)
2.2 振动特征主成分分析方法
奇偶次谐波比、频谱复杂度以及小波包能量构成变压器直流偏磁振动原始特征向量[Roe,H,T]。由于原始特征量之间存在相关性,采用主成分分析方法对原始特征去相关,并且降低特征空间维数,从而减少计算量。
设新特征ξ1,…,ξc为原始特征x1,…,xp的线性组合,每一个主成分所提取的信息量可用其方差度量,方差越大,该主成分所包含的信息越多。新特征的矩阵形式为[17-18]
Ax
(8)
(9)
式中:amn为第m个主成分中第n个原始特征对应的系数;am为第m个主成分归一化的系数矩阵;A为特征变换矩阵;x为原始特征矩阵。
在振动信号特征提取过程中,通常采用较少的主成分反映直流偏磁特征,从而降低特征空间维数并且消除数据中的随机噪声。前c个主成分所代表数据的累积方差贡献率为
(10)
(11)
式中:λm为第m个主成分ξm的方差;Σ为原始特征矩阵x的协方差矩阵。
在多数情况下,振动数据中的大部分信息集中在少数几个主成分上,通过事先确定主成分方差贡献率r的数值确定所需新特征的数量。
3 直流偏磁振动特征模式识别方法
支持向量(SVM)是一种基于统计学习理论的新型机器学习方法,具有良好的泛化能力,能有效处理小样本问题,不存在一般神经网络的局部极值问题。在SVM的基础上,LS-SVM将二次规划问题转化为线性方程组求解问题,加快了计算速度,具有良好的求解性能[19]。此处选取LS-SVM方法对变压器直流偏磁振动特征进行模式识别。
假设存在训练数据集{xk,yk}(k=1,2,…,M),其中,xk为输入样本数据,yk∈{-1,1}为分类类别,N为样本数。支持向量机分类器满足如下条件[19]
yk[ωTφ(xk)+b]≥1
(12)
分类超平面为
f(x)=ωTφ(x)+b
(13)
式中:ω为超平面法向量;b为偏置项;φ(x)为原始空间到高阶空间的非线性映射。
引入松弛变量εk与正规化参数γ,根据结构风险最小化原则,计算ω与b可转化为求解如下最小化问题[20]
(14)
约束条件为
yk[ωTφ(xk)+b]=1-εk
(15)
引入Lagrangian函数
(16)
式中:αk为Lagrangian乘子。
根据Karush-Kuhn-Tucker(KKT)条件,等式优化约束条件为[21]
(17)
消去ω与ε后,得到的线性问题如下
(18)
式中:I为单位矩阵;同时有
(19)
应用Mercer条件后,LS-SVM分类器可表述为
(20)
式中:Ψ(·,·)为核函数。此处采用径向基(RBF)核函数
Ψ(x,xk)=exp{-‖x-xk‖2/(2σ2)}
(21)
式中:σ为内积函数参数。
4 振动特征与模式识别效果分析
4.1 直流偏磁振动特征分析
对直流偏磁前后1 min内的变压器振动信号进行检测,分析奇偶次谐波比、频谱复杂度、小波包能量特征的变化规律,如图4所示。具体分析时,采用db4小波包、shannon熵进行4层小波包分解。
由图4a可以看出,直流偏磁前后变压器振动奇偶次谐波比特征发生显著变化,且变化过程与变压器振动幅值变化过程保持良好的一致性。偏磁发生前,奇偶次谐波比特征数值位于0.3范围内;偏磁发生后,该数值迅速增大,波动范围位于0.7~0.8范围内。图4b给出了直流偏磁前后频谱复杂度特征参数的变化过程,可以看出,频谱复杂度特征同样发生了较为显著的变化,变化过程与变压器振动幅值基本相似,但该特征的波动性较为明显,特征灵敏度较高。图4c给出了直流偏磁前后变压器振动小波包能量特征变化情况。根据小波包分解特点,小波包1~8为低频段,变压器振动频谱主要集中在该频段范围内。直流偏磁前,低频段小波包1与小波包2能量相对较高,其余频段能量较低。直流偏磁后,小波包3~8能量急剧增大,幅值均高于正常状态。因此,小波包能量特征可作为判断变压器直流偏磁状态的特征量。
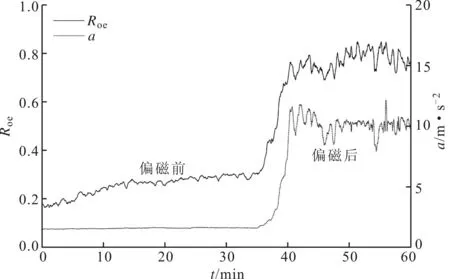
(a)Roe
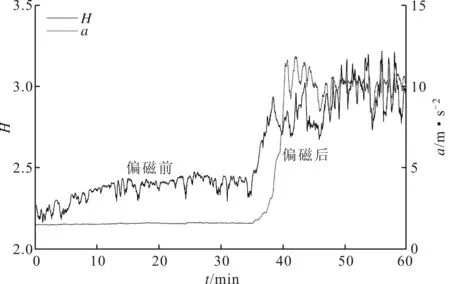
(b)H
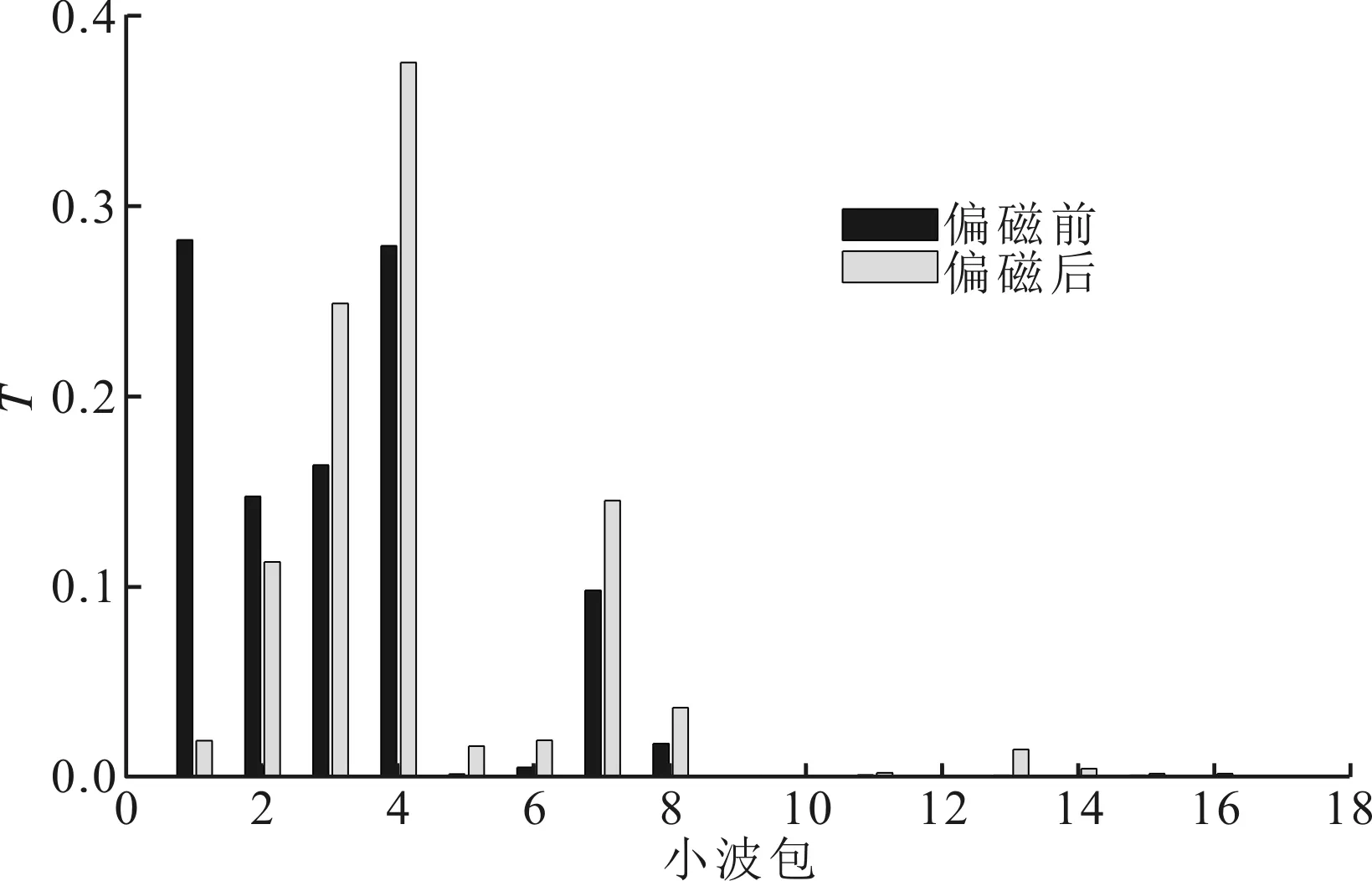
(c)小波包能量图4 直流偏磁前后振动特征变化情况
4.2 直流偏磁振动特征主成分分析
奇偶次谐波比、频谱复杂度、小波包能量特征共同构成18维直流偏磁振动特征向量。对直流偏磁调试期间500 kV自耦变压器振动进行检测,其中一部分测试数据作为训练样本,计算出每个样本的特征参数并构成原始特征向量,对该特征向量进行主成分分析,从而提取出主要特征。
选取126组样本进行计算,其中108组样本为直流偏磁样本,其类别采用“1”表示,包括直流输送功率为600、2 000、2 100 MW时的样本数据各36组;18组为正常样本,类别采用“-1”表示。一般而言,累积方差贡献率取为85%时,所提取出的主成分已蕴涵原始特征量的主要信息。
计算变压器直流偏磁振动原始特征协方差矩阵的特征值,并对特征值由大到小进行排序,计算出各主特征的累积方差贡献率为

(22)
可以看出,经过主成分分析后,第2个主要特征的累积方差贡献率已经高达97.9%,已能够充分反映出原始特征所代表的所有信息,达到了原始特征降维目的,降低了后续模式识别过程的计算量。
计算出特征变换矩阵为
(23)
利用特征变换矩阵计算出2维直流偏磁振动主特征,并用于模式识别分析。
4.3 LS-SVM模式识别结果与分析
利用LS-SVM对126组变压器直流偏磁振动数据的主成分分析结果进行训练,以形成特征分类器。训练过程中,需要确定径向基内积函数参数σ和正规化参数γ。为了确定最优的参数对(σ,γ),必须构造适合的参数选择模型。由于最小二乘支持向量机将优化问题转化为求解线性方程组,求解速度快,可以采用交叉验证方法进行参数选择。通过分析,选择参数对(10,0.2)可将变压器正常振动信号与直流偏磁振动信号正确区分,能够取得较为理想的分类结果。直流偏磁振动主特征分类以及相应的分类器计算结果如图5所示。
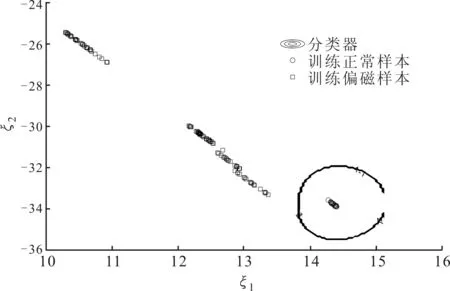
图5 LS-SVM特征分类训练结果
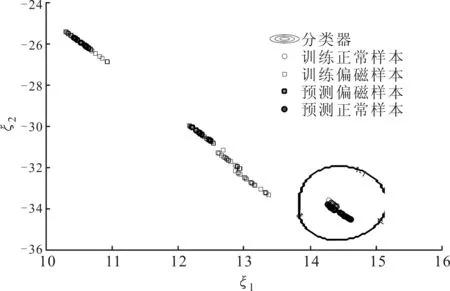
图6 LS-SVM直流偏磁预测结果
设置另外36组振动信号为待预测样本信号,其中18组为直流偏磁信号,18组未正常振动信号,对其进行主成分分析,利用图5中的分类器对主成分分析结果进行模式识别,识别效果如图6所示。可以看出,直流偏磁样本与正常振动信号样本分别位于分类器两侧,且与分类器的距离较远,利用上述分类器实现了变压器直流偏磁状态的准确识别,识别率达到100%,表明了基于PCA与LS-SVM方法应用于变压器直流偏磁振动状态检测的有效性。
5 结 论
本文提出了变压器直流偏磁特征参数,并利用主成分分析方法降低特征空间维数,采用LS-SVM实现变压器直流偏磁振动模式识别,主要得出如下结论:
(1)直流偏磁对变压器振动时频特性影响较大,即使采取隔直措施仍无法消除自耦变压器的直流偏磁现象。
(2)奇偶次谐波比、频谱复杂度以及小波包能量等原始特征参数能够反映变压器直流偏磁问题,采用PCA方法可有效降低原始特征空间维数。
(3)通过调整核函数参数对,利用LS-SVM方法能够对变压器直流偏磁振动主特征进行有效识别,所提出的方法为变压器直流偏磁检测提供了技术参考。
参考文献:
[1]JIANG Wei, WU Guangning, XIAO Hua, et al. Effects of transformer DC bias and the relationship between UHV DC grounding current and grounding resistances [J]. High Voltage Engineering, 2008, 34(12): 2530-2535.
[2]皇甫成, 阮江军, 张宇, 等. 变压器直流偏磁的仿真研究及限制措施 [J]. 高电压技术, 2006, 32(9): 117-120.
HUANGFU Cheng, RUAN Jiangjun, ZHANG Yu, et al. DC magnetic bias induced current effects on transformer and restricting methods [J]. High Voltage Engineering, 2006, 32(9): 117-120.
[3]杨晓辉, 王丰华, 段若晨, 等. 500 kV电力变压器直流偏磁耐受性能的仿真研究 [J]. 电力系统保护与控制, 2014, 42(14): 60-66.
YANG Xiaohui, WANG Fenghua, DUAN Ruochen, et al. Simulation study of DC bias enduring ability of 500 kV power transformer [J]. High Voltage Engineering, 2014, 42(14): 60-66.
[4]苑舜, 王天施. 电力变压器直流偏磁研究综述 [J]. 高压电器, 2010, 46(3): 78-87.
YUAN Shun, WANG Tianshi. Summary of research on transformer DC magnetic bias [J]. High Voltage Apparatus, 2010, 46(3): 78-87.
[5]马为民. 换流变压器中直流偏磁电流的计算 [J]. 高电压技术, 2004, 30(11): 39-49.
MA Weimin. DC biasing current in converter transformer [J]. High Voltage Engineering, 2004, 30(11): 39-49.
[6]张红跃, 张清枝, 熊章学, 等. 采用交流互感器测量变压器中性点直流分量的方法 [J]. 电力系统保护与控制, 2013, 41(16): 97-102.
ZHANG Hongyue, ZHANG Qingzhi, XIONG Zhangxue, et al. A method of measuring neutral point DC component of transformer using AC transformer [J]. Power System Protection and Control, 2013, 41(16): 97-102.
[7]吴晓文, 周年光, 胡胜, 等. 分布式变压器直流偏磁多状态量检测技术研究 [J]. 科学技术与工程, 2017, 17(10): 202-207.
WU Xiaowen, ZHOU Nianguang, HU Sheng, et al. Distributed multi-physics measurement technology investigation of DC bias in transformer [J]. Science Technology and Engineering, 2017, 17(10): 202-207.
[8]马海. 基于直流偏磁影响下变压器本体振动与噪声的在线监测 [D]. 长沙: 长沙理工大学, 2013.
[9]陈青恒, 马宏彬, 何金良. 直流偏磁引起的500 kV电力变压器振动和噪声的现场测量与分析 [J]. 高压电器, 2009, 45(3): 93-95.
CHEN Qingheng, MA Hongbin, HE Jinliang. Field monitoring and analysis on vibration and noise of 500 kV electrical transformer under DC current biasing [J]. High Voltage Apparatus, 2009, 45(3): 93-95.
[10] 郭洁, 黄海, 唐昕, 等. 500 kV电力变压器偏磁振动分析 [J]. 电网技术, 2012, 36(3): 70-75.
GUO Jie, HUANG Hai, TANG Xin, et al. Analysis on 500 kV power transformer vibration under DC magnetic biasing [J]. Power System Technology, 2012, 36(3): 70-75.
[11] 朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究 [J]. 西安交通大学学报, 2015, 49(6): 115-125.
ZHU Yeye, JI Shengchang, ZHANG Fan, et al. Vibration mechanism and influence factors in power transformers [J]. Journal of Xi’an Jiaotong University, 2015, 49(6): 115-125.
[12] RIKARDO S A, BAMBANG C B, SUMARYADI C, et al. Vibration monitoring on power transformer [C]∥International Conference on Condition Monitoring and Diagnosis, Beijing, China, 2008.
[13] 师愉航. 变压器声纹特征研究及噪声评估系统开发 [R]. 西安: 西安交通大学, 2017: 64-66.
[14] 汲胜昌, 张凡, 钱国超, 等. 稳态条件下变压器绕组轴向振动特性及其影响因素 [J]. 高电压技术, 2016, 42(10): 3178-3188.
JI Shengchang, ZHANG Fan, QIAN Guochao, et al. Characteristics and influence factors of winding axial vibration of power transformer in steady-state operation condition [J]. High Voltage Engineering, 2016, 42(10): 3178-3188.
[15] 吴晓文, 周年光, 裴春明, 等. 特高压交流变电站可听噪声分离方法 [J]. 高电压技术, 2016, 42(8): 2625-2632.
WU Xiaowen, ZHOU Nianguang, PEI Chunming, et al. Separation methodology of audible noise of UHV AC substations [J]. High Voltage Engineering, 2016, 42(8): 2625-2632.
[16] 汲胜昌, 刘味果, 单平, 等. 小波包分析在振动法监测变压器铁芯及绕组状况中的应用 [J]. 中国电机工程学报, 2001, 21(12): 24-27.
JI Shengchang, LIU Weiguo, SHAN Ping, et al. The application of the wavelet packet to the monitoring of the core and winding condition of transformer [J]. Proceedings of the CSEE, 2001, 21(12): 24-27.
[17] 李自品, 舒乃秋, 李红玲, 等. 绝缘子污秽放电的声发射核主成分诊断法 [J]. 高电压技术, 2012, 38(11): 3008-3014.
LI Zipin, SHU Naiqiu, LI Hongling, et al. Acoustic emission diagnosis method of insulator’s pollution discharge based on kernel principle component analysis [J]. High Voltage Engineering, 2012, 38(11): 3008-3014.
[18] 张学工. 模式识别 [M]. 第3版. 北京: 清华大学出版社, 2013: 161-167.
[19] 焦尚彬, 刘丁, 郑岗, 等. 基于最小二乘支持向量机的绝缘子等值附盐密度预测 [J]. 中国电机工程学报, 2006, 26(2): 149-153.
JIAO Shangbin, LIU Ding, ZHENG Gang, et al. Forecasting the ESDD of insulator based on least square support vector machine [J]. Proceedings of the CSEE, 2006, 26(2): 149-153.
[20] 李红玲, 文习山. 绝缘子污秽放电声发射的统计指纹分析 [J]. 高电压技术, 2010, 36(11): 2705-2710.
LI Hongling, WEN Xishan. Statistical fingerprint analysis for contaminated insulator acoustic emission signals [J]. High Voltage Engineering, 2010, 36(11): 2705-2710.
[21] SUYEKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers [J]. Neural Processing Letters, 1999, 9(3): 293-300.

