采用品质因子优化和子带重构的共振稀疏分解滚动轴承故障诊断方法

陈保家, 汪新波, 严文超, 田红亮, 肖文荣, 陈法法, 刘浩涛

(1.三峡大学湖北省水电工程施工与管理重点实验室, 443002, 湖北宜昌; 2.三峡大学湖北省水电机械设备设计与维护重点实验室, 443002, 湖北宜昌; 3.湖北三峡职业技术学院机电工程学院, 443000, 湖北宜昌)

滚动轴承故障的振动特性主要由轴承的转动、轴承结构、损伤形态、轴承与系统的传递路径等决定。当滚动轴承发生早期故障时,由损伤引起的冲击脉冲力不但会诱发轴承系统的高频固有振动,而且此高频振动的幅值还受到冲击脉冲力的调制[1]。振动信号中主要包含与转数相关的谐波成分、故障冲击成分以及背景噪声,大多表现出非线性和非平稳性,各成分振动信号存在中心频率相近、频带重叠的情形。滚动轴承故障诊断的关键是从故障诊断信号中分离出故障冲击成分,减少谐波及噪声的干扰,凸显故障特征。

傅里叶变换以信号表示为不同频率的平稳正弦波的线性迭加作为前提条件,缺乏对信号局部时频变化的精确描述。近年来,针对非平稳性、非线性信号的处理一直是机械故障诊断领域研究的热点。严如强等针对强背景噪声下的非平稳瞬态微弱信号,提出了一种融合连续小波变换和平稳子空间分析的信号分解方法,并应用于风力发电机齿轮箱故障诊断中[2];郑近德等提出了一种改进的经验模态分解(EMD)故障诊断方法,通过广义经验模态分解定义多种均值曲线,再采用改进的经验调幅调频分解和直接正交解调方法对最优本征模函数(IMF)分量进行解调,提高了分解和解调的精确性,抑制了端点效应的产生[3];Wang和Chen等分别对局部均值分解(LMD)方法的滤波特性和噪声影响进行了分析,给出了LMD波形和瞬时频率提取的信噪比阈值,并将LMD方法应用于旋转机组碰摩和电力机车走行部故障识别中[4-5];向家伟等以随机共振输出信噪比作为目标函数,利用人工蜂群算法搜索全局最优解,实现双稳系统参数的自适应调节,获得信噪比最大时的系统参数,从而实现从强噪声环境中检测出微弱信号[6]。

以上信号处理方法都是先通过解析表达式或者自适应方法将信号分解到多个频带区间,然后对特定频带进行故障特征提取从而达到诊断的目的。当谐波成分、故障冲击成分以及背景噪声的中心频率重叠时,不能通过一般的频带分解或线性滤波方法将其分开,可以考虑通过信号共振属性不同(即品质因子Q不同)对其进行信号分解。Selesnick提出了共振稀疏分解(RSSD)[7]方法,该方法可根据信号Q的不同,将复杂信号分解成由持续振荡成分组成的高共振分量和由瞬态冲击成分组成的低共振分量;黄文涛等利用遗传算法优良的寻优性能,自适应地优化RSSD方法中的品质因子,并将其应用于某行星增速齿轮箱中行星齿轮与行星架轴承的复合故障诊断中[8];张文义等采用RSSD方法将冲击脉冲从滚动轴承振动信号中分离出来,然后采用能量算子解调方法对其进行包络解调,获取冲击脉冲出现的周期,进而对滚动轴承故障进行诊断[9]。

现有的RSSD方法大多只分析分解后的低共振分量,假定低共振分量由瞬态冲击成分组成,而对于滚动轴承早期的微弱故障,不同共振属性的分量可能耦合程度较大,故障特征频率不占优时往往难以观察。同时RSSD方法没有类似于小波变换、EMD或LMD等方法的多尺度频带分析能力,对于瞬态冲击分量的信息挖掘能力体现不足。基于以上分析,本文提出了一种融合遗传算法品质因子参数优化、子带重构的RSSD方法和小波变换相结合的滚动轴承故障诊断方法,以RSSD方法所得到的低共振分量峭度作为优化目标函数,对高低品质因子组合进行优化选择;以能量分布特征对低共振分量进行主子带重构,减少噪声干扰以及凸显故障特征;对重构低共振分量进行小波分解,深度挖掘轴承故障特征信息。

1　信号共振稀疏分解

RSSD方法的基础是品质因子可调小波变换(TQWT)方法,其关键是构建品质因子可调小波。Selesnick在早期研究时探讨了二进制小波与一种过完备的有理膨胀小波(RADWT)[10]方法。其中,RADWT方法通过改变信号上下抽样q的大小获得不同的品质因子Q,使Q的选择范围增大,从而提高频率分辨率,该方法要求信号具有较大的信号长度。Selesnick进一步提出了TQWT方法,直接确定Q值及冗余因子r,根据振动信号的特性来选择Q,在应用时更加灵活。

1.1　可调品质因子小波变换

(1)

式中:γ表示冗余度。多层分解过程的本质是将一个信号依次通过高频带通滤波器至低频带通滤波器的过程,依靠分解滤波器组进行连续迭代。RSSD方法依据信号的共振属性不同把信号分解为具有不同振荡特性的成分,共振属性大小由Q值决定,尺度因子α、β由Q和γ来确定,利用一个两通道滤波器组进行多层分解与合成。

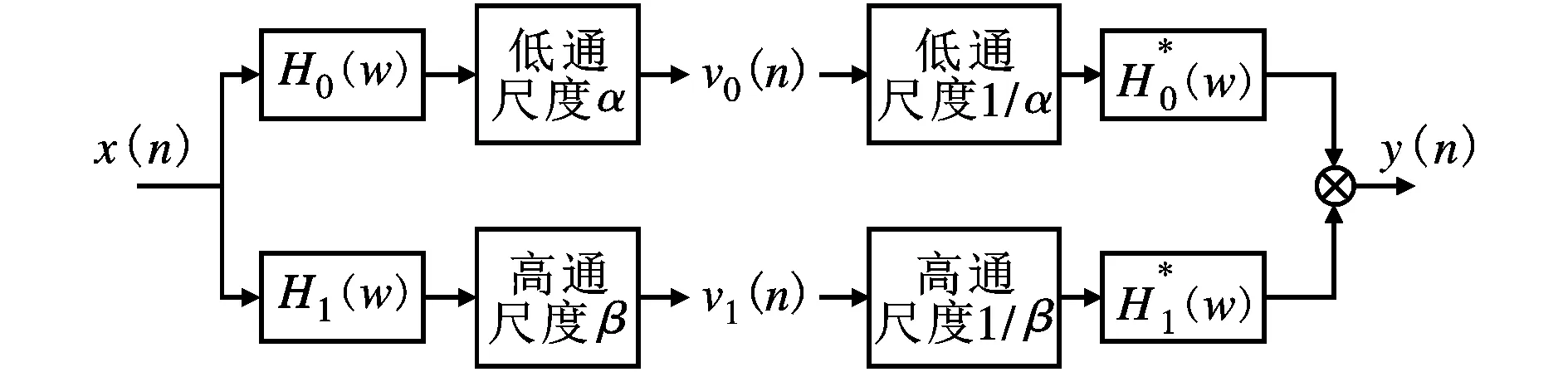
(a)滤波分解　　　(b)合成滤波器组图1　两通道滤波器组

1.2　共振分量分离

给定一个观察信号x,它由x1和x2这2个信号线性迭加而得,x1主要包括持续振荡的高共振分量,x2主要包括瞬态冲击的低共振分量,利用形态分量分析将信号中共振属性不同的分量分离开来,并且分离开来的两部分的耦合程度越小越好。假定信号x1和x2可分别用基函数库S1和S2(二者具有低的相关性,由TQWT方法获得)的稀疏表示,设定一个最小目标函数

λ1‖W1‖1+λ2‖W2‖1

(2)

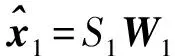
1.3　TQWT方法参数选择与影响

RSSD方法中采用Q来定义共振属性,不同Q的小波波形振荡次数不同。品质因子Q越大表征的共振属性越高,时域波形振荡次数越多,频率响应的分辨率越高,相邻两子带的重叠度越低,因此Q值的选择很大程度地影响高低共振分量的相关性(耦合程度)。文献[7]给出了品质因子Q1与Q2的相关性分析及表达式

(3)

由式(3)可以看出,Q1大于Q2,二者相差越大则相关性越低。若Q2=1,增大Q1可以降低相关性,并提高分辨率,但是品质因子太高,其小波基函数可能无法匹配高共振信号的振荡特性,会产生奇异信号,降低RSSD方法的准确性与可靠性。因此,只有合理地选择品质因子Q1与Q2才能获得较好的分解效果,使不同分量的相关性较低,获得所需信号成分。

实践应用中,冗余因子r一般在3～4之间取值。分解级数J决定了小波基函数库构建的元素数量,它影响着每一层子带中心频率大小与带宽大小。随着分解级数的增加,各级子带的中心频率与带宽越来越小,J与Q、r的关系为

(4)

式中:N为信号长度。Q越大,覆盖相同频率范围所需要匹配的分解级数越大。在实际应用中,参数J的选择需要具体分析研究对象的故障信息,以确保子带频率分布覆盖振动信号各成分的共振频带,有子带的中心频率与需要提取的分解成分相近。

2　品质因子优化与子带重构

2.1　品质因子优化

在选择品质因子时,传统的RSSD方法一般人为指定Q值,通常选择Q1=1,Q2=3～9之间的整数,具有一定的随机性,获得的分解效果不稳定。依据TQWT原理可知,如果想将携带故障信息的信号分解到特定共振属性的分量中,需要构建与故障信号振荡特征相匹配、相近的小波基函数库,也就是选择合适的品质因子。

峭度指标Kv可用来检验信号偏离正态分布的程度,其计算方法为

(5)

式中:ux为信号x的均值。当机械设备正常工作时,振动幅值呈正态分布,Kv≈3,当设备发生退化偏离正常状态时,Kv的绝对值会随着退化的程度相应增大。对于冲击类故障,与其他指标相比峭度指标的敏感性与稳定性均较好,一般谐波信号峭度小于3,而故障冲击信号峭度要比3大得多。因此,本文以信号分解后的低共振分量的峭度作为优化目标函数,采用遗传算法对不同的高低品质因子组合进行优化选择,以期获得分解效果较好的Q1和Q2,进而有效地进行特征提取与故障分析。

设置品质因子变化精度为0.01,采用十进制编码,设定初始种群规模为50,遗传代数为200,遗传概率为0.1,交叉概率为0.7,变异概率为0.02。遗传算法的具体步骤可参考文献[11]。根据遗传算法获得的品质因子组合,理论上所对应的低共振分量的峭度最大,所含故障信息最多,该分量能够比较全面地表征冲击成分。

2.2　子带重构

在背景噪声较强的工作环境中,滚动轴承故障信号经RSSD方法分解所得的高低共振分量由于噪声干扰导致耦合程度较大,低共振分量中冲击成分不明显,因此还可以考虑针对低共振分量进行子带重构,进一步凸显滚动轴承故障特征。张顶成等对RSSD方法得到的低共振分量进行品质因子可调小波重构,并结合峭度分析筛选出最佳分析分量,有效提取轴承故障信号中的冲击成分[12],但该方法在重构时只依据品质因子的滤波特性从高频到低频部分进行累加重构,并不考虑各频带关系及其在信号能量中所占的比重,从而将多个子带上的噪声引入到重构信号中。本文提出根据RSSD方法分解所得各子带能量在信号总能量中的比重动态选择子带进行信号重构,其具体过程如下。

步骤1利用TQWT方法对信号进行分解,分别计算L+1个子带信号能量Ej及其在总量中的百分比ej,其计算方法为

(6)

式中:Wji为第j层第i个小波系数;Nj为第j层小波系数长度。

步骤2当子带能量百分比大于子带平均能量1.5倍以上,即认为是能量比占优子带,即

ej≥1.5/(L+1)×100%

(7)

步骤3将选出的能量占优子带分别重构并进行线性迭加,合并成新的低共振分量。

3　诊断流程

RSSD方法根据信号成分和共振属性不同,将信号分解为具有2种不同Q的分量,即高共振分量和低共振分量,而不是将信号按频带进行分解划分。小波分析具有局部优化和多分辨的特性,从频域角度对信号进行多尺度展开,对于滚动轴承早期的微弱故障,将共振稀疏分解法与小波分析技术相结合,可以从信号共振属性和局部时频特性分析两方面形成互补,从而对故障信号进行深层次挖掘。具体实现步骤如下:

步骤1通过实验获取滚动轴承故障振动原始信号,按照2.1节所述的低共振分量的峭度最大原则采用遗传算法对品质因子参数组合进行优化选择,利用RSSD方法对信号进行分解;

步骤2根据2.2节所述方法对步骤1分解所得到的低共振分量进行子带选择与重构;

步骤3对重构的新的低共振分量进行小波多尺度分解,结合希尔伯特解调方法提取信号包络谱,获取轴承故障特征。

4　诊断实例

4.1　滚动轴承故障实验

轴承故障实验台由驱动电机、皮带轮、转动轴、轴承座、支架、加载电机、调速加载系统等部件组成。实验台工作过程中的转速信号由一个布置于联轴器处的非接触式测速仪测取,轴承振动信号通过2个布置于轴承座径向平面水平和垂直方向的振动加速度传感器测取。

实验所用的滚动轴承型号为6308型,轴承类型有正常、外圈剥落、内圈剥落和滚动体剥落4种。外圈剥落为点状损伤,约7 mm2,位于滚道中间(深约0.2 mm);内圈剥落为点状损伤,约3.6 mm2,位于滚道中间(深约0.1 mm);滚动体剥落为点状损伤,约1 mm2。实验中轴的转速为1 620 rad/min,转频fr=27 Hz,采样频率为20 kHz,采样点数为8 192,由式(1)可算出内圈故障特征频率fi=132 Hz,外圈故障特征频率fo=82 Hz,滚动体故障特征频率fb=55 Hz。因为外圈损伤较为明显,且传递路径较短,对其诊断较容易,所以本次诊断实例主要针对具有微弱故障并且传递路径更为复杂的内圈故障和滚动体故障进行诊断。

4.2　内圈故障诊断

图2给出了轴承内圈故障振动信号,由图2a可以看出,冲击间隔不均匀的故障冲击成分,由于故障比较微弱,并且受到环境噪声及信号能量衰减的影响,大部分冲击成分被淹没在噪声当中。采用希尔伯特变换对其进行包络解调分析,由图2b所示,在159 Hz(fi+fr)、237 Hz(2fi-fr)及502 Hz(4fi-fr)处存在明显的峰值,这是内圈故障信号受到转频的调制影响产生的结果,但是无法直接提取出明显的内圈故障特征频率。

(a)时域波形

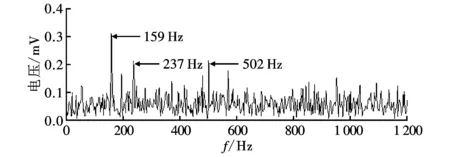
(b)包络谱图2　内圈故障振动信号

按2.2节所述诊断流程对滚动轴承内圈故障振动信号进行分析,首先利用RSSD方法对信号进行分解,根据信号采样频率及频带覆盖基本理论,结合以低共振分量的峭度最大为目标函数的遗传优化算法结果,确定Q1=3.75,Q2=1.06,r1=r2=3.5,L1=35,L2=15。信号分解后的结果如图3所示。图3a为振动信号的高共振分量,主要包含谐波成分;图3b为振动信号的低共振分量,信号中冲击成分相对明显,主要包含瞬态冲击成分。

(a)高共振分量

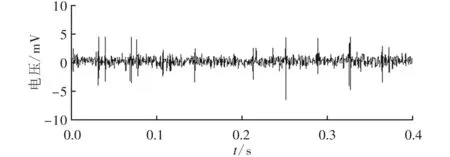
(b)低共振分量图3　内圈故障振动信号RSSD结果

图4给出了低共振分量的子带能量分布图,子带2、5、6、7、16能量较大,包含故障冲击信息较多,满足式(7)所规定的子带选择条件,因此选择这些子带进行低共振分量主子带信号重构。

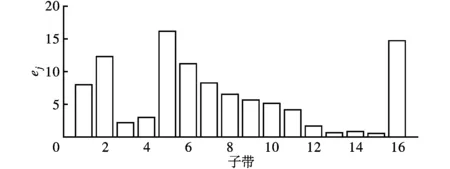
图4　低共振分量的子带能量分布

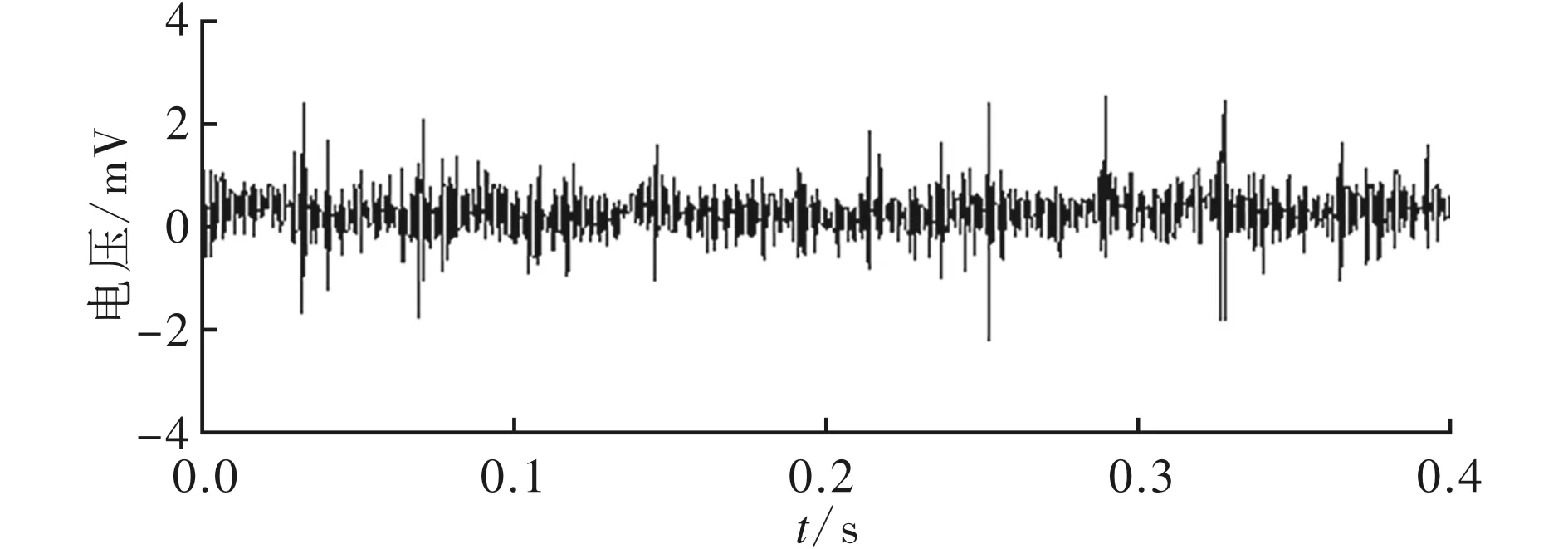
(a)时域波形

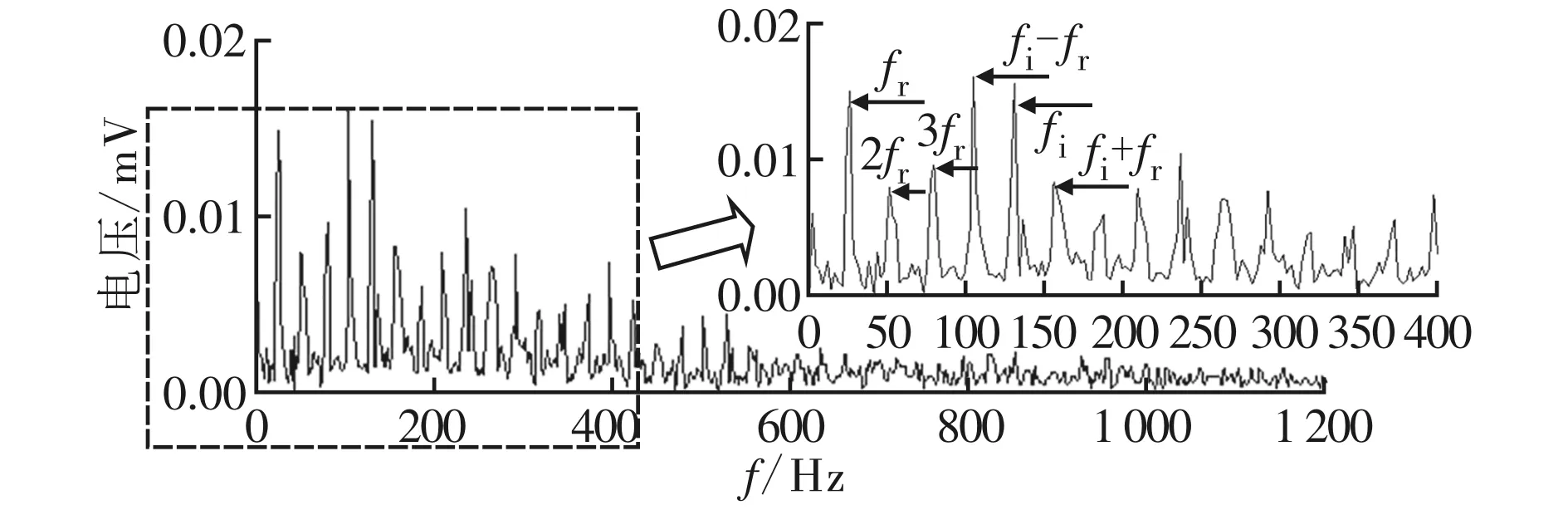
(b)小波变换的第1层细节信号包络谱图5　低共振分量主子带重构信号

图5a为低共振分量主子带重构信号,重构信号的冲击特性更加明显。为了对其局部时频特性进一步分析,采用db10小波对重构信号进行6层分解,图5b为第1层细节信号的包络谱及其低频细节放大部分,从图5中能清晰观察到内圈故障特征频率fi、转频及其倍频(fr、2fr和3fr)、内圈故障特征频率与转频的调制关系频率(fi±fr)。这些频率成分与滚动轴承内圈出现故障的特征相符合,说明产生了内圈故障。

为了与普通的共振稀疏分解特征提取方法对比,同时按一般模式直接分析低共振分量,图6给出了RSSD方法分解后低共振分量的包络谱。内圈故障特征频率fi及其与转频的调制边频(fi-fr、2fi-fr)都能观察到,但幅值都不占优。通过与图7结果对比分析可以发现,基于低共振分量主子带重构分析与小波变换相结合的方法可以对故障信息进行深层次挖掘,更加凸显故障特征。

图6　一般RSSD方法分析的低共振分量包络谱

4.3　滚动体故障诊断分析

图7给出了滚动轴承的滚动体故障振动信号,由图7a可以观察到间隔不均匀的故障冲击成分,但由于故障比较微弱,大部分冲击成分被淹没在噪声当中。同样采用希尔伯特变换对其进行包络解调分析,如图7b所示,在181、195、327和535 Hz处存在明显的峰值,但是难以观察到滚动体故障特征频率,原因在于滚动体出现故障时在损伤部位接触的时间间隔及位置不固定,信号传递路径更加复杂,易受到环境噪声及信号能量衰减的影响。

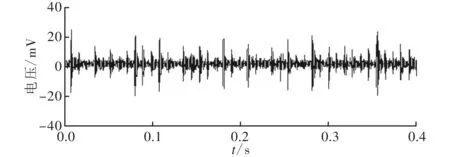
(a)时域波形

(b)包络谱图7　滚动体故障振动信号

同轴承内圈故障诊断类似,首先利用RSSD方法对信号进行分解,同样采用基于遗传算法的品质因子优化方法,并根据采样频率大小及频率覆盖原则,确定Q1=4.92,Q2=1.13,r1=r2=3.5,L1=40,L2=15。信号分解后所得的高、低共振分量如图8所示。

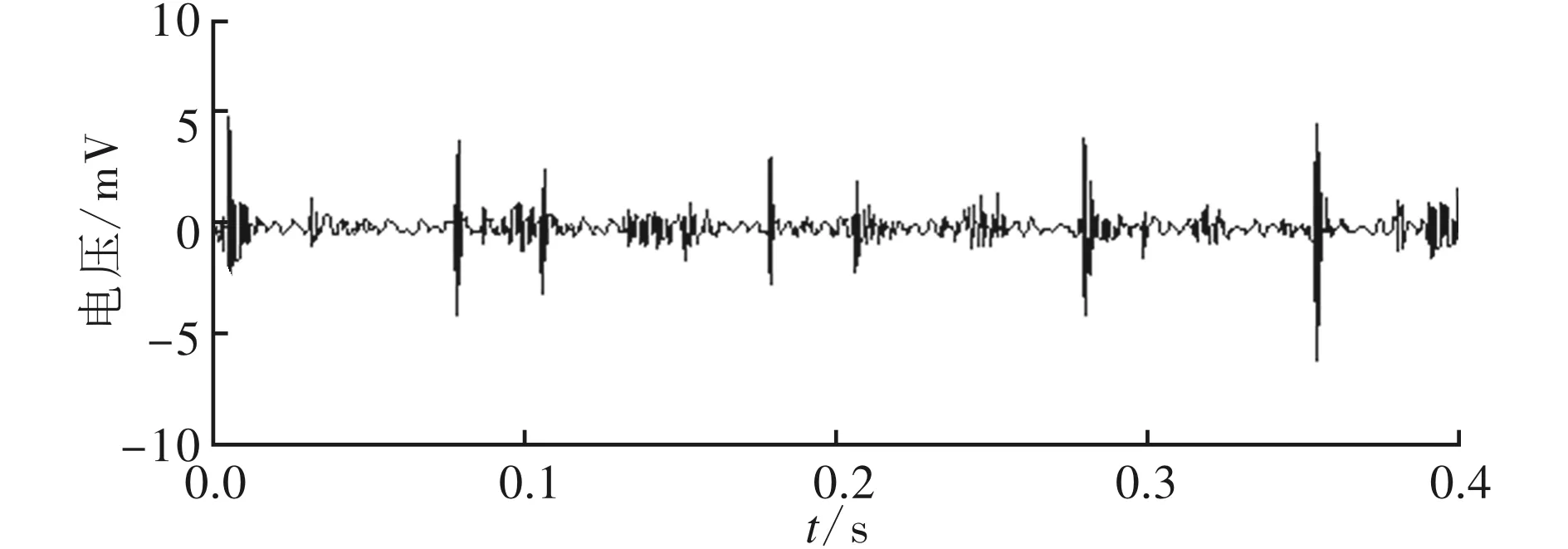
(a)高共振分量

(b)低共振分量图8　滚动体故障RSSD方法分析结果

图9给出了低共振分量的子带能量分布图,子带1、2、16能量较大,满足式(7)所规定的子带选择条件,因此将这些子带进行低共振分量主子带信号重构。

图9　低共振分量的子带能量分布

图10a为低共振分量主子带重构信号,可以看出冲击成分更加明显。同样采用db10小波对其进行6层分解,图10b为第1层细节信号的包络谱,能清晰观察到故障特征频率双倍频(2fb、4fb、6fb),这些特征符合滚动轴承滚动体故障特征,说明出现了滚动体故障。

图11给出了按一般模式直接分析RSSD方法分解后低共振分量的包络谱。可以观察到181、195(2fb+fr)、327(6fb)和535 Hz,除195 Hz和327 Hz与故障频率有一定关系外,其他频率均与故障无关。通过与图11结果对比分析,可以发现基于低共振分量主子带重构分析与小波变换相结合的方法,故障特征提取的效果更佳。

由上面滚动轴承故障诊断实例分析可以发现,基于RSSD方法和小波变换的滚动轴承故障诊断技术在故障特征凸显方面效果更加明显,能够有效提取故障特征,使得滚动轴承故障特征观察更加清晰和准确。该方法具有RSSD方法成分分离的优势,利用了小波多分辨特性,在滚动轴承早期微弱故障诊断中有良好的应用效果。

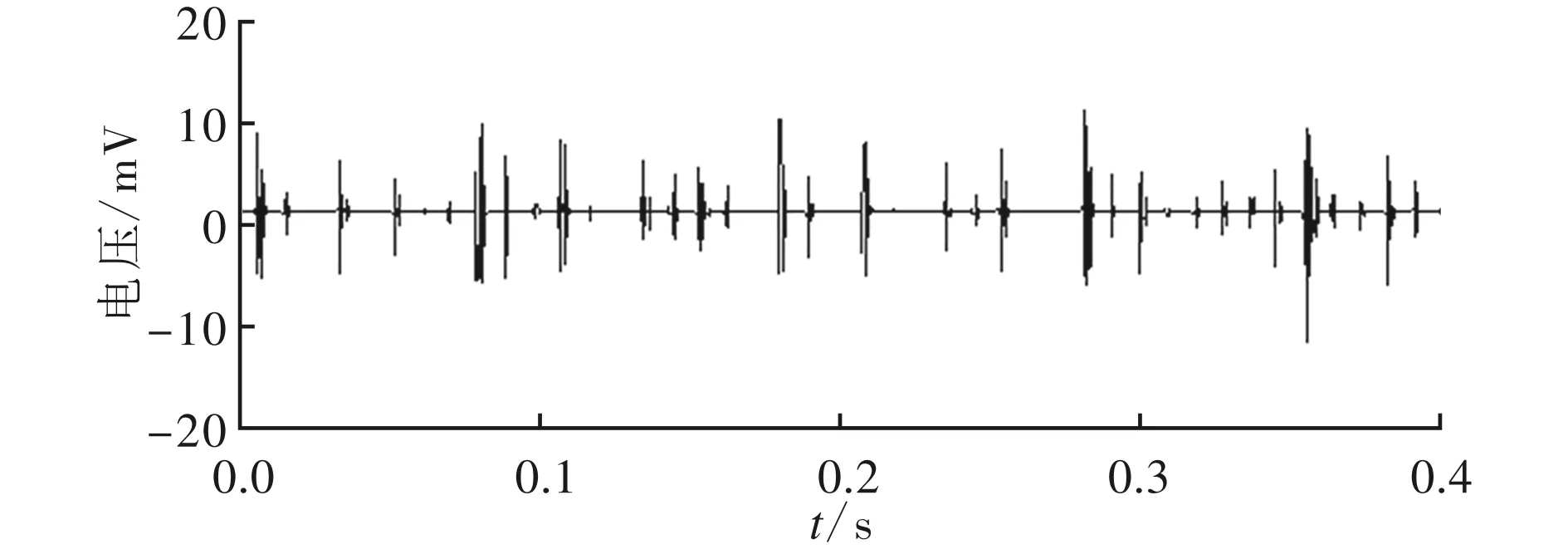
(a)时域波形

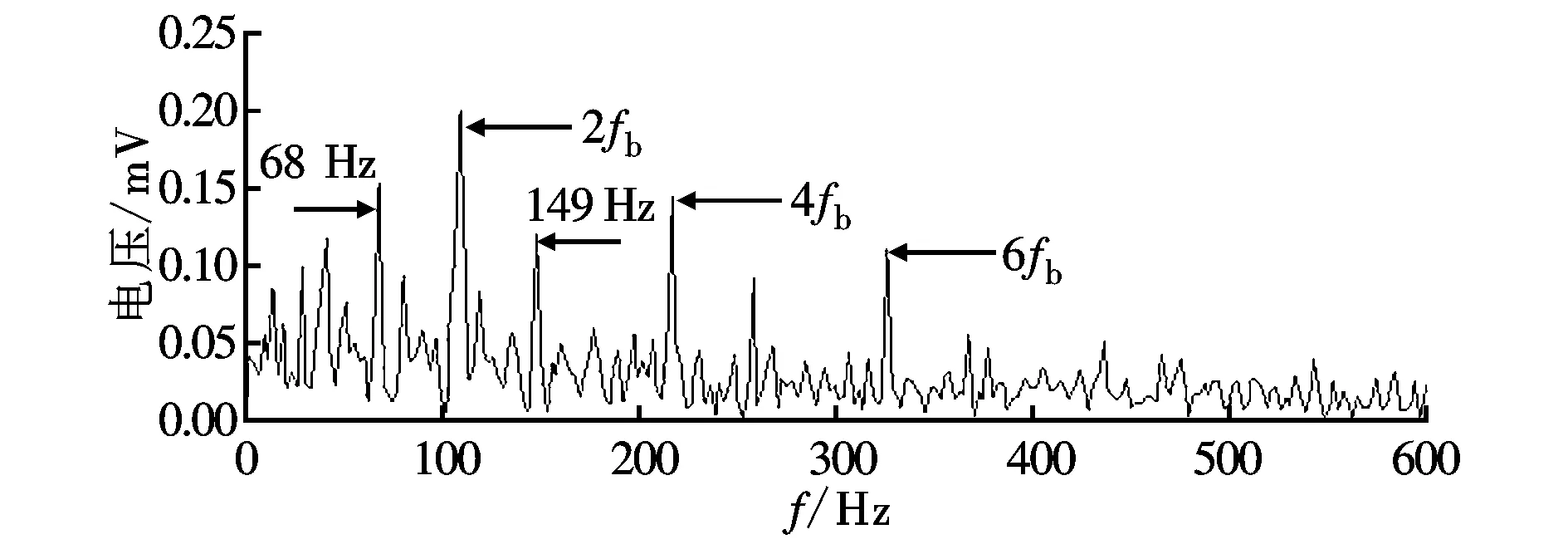
(b)小波变换的第1层细节信号包络谱图10　低共振分量主子带重构信号

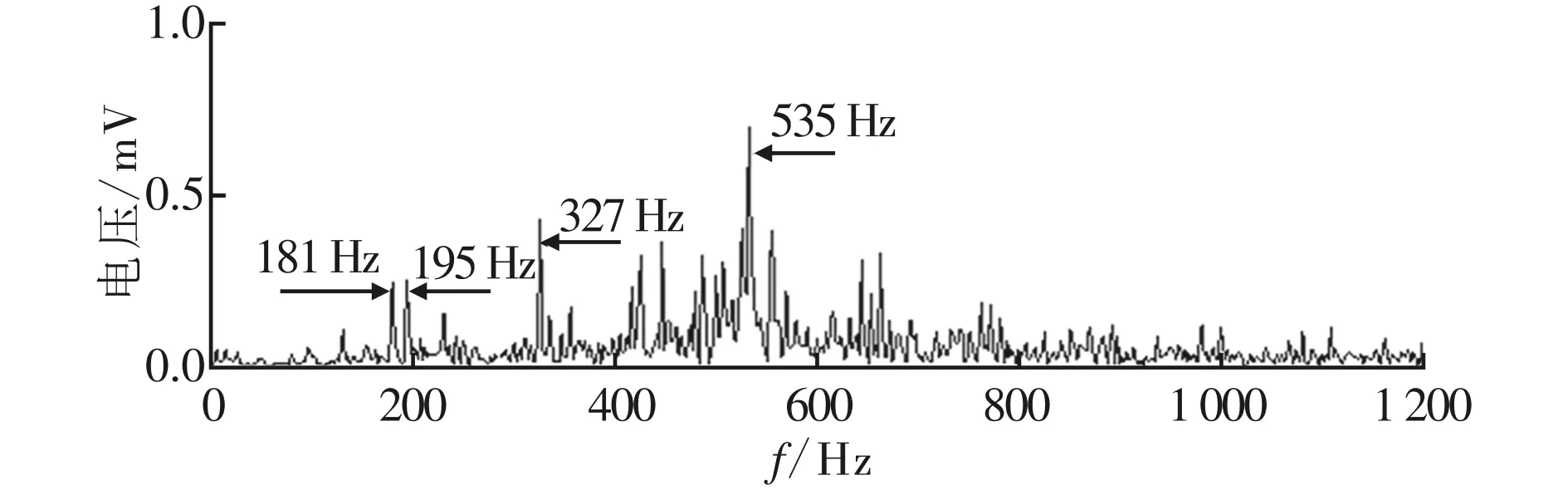
图11　一般RSSD方法分析的低共振分量包络谱

5　结　论

本文提出了一种融合遗传算法品质因子参数优化、子带重构RSSD方法和小波变换的故障诊断方法,通过对滚动轴承早期故障诊断分析,得到如下结论:

(1)在滚动轴承早期出现故障时信号能量较微弱,易受到环境噪声及信号能量衰减的影响,信号冲击特性表现不明显,直接利用RSSD方法低共振分量进行信号分析时,并不能提取到明显的故障特征频率。结合品质因子参数优化和子带重构的RSSD方法,可有效地增强轴承早期故障信号冲击特性,凸显微弱故障特征。

(2)RSSD方法根据信号共振属性不同,将复杂信号分解成由持续振荡成分组成的高共振分量和由瞬态冲击成分组成的低共振分量;小波分析具有局部优化和多分辨的特性,从频域角度对信号进行多尺度展开。将共振稀疏分解法与小波分析技术相结合,可以从信号共振属性和局部时频特性分析两方面形成互补,从而对故障信息进行深层次挖掘。

(3)通过2种不同轴承故障诊断实例说明,与已有的RSSD方法相比,融合遗传算法品质因子参数优化、子带重构的RSSD方法和小波变换相结合的滚动轴承故障诊断方法取得了更好的结果,实现了滚动轴承早期出现故障的准确诊断。

参考文献:

[1]何正嘉, 陈进, 王太勇, 等. 机械故障诊断理论及应用 [M]. 北京: 高等教育出版社, 2010: 234-239.

[2]严如强, 钱宇宁, 胡世杰, 等. 基于小波域平稳子空间分析的风力发电机齿轮箱故障诊断 [J]. 机械工程学报, 2014, 50(11): 9-16.

YAN Ruqiang, QIAN Yuning, HU Shijie, et al. Fault diagnosis of wind turbine gearbox based on wavelet domain stationary subspace analysis [J]. Journal of Mechanical Engineering, 2014, 50(11): 9-16.

[3]郑近德, 程军圣. 改进的希尔伯特-黄变换及其在滚动轴承故障诊断中的应用 [J]. 机械工程学报, 2015, 51(1): 138-145.

ZHENG Jinde, CHEN Junsheng. Improved Hilbert Huang transform and its application in fault diagnosis of rolling bearings [J]. Journal of Mechanical Engineering, 2015, 51(1): 138-145.

[4]WANG Yanxue, HE Zhengjia, ZI Yanyang. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis [J]. ASME Journal of Vibration and Acoustics, 2010, 132(2): 613-624.

[5]CHEN Baojia, HE Zhengjia, CHEN Xuefeng, et al. A demodulating approach based on local mean decomposition and its applications in mechanical fault diagnosis [J]. Measurement Science & Technology, 2011, 22(5): 05574.

[6]向家伟, 崔向欢, 王衍学, 等. 轴承故障诊断的最优化随机共振方法分析 [J]. 农业工程学报, 2014, 50(12): 50-55.

XIANG Jiawei, CUI Xianghuan, WANG Yanxue, et al. Optimal random resonance analysis of bearing fault diagnosis [J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 50(12): 50-55.

[7]SELESNICK I W. Resonance-based signal decomposition: A new sparsity-enabled signal analysis method [J]. Signal Processing, 2011, 91(12): 2793-2809.

[8]黄文涛, 付强, 窦宏印. 基于自适应优化品质因子的共振稀疏分解方法及其在行星齿轮箱复合故障诊断中的应用 [J]. 机械工程学报, 2016, 52(15): 44-51.

HUANG Wentao, FU Qiang, DOU Hongyin. Resonance sparsity decomposition method based on adaptive optimization quality factor and its application in complex fault diagnosis of planetary gear box [J]. Journal of Mechanical Engineering, 2016, 52(15): 44-51.

[9]张文义, 于德介, 陈向民. 基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法 [J]. 中国电机工程学报, 2013, 33(20): 111-118.

ZHANG Wenyi, YU Dejie, CHEN Xiangmin. Fault diagnosis method of bearing based on signal resonance sparse decomposition and Energy Operator Demodulation [J]. Proceedings of the CSEE, 2013, 33(20): 111-118.

[10] ILKER B SELESNICK I W. Frequency-domain design of overcomplete rational-dilation wavelet transforms [J]. IEEE Transactions on Signal Processing, 2009, 57(8): 2957-2972.

[11] 李星, 于德介, 张顶成. 基于最优品质因子信号共振稀疏分解的滚动轴承故障诊断 [J]. 振动工程学报, 2015, 28(6): 998-1005.

LI Xing, YU Dejie, ZHANG Dingcheng. Fault diagnosis of rolling bearing based on optimal quality factor signal resonance sparsity decomposition [J]. Journal of Vibration Engineering, 2015, 28(6): 998-1005.

[12] 张顶成, 于德介, 李星. 滚动轴承故障诊断的品质因子可调小波重构方法 [J]. 航空动力学报, 2015, 30(12): 3051-3057.

ZHANG Dingcheng, YU Dejie, LI Xing. Quality factor adjustable wavelet reconstruction method for rolling bearing fault diagnosis [J]. Journal of Aerospace Power, 2015, 30(12): 3051-3057.