考虑波动趋势和相关性的多风电场模拟出力数据生成方法
郭璋, 司刚全, 黄越辉, 李湃
(1.西安交通大学电气工程学院, 710049, 西安; 2.中国电力科学研究院有限公司, 100192, 北京)
中国的风能资源分布较为集中,因而决定了风电开发过程中具有规模化、连片式发展的特点[1]。尤其在风资源丰富的地区常常存在多个地理位置相近的风电场,且由于气象因素,这些风电场间的出力通常会具有明显的相关性。多风电场的相关性,以及风力发电的随机性、波动性、间歇性等不确定性特点对电力系统的安全稳定运行具有极大的挑战[2-3]。因此,综合风电场出力的波动特性,考虑多风电场出力的互相关特性,建立多风电场的模拟出力序列模型,对研究大规模风电接入系统,以及对于电网规划与电力系统的调度运行具有重要意义[4-8]。
目前,国内外对于单个风电场出力数据生成的方法已经进行了大量的研究[9-13]。文献[9]根据ARMA模型对风电场出力序列进行建模;文献[10]依据风电装机容量的变化对历史出力进行调整,以应用于电力系统分析;文献[11]利用马尔科夫链蒙特卡洛方法对风电出力序列进行建模;文献[12]将风电场历史出力序列划分为多个波动过程,按月抽样风电波动类别和波动统计参数,模拟风电场出力序列;文献[13]将风电场出力序列划分为多个风过程,根据概率统计结果模拟生成风电场出力序列。
对于多风电场出力数据的生成,还要考虑到多风电场出力之间的互相关性[14-17]。文献[14]考虑时延关系得到多风电场的风速序列;文献[15]以各个风电场的历史风速概率密度、互相关系数等为约束条件,得到风速序列;文献[16]考虑了多变量之间的互相关性来模拟风电出力序列;文献[17]根据风速的相关性建立了统一出力模型。目前,国内外还有很多学者运用Copula函数研究多风电场出力的相关性[18-21]。文献[18]基于特定的Copula函数生成了多风电场模拟出力序列;文献[19]提出了基于混合Copula函数的风电功率相关性分析方法;文献[20]应用Copula函数对欧洲风电场数据进行了实例分析。
目前,已有研究方法大多只满足出力的整体统计特性和整体互相关性,多针对出力序列整体数据进行分析,易忽略局部相关特性,对于出力的局部相关性和出力波动趋势都表现不足。因此,在深入分析出力波动特性的基础上,本文提出一种考虑多风电场出力波动趋势和相关性的模拟出力序列建模方法,在考虑风电场自身出力趋势的同时兼顾了多风电场的互相关特性,为多风电场波动特性分析、电力系统随机生产模拟、电力系统风电接纳能力评估等奠定了基础。
1 风电场波动过程分析及定量描述
基于现有风电场出力序列分析和建模研究基础,风电场整体波动特性可以用去除扰动后的趋势序列进行描述[12-13],并用高斯函数定量表达波动过程[12]。通过小波分解算法进行滤波分离,可将风电出力序列分解为低频出力和高频出力两部分。高频出力可看作是随机出力扰动,而低频出力则为风电的趋势出力,反映整体的波动趋势特性。
将出力序列从一个局部极小值,间隔一个局部极大值,到达另一个局部极小值的过程定义为一个风电出力波动过程[12],则风电趋势序列可用若干个波动过程连接构成的时间序列进行描述。波动过程的数学模型如下
(1)
式中:Wi{Pl}为第i个波动过程;{P}为风电场出力序列;{Pmin}为局部极小值序列;{Pmax}为局部极大值序列。该波动过程长度为m-n+1,起点为Pn,终点为Pm。
波动过程可近似用高斯函数进行拟合,以对波动过程的定量描述[12],拟合公式如下
(2)
式中:ai、bi、ci为第i个波动对应的无量钢波动拟合参数,ai为极值大小参数,bi为极值位置参数,ci为变化趋势参数;fi(·)为计算得到的各时刻出力值;x为波动过程中各时刻与局部极大值对应时刻的差值,当x=0时,fi(0)为第i个波动过程的局部极大值。
除波峰小于ε(ε=0.05)的波动过程识别为低出力波动外,其他波动识别为有效波动。分别统计低出力波动的持续时间l和有效波动的波动持续时间d。
将有效波动的拟合参数a、b、c和波动持续时间d作为多维随机变量,统计多维概率分布,其中a和c反应了波动的形状特征,b和d反应了波动的时间位置特征。实际应用中,a、b、c、d这4个参数的相关性较弱,可以直接作为独立变量进行处理。
对于低出力波动和有效波动的转换过程,可以通过马尔科夫链模拟计算波动转移矩阵[13],计算方式为
(3)

2 多风电场波动特性相关性分析
在前文所述的现有风电场出力序列定量表达波动过程的基础上,本文从波动过程参数具有相关性这一新的角度,深入分析了出力序列之间的相关性,给出了从整体趋势特性分析出力相关性以及模拟出力序列构建的方法,并由此生成了具有相关性的多风电场模拟序列。
2.1 Copula相关性分析
Copula理论可以将多维联合概率函数表示为各自的边缘分布的一种连接,并用Copula函数进行描述。
Copula函数定义为C(u1,u2,…,uN),使得随机变量X1,X2,…,XN的F(x1,x2,…,xN)联合分布函数与各自的边缘分布函数FXi(xi)满足
F(x1,x2,…,xN)=
C(FX1(x1),FX2(x2),…,FXN(xN))
(4)

2.2 月份类别划分
风电出力具有季节性变化特征,各月份波动特性具有一定差异,实际中某些月份的出力波动特性相似,可将波动特性相似的年度月份进行分类聚合。这样可以有更多的波动过程数据参与分析,能够更好地反映模型特点。
月份类别划分的具体方法为,将每个月的极值参数a的概率密度函数按等间隔取值,得到12组相同长度的序列。通过k-均值聚类识别,将一年中12个月份分类为高、中、低出力3类。在统计有效波动的波动拟合参数的概率分布时,分别统计这3类月份的数据。本文在具体算例分析中,使用中出力月份的数据进行分析模拟。
2.3 波动过程的相关性分析
通常地理位置接近,天气因素相近的风电场的出力序列会具有显著的相关性,具体表现为各个波动过程的相似特性。图1为两风电场的趋势序列,其出力趋势以及波动划分后的各个波动过程都具有很强的相似性。如果直接对多个风电场对应的波动过程的序列值进行相关性分析,则因各个波动过程的持续时间和起始时间不相同等因素,很难得到有效的分析结果。

图1 两风电场趋势序列和波动过程划分
观察图1可以发现,两个风电场时间相近的波动过程具有明显的相似性,尤其在形状特性上。本文考虑将各风电场的波动过程进行配对后,对有效波动的拟合参数进行相关性分析。首先,根据波动过程的峰值是否在另一波动过程的范围内,对多组波动过程进行配对;其次,统计有效波动的波动拟合参数a、b、c、d,对反应波动形状特征的参数a和c进行Copula相关性分析,计算对应的Norm-Copula模型。

(5)
(6)

大部分波动过程可直接实现一一对应。如图1在0~20 h范围内的两个风电场的两个波动过程,其波动峰值均处于对方波动过程内,则可将这两个波动过程进行配对。对于不能实现直接配对的主要有两种情形:一种情形为某一风电场中的两个时间接近的波动过程,同时对应于另一风电场中的一个波动过程,其实际为时间紧邻的两个波动过程的重合;另一种情形为某一风电场出力波动值过小被直接忽略。在具体计算中,可只使用配对成功的波动过程进行统计分析,将其他情形忽略。因为已经对全年数据进行了分月聚合分类,所以具有足够多的匹配成功波动过程进行波动拟合参数的相关性分析。
对波动过程进行相关性分析后,可得到多个风电场有效波动的拟合参数a、b、c、d的概率统计结果,以及参数a和c对应的两个Copula函数模型。对于反应波动时间位置特征的参数b和d,不同风电场之间的差异可以理解为各自的时移特性,主要反应了不同风电场受同一天气过程影响的时间响应差异,其相关性相对不明显,且在考虑相关性的抽样重构过程中,b和d的取值受到一定约束。参数b的数值较小,影响程度低,可直接使用风电场各自的统计结果随机抽样。实际抽样过程中,为了保持配对状态的一致,多个风电场的参数d需保持近似一致。
3 构建模拟出力序列
3.1 生成趋势序列
根据两类波动的参数a、b、c、d、l的概率分布,两类波动的转移矩阵PT,以及已配对的有效波动对应参数a和c的Copula函数模型,可以生成具有相关性的多风电场的模拟趋势序列。
以两个风电场的情形为例,序贯抽样建立多风电场模拟趋势序列的过程如下。
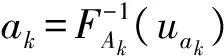
(3)根据有效波动的拟合参数a、b、c、d和低出力波动的参数l,依次逐点计算出各自出力值,即得到两个风电场对应的波动过程的出力值。
(4)连续抽样多个波动过程并顺序连接,当序列长度满足需求时,停止抽样。滤波后得到光滑连接的模拟趋势序列。
3.2 重构出力序列
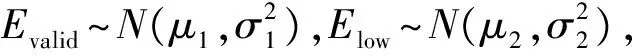
3.3 建模流程
综上,考虑多风电场出力波动趋势和相关性的模拟出力序列建模方法流程如图2所示。

图2 多风电场模拟出力序列建模流程
4 算例分析
取中国西北某省两邻近风电场一年的历史数据进行分析建模,通过月份分类后,分成高、中、低出力3类月份数据。本文以中出力月份为例进行建模分析,模拟生成一个月份长度的完整出力数据,得到与历史序列特征相近的模拟趋势序列和模拟出力序列,并能保持多风电场之间模拟序列的相关性。
4.1 波动特征提取及相关性分析
首先对两个风电场的历史出力序列进行滤波,得到两组历史趋势序列,然后对序列进行波动划分,两风电场的历史出力序列和滤波后的历史趋势序列如图3和图4所示。

图3 两风电场历史出力序列对比

图4 滤波后两风电场历史趋势序列对比
使用聚类方法将一年中各月分为高、中、低出力月份3种情况,如表1所示,以中出力月份为例进行分析计算。

表1 自然月聚类结果
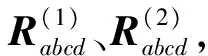



(a)极值大小参数

(b)极值位置参数
(c)变化趋势参数
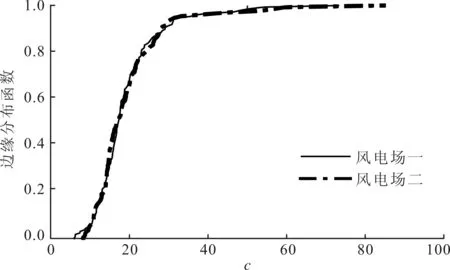
根据波动划分结果,对两风电场中出力月份的所有有效波动进行一一配对。根据配对结果进行两风电场对应的波动拟合参数的相关性分析,两风电场间a、b、c、d参数的相关性分别为0.93、0.55、0.8、0.51。其中反应波动形状特征的参数a和c的相关性显著,对其建立相应的Norm-Copula函数模型,在后续具体抽样建模过程中也主要体现a、c的相关性。

(d)波动持续时间图5 两风电场波动拟合参数的边缘分布函数
4.2 模拟出力序列建模
根据以上分析得到两风电场的各项统计参数,包括波动过程参数a、b、c、d、l,波动转移矩阵PT,参数a和c对应的Copula函数模型,建模得到具有两个具有相关性的模拟趋势序列,再根据随机出力统计参数μ1、μ2、σ1、σ2叠加随机出力,得到最终的模拟出力序列。
图6为两风电场的模拟趋势序列对比。从图中可以明显看出,模拟的风电场一和风电场二的出力趋势特性具有显著相关性,在保持各波动过程的主要参数具有特定相关性的同时,两风电场的模拟趋势序列的相关性也接近两风电场历史趋势序列的相关性水平。
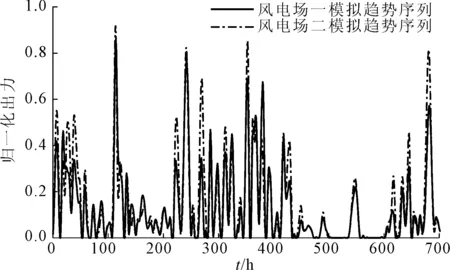
图6 两风电场模拟趋势序列对比
4.3 结果验证
算例主要从序列的概率密度函数(PDF)、15 min最大波动概率、相关性和波动拟合参数统计等几方面来评价本文建模方法,验证模型的有效性。
图7~图9分别为风电场一的历史出力序列和模拟出力序列、以及对应的概率密度函数(PDF)和15 min最大波动概率对比。从图7可以看出,历史出力序列和模拟出力序列具有相似的波动趋势结构。观察图8和图9中的序列波动概率可以发现,本文方法生成的模拟出力序列与历史出力序列具有一致的统计特性。以上结果证明本方法可以模拟生成具有所需的统计特性的出力序列。
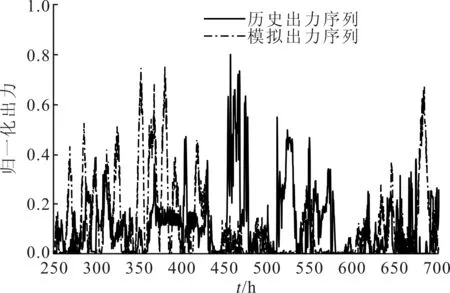
图7 风电场一历史出力序列和模拟出力序列的对比

图8 风电场一历史出力序列与模拟出力序列PDF的对比

图9 风电场一历史出力序列与模拟出力序列15 min最大波动概率的对比
表2是两风电场的序列之间的相关性对比,包括历史出力序列、历史趋势序列、模拟出力序列、模拟趋势序列。通过相关性对比,验证了两风电场模拟序列的相关性特性,与历史序列的相关性特性基本保持一致,表明本文方法可以保证生成的模拟序列满足需求的相关性特性。

表2 两风电场序列相关系数的对比
图10为风电场一历史出力序列与模拟出力的波动拟合参数的统计对比图。波动拟合参数的对比主要体现了生成的模拟数据对于风电场的波动趋势特性是否能保证有效复现。其他常见序列模拟方法中,对于趋势特性缺少关注,大多只能满足整体特性,而对于局部的相关性和参数特性则未能满足。从图10中可以看出,本文方法得到的模拟序列保持了趋势特性的一致和多风电场趋势的相关性。

(a)极值大小参数
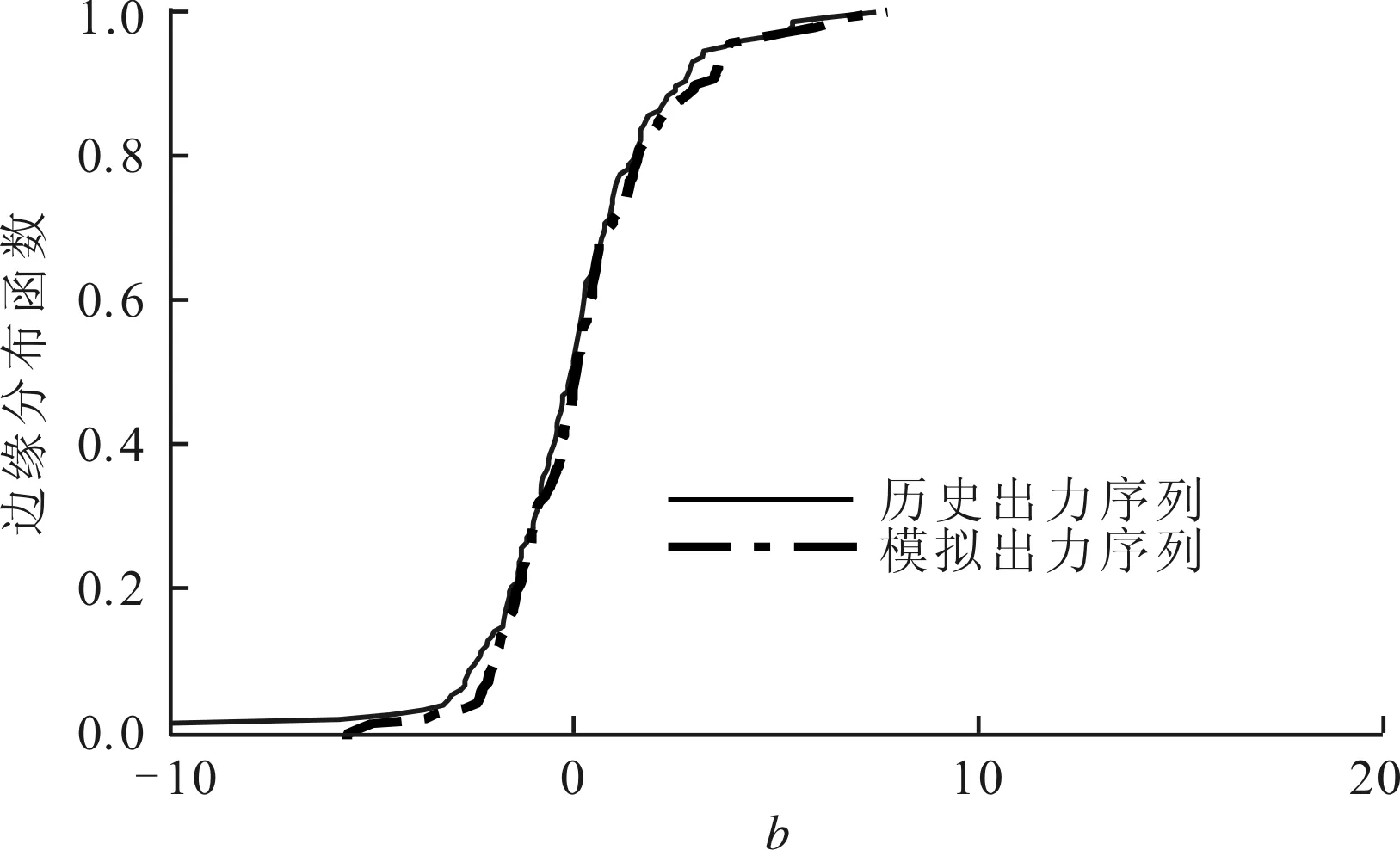
(b)极值位置参数

(c)变化趋势参数
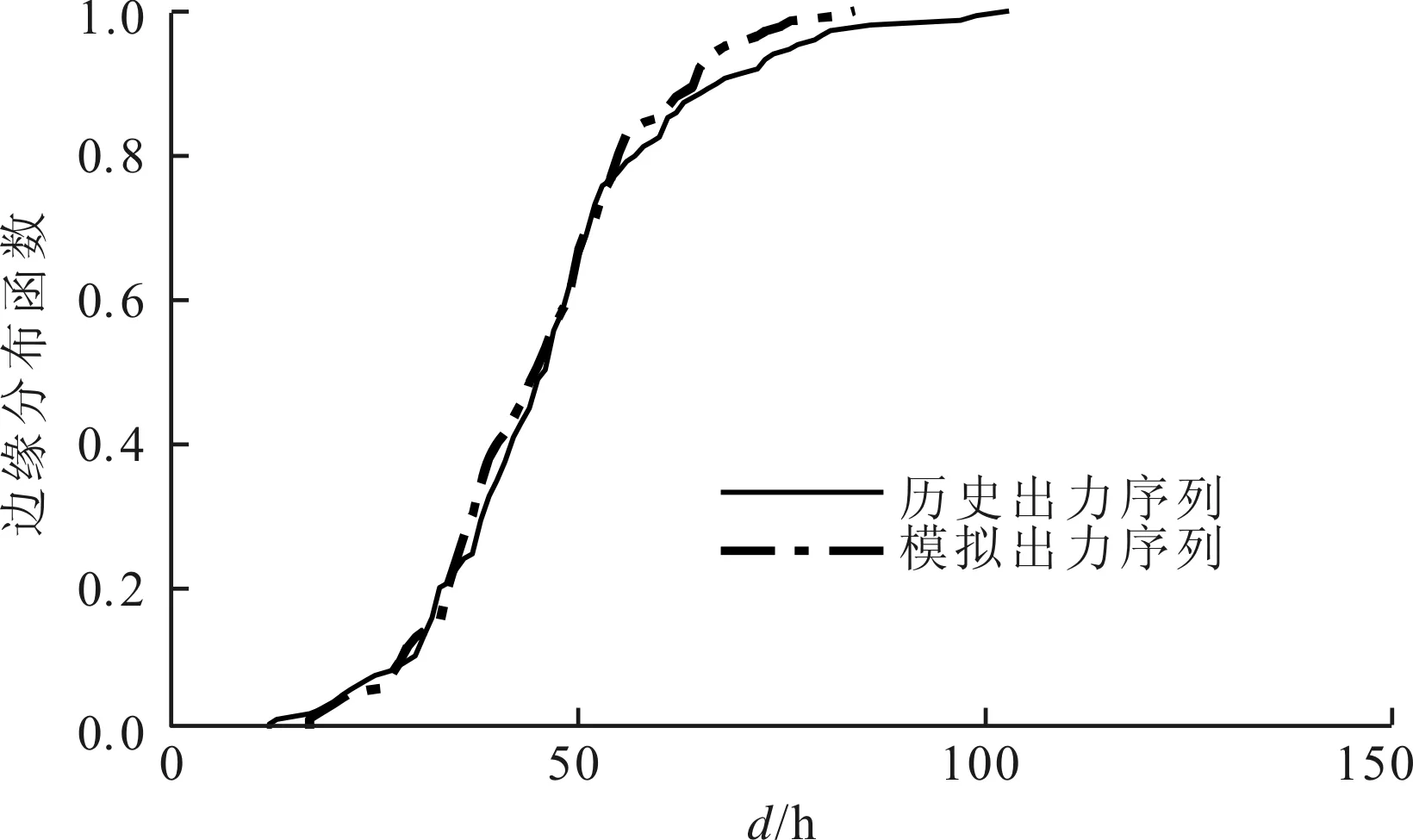
(d)波动持续时间图10 风电场一历史出力序列与模拟出力序列波动拟合参数特性对比
5 结 论
本文提出一种考虑多风电场出力波动趋势和相关性的模拟出力序列建模方法,可以建立具有相关性的多个风电场的模拟出力序列,并准确描述风电场出力序列的波动特性。在已有波动特性定量表达的基础上,本文深入分析了出力趋势的相关性特性,对具体的波动过程进行了配对处理,从波动过程参数具有相关性这一新的角度分析了出力序列之间的相关性,给出了从整体趋势特性分析出力相关性的方法,使得生成的模拟序列在趋势特性上能够保持统计特性一致的同时,还能保证多个风电场的相关性符合要求。下一步的研究工作中,一方面将继续完善出力趋势和高频波动的建模过程,另一方面将研究该模型在电力系统的仿真分析与计算中的应用,包括电力系统生产模拟、风电接纳能力评估等问题。
参考文献:
[1]尹明, 葛旭波, 王成山. 我国风电大规模开发相关问题探讨 [J]. 中国电力, 2010, 43(3): 59-62.
YIN Ming, GE Xubo, WANG Chengshan. Analysis of issues about China’s large-scale wind power development [J]. Electric Power, 2010, 43(3): 59-62.
[2]袁建党, 袁铁江, 晁勤, 等. 电力市场环境下大规模风电并网系统电源规划研究 [J]. 电力系统保护与控制, 2011, 39(5): 22-26.
新生事物的出现总不是一帆风顺的,人们在向未知领域探索的过程中,各种习惯势力、已有的学说与传统的观念,常常会严重束缚人们的思想,只有具备敢于冒险、敢于批判、敢于创新的开拓精神,才有可能冲破习惯势力的阻挠、传统观念的束缚,完善或修正原有的学说,开辟新领域,创造新天地。因此,科学家在追求真理,发现真理时,需要愈越重重障碍或阻隔[6]。他们既要有非凡的勇气与开拓精神,又要有对新发现、新发明的坚定信念,以及敢于坚持真理,为真理不屈不挠,奋不顾身的坚强斗志。科学家在追求真理时的矢志不渝是他们走向成功的基础。
YUAN Jiandang, YUAN Tiejiang, CHAO Qin, et al. Study of generation expansion planning of the power system incorporating large-scale wind power in the environment of electricity market [J]. Power System Protection and Control, 2011, 39(5): 22-26.
[3]余民, 杨旻宸, 蒋传文, 等. 风电并网后电力系统可靠性评估和备用优化研究 [J]. 电力系统保护与控制, 2012, 40(12): 100-104.
YU Min, YANG Minchen, JIANG Chuanwen, et al. Study on power system reliability and reserve optimization with wind power integration [J]. Power System Protection and Control, 2012, 40(12): 100-104.
[4]张宁, 周天睿, 段长刚, 等. 大规模风电场接入对电力系统调峰的影响 [J]. 电网技术, 2010(1): 152-158.
ZHANG Ning, ZHOU Tianrui, DUAN Changgang, et al. Impact of large-scale wind farm connecting with power grid on peak load regulation demand [J]. Power System Technology, 2010, 34(1): 152-158.
[5]邹斌, 李冬. 基于有效容量分布的含风电场电力系统随机生产模拟 [J]. 中国电机工程学报, 2012, 32(7): 23-31.
ZOU Bin, LI Dong. Power system probabilistic production simulation with wind generation based on available capacity distribution [J]. Proceedings of the CSEE, 2012, 32(7): 23-31.
[6]张宁, 康重庆, 陈治坪, 等. 基于序列运算的风电可信容量计算方法 [J]. 中国电机工程学报, 2011, 31(25): 1-9.
ZHANG Ning, KANG Chongqing, CHEN Zhiping, et al. Wind power credible capacity evaluation model based on sequence operation [J]. Proceedings of the CSEE, 2011, 31(25): 1-9.
[7]范荣奇, 陈金富, 段献忠, 等. 风速相关性对概率潮流计算的影响分析 [J]. 电力系统自动化, 2011, 35(4): 18-22.
FAN Rongqi, CHEN Jinfu, DUAN Xianzhong, et al. Impact of wind speed correlation on probabilistic load flow [J]. Automation of Electric Power Systems, 2011, 35(4): 18-22.
[8]李玉敦, 谢开贵, 胡博. 基于Copula函数的多维时序风速相依模型及其在可靠性评估中的应用 [J]. 电网技术, 2013, 37(3): 840-846.
LI Yudun, XIE Kaigui, HU Bo. A copula function-based dependent model for multivariate wind speed time series and its application in reliability assessment [J]. Power System Technology, 2013, 37(3): 840-846.
[9]CHEN Peiyuan. Stochastic modeling and analysis of power system with renewable generation [J]. BMC Genetics, 2010, 7(2): 1-14.
[10] 刘德伟, 黄越辉, 王伟胜, 等. 考虑调峰和电网输送约束的省级系统风电消纳能力分析 [J]. 电力系统自动化, 2011, 35(22): 77-81.
LIU Dewei, HUANG Yuehui, WANG Weisheng, et al. Analysis on provincial system available capability of accommodating wind power considering peak load dispatch and transmission constraints [J]. Automation of Electric Power Systems, 2011, 35(22): 77-81.
[11] PAPAEFTHYMIOU G, KLOCKL B. MCMC for wind power simulation [J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 234-240.
[12] 李驰, 刘纯, 黄越辉, 等. 基于波动特性的风电出力时间序列建模方法研究 [J]. 电网技术, 2015, 39(1): 208-214.
LI Chi, LIU Chun, HUANG Yuehui, et al. Study on the modeling method of wind power time series based on fluctuation characteristics [J]. Power System Technology, 2015, 39(1): 208-214.
[13] 刘纯, 吕振华, 黄越辉, 等. 长时间尺度风电出力时间序列建模新方法研究 [J]. 电力系统保护与控制, 2013, 41(1): 7-13.
LIU Chun, LÜ Zhenhua, HUANG Yuehui, et al. A new method to simulate wind power time series of large time scale [J]. Power System Protection and Control, 2013, 41(1): 7-13.
[14] XIE Kaigui, BILLINTON R. Considering wind speed correlation of WECS in reliability evaluation using the time-shifting technique [J]. Electric Power Systems Research, 2009, 79(4): 687-693.
[15] 王松岩, 于继来, 李海峰, 等. 考虑统计和互相关特性的多风电场风速数据模拟生成方法 [J]. 电力系统自动化, 2013, 37(6): 18-23.
WANG Songyan, YU Jilai, LI Haifeng, et al. A wind speed modeling method for multiple wind farms considering correlation and statistical characteristics [J]. Automation of Electric Power Systems, 2013, 37(6): 18-23.
[16] 罗钢, 石东源, 陈金富, 等. 风光发电功率时间序列模拟的MCMC方法 [J]. 电网技术, 2014, 38(2): 321-327.
LUO Gang, SHI Dongyuan, CHEN Jinfu, et al. A Markov chain Monte Carlo method for simulation of wind and solar power time series [J]. Power System Technology, 2014, 38(2): 321-327.
[17] LI Yan, ZHOU Ming, WANG Dawei, et al. Universal generating function based probabilistic production simulation approach considering wind speed correlation [J]. Energies, 2017, 10(11): 1786.
[18] PAPAEFTHYMIOU G, KUROWICKA D. Using copulas for modeling stochastic dependence in power system uncertainty analysis [J]. IEEE Transactions on Power Systems, 2009, 24(1): 40-49.
[19] 潘雄, 王莉莉, 徐玉琴, 等. 基于混合Copula函数的风电场出力建模方法 [J]. 电力系统自动化, 2014, 38(14): 17-22.
PAN Xiong, WANG Lili, XU Yuqin, et al. A wind farm power modelling method based on mix Copula [J]. Automation of Electric Power Systems, 2014, 38(14): 17-22.
[20] HAGSPIEL S, PAPAEMANNOUIL A, SCHMID M, et al. Copula-based modeling of stochastic wind power in Europe and implications for the Swiss power grid [J]. Applied Energy, 2012, 96(1): 33-44.

