涡轮叶片双排气膜冷却效率叠加计算准确性研究

孟通, 朱惠人, 刘存良, 徐博涵

(西北工业大学动力与能源学院, 710072, 西安)

随着现代涡轮发动机技术的发展,涡轮前温度逐渐提高,涡轮叶片的热负荷随之增加,因此需要先进的冷却方式来保证发动机热端部件的正常工作[1]。典型的涡轮叶片外部冷却方式为气膜冷却,即在涡轮叶片表面及端壁附近布置一排或多排离散气膜孔以达到冷却的目的。大部分的气膜冷却设计中都采用多排气膜孔的冷却方式,此时孔排气膜间存在相互作用,因此学者们对气膜间的流动换热规律以及如何准确地估算多排气膜的冷却效率方面做了大量的研究工作。

Han等最早对多排气膜冷却间相互作用的规律进行分析,并提出应用单排气膜冷却效率计算多排气膜冷效[2],然而影响最大、应用最广泛的是由Sellers基于双排的二维缝孔模型提出的计算方法[3],其基本原理可以概括如下。

首先,气膜冷却效率定义为由主流燃气温度Tg、壁面附近处的绝热壁面温度Taw以及冷气温度Tc共同组成的量纲为1的参数

(1)

在叠加计算的基本模型中,将前一级气膜的气膜掺混后的绝热壁温作为本级气膜的主流温度来计算本级的气膜冷却效率,经过推导可以得到

(2)

式中:ηi(x)为第i排气膜单独存在时的气膜冷却效率。Sellers的叠加计算模型对于二维缝孔基本是准确的,但目前涡轮叶片中常用的气膜孔型为离散的三维气膜孔,因此许多学者对于此计算方法在三维气膜孔中的应用进行了研究。学者们首先研究了平板上的气膜冷却效率叠加规律。Han和Mehendale对气膜孔排距为2.5D且为叉排的平板双排气膜孔结构的叠加效率进行了分析研究,结果表明双排气膜孔结构的气膜冷却效率的直接测量值与通过单排气膜冷却效率的叠加计算值相比偏高[4]。Harrington等研究了平板上全气膜条件下绝热气膜冷却效率的叠加规律,其冷却结构为10排叉排圆形气膜孔,结果表明通过叠加所得冷却效率与测量值相比偏高[5]。Sasaki等通过实验研究了气膜孔间距为3D时冷却效率的叠加计算准确性,实验结果表明Sellers叠加计算值与实验测量值较接近[6]。Saumweber等研究了平板上双排气膜孔(包括圆柱型气膜孔和扇形气膜孔)的冷却效率叠加规律,研究表明Sellers叠加算法对于双排扇形气膜孔在低吹风比时,第2排孔下游10D后区域吻合较好,靠近第2排孔位置冷却效率偏低[7]。

在平板的基础上,学者们对涡轮叶片上的气膜冷却效率叠加规律进行了研究。Sakata等研究了涡轮导向叶片上的多排气膜冷却效率叠加规律,结果表明Sellers叠加计算方法与实验测量值吻合较好[8]。Mhetras和Luckey等研究了涡轮叶片上气膜冷却吹风比从1.0变化到2.67时的叠加计算规律,其值与实际值相近[9-10]。Anderson等研究了涡轮叶片前缘的气膜冷却效率叠加规律,结果表明高动量比下叠加计算值与实测值相比较低[11]。Schneider等研究了前缘气膜对压力面扇形孔冷却效率的叠加规律影响[12]。其他学者们对叠加计算的适用性同样进行了研究,但由于实验条件以及测量准确性等原因其结论不尽相同[13-15]。

因此,学者们在Sellers叠加公式的基础上进行了修正及改进。Andreini等对Sellers模型进行了改进并定义了叠加长度的概念[16]。朱惠人等在叠加公式的基础上引入了关于吹风比的参数[17]。Kirollos等对多排小孔间距结构的气膜冷却孔的Sellers公式进行了改型,从能量的角度出发重新计算了每层气膜的掺混温度,进而得出精确的气膜冷却效率并与实验结果进行对比,结果表明基于能量的叠加算法在小孔间距下对冷却效率预测较准确[18]。

针对目前国内外关于涡轮叶片上气膜冷却效率叠加规律研究较少的现状,且多为对Sellers叠加计算公式适用性验证研究,而没有考虑实际情况下孔排间相互作用的冷却机理,本文针对3种典型的影响气膜冷却效率叠加计算的因素进行了实验及计算研究,总结其叠加规律,分析叠加机理并给出相应的叠加公式修正方法。本文丰富了相关研究内容,并可为多排孔冷却设计提供参考依据。

1　实验装置及测量方法

1.1　实验装置

实验在低速叶栅风洞中进行,实验系统如图1所示。系统主要包括主流系统及二次流系统两部分,其中主流系统包括离心风机、储气罐、进口稳定段、主流稳压箱、蜂窝器、收缩段、加热器、实验段等,实验二次流系统由离心风机、稳压储气罐、阀门、流量计、加热器等组成。实验中叶片及叶栅通道的参数如表1所示。

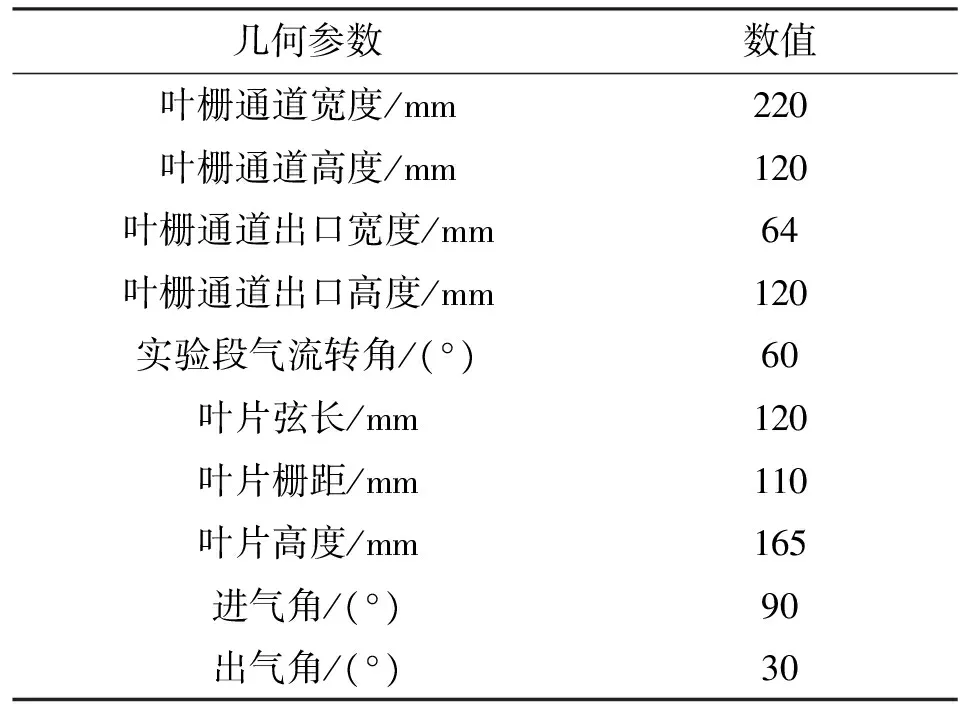
表1　叶栅及叶片几何参数

涡轮叶片实验件如图2所示,叶片采用光固化快速成型(3D打印)工艺加工而成,叶片材料为光敏树脂,加工误差在±0.1 mm以内。叶片吸力面及压力面共布置4排圆柱型气膜孔,其中压力面2排气膜孔,吸力面2排气膜孔,气膜孔径D=0.7 mm。为了研究每排气膜间的相互作用机理,需要对压力面及吸力面每排气膜的吹风比进行精确控制,因此实验件中位于压力面及吸力面的4排气膜孔,每排都分别供气。

图2　涡轮叶片实验件

1.2　实验测量方式

本文实验中采用红外测量的方法应用瞬态导热测量理论对叶片表面进行全表面测量。文献[19]对瞬态传热测量理论做了详细介绍,为本实验中的理论依据,本文不再赘述。实验中通过K型热电偶及4718温度采集模块对主流腔及二次流腔的温度进行测量,叶片表面温度通过Xenics Gobi-640-GigE红外相机测量,相机的像素为640×480。由于主流实验段不透红外光,因此在主流实验段处布置透光率约为0.92的锗玻璃。实验测量中红外相机的准确度受到红外相机本身的芯片温度的影响,因此将红外相机测量温度与标准热电偶测量温度相对比,从而对红外相机进行校准。4种芯片温度的校准结果如图3所示。

1.3　数据处理方式实验误差分析

本文实验中主流与二次流温度通过K型热电偶测量,测量误差ΔTc=±0.2 K,涡轮叶片表面温度通过红外相机测量,测量误差ΔTR=±1 K,时间测量误差Δt=±0.1 s。根据误差传递公式,可以计算出实验中气膜冷却效率的误差约为6.2%[20]。

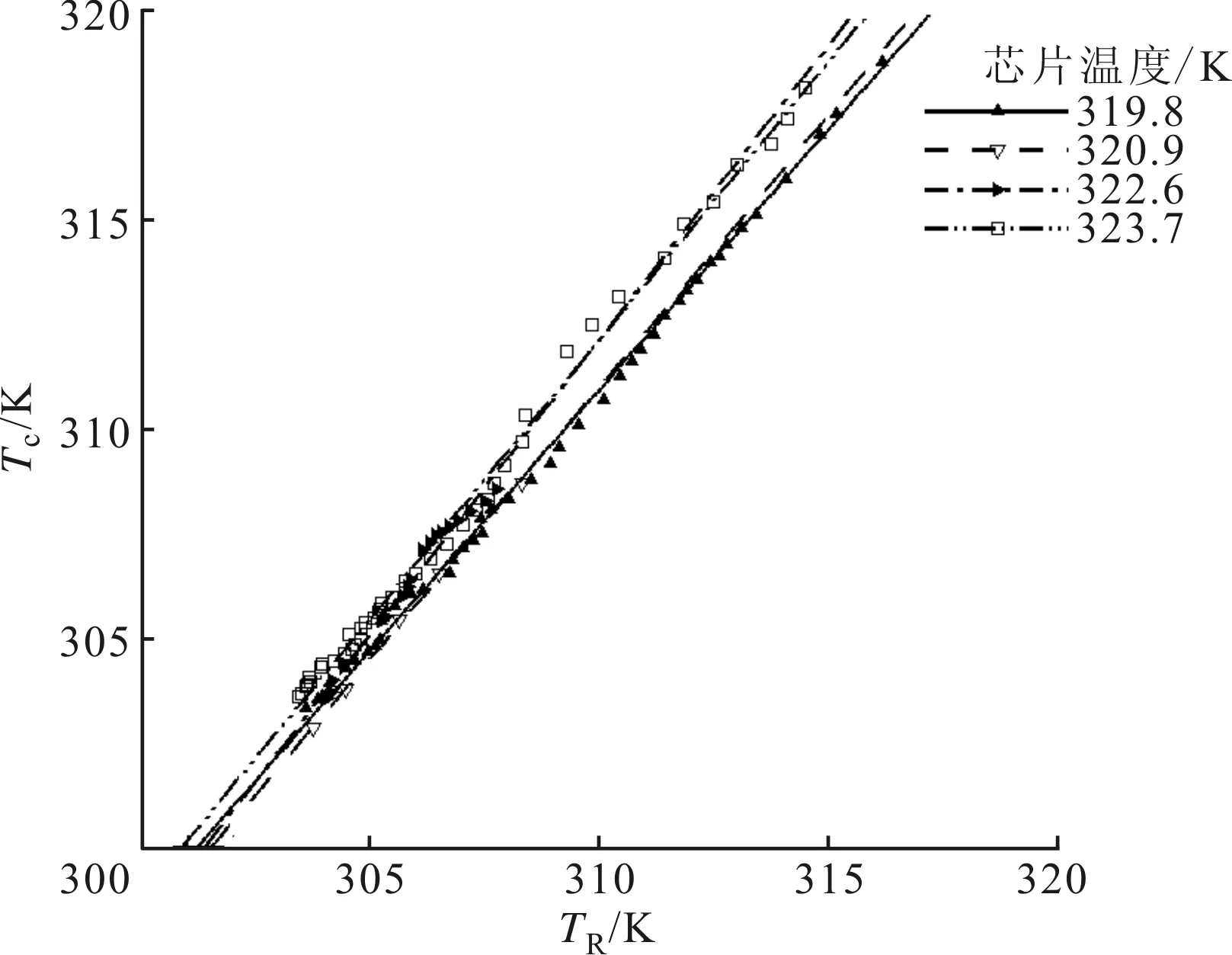
图3　红外相机校准曲线

2　计算模型及网格参数

2.1　物理模型

为了分析气膜孔排间的相互作用规律,本文采用了数值模拟方法对相应的实验工况进行计算研究。吸力面双排气膜孔的冷却效率计算模型如图4所示。在某型涡轮叶片基础上,分别在压力面及吸力面布置两排圆柱型气膜孔,气膜孔排布方式包括顺排及叉排两种排列方式。在沿叶高方向上气膜孔布局具有周期性,因此为节省计算成本在进行数值计算时,计算模型只取一个周期单元进行计算,在气膜孔两侧边界区域采用周期性边界条件,沿叶高方向计算单元内部包括5排气膜孔。计算模型中位于压力面及吸力面处的气膜孔直径D=0.7 mm,气膜孔间距P/D=3。叶片前缘气膜孔直径D=0.7 mm,气膜孔沿叶高方向展向偏角为90°。其余压力面气膜孔模型及单排气膜孔模型与之类似。

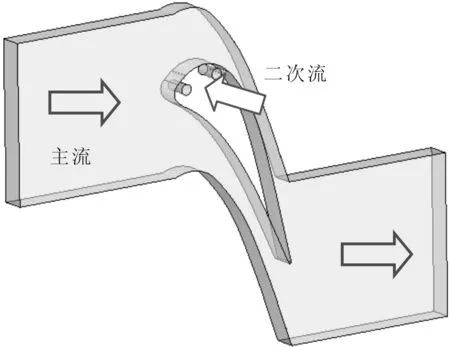
图4　吸力面双排孔数值模拟几何模型

2.2　计算网格及边界条件

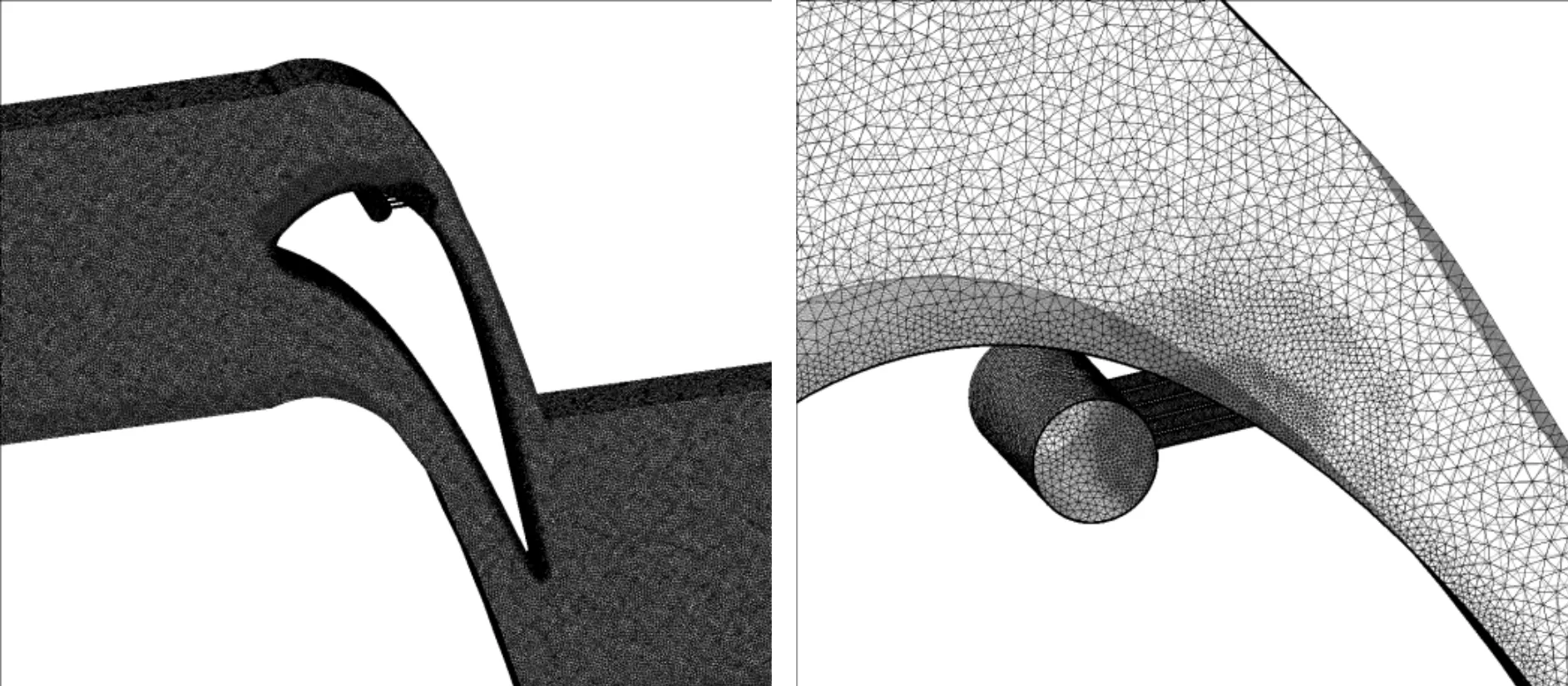
(a)计算网格图　　　　　(b)图格局部放大图图5　吸力面单排气膜孔数值计算网格

图6　网格无关性验证

本计算中网格均采用ICEM CFD 13.0生成。为了准确计算边界层内的速度和温度分布,对于增强壁面函数,要求邻近壁面的y+<1,因此各计算模型在气膜孔内以及邻近壁面处的网格均添加了Prism边界层进行了加密处理。近壁面处,边界层有15层,第1层厚度约为0.001 mm,增长比率为1.15,计算结果y+均在1附近,符合要求。图5为吸力面布置单排气膜孔的网格示意图。在进行计算前对网格无关性进行了验证,如图6所示,对3种数量的网格(例1为800万;例2为1 000万;例3为1 200万)进行对比,发现网格数增长至1 000万以上时,气膜孔后壁面温度分布已经基本不变,因此选用了1 000万的网格密度作为标准进行其他模型的网格划分。本文中数值计算采用SST湍流模型,壁面函数采用Scalable壁面函数。数值模拟研究中计算工况及边界条件根据实验工况设定,主流设置为速度入口边界条件,进口速度为20 m/s,主流温度为300 K,湍流度为1%。主流出口设置为压力边界条件,压力为1个大气压。二次流进口设置为质量流量入口边界条件,二次流温度为330 K,湍流度为5%。通过调整二次流质量流量控制吹风比,本文中吹风比从0.5增至2。数值模拟中为计算绝热气膜冷却效率,壁面设置为绝热壁面,计算所得温度为绝热壁面温度。

3　实验结果及分析

3.1　实验及计算工况

实验研究了主流雷诺数Re=86 500时压力面及吸力面双排气膜孔在不同吹风比M=0.5,1.0,1.5,2.0条件下的气膜冷却效率叠加特性。实验中主流雷诺数根据气膜孔直径定义

(3)

吹风比定义为

(4)

式中:Ug、ρg为主流速度及主流密度;Uc、ρc为气膜孔入口平均速度及二次流密度;μg为主流的动力黏性系数。

3.2　冷却效率叠加结果与讨论

本节中对涡轮叶片上压力面及吸力面的双排孔气膜冷却叠加特性进行了实验及数值计算分析,并对叠加公式进行了改良。

3.2.1涡轮叶片不同位置处的叠加规律涡轮叶片不同位置型面差异明显,吸力面为凸面,曲率较大,压力面为凹面,曲率较小,因此流体的气动状态在吸力面及压力面会呈现不同的分布规律。本文在研究叶片气膜冷却效率叠加规律前对实验叶片的气动规律进行了测量。图7为4种主流雷诺数下实验测量的叶片压力系数Cp分布。从图中可以看出,不同雷诺数下吸力面及压力面的压力系数分布规律基本相近。在吸力面上,压力系数从前缘开始迅速减小,而后有所提升。在压力面上,前缘区域内压力系数降低较快,之后在相对弧长S/S0=-0.05～-0.6范围内缓慢降低,随后再次迅速降低直至尾缘附近。叶片吸力面的曲率更大,叶栅通道内的流体沿着凸面流动,气流突然加速,伴随速度增加压力降低很快,随后出现局部的逆压区;叶片压力面前半段曲率较小,流体加速不明显,同样压力变化不大。整体上看,叶片压力面上的气流流动相对简单。

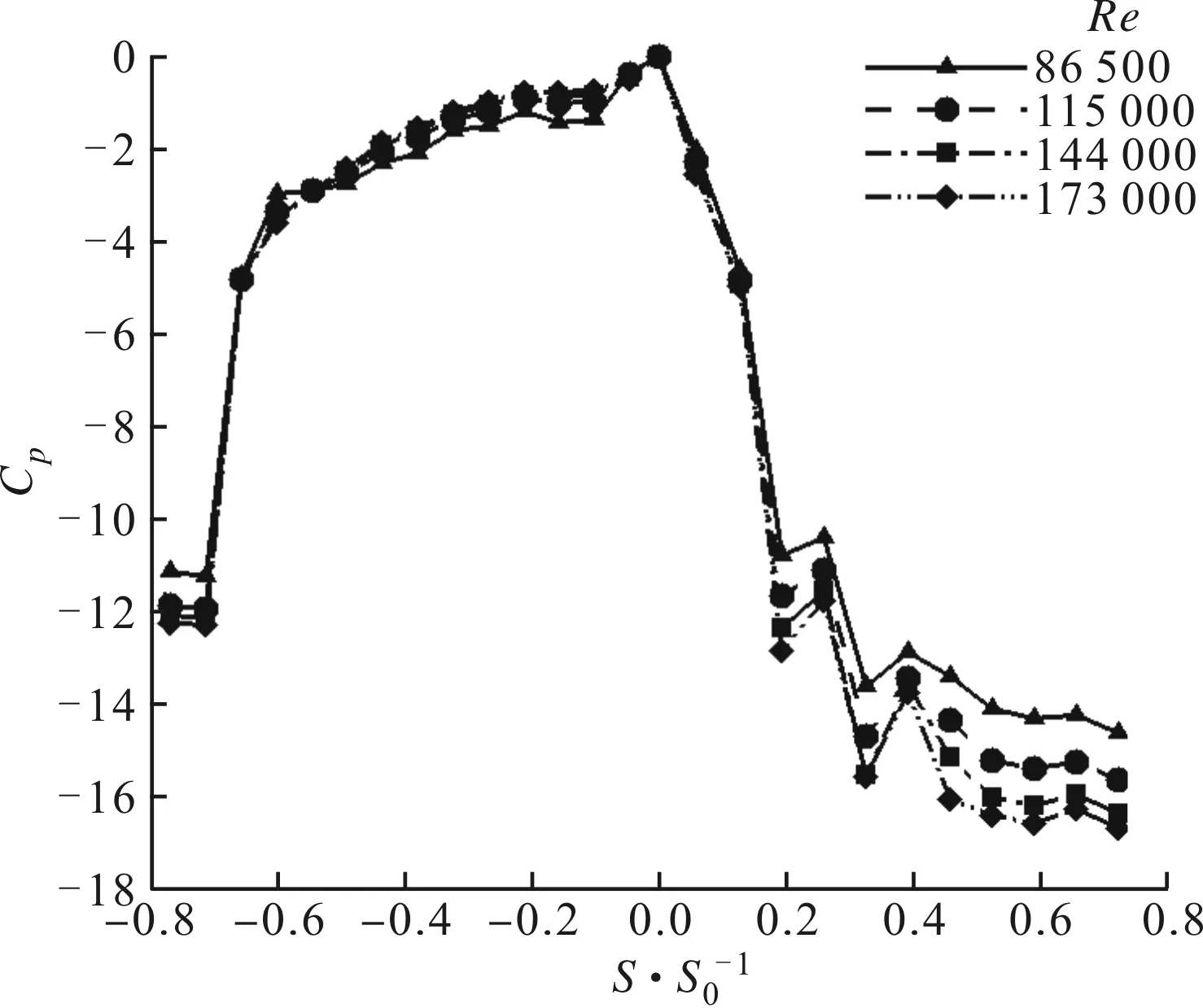
图7　4种主流雷诺数下实验测量的叶片压力系数分布

3.2.2叶片形状因素对叠加规律的影响图8为M=0.5时涡轮叶片吸力面第1排、第2排和双排气膜孔的冷却效率实验测量值及叠加计算的展向平均值。叠加计算值通过式(5)中Sellers叠加计算方法得出。从图中可以看出,单排及双排孔的冷却效率均随着孔下游气膜的逐渐发展而降低。M=0.5条件下第1排气膜由于吸力面的凸面的曲率作用,气膜脱离壁面的趋势增强,在第2排气膜孔附近冷却效率处于一个较低水平,已接近0.1。此时,两气膜间的相互作用较小,双排孔后气膜冷却效率主要受到第2排气膜孔的影响,因此叠加计算值与实验测量值相比虽然仍较高但在近孔区域(X/D<5)基本吻合,误差在5%范围内,在远孔区域(X/D>5)误差逐渐增大。

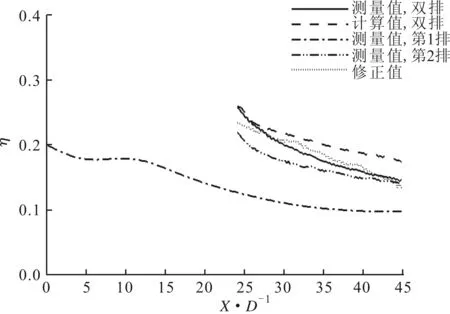
图8　M=0.5时吸力面冷却效率叠加规律

图9为M=0.5时涡轮叶片压力面第1排、第2排和双排气膜孔的冷却效率实验测量值及叠加计算的展向平均值。从图中可以看出,M=0.5条件下第1排气膜由于压力面的凹面的曲率作用,气膜较容易附着于壁面上,其在第2排气膜孔附近冷却效率仍较高,此时两排气膜间的相互作用较强。相比于叶片吸力面,压力面的叠加计算值偏高。从近孔区域至远孔区域,叠加计算值均高出实验测量值约13%。

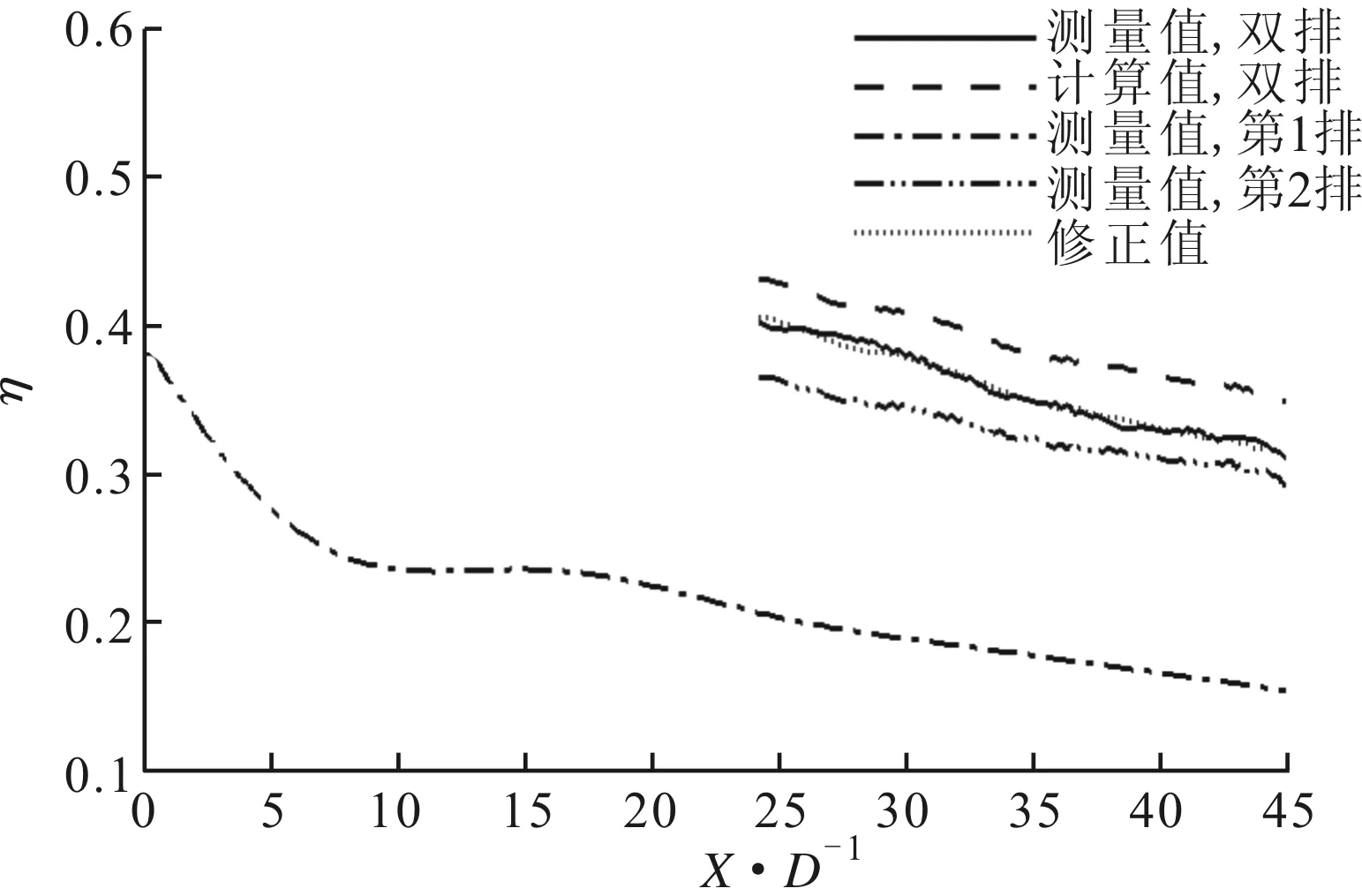
图9　M=0.5时压力面冷却效率叠加规律

(a)压力面第2排气膜孔前　(b)压力面第2排气膜孔后

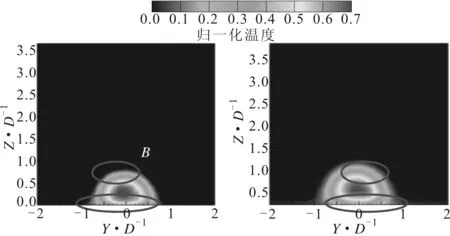
(c)孔后叠加计算结果　　　(d)孔后直接计算结果图10　压力面归一化速度场及温度场

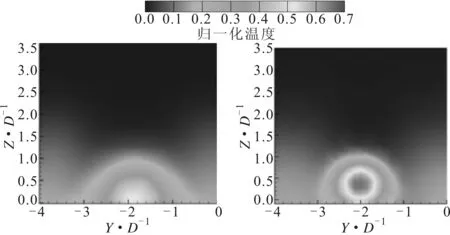
这种气膜间的作用规律可以在图10中观察到。图中为数值计算得到的第2排气膜孔沿流动方向孔前5D、孔后5D的归一化温度及速度场。第1排气膜在流出气膜孔后形成一组外卷对涡,如图中A区域所示。这股外卷涡对在第2排气膜孔壁面附近形成自壁面向上的流动趋势,对其附近流体产生“抽吸作用”,将第2排气膜向上拉升,此时前后排气膜间处于“层状叠加”的状态。当气膜孔排处于涡轮叶片吸力面时,单排气膜的脱离现象已较明显,因此双排气膜间这种抽吸作用相对不强烈,叠加计算值较准确。然而,当气膜孔排位于叶片压力面时,叶片凹面的作用使得气膜贴壁性较好,这种相互作用增强。如图中B区域所示,两排气膜间作用后,涡结构的范围扩大,涡中心远离壁面。应用叠加计算公式时考虑不到气膜间的这种相互影响,因此叠加计算结果有所偏高。

研究发现,叠加计算的准确性受到吹风比及沿流动方向的归一化距离X/D的影响,因此引入参数M及X/D对叠加公式进行修正,其形式为

(5)

式中:η为双排气膜孔后气膜冷却效率叠加值;η1、η2为只存在单排气膜孔时第1排、第2排气膜孔后的冷却效率;C为修正系数,包含M及X/D。此修正公式对应的实验工况为Re=86 000,叶片进气角为90°。

对于吸力面

C=50.1M(X/D)-1.12M-

74.8(X/D)+2.61

(6)

对于压力面

C=16.87M(X/D)+117.25M-

8.41(X/D)-57.75

(7)

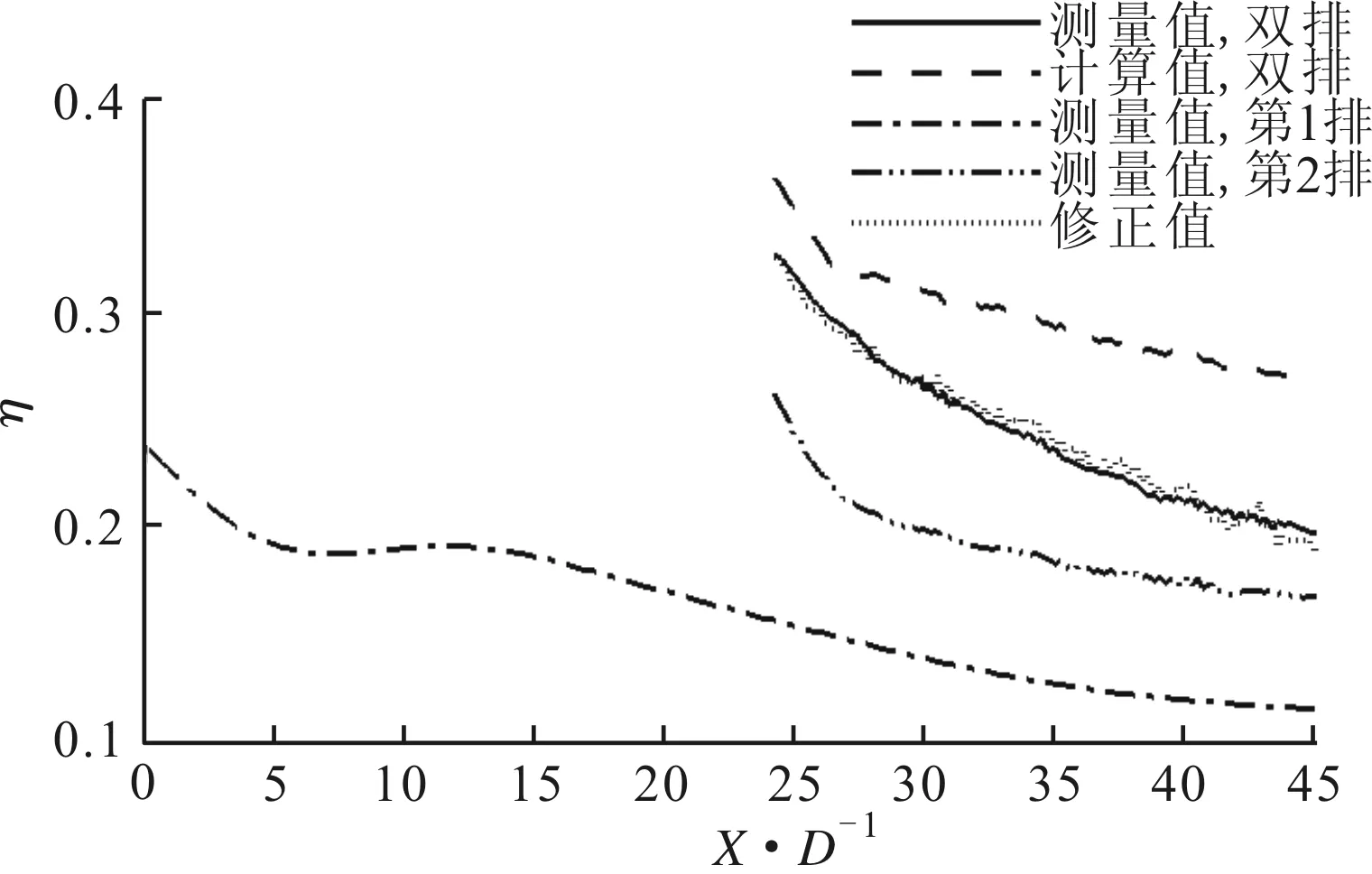
图11　M=1.0时吸力面冷却效率叠加规律

3.2.3吹风比对叠加规律的影响图11为M=1.0时吸力面第1排、第2排和双排气膜孔的冷却效率实验测量值及叠加计算的展向平均值。从图中可以明显看出,随着吹风比的增加,冷气量增多,相同壁面曲率条件下气膜冷却效率有所提高。第1排气膜孔的冷却效率在第2排气膜孔后有所提升,双排孔后区域受两排气膜孔共同作用,此时第1排气膜的叠加作用变得明显。通过Sellers叠加计算的气膜冷却效率相比于实验测量结果的误差增大,近孔区域约为8%,远孔区域约为17%,但由于吸力面的型面曲率作用,气膜脱壁性增强,总的来说两排气膜间相互干扰不如压力面明显。根据上节,将叠加计算方法修正为

C=24.87M(X/D)-0.53M-12.8(X/D)-2.42

(8)

图12为吹风比增加至1.0时压力面第1排、第2排和双排气膜孔的冷却效率实验测量值及叠加计算的展向平均值。与吸力面情况相类似,随着吹风比的增加,双排孔后区域受两排气膜孔的共同作用增强,前排气膜对后排气膜的抽吸作用更明显。通过Sellers叠加计算的气膜冷却效率相比于实验测量结果的偏差进一步增大,误差整体约为16%。因此,将叠加计算方法修正为

C=68.53M(X/D)+10.02M-

34.29(X/D)-3.81

(9)

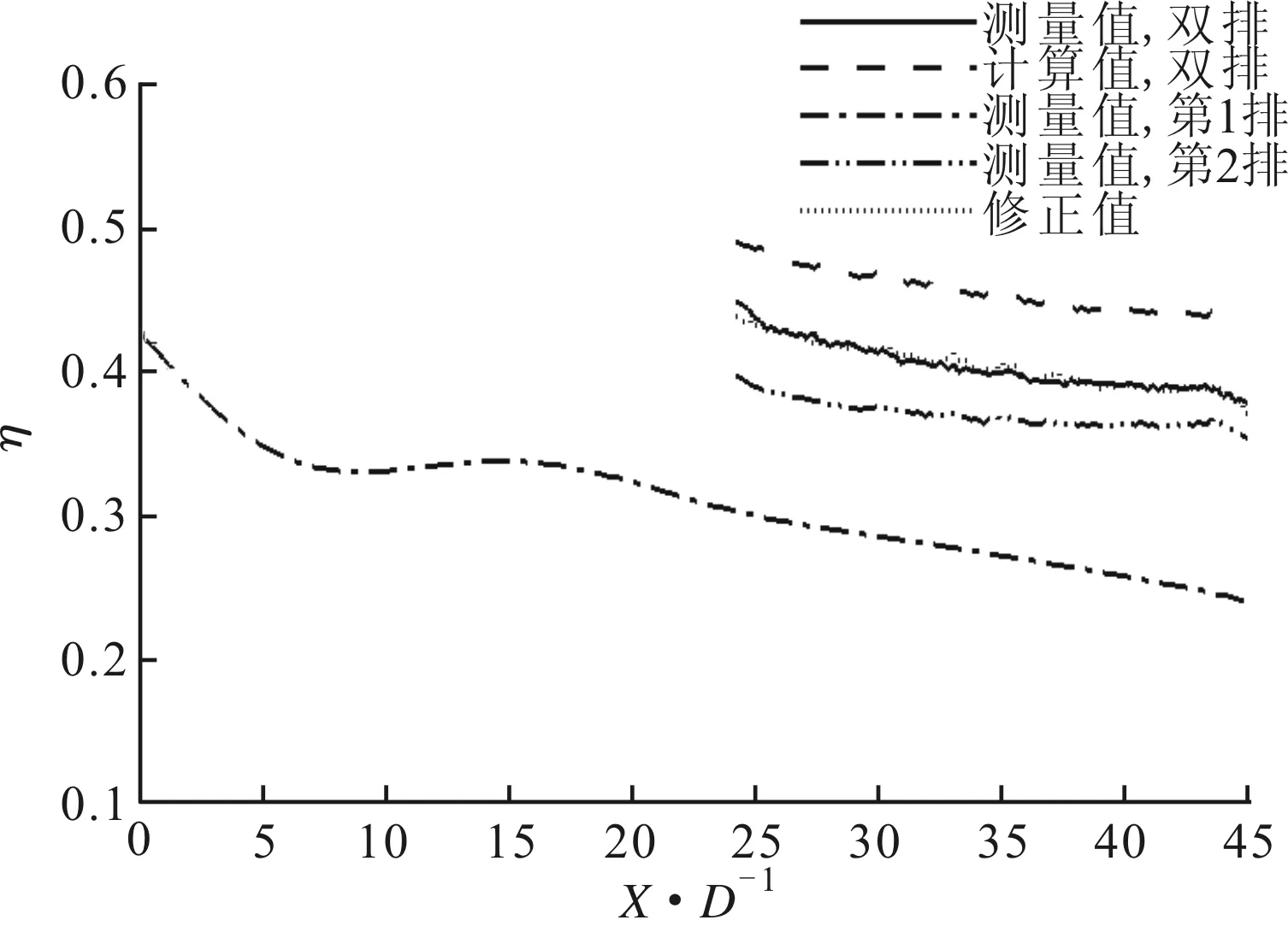
图12　M=1.0时压力面冷却效率叠加规律

图13为第2排气膜孔沿流动方向孔后5D的归一化温度场,吹风比对气膜间相互作用的影响可以在图中清晰地观察到。相比于图10中叠加计算结果与直接计算结果之间的区别,当吹风比增大时由于前排气膜的抽吸作用所带来的第2排孔后涡结构脱离壁面的现象更明显(框线区域C),因此通过叠加计算的壁面冷却效率有较大的误差。

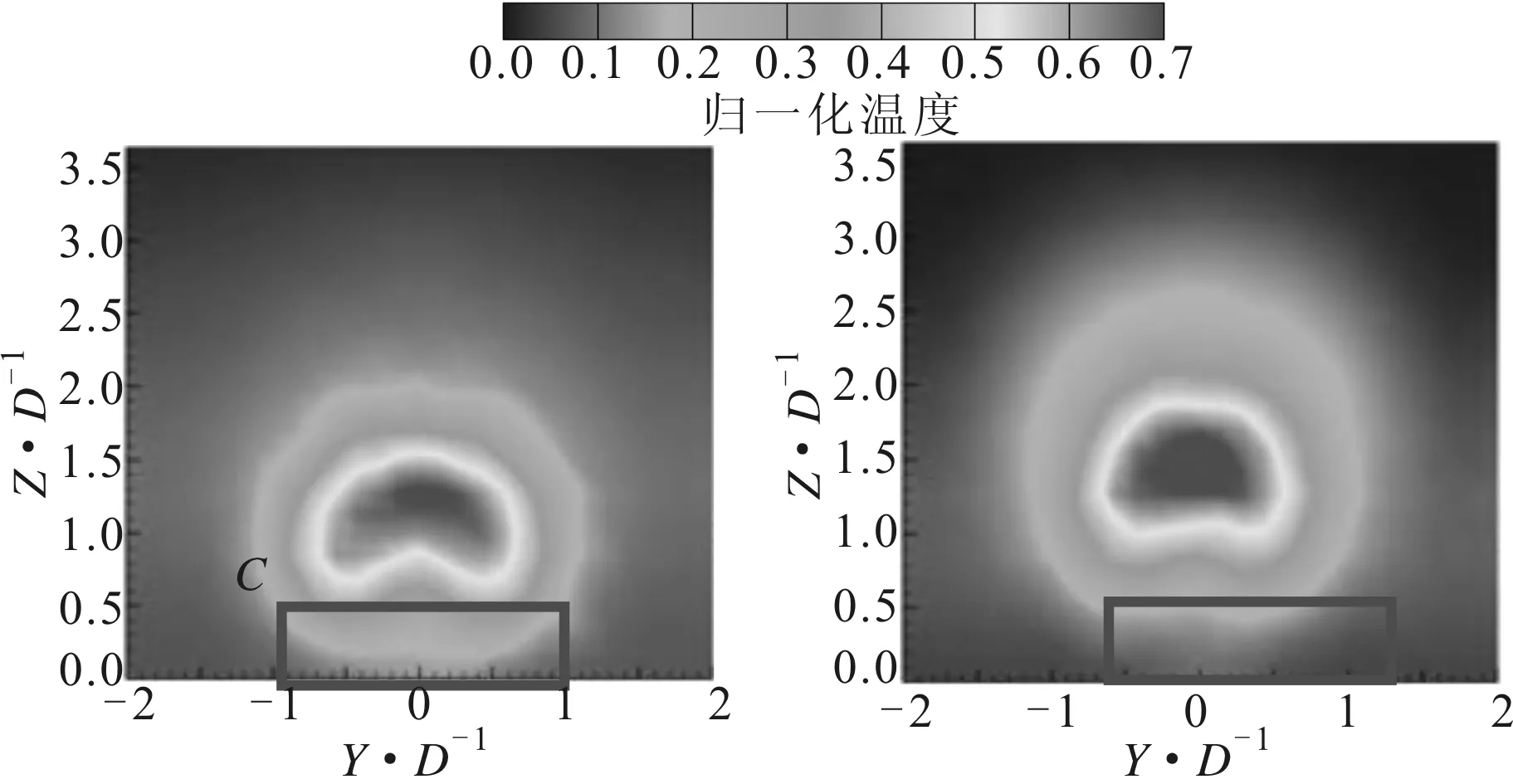
(a)Sellers叠加计算结果　　(b)双排孔后计算结果图13　压力面归一化温度场

3.2.4排列方式对叠加规律的影响图14、图15为M=0.5时双排气膜孔间叉排布置时吸力面以及压力面的冷却效率展向平均值。从图中可以看出,对比图8、图9的实验结果,当气膜孔排列方式改为叉排结构时,叠加计算的结果与实验测量值间的误差减小。在涡轮叶片吸力面,从第2排孔近孔区域至远孔区域叉排结构的叠加计算值与实测值均较接近,二者间最大误差小于5%。在涡轮叶片压力面,第2排孔后近孔区域叠加计算值稍有偏高,远孔区域叠加计算较准确。这种现象与叉排结构中双排气膜间的相互作用规律紧密相关。

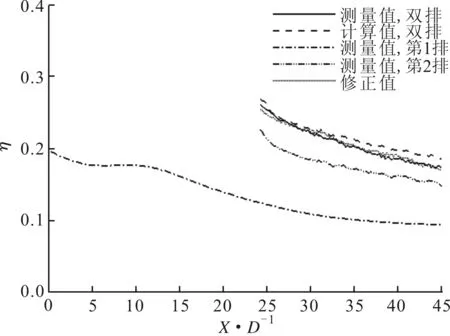
图14　吸力面叉排结构冷却效率叠加规律

图16为M=0.5时压力面叉排结构第2排气膜孔沿流动方向孔前5D、孔后5D的归一化温度场及速度场。从图中可以看出,与顺排结构前后两排气膜涡结构直接作用不同,对于气膜孔叉排结构,前后两排气膜孔间交叉排列,两排气膜孔后反转对涡交叉排开(图中A、B两组对涡),为“块状叠加”方式,这两组对涡在交界处转向相反,因此有相互挤压的作用,气膜被压向壁面,同时提高了冷气的贴壁性。因此,通过叠加计算所得的温度场温度分布较均匀,与实际温度场间差异较小。

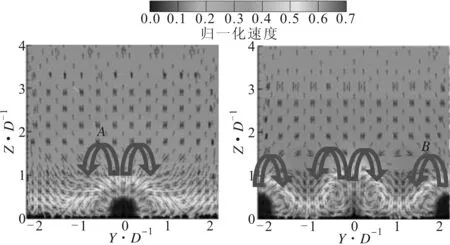
(a)压力面第2排气膜孔前　(b)压力面第2排气膜孔后

(c)孔后叠加计算结果　　　(d)孔后直接计算结果图16　压力面叉排结构归一化速度场及温度场

4　结　论

本文根据瞬态导热测量理论,采用红外测量技术对涡轮叶片双排气膜冷却效率叠加特性进行了实验研究,并辅以数值模拟计算方法对其叠加的流动机理进行了分析,主要结论如下。

(1)受涡轮叶片压力面及吸力面型面曲率的影响,气膜冷却效率叠加计算的准确性有所区别。叶片吸力面型面为凸面且曲率较大,气膜吹脱现象明显,叠加计算误差较小。叶片压力面型面为凹面且曲率较小,气膜贴壁性强,叠加计算偏差大。

(2)吹风比对气膜冷却效率叠加计算准确性有较大影响,低吹风比时叠加较准确,高吹风比时误差较大。当叠加计算误差较大时,本文针对Sellers叠加公式提出了相应的修正。

(3)气膜孔排布方式对冷却效率叠加计算结果准确性有影响。气膜孔叉排布置时,前后排气膜间呈现“块状叠加”现象,气膜间干扰较弱,叠加计算结果较准确。气膜孔顺排布置时,前后排气膜呈现“层状叠加”现象,气膜间相互干扰增强,叠加计算结果偏高。

参考文献:

[1]葛绍岩, 刘登瀛, 徐靖中, 等. 气膜冷却 [M]. 北京: 科学出版社, 1985: 1-5.

[2]HAN J C, SKIRVIN S C, HAYES L E, et al. Film cooling with multiple slots and louvers [J]. Journal of Heat Transfer, 1961, 83(3): 281-291.

[3]SELLERS J P. Gaseous film cooling with multiple injection stations [J]. AIAA Journal, 1963, 1(9): 2154 -2156.

[4]HAN J C, MEHENDALE A B. Flat plate film cooling with steam injection through one row and two rows of inclined holes [J]. Journal of Turbomachinery, 1986, 108(1): 137-144.

[5]HARRINGTON M, MCWATERS M, BOGARD D G, et al. Full coverage film cooling with short normal injection holes [J]. Journal of Turbomachinery, 2001, 123(4): 798-805.

[6]SASAKI M, TAKAHARA K, KUMAGAI T, et al. Film cooling effectiveness for injection from multirow holes [J]. ASME Journal of Engineering Power, 1979, 101(1): 101-108.

[7]SAUMWEBER C, SCHULZ A. Interaction of film cooling rows: effects of hole geometry and row spacing on the cooling performance downstream of the second row of holes [J]. Journal of Turbomachinery, 2003, 126(2): 101-110.

[8]SAKATA K, USUI H, TAKAHARA K. Cooling characteristics of film cooled turbine vane having multi-row of ejection holes [C]∥ASME 1978 International Gas Turbine Conference and Products Show. New York, USA: ASME, 1978: V01AT01A021.

根据设定的情景条件，对5个影响因素每隔0.5 h采集一次样本数据，采用调查问卷法得到影响因素的定性判定数据。各因素风险状态划分为强+(A)，强(B)，中等(C)，弱(D)，弱-(E)5个状态。

[9]MHETRAS S, HAN J C. Effect of superposition on span wise film-cooling effectiveness distribution on a gas turbine blade [C]∥ASME 2006 International Mechanical Engineering Congress and Exposition. New York, USA: ASME, 2006: 477-487.

[10] LUCKEY D W, LECUYER M R. Stagnation region gas film cooling: spanwise angled injection from multiple rows of holes: NASA contractor report 165333 [R]. Washington, USA: NASA, 1981.

[11] ANDERSON J B, WINKA J R, BOGARD D G, et al. Evaluation of superposition predictions for showerhead film cooling on a vane [J]. Journal of Turbomachinery, 2015, 137(4): V05BT13A032.

[12] SCHNEIDER M, PARNEIX S, VON WOLFERSDORF J. Effect of showerhead injection on superposition of multi-row pressure side film cooling with fan shaped holes [C]∥Proceedings of the ASME Turbo Expo 2003. New York, USA: ASME, 2003: 559-568.

[13] KINELL M, UTRIAINEN E, NAJAFABADI H N, et al. Comparison of gas turbine vane pressure side and suction side film cooling performance and the applicability of superposition [C]∥ASME Turbo Expo 2012: Turbine Technical Conference and Exposition. New York, USA: ASME, 2012: 1479-1489.

[14] CUTBIRTH J M, BOGARD D G. Evaluation of pressure side film cooling with flow and thermal field measurements [J]. Journal of Turbomachinery, 2002, 124(4): 670-677.

[15] ANDREINI A, CARCASCI C, GORI S, et al. Film cooling system numerical design: adiabatic and conjugate analysis [C]∥Proceedings of the ASME Summer Heat Transfer Conference. New York, USA: ASME, 2005: 9-20.

[17] 朱惠人, 郭涛, 许都纯. 双排簸箕形孔气膜冷却效率及其叠加算法 [J]. 航空动力学报, 2006, 21(5): 814-819.

ZHU Huiren, GUO Tao, XU Duchun. Film cooling and superposition method for double row dust-pan shaped holes [J]. Journal of Aerospace Power, 2006, 21(5): 814-819.

[18] KIROLLOS B, POVEY T. An energy-based method for predicting the additive effect of multiple film cooling rows [C]∥ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. New York, USA: ASME, 2013: V03BT13 A039.

[19] 刘存良. 新型高效气膜孔冷却特性研究 [D]. 西安: 西北工业大学, 2009.

[20] MOFFAT R J. Describing the uncertainties in experimental results [J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17.

[本刊相关文献链接]

王瑞琴,高炎,晏鑫,等.燃气透平尾缘开缝区冷却性能的非定常研究.2017,51(12):98-103.[doi:10.7652/xjtuxb201712 015]

翟颖妮,刘存良.高主流湍流度下大倾角异型气膜孔冷却特性实验研究.2017,51(7):16-23.[doi:10.7652/xjtuxb201707 003]

范小军,杜长河,李亮,等.4种冷却结构对叶片前缘流动换热影响的比较研究.2017,51(7):37-43.[doi:10.7652/xjtuxb201707006]

杜长河,范小军,李亮,等.旋转半径和叶片安装角对动叶旋流冷却流动和传热特性的影响.2017,51(5):37-42.[doi:10.7652/xjtuxb201705006]

杜长河,范小军,李亮,等.抽吸孔对旋流和冲击冷却流动传热特性的影响.2017,51(1):19-24.[doi:10.7652/xjtuxb 201701004]