细胞带电分析中显微细胞聚集度的数值表征方法
何佳熹, 钟力生, 宋晓源, 张新桐, 靳勐, 邱闽晨, 高景晖
(西安交通大学电力设备电气绝缘国家重点实验室, 710049, 西安)
实现细胞膜电荷特性测量是国际生物电磁学研究领域的一个重要课题[1-4]。通过研究细胞膜的电荷特性,有望分析和表征细胞的功能变化,为相关疾病的检测和治疗提供物理手段,对深入认识电磁生物效应具有重要意义[5]。在细胞悬液中,细胞表面带电状况与细胞的团聚密切相关,因此在进行细胞显微观察时,观测细胞团聚程度是判断细胞带电状况的一种实验手段。
目前,通过显微观察判断团聚程度的方法大多凭借主观识别[6-8],没有统一的计算方法。要实现细胞团聚程度的测量和计算,首先需要对细胞位置和浓度进行判断,有许多方法可用于对低浓度细胞的精确识别[9-11],但是当图中细胞浓度很高,甚至人眼观察都无法准确识别每个细胞的位置时,设计精确识别细胞的算法就较为困难。此外,显微观察时,视野中细胞数量通常存在一定差异,而细胞数量对于细胞团聚的影响又会给细胞团聚程度的观测带来主观因素。
本文通过考察细胞显微图像灰度从而读取图像中细胞所处位置和密度,并由此通过计算细胞中心距倒数的平均值定义了细胞聚集度,建立了计算细胞团聚程度的方法。在此基础之上,采用MATLAB软件,实现了对显微图像的分析与重构,建立了使用细胞聚集度分析细胞表面电荷变化的方法,一定程度上解决了使用细胞聚集度定量判断细胞带电状况的问题。
1 图像的读取与划分
为了从细胞显微观测图像中获得细胞的聚集度,首先需要对图像中细胞所处的位置和密度进行读取。为此,本文设计了如图1所示的图像读取步骤。
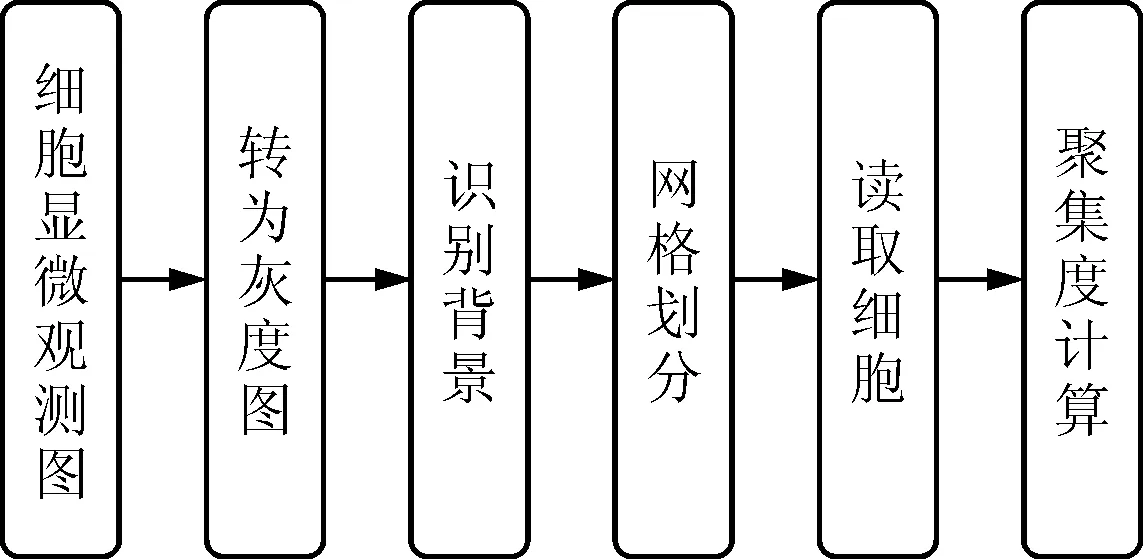
图1 细胞图像读取步骤
1.1 显微图像灰度处理
为了简化处理,本文先将如图2a所示的显微观测图像保存为如图2b所示的灰度图,使用二维灰度矩阵来存储和处理图像;再使用MATLAB软件读取图像数据并按照像素保存成矩阵形式,其中矩阵每个元素的值都是0-1的双精度浮点数,并在需要时将其显示出来。
1.2 背景识别
如图2b所示,首先要识别图像中的背景部分,将背景和细胞加以区分。考虑到分散的细胞通常灰度分布区间较大,而观察背景的灰度范围通常集中在较窄的区间之内。本文采用读取整个图片灰度众数的方法确定背景灰度,即认为整张图片中按照像素出现次数最多的灰度为背景灰度。

(a)血细胞显微观测图
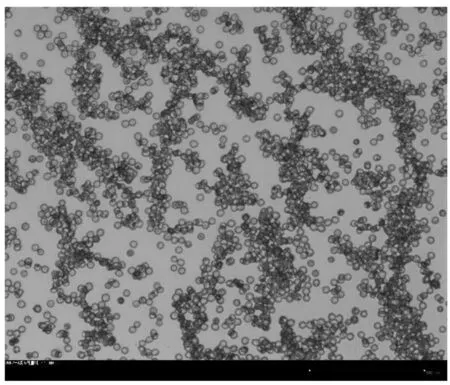
(b)显微观测灰度图

(c)显微观测网格剖分图图2 血细胞显微观察与网格剖分图
1.3 划分网格
实验中的细胞实际形状通常较为复杂且在很多时候难以精确识别,需要建立一种简化的识别方法来确定细胞所处位置。本文将整个图像按照一定边长划分为网格,根据细胞在图像中的实际大小确定网格边长,图2b中观测区域为1 024×1 280像素。像素单元对应边长约为0.3 μm,每个细胞直径约为15~20像素,因此为方便计算,将网格划分为边长为16像素的方格。细胞显微观测区域网格剖分结果如图2c所示。
1.4 网格中细胞密度识别
识别每个网格中的细胞是图像读取过程中的关键一步,对于细胞位置和分布的精确识别直接影响到后续计算结果的准确性。一些文献研究了处理红细胞图像的方法[10-11],但是对细胞的精确识别依旧较为困难且多数算法较为复杂。为此,本文给出了一种简便地识别网格中细胞位置和密度的方法,满足计算基本要求。
首先计算每个网格中的平均灰度,然后依据平均灰度与背景灰度之差是否大于预设值a来判断该点是否存在细胞;接着需要判断每个方格中的细胞密度。经过对图像地分析发现,在细胞较少的网格中,细胞与边界及细胞表面不同区域之间区分度较为明显。因此,网格中不同区域灰度差别较大,而细胞较多处网格中的细节区分度较差,边界较难区分,也即网格中的灰度差别较小。

(a)各参数细胞读取结果

(b)人眼读取结果与对应区域显微观测图的对比

(c)a=0.15,b=0.1细胞读取结果放大图图3 划分读取后细胞分布图
虽然程序读取和人眼读取结果采用不同的标准,但在后续计算中,对细胞密度之和按概率分布进行了归一化处理,因此在一张图中只有格点密度与所有格点密度和之比会影响计算结果,只要其相对密度准确就可以保证计算结果的准确性,按照不同标准读取密度并不会对后续计算结果产生影响。若要比较不同读取结果的细胞相对密度,就需要先将图3a中格点对应密度之和进行统一。为比较图3a中各图与图3b的密度差,本文将图3a中各图细胞总数全都统一成与图3b相同,并保持细胞相对密度不变。在此基础上,本文按下式比较了图3a上1/4部分和图3b人眼读取结果的二阶偏差
(1)
式中:n为对应网格中总格点数;a、b分别为图3a对应图像和图3b中各格点密度之和;A(i,j)、B(i,j)分别为图3a对应图像和图3b对应的格点矩阵第i行第j列对应元素。Δ2越小表明两矩阵之间差距越小。Δ2的计算结果如表1所示,可见a=0.15、b=0.1时,读取结果和实际情况最为接近,既包含了图2中有细胞的区域,又排除了背景区域,同时读取的细胞密度和实际情况也有很好的对应关系。因此,本文最终选取a=0.15、b=0.1,放大结果如图3c所示。
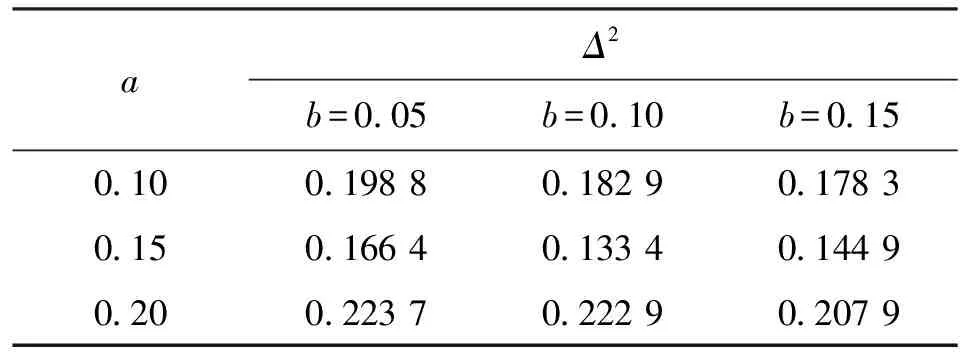
表1 不同参数读取结果与人眼观察的二阶偏差
在进行以上处理后,为减少存储空间和运算量,可以将细胞的位置保存在三列一维向量中,三列向量分别保存细胞的横纵坐标和该坐标点的细胞密度,并且可将不存在细胞的点删去。
2 聚集度的计算
2.1 聚集度计算模型
当考察外界因素对于细胞团聚程度的影响时,通常希望能够排除视野内细胞数量不同造成的细胞团聚程度差异的影响。由于正态分布是最为常见的分布状况,并且正态分布的标准差σ表示了分布的离散程度,这与本文中的聚集度具有类似的意义。因此,本文选取不同标准差σ的正态分布为例进行举例说明。如图4所示,标准差σ=3和σ=5,随机取100个和300个散点的结果,同一张图中颜色越深的点表示该点散点数越多。其中通过直观观察可以看出,当散点数相同的时候σ=3的散点团聚程度明显小于σ=5的散点。通过直观观察也很容易认为当σ相同时,300个散点的团聚程度高于100个散点。这种由于视野内细胞个数增加造成的细胞团聚程度的增加,很多时候是在考察细胞团聚程度时希望避免的。
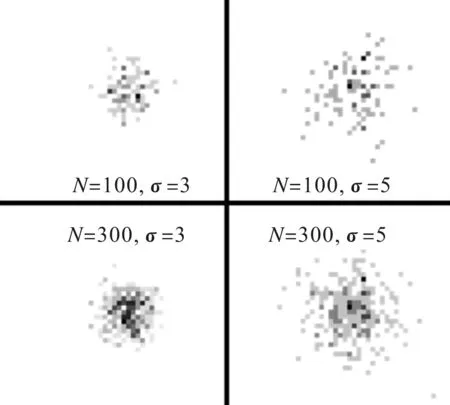
图4 正态分布随机散点图
为计算细胞团聚程度,需要将细胞团聚程度抽象为一个数学问题。本文提出如下建模方法:假设细胞在图2所示的二维平面上概率密度分布为f(x,y),则该问题抽象为构造一个关于f的参数聚集度δ来表示细胞团聚程度。根据图2~图4,以及前文提出的避免细胞个数对细胞团聚计算结果的影响,本文提出判断细胞团聚的以下几个要求。
(1)在细胞数量相同的情况下,与一个细胞邻近的细胞越多,则细胞聚集度越大,如图4中标准差较小的图片具有较大的聚集度。即任意两对细胞,若其中心距有d1
(2)细胞聚集度主要受邻近几个细胞的影响而与相对较远处的细胞基本无关。根据图2可以看出,在半径约为10个细胞直径范围内的细胞数量对细胞聚集度影响较大,而相距在10个细胞直径以上处的细胞数量对细胞聚集度影响较小,如图2中左上角的细胞团聚和右上角的细胞团聚基本无关。为此若两细胞中心距为1时对δ的影响为Δδ1,两细胞中心距大于10时影响为Δδ2,应有Δδ1≫Δδ2,或Δδ1>10Δδ2。
(3)由于显微观察存在很大的随机性,当判断外界因素对细胞团聚影响时,需要排除显微图片中细胞个数的影响。如图4中散点数造成的聚集度影响应被排除,即当细胞分布f(x,y)确定时,δ应为一个与细胞总数N无关的数。
综合考虑以上3点要求,本文定义细胞聚集度δ为整张图片中细胞中心距的倒数的平均值,作为细胞团聚程度的表征参数,即
(2)
为在细胞散点图中估计参数δ,用每个格点中细胞数与总细胞数的比代替概率分布函数,将积分改写为求和,式(2)改写为
(3)
式中:n(x,y)为(x,y)处细胞数;N为图像中细胞总数。由于(x1,y1)=(x2,y2)时上述求和中分母为0,需要剔除每个细胞和其自身计算的情况,共N个,式(3)变为
δ=
(4)
即当估计参数δ时,只需要将每个细胞与其他细胞中心距倒数相加,然后除以细胞的两两组合数,即得到其细胞中心距倒数平均值的估计值。
在细胞所处位置取整之后,不同细胞间也会存在坐标相同的情况,即一个格点内存在多个细胞。当一个格点内存在多个细胞时,如果细胞在格点内呈平均分布,则式(2)中f(x,y)=1,但此时关于δ的积分难以解析计算。同时,考虑到格点内细胞不会完全重叠,直接令f(x,y)=1也和实际情况不符,对这种情况采取直接赋值处理,假设细胞平均中心距为0.5格,则其倒数为2。因此,当细胞处于同一格点时,利用式(4)进行累加时约定其累加值为2。
2.2 计算方法验证
针对图4中提出的4个正态分布图形,本文按照以上提出的计算方法对其聚集度δ分别进行了计算,计算结果如表2所示。由表2可以看出,σ=3的图像聚集度明显大于σ=5的图像,并且对于两种不同的标准差有σ与δ乘积近似相等。这是由于δ是散点中心距倒数的平均值,σ是散点正态分布的标准差,正比于散点中心距;同时标准差相同的图像,聚集度δ近似相等。由于正态分布取点的随机性,不同图像计算结果不可能完全相同,但是该计算结果已经很明显地反映了聚集度δ随图中散点正态分布标准差的变化趋势,且该结果仅与散点分布的聚集程度有关,与散点个数无关。因此,本文提出的计算方法满足了2.1节中提出的建模要求。
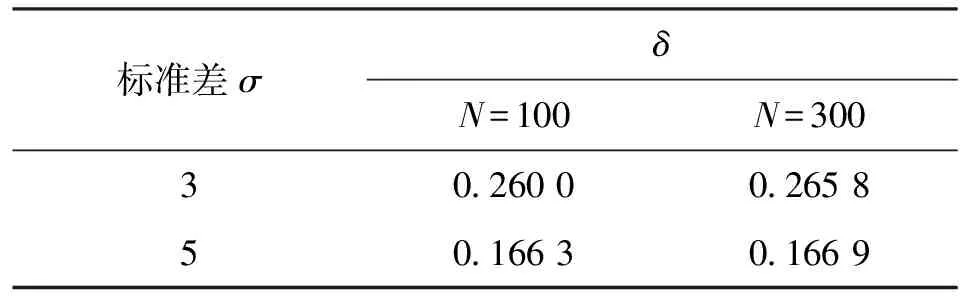
表2 正态分布聚集度δ计算结果
3 使用聚集度表征细胞表面电荷变化
3.1 细胞聚集度表征细胞表面电荷变化
由于唾液酸是细胞表面负电荷的主要载体,使用唾液酸酶可以将唾液酸残基从细胞表面去除,达到改变细胞表面电荷的作用[12]。为建立使用细胞聚集度分析细胞表面电荷的方法,本文使用4种不同浓度的唾液酸酶去除细胞表面唾液酸残基,并对其进行了10次显微观测,图5为其中一次的显微观测及之后的计算过程。

图5 血细胞聚集度计算过程
为验证血细胞团聚程度与唾液酸用量及细胞表面电荷的关系,并据此分析唾液酸酶对其表面电荷的影响,需要排除视野中细胞个数的影响,对血细胞团聚程度进行定量表征。实验中,对10次观测的结果利用式(4)计算细胞聚集度,并取其平均值和标准偏差,结果如图6所示。由于唾液酸酶能够去除细胞表面唾液酸,减少细胞表面带电和细胞间的相互排斥作用,理论上会造成细胞聚集度的增加。考虑到显微图像选取存在一定的随机性,实验中标准差较大,且添加0.005 U/mL的唾液酸酶聚集度δ计算结果大于0.02 U/mL,但仍可以认为实验结果在总体趋势上反映了聚集度δ随细胞表面电荷减小而增加的趋势,同时从图5中直观观察也可以得出类似的团聚程度变化规律。因此,可以认为当细胞聚集度δ增加时,表明细胞表面电荷减少,细胞间排斥作用减小,细胞趋于聚集;反之,当细胞聚集度δ减小时,表明细胞表面电荷增多,细胞间排斥作用增大,细胞趋于分散。
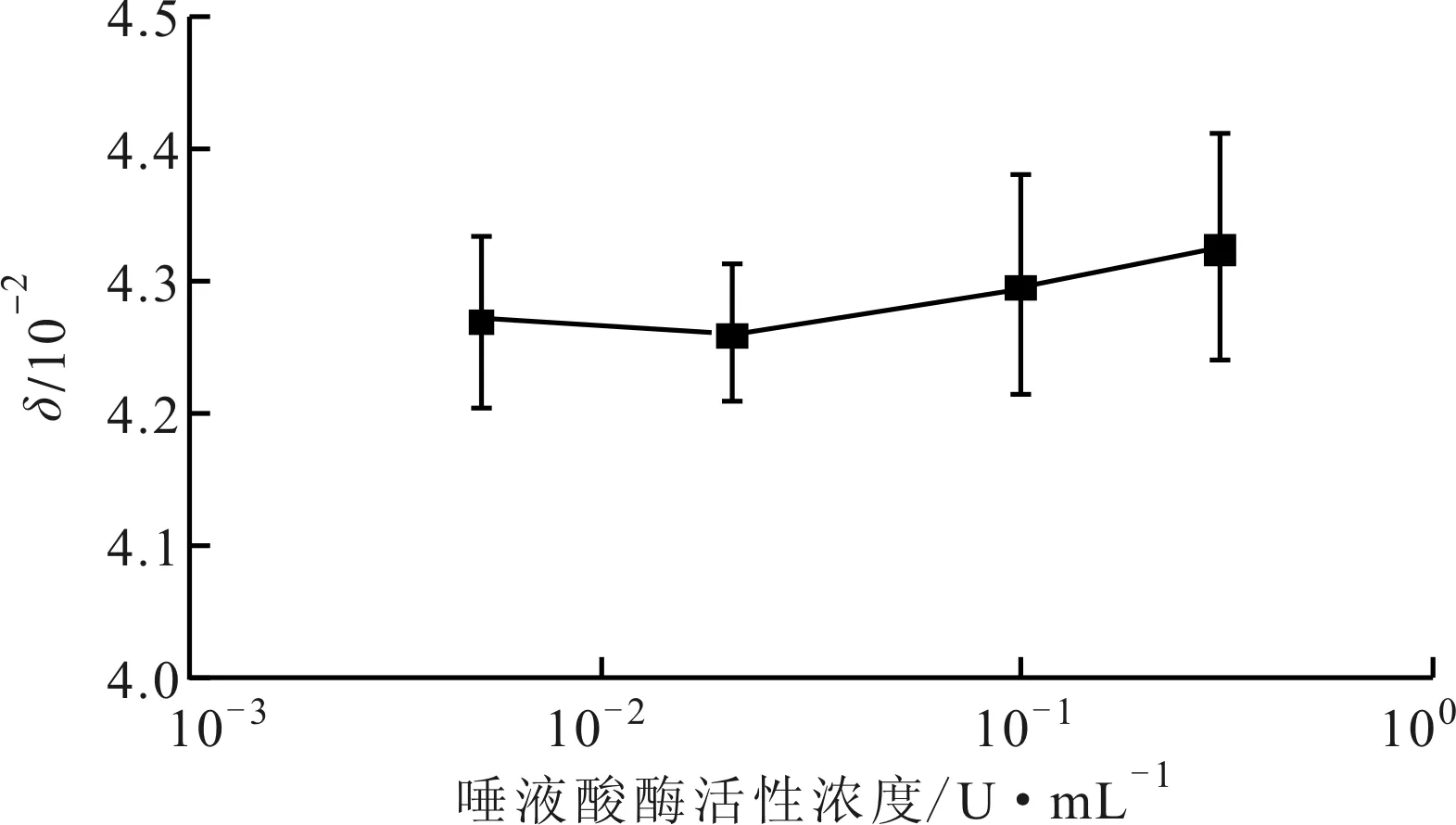
图6 血细胞显微观察聚集度计算结果
3.2 聚集度表征细胞表面电荷变化的有效性
为验证使用本文提出的方法计算细胞聚集度进而分析细胞表面电荷变化的有效性,本文使用ζ电位分析仪对细胞悬液的ζ电位进行了5次测量,实验结果如图7所示,由于细胞ζ电位为负值,为了使其变化趋势更加明显,图中使用了其绝对值。
ζ电位是细胞表面双电层中滑动层到溶液内部的电位差,正比于细胞表面电荷量[13-14]。实验中,唾液酸酶去除了细胞表面唾液酸残基,细胞表面负电荷减少,因而细胞表面ζ电位绝对值减少。同时由于细胞表面负电荷减少,细胞间相互排斥作用减弱,造成了细胞团聚作用增强。对比图6与图7中细胞聚集度δ与ζ电位变化曲线发现,当细胞表面ζ电位绝对值减小的时候,细胞聚集度表现出相似的上升趋势,验证了本文提出的使用细胞聚集度分析细胞表面电荷变化的有效性。本实验定性描述了细胞聚集程度和细胞表面电荷及ζ电位的关系,但是其定量分析还有待进一步研究。
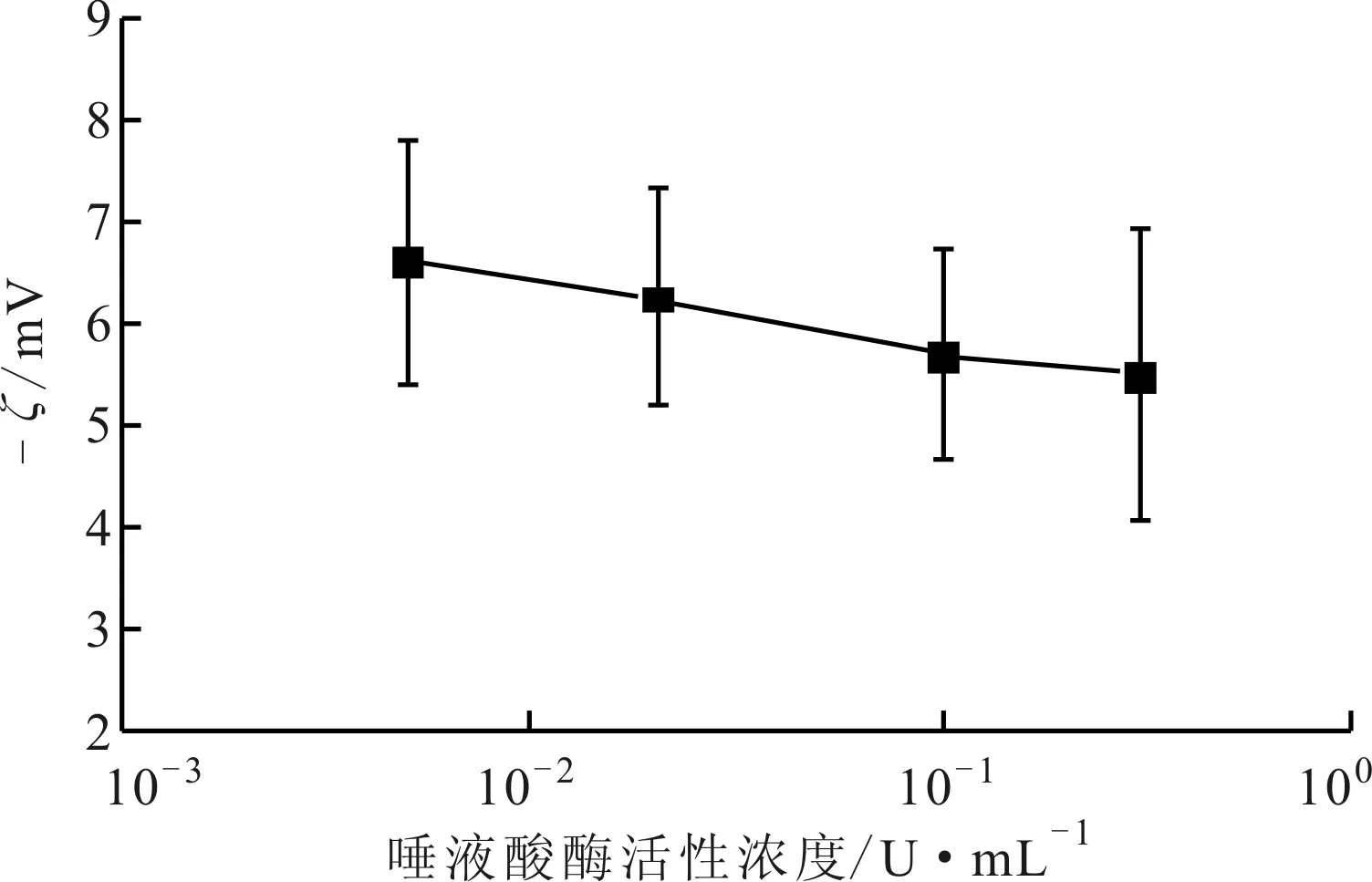
图7 血细胞ζ电位的实验结果
4 结 论
本文建立了一种基于细胞灰度图计算细胞聚集度并由此推断细胞表面电荷变化情况的方法,主要结论如下。
(1)提出了一种识别细胞所在位置和密度的计算方法;针对细胞数量不同的情况定义了细胞的聚集度,建立了基于细胞中心距倒数平均值计算细胞聚集度的方法;针对正态分布的情况验证了该计算方法的可靠性。
(2)在此基础之上,本文使用唾液酸酶改变细胞表面带电基团,建立了使用细胞聚集程度分析细胞表面带电状况的方法,发现当细胞聚集度δ增加时,表明细胞表面电荷减少,细胞间排斥作用减小,细胞趋于聚集;反之,当细胞聚集度δ减小时,表明细胞表面电荷增多,细胞间排斥作用增大,细胞趋于分散。
(3)通过测量细胞ζ电位验证了使用细胞聚集度反映细胞表面电荷变化的有效性,建立了使用细胞聚集度分析细胞表面电荷变化的数值计算方法。
本文方法可以在很大程度上排除视野内细胞数量对于细胞团聚程度的影响,从而使分析细胞表面电荷变化和细胞团聚程度的关系相比主观观察更具客观性。
本文方法不仅可以用于细胞团聚程度和表面带电状况的表征,在相似的胶体或浊液中也存在类似的聚集度[15]计算问题,对胶体或浊液中分散相的分散程度或团聚程度及其表面带电情况也可使用该方法进行类似分析。
参考文献:
[1]MACGREGOR R J. A possible mechanism for the influence of electromagnetic radiation on neuroelectric potentials [J]. IEEE Transactions on Microwave Theory and Techniques, 1979, 27(11): 914-921.
[2]CASTELLARNAU M, ZINE N, BAUSELLS J, et al. Integrated cell positioning and cell-based ISFET biosensors [J]. Sensors and Actuators: B, 2007, 120: 615-620.
[3]QIU Minchen, ZHONG Lisheng, SONG Xiaoyuan, et al. Relaxation polarization model of SD rat tissues at frequency range 42 Hz-5 MHz [C]∥2016 IEEE Conference on Electrical Insulation & Dielectric Phenomena, Piscataway, NJ, USA: IEEE, 2016: 743-746.
[4]HE Jiaxi, ZHONG Lisheng, CHENG Lin, et al. The influence of ultrasonic electrokinetic polarization on the dielectric constant of erythrocyte suspension [C]∥2016 IEEE Conference on Electrical Insulation & Dielectric Phenomena. Piscataway, NJ, USA: IEEE, 2016: 751-754.
[5]李缉熙, 牛中奇. 生物电磁学概论 [M]. 西安: 西安电子科技大学出版社, 1990: 1-10.
[6]WICK P, MANSER P, LIMBACH L K, et al. The degree and kind of agglomeration affect carbon nanotube cytotoxicity [J]. Toxicology Letters, 2007, 168(2): 121-131.
[7]李志华, 刘芳, 王晓昌. 影响微生物聚集体的聚集度的因素分析 [J]. 环境科学学报, 2010, 30(3): 456-462.
LI Zhihua, LIU Fang, WANG Xiaochang. Analysis of the factors that influence the aggregation-degree of microbial aggregates in sludge [J]. Acta Scientiae Circumstantiae, 2010, 30(3): 456-462.
[8]AMINOFF D, BELL W C, SARPOLIS K, et al. Role of sialic acid in survival of erythrocytes in the circulation: interaction of neuraminidase-treated and untreated erythrocytes with spleen and liver at the cellular
level [J]. Proceedings of the National Academy of Sciences of the United States of America, 1977, 74(4): 1521-1524.
[9]龚声蓉. 数字图像处理与分析 [M]. 2版. 北京: 清华大学出版社, 2014: 199.
[10] HO Z P, LEE H J. A new algorithm for red blood cell characteristics image recognition [C]∥International Conference on Multimedia and Signal. Piscataway, NJ, USA: IEEE Computer Society, 2011: 303-307.
[11] MAJI P, MANDAL A, GANGULY M, et al. An automated method for counting and characterizing red blood cells using mathematical morphology [C]∥Eighth International Conference on Advances in Pattern Recognition. Piscataway, NJ, USA: IEEE, 2015: 1-6.
[12] 谢利德, 姚伟娟, 孙大公, 等. 神经氨酸酶对红细胞膜的剪切弹性模量和表面粘度的影响 [J]. 中国生物医学工程学报, 2001, 20(1): 33-37, 60.
XIE Lide, YAO Weijuan, SUN Dagong, et al. Effect
of neuraminidase on shear modulus of elasticity and surface viscosity of erythrocyte membrane [J]. Chinese Journal of Biomedical Engineering, 2001, 20(1): 33-37, 60.
[13] CHAMMAS P, EISENBERG S R. A microcontinuum model of electrokinetic coupling in the extracellular matrix: perturbation formulation and solution [J]. Journal of Colloid and Interface Science, 1994, 168(2): 526-538.
[14] 张玉亭, 吕彤. 胶体与界面化学 [M]. 北京: 中国纺织出版社, 2008: 179-183.
[15] 景允伸, 许宏, 常华, 等. 成核阶段对沉淀法白炭黑团聚程度的影响 [J]. 山东化工, 2015, 44(9): 28-32.
JING Yunshen, XU Hong, CHANG Hua, et al. The influence of the nucleation stage in precipitated silica preparation process on agglomeration degree of silica [J]. Shandong Chemical Industry, 2015, 44(9): 28-32.

