屏蔽数据并联系统的可靠性分析
师小琳,师义民,段俊杰
(1.西安邮电大学 电子工程学院, 陕西 西安 710121;2.西北工业大学 应用数学系, 陕西 西安 710072;3.西北大学 研究生院,陕西 西安 710069)
对于多个部件组成的系统,为了解系统的性能和可靠性指标,通常要对系统进行寿命试验。在理想状态下,试验不仅可以观测到系统的失效时间,还可以确定引起其失效的原因(即系统的失效是由哪一个部件失效而引起的)。然而对某些系统,由于其结构的复杂性以及试验经费、设备、技术等各种条件的限制,人们往往无法获知引起系统失效的确切部件,而只能将其失效原因归结为一些部件组成的集合,从而系统的失效原因就被屏蔽了。这种试验数据称为屏蔽数据,相应的系统称为屏蔽数据系统。近年来,关于屏蔽数据系统的可靠性分析已有较多研究成果。文献[1]首次在屏蔽数据下给出观测样本的似然函数,并利用极大似然估计法对指数部件的可靠性进行分析;Sarhan[2-3]分别讨论了串联系统中部件服从Weibull分布及几何分布时,部件参数和可靠性指标的极大似然估计和Bayes估计。Kuo等[4]基于屏蔽数据研究了威布尔部件串联系统中未知参数的极大似然估计(MLE)和Bayes估计(BE)。相关研究可参见文献[5-9]。
上述研究主要针对屏蔽数据串联系统。关于屏蔽数据并联系统的研究相对较少。文献[10-11]分别研究了广义指数分布、广义瑞利分布并联系统的可靠性分析。文献[12]研究了两部件并联系统中补充指数型分布参数的MLE与BE。相关的研究可见文献[13-14]。但是,在已有的文献中,关于屏蔽数据并联系统的研究是在完全样本或Ⅰ型、Ⅱ型截尾试验下完成的。与上述采样方式不同,逐步II型截尾试验允许在试验的不同阶段从试验中移走一些未失效的样品,以供研究产品的某些性能(例如退化性能)。这种截尾方式可用于缩短试验时间和保证一定量失效数据二者间的权衡。本文在逐步II型截尾试验下,研究补充指数分布三部件屏蔽数据并联系统的可靠性分析问题。讨论部件参数及可靠度函数的MLE和BE,并推导未知参数的最大后验密度置信区间。最后给出数值例子,对估计结果进行验证比较。
1 试验模型与似然函数

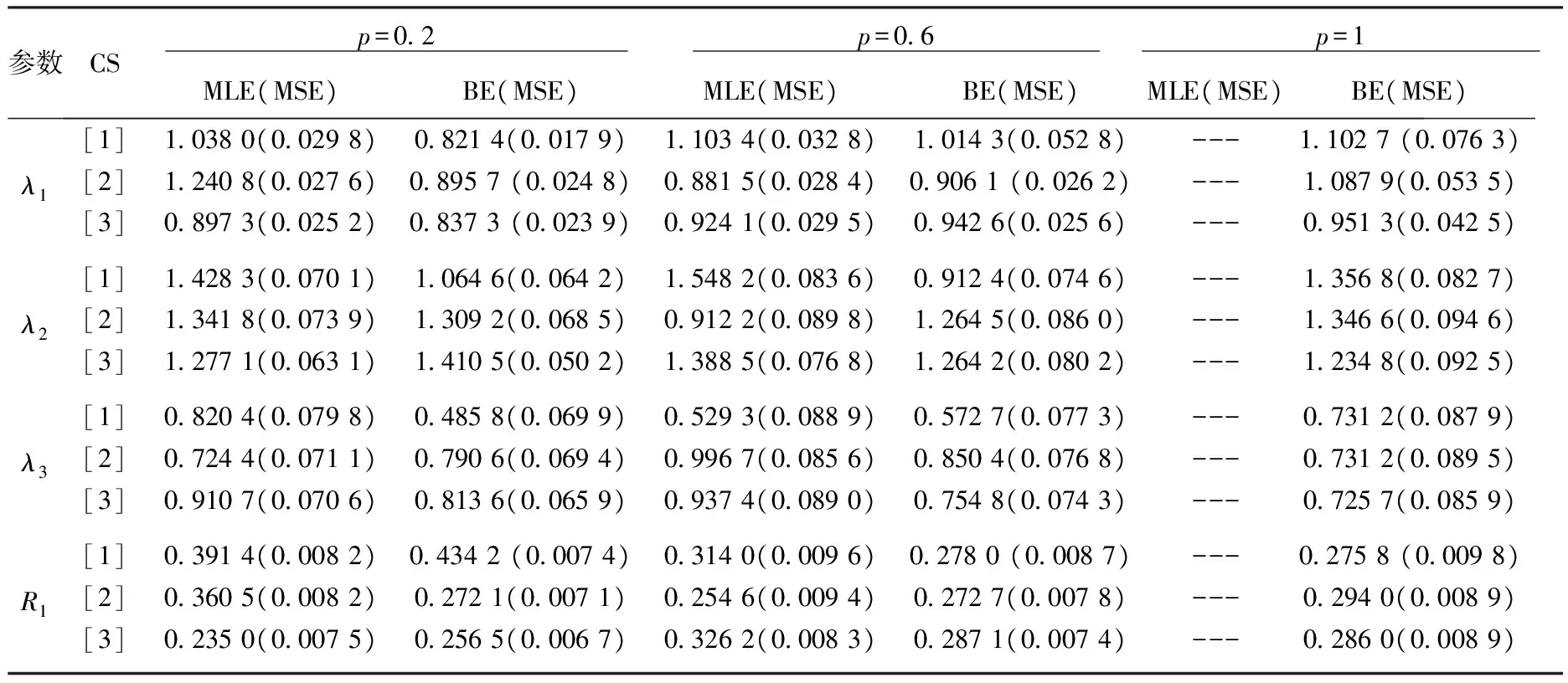
(T1,S1),(T2,S2),…,(Tm,Sm),m 对于上述试验,我们假设在同一时刻有且仅有一个系统失效,且屏蔽的发生与失效原因无关,即 P(Si=si|Ti=ti,Ki=j)= P(Si=si|Ti=ti,Ki=j′), ∀j,j′∈si,j≠j′ 若以随机变量Tij表示系统i中部件j的寿命,则Ti=max(Ti1,Ti2,…,TiJ),i=1,2,…,n,j=1,…,J。 根据上述假设,观测样本的似然函数可由下述定理给出。 定理1设并联系统中第j(j=1,…,J)个部件的密度函数和分布函数分别为fj(t),Fj(t),则在逐步Ⅱ型截尾试验下,观测样本的似然函数为 (1) 证明由文献[12]知,系统i的寿命Ti的密度函数为 在m个受试系统全部失效且试验中途无移走的情形下,样本的似然函数为 若有m个并联系统参与逐步II型截尾寿命试验,在第i个失效时刻Ti,从未失效系统中任意移走Ri个,则由文献[15]可得如下形式的似然函数 (2) 本文假设并联系统中各部件相互独立,第j(j=1,2,…,J)个部件的寿命服从参数为λj的补充指数分布,其概率密度函数与分布函数分别为: fj(t)=λjt-2exp{-λj/t},t>0,λj>0, (3) Fj(t)=exp{-λj/t},t>0,λj>0。 (4) 下面考虑3个部件组成的串联系统(J=3),我们以mj表示由于第j个部件失效而引发的系统失效个数, 即失效原因为部件集合Sj={j},j=1,2,3时系统的失效数;以m12,m13,m23,m123分别表示当失效原因为部件集合{1,2},{1,3},{2,3},{1,2,3}时系统的失效数。显然有 下面考虑并联系统中补充指数部件参数及可靠度函数的MLE。令λ=(λ1,λ2,λ3),将式(3),(4)代入式(1)中,即可得似然函数: (λ1+λ2)m12·(λ1+λ3)m13· (λ2+λ3)m23·(λ1+λ2+λ3)m123 (5) m12ln(λ1+λ2)+m13ln(λ1+λ3)+ 由此可得下列方程组: (6) 当系统的失效原因被完全屏蔽时无法得到极大似然估计。这时考虑部件参数及可靠度函数的贝叶斯估计。记|Ε|为集合E的元素个数。对于观测数据 D={(T1,S1),(T2,S2),…,(Tm,Sm)},记Aj={i||si|=1,Ki=j},j=1,2,3 以Sl分别表示屏蔽集{1,2}{1,3}{2,3}{1,2,3},记Ml={i||si|>1,si=Sl},l=1,2,3,4。此时似然函数可表示为 P(Ki=j|Ti=ti,Si=si)= (7) I(0,∞)(λj),j=1,2,3 I(0,∞)(λj)} (8) 利用贝叶斯公式及式(7) 及(8),可以得到λ的联合后验密度函数为 (9) 由于λ的联合后验密度函数计算复杂。故可应用Metropolis-Hastings(M-H)抽样算法[16]模拟参数(λ1,λ2,λ3)的后验样本。M-H算法计算步骤如下: 5)q=q+1; 并联系统部件j可靠度函数在时刻t的贝叶斯估计为 (j=1,2,3)。 对于给定的置信度1-α,从后验分布获得的置信区间不止一个,常用的方法是把α平分,用α/2和1-α/2分位数来获得λ1,λ2,λ3的置信区间,此即为实际中常用的等尾置信区间。但最理想的置信区间应是区间长度最短的,需要把具有最大后验密度的点都包含在区间内,而在区间外的点上的后验密度函数值不超过区间内的后验密度函数值。此时的区间称为最大后验密度(Highest posterior density,即HPD)置信区间[17]。 构造参数λ1,λ2,λ3的HPD置信区间的具体步骤如下: λj(1)≤λj(2)≤…≤λj(L),j=1,2,3; 3) 计算λ1,λ2,λ3的100(1-α)%置信区间,即[λj(q),λj(q+(1-α)*L)],j=1,2,3,;q=1,2,…,L-(1-α)L; 4) 在[λj(q),λj(q+(1-α)*L)],q=1,2,…,L-(1-α)L中寻找区间长度最短的区间,将其作为参数λj,的HPD置信区间(j=1,2,3)。 假定有60个完全相同的系统参加逐步II截尾寿命试验 (n=60), 每个系统由3个相互独立的部件并联而成。部件寿命分别服从参数为λ1=1,λ2=1.2,λ3=0.7的补充指数分布,并设定在第40个失效发生时停止试验,即m=40。试验中采用下列3种不同的逐步移走方案。 方案1:R1=R2=…=Rm-3=0,Rm-2=Rm-1=1,Rm=n-m-2; 方案2:R1=R2=…=0,Rm-3=n-m-2,Rm-2=0,Rm-1=Rm=1; 方案3:R1=R2=…=RK+1=1,RK+2=Rm-1=0,Rm=n-m-1-K。 其中K=[m/4]+1,[m/4]表示不超过m/4的最大整数。 重复上述模拟步骤2 000次,计算出部件参数及可靠度函数MLE的平均值(仍记为MLE),BE的平均值(仍记为BE)及相应的均方误差(MSE),并将上述计算结果列于表1中。均方误差的计算公式为 按照上一节给出的方法,在不同移走方案(CS)及屏蔽水平p下计算参数置信度为95%的HPD置信区间(HCI)、区间长度(CIL)及覆盖率(CP),并将计算结果列于表2中。 表1不同CS及屏蔽水平p下参数和可靠度函数的估计及均方误差(括号中为MSE, “---”表示无法计算) Tab.1Estimation and MSE of parameters and reliability functions for different CS and masking levelsp(The number in brackets is MSE,"---" means that it cannot be calculated) 参数CS p=02 p=06 p=1 MLE(MSE)BE(MSE)MLE(MSE)BE(MSE)MLE(MSE)BE(MSE)λ1[1]10380(00298)08214(00179)11034(00328)10143(00528)---11027(00763)[2]12408(00276)08957(00248)08815(00284)09061(00262)---10879(00535)[3]08973(00252)08373(00239)09241(00295)09426(00256)---09513(00425)λ2[1]14283(00701)10646(00642)15482(00836)09124(00746)---13568(00827)[2]13418(00739)13092(00685)09122(00898)12645(00860)---13466(00946)[3]12771(00631)14105(00502)13885(00768)12642(00802)---12348(00925)λ3[1]08204(00798)04858(00699)05293(00889)05727(00773)---07312(00879)[2]07244(00711)07906(00694)09967(00856)08504(00768)---07312(00895)[3]09107(00706)08136(00659)09374(00890)07548(00743)---07257(00859)R1[1]03914(00082)04342(00074)03140(00096)02780(00087)---02758(00098)[2]03605(00082)02721(00071)02546(00094)02727(00078)---02940(00089)[3]02350(00075)02565(00067)03262(00083)02871(00074)---02860(00089) 续表1 参数CS p=02 p=06 p=1 MLE(MSE)BE(MSE)MLE(MSE)BE(MSE)MLE(MSE)BE(MSE)R2[1]04111(00090)03380(00075)04034(00102)02516(00087)---03315(00095)[2]03505(00087)03364(00066)02642(00109)03249(00078)---03478(00085)[3]03547(00084)03631(00064)03705(00097)03173(00083)---03209(00097)R3[1]02491(00051)03126(00045)02619(00063)02378(00053)---02989(00076)[2]02345(00053)02207(00042)02827(00075)02179(00051)---02195(00075)[3]02718(00051)02408(00035)02684(00063)02161(00049)---02082(00068) 表2 不同CS及屏蔽水平p下参数95% 的HCI、区间长度(CIL)及覆盖率(CP)Tab.2 95% HCI,CIL and CP for different CS and masking levels p 由表1及表2中的数据可以看出: 1) 在相同屏蔽水平和移走方案下,Bayes估计的均方误差(MSE)较MLE的MSE小,故Bayes估计比MLE的精度更高。 2) 给定移走方案CS,屏蔽水平p越大,参数λ1,λ2,λ3及可度函数的MLE和BE的均方误差越大;给定屏蔽水平p,采用移走方案3时,参数λ1,λ2,λ3及可度函数的MLE和BE的MSE相对较小。采用移走方案1与2, 对参数及可度函数的MLE和BE的MSE无显著影响。 3) 当失效原因完全被屏蔽(p=1)时,无法计算参数λ1,λ2,λ3及可靠性指标的MLE,但可以获得其BE,且精度较高。 4) 从各置信区间的长度及覆盖率数据可以看出,各置信区间的覆盖率接近于0.95,覆盖率较大。随着屏蔽水平的提高,置信区间长度增加覆盖率减小。 本文研究了补充指数部件屏蔽数据并联系统的可靠性估计问题。基于逐步Ⅱ型截尾试验下屏蔽系统寿命数据,推导出试验样本的似然函数,进而获得了部件参数及可靠度函数的MLE与BE。在此基础上,利用M-H抽样算法给出了部件参数的最大后验密度置信区间。最后给出随机模拟例子,并计算出各种估计的均方误差及参数置信区间的长度及覆盖率,结果表明MLE和BE的均方误差都随屏蔽水平的增大而增大,且Bayes估计效果更优。 参考文献: [1]USHER J S, HODGSON T J.Maximum likelihood analysis of component reliability using masked system life data [J].IEEE Transactins on Reliability, 1988, 37(5):550-555. [2]SARHAN A M.Estimation of system components reliabilities using masked data [J].Applied Mathematics and Computation, 2003, 136:79-92. [3]SARHAN A M, KUNDU D.Bayes estimators for reliability measures in geometric distribution model using masked system life test data [J].Computational Statistics & Data Analysis, 2008, 52(4):1821-1836. [4]KUO L, YANG T Y. Bayesian reliability modeling for masked system lifetime data[J].Statistics & Probability Letters, 2000,47: 229-241. [5]SARHAN A M, KUNDU D. Bayes estimators for reliability measures in geometric distribution model using masked system life test data[J].Computational Statistics and Data Analysis, 2008,52(4):1821-1836. [6]SARHAN A M. Estimations of parameters in Pareto reliability model in the presence of masked data[J].Reliability Engineering and System Safety, 2003,82(1):75-83. [7]CAI J, SHI Y, LIU B. Inference for a series system with dependent masked data under progressively interval censoring[J].Journal of Applied Statistics, 2017, 44(1): 3-15. [8]FAN T H, HSU T M. Accelerated life tests of a series system with masked interval data under exponential lifetime distributions[J].IEEE Trans. on Reliability, 2012,61(3):798-808. [9]CAI J, SHI Y, YUE H. Accelerated life tests for Log-normal series system with dependent masked data under Type-I progressive hybrid censoring[J].Communications in Statistics-Simulation and Computation, 2017, 46(2):1628-1646. [10] ZHANG M, SHI Y, YANG Y. Reliability estimation for the generalized exponential components in parallel system using masked data[J].Information & Control, 2011, 40(4): 483-496. [11] GU X, SHI Y. Estimation of generalized rayleigh components reliability in a parallel system using dependent masked data [J].Journal of Physical Science, 2011, 15: 33-42. [12] AMMAR M, SARHAN A, AHMED H.Estimation of components reliability in a parallel system using masked system life data [J].Applied Mathematics and Computation, 2003, 138: 61-75. [13] XU X, WANG Y, WANG R, et al.Statistical analysis of parallel system for masked data under successive censored life test [J].Journal of Shanghai Normal University (Natural Sciences),2016,45(3):378-385. [14] XU X, WANG R, GU B.Statistical analysis of new model for masked data under parallel system [J].Journal of Sichuan Ordnance,2017,38(4)164-169. [15] 李凤,师义民,田亚爱.逐步增加II型截尾下Weibull分布的Bayes估计[J].工程数学学报, 2008, 25(4):641-650. [16] FAN T H,HSU T M. Accelerated life tests of a series system with masked interval data under exponentiallifetime distributions[J].IEEE Transactions on Reliability, 2012,61(3):798-803. [17] 茆诗松.贝叶斯统计[M].北京:中国统计出版社, 1999. [18] MUKHOPADHYAY C, BASU A P.Bayesian analysis of incomplete time and cause of failure data [J].Journal of Statistical Planning and Inference, 1997, 59: 79-100.
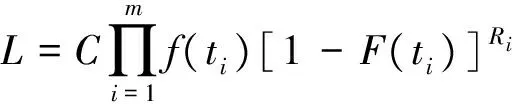
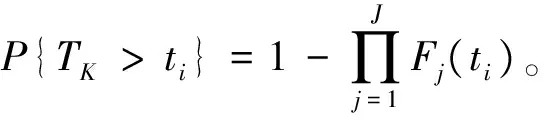
2 参数及可靠度函数的估计
2.1 极大似然估计
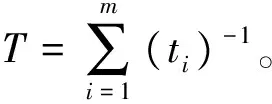
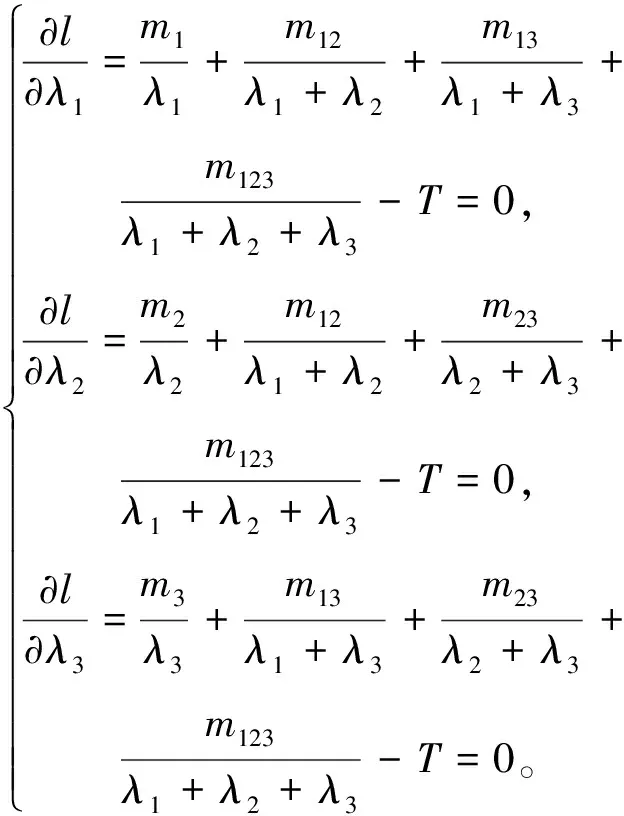

2.2 贝叶斯估计

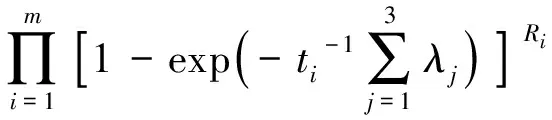

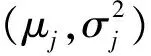
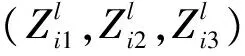



2.3 区间估计
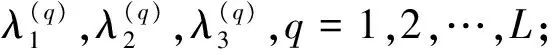
3 数值模拟



4 结 语

