分子模拟研究碳纳米管/聚合物纳米复合材料的黏弹性能*

胡利如，周桂桃，沈建祥**，李　雪，李海东

(1.嘉兴学院 材料与纺织工程学院，浙江 嘉兴 314001；2.嘉兴学院 南湖学院，浙江 嘉兴 314001)

聚合物纳米复合材料是通过将各种形状的纳米颗粒加入到聚合物基体中而获得的，具有优于纯聚合物的各种性能，如力学性能、光学性能、导热性能等。近年来，碳纳米管由于其独特的力学性能、电学性能受到了广泛的关注[1-2]。此外，碳纳米管也在其它领域显示了一定的应用潜力，包括节能、光学传感器、电场显示器、纳米半导体器件等。若要完全实现碳纳米管/聚合物纳米复合材料的性能，则必须要保证聚合物与碳纳米管的纳米复合。

在实际应用中，由于熵和焓的共同作用，很难实现无机碳纳米管在有机聚合物基体中均匀分散，往往有大量的聚集体形成。特别是当碳纳米管体积分数较大时，聚集体之间相互连接从而形成三维物理网络结构，这种物理网络结构对动态力学性能有显著的影响。例如，通过橡胶加工分析仪(RPA)进行动态剪切扫描，可以观察到材料的储能模量(G′)随着动态应变幅度的增加而呈现非线性减小，并且随着填料填充量的增加，非线性行为更加明显，该现象被称为Payne效应[3]。但是对于未填充的聚合物材料，其G′基本上不随应变幅度的增大而变化。聚合物纳米复合材料的Payne效应对于节省能源和保护环境都具有十分重要的意义，例如，降低材料的非线性行为可以减小汽车轮胎的滚动阻力，从而降低汽车在轮胎上的能量损耗。目前对于Payne效应的解释主要有以下几种观点：(1)认为Payne效应是填料纳米颗粒聚集体之间的相互连接在形变过程中的破坏所引起的，或者称为填料网络结构的破坏[4]；(2)认为Payne效应主要来自于填料周围形成的所谓聚合物玻璃化层[5]；(3)认为Payne效应是通过分子链段连接的长程填料网络结构破坏引起的[6]。直至目前，Payne效应机理依然处于争论之中。

由于分子模拟技术有可以对实验模型和实验中的各个参数进行定制的特点，近年来已经成为传统实验方法外的重要研究手段。但是，目前分子动力学模拟研究主要集中于复合体系的热力学与动力学、分子结构与活动性、分散与形貌以及静态力学行为等[7-8]，很少涉及材料的动态性能如Payne效应的模拟。Raos等[9]采用耗散粒子动力学模拟，研究了球形填料填充的聚合物纳米复合材料的 Payne 效应。Arya等[10]则采用分子动力学模拟，研究了表面接枝对于球形填料填充的聚合物纳米复合材料的黏弹性能的影响。然而，国内外关于碳纳米管/聚合物纳米复合材料的Payne效应的分子动力学模拟研究还很少。

本文采用分子动力学模拟方法对碳纳米管/聚合物纳米复合材料的Payne效应进行了研究。通过改变碳纳米管的长径比、含量以及其与聚合物基体之间的相容性等参数，希望寻找出有效调节与控制碳纳米管/聚合物纳米复合体系Payne效应的方法，为制备高性能聚合物纳米复合材料提供科学依据与理论指导。

1　模型与模拟方法

1.1　粗粒度模型

构建碳纳米管在聚合物基体中的粗粒度模型时，聚合物分子链采用Kremer和Grest的珠簧模型[11]。聚合物分子中每条链长30个珠子，每个珠子直径为1 σ，σ为长度的约化单位，也就是LJ势能的参数。虽然这些分子链比较短，但是已经表现出聚合物分子链的静态和动力学行为了。模型中的每个分子键对应于真实体系链骨架上的3～6个C—C化学共价键。

碳纳米管也采用珠簧模型，每个珠子直径为1 σ。在模拟中，碳纳米管长径比从10变化到18，如果把模拟中的粗粒度珠簧模型对应到真实体系，若设定单元结构的直径σ=2 nm(约为单壁碳纳米管的直径)，那么模拟应该可以对应单壁纳米短管填充的聚合物纳米复合材料，具体的模拟体系见表1。

表1　模拟体系参数

1.2　力场参数

聚合物分子链成键势能E计算公式如式(1)所示。

(1)

式中：k=30ε/σ2；R0=1.5σ；r为两个珠子之间的距离；σ为约化长度单位；ε为能量单位。聚合物分子链非成键珠子之间的相互作用采用Lennard-Jones势能Uij(r)计算，如式(2)所示。

(2)

式中：常数C用于保证势能函数Uij(r)为连续函数；ε=1.0；r为截断距离，设为2.5σ。

碳纳米管与碳纳米管、碳纳米管与聚合物之间的相互作用也都采用Lennard-Jones势能来表示，其中通过改变势能阱εnp来调节碳纳米管与聚合物基体之间的相容性。考虑到实际实验中可以通过加工工艺如强剪切流场等减少碳纳米管在聚合物基体中的团聚，因而在模拟体系中，碳纳米管与碳纳米管之间的相互作用设为排斥作用，即截断距离为1.12σ，如图1所示，图1中红色球表示碳纳米管，聚合物分子链未在图1中显示。从图1可以看出，碳纳米管在聚合物体系中基本没有团聚出现。

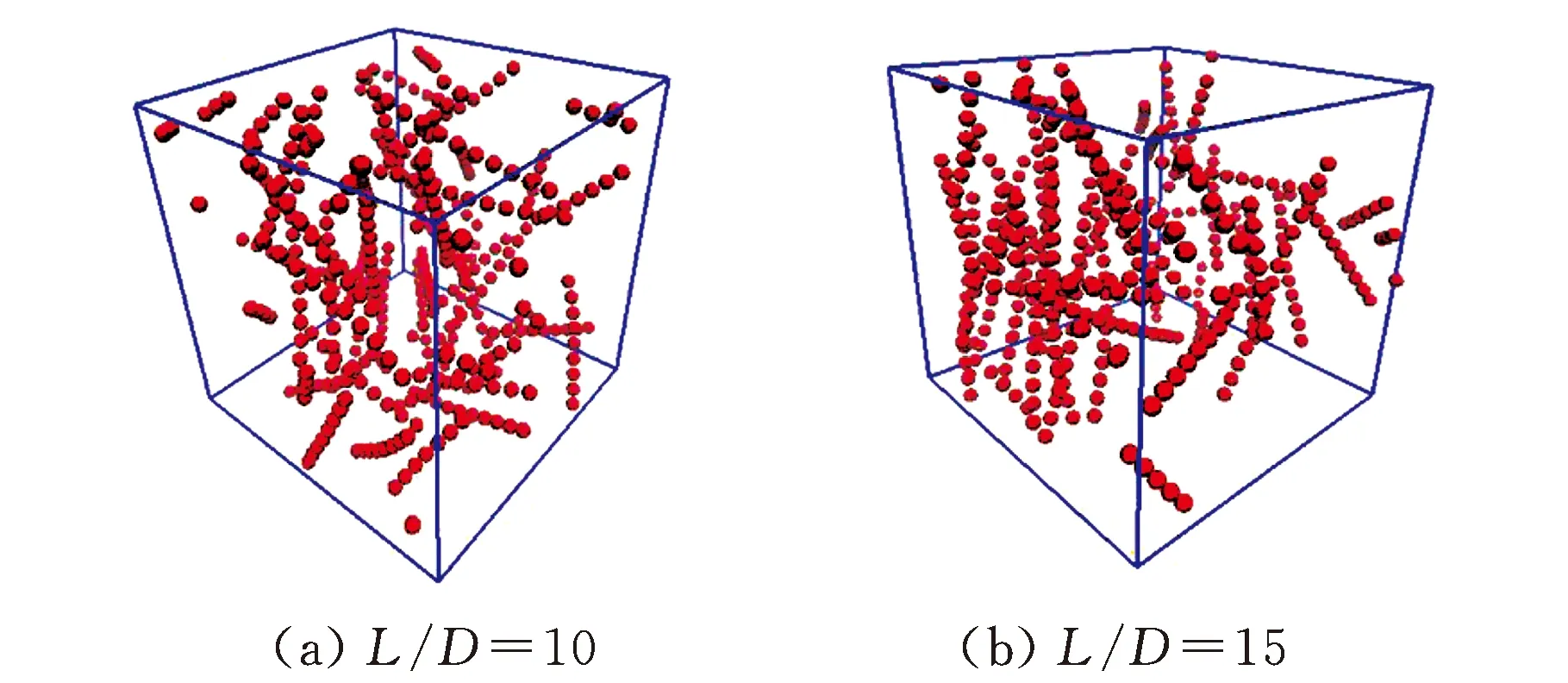
图1　不同长径比的碳纳米管模拟体系快照图

为保证碳纳米管的刚性，对碳纳米管上相邻的三个珠子加入了弯曲势能Ub(r)[12]，如式(3)所示。

Ub(r)=K(θ-θ0)

(3)

式中：K=500ε/rad2；θ0=π，即为180°；θ为连续3个珠子所形成的夹角。

1.3　动力学模拟

将所有的聚合物分子链和碳纳米管放置在一个非常大的模拟盒子中。首先，采用等温等压系综(NPT)，保持体系温度T*=1.0，压缩模拟体系使聚合物的密度ρ*=0.85。模拟盒子采用三维周期性边界条件。然后，采用等温等容系综(NVT)使模拟体系达到热力学平衡态，其中体系温度设为T*=1.0，高于聚合物的玻璃化转变温度。模拟体系达到平衡后，收集数据，并对数据进行分析。

采用SLLOD运动积分方程，对模拟体系进行非平衡态分子动力学模拟，实现周期性振荡剪切模拟。为实现模拟盒子剪切形变的模拟，采用 “Lees-Edwards”边界条件[13]。

在周期性剪切过程中，剪切应变是时间的正弦函数，如式(4)所示。

γ(t)=γ0sin(2πvt)

(4)

式中：γ0为最大剪切应变振幅；v为剪切频率；γ(t)为即时剪切形变；t为剪切的施加时间。

模拟中，固定剪切频率为v=0.01τ-1，考察了模量随剪切振幅的变化情况。剪切应力应为滞后的正弦函数，如式(5)所示。

σ(t)=σ0sin(2πvt+δ)=σ′sin(2πvt)+

σ″cos(2πvt)

(5)

式中：δ为损耗角；σ0为最大剪切应力振幅；σ(t)为即时剪切应力；v为剪切频率；t为剪切的施加时间；σ′和σ″分别为复模量的同相分量和非同相分量。G′、损耗模量(G″)、损耗因子(tanδ)的计算如式(6)～式(8)所示。

G′=σ′/γ0

(6)

G″=σ″/γ0

(7)

tanδ=G″/G′=σ″/σ′

(8)

实验中所有的分子动力学模拟均在Sandia National Laboratories开发的大尺度原子/分子大规模并行模拟器(LAMMPS)[14]中运行。

2　结果与讨论

2.1　碳纳米管的长径比对Payne效应的影响

设定碳纳米管的长径比从10变化到18，碳纳米管质量分数为7.0%，碳纳米管与聚合物基体之间的相互作用参数εnp=1.0，研究了碳纳米管的长径比对聚合物纳米复合材料Payne效应的影响，如图2所示。

图2(a)显示了碳纳米管的长径比对G′的影响。对于一个碳纳米管填充的模拟体系，随着剪切振幅γ0的增加，其G′都有所下降，这种G′对剪切振幅的依赖性就是所谓的Payne效应。G′随着剪切振幅的下降程度越大，Payne效应越显著。从图2(a)可以看到，随着碳纳米管长径比降低，材料的Payne效应有所下降，这与实验观察到的现象一致[15]。在碳纳米管与聚合物基体界面上，聚合物分子链的活动性往往会受到碳纳米管的影响而减弱，形成所谓的“聚合物壳层”。因此，Payne效应随着碳纳米管长径比的下降而降低，原因是碳纳米管长度降低的同时颗粒数量增加，相互之间距离更为均匀，分散状态更好，碳纳米管之间通过表面“聚合物壳层”相连的局部网络结构也越弱。此外，在同等剪切振幅下，G′随着碳纳米管长径比的增加而增加，这意味着材料的增强效果也更好。

γ0(a)

γ0(b)图2　碳纳米管长径比对聚合物纳米复合材料黏弹性能的影响

碳纳米管长径比对材料的损耗因子tanδ的影响如图2(b)所示。在模拟体系中，由于碳纳米管基本没有团聚，故聚合物纳米复合材料的内耗主要来自于聚合物基体的滞后损失。从图2(b)可以看出，随着碳纳米管长径比的增加，材料的损耗因子有所下降，表明长径比大的碳纳米管对聚合物分子链的影响更大，使聚合物分子链的弹性响应更为明显。但是，在较大尺度下，聚合物分子链则主要体现为黏性响应，因此在最大剪切振幅γ0≥0.5的情况下，不同长径比对应的聚合物纳米复合材料的损耗因子都有所增加。

2.2　碳纳米管含量对Payne效应的影响

碳纳米管含量对聚合物纳米复合材料黏弹性能的影响如图3所示，碳纳米管长径比固定为15，碳纳米管与聚合物基体之间的相互作用参数设为εnp=1.0。

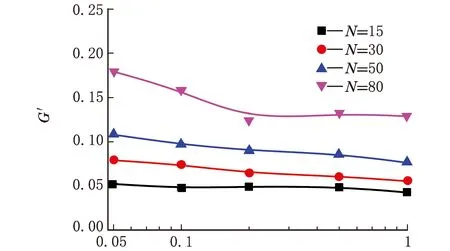
γ0(a)

γ0(b)图3　碳纳米管含量对聚合物纳米复合材料黏弹性能的影响

从图3(a)可以看出，即使碳纳米管没有团聚，随着碳纳米管含量的增加，材料的Payne效应也显著提高。这是因为随着碳纳米管数目的增加，碳纳米管之间的平均距离缩短，通过表面的“聚合物壳层”连接的局部网络结构也越强。另外，在同等剪切振幅下，G′随着碳纳米管含量的增加而增加，意味着材料的增强效果也越好。从图3(b)可以看出，由于碳纳米管基本没有团聚，所以随着碳纳米管含量的增加，碳纳米管与聚合物基体之间的接触面也越大，使得更多的聚合物分子链受到碳纳米管的影响而具有更大的弹性响应。类似地，由于聚合物分子链在大剪切振幅情况下(γ0≥0.5)的流体动力学效应，使得聚合物纳米复合材料的损耗因子大大增加。

2.3　碳纳米管与聚合物基体之间的相容性对Payne效应的影响

碳纳米管与聚合物基体之间的相容性对聚合物纳米复合材料G′的影响如图4所示，固定碳纳米管长径比为15，碳纳米管数目为30根，碳纳米管与聚合物基体之间的相互作用参数εnp从1.0变化到12.0。

γ0图4　碳纳米管与聚合物基体之间的相容性对聚合物纳米复合材料储能模量的影响

从图4可以看出，碳纳米管与聚合物基体之间的相容性越好，在同等剪切振幅下的G′就越大，即聚合物纳米复合材料的增强效果就越好。然而，碳纳米管与聚合物基体之间的相容性增加，材料的Payne效应也随之增加。这是因为，随着碳纳米管与聚合物基体之间相互作用的增加，碳纳米管之间通过共同吸附分子链而形成局部聚集[16]，这种局部网络会随着剪切振幅的增加而被破坏得更严重，导致聚合物纳米复合材料的G′下降，其强度则会随着碳纳米管与聚合物基体之间相互作用的增加而增加，从而导致Payne效应更加显著。碳纳米管这种局部聚集的现象可由图5观察到，图5中红色球表示碳纳米管，聚合物分子链未在图5中显示。

3　结　论

(1) 建立了碳纳米管/聚合物纳米复合材料的粗粒度模型，通过分子动力学模拟计算，得到了材料的黏弹性能。并用模拟体系的快照图表征了碳纳米管在聚合物基体中的分散情况。

(2) 随着碳纳米管长径比和碳纳米管含量的增加，碳纳米管/聚合物纳米复合材料的增强效果越来越好，但是复合材料的Payne效应也更显著。

(3) 当碳纳米管在聚合物基体中基本不出现团聚的情况下，随着碳纳米管与聚合物基体之间的相互作用越强(相容性越好)，碳纳米管/聚合物纳米复合材料的Payne效应也越显著。

参考文献：

[1]COLEMAN J N,KHAN U,BLAU W J,et al.Small but strong：a review of the mechanical properties of carbon nanotube-polymer composites[J].Carbon,2006,44(9)：1624-1652.

[2]SPITALSKY Z,TASIS D,PAPAGELIS K,et al.Carbon nanotube-polymer composites：chemistry,processing,mechanical and electrical properties[J].Progress in Polymer Science,2010,35(3)：357-401.

[3]BOKOBZA L.Multiwall carbon nanotube elastomeric composites：a review[J].Polymer,2007,48(17)：4907-4920.

[4]WANG M J.The role of filler networking in dynamic properties of filled rubber[J].Rubber Chemistry and Technology,1999,72(2)：430-448.

[5]PAPON A,MONTES H,HANAFI M,et al.Glass-transition temperature gradient in nanocomposites：evidence from nuclear magnetic resonance and differential scanning calorimetry[J].Physical Review Letters,2012,108(6)：065702.

[6]ZHU Z,THOMPSON T,WANG S Q,et al.Investigating linear and nonlinear viscoelastic behavior using model silica-particle-filled polybutadiene[J].Macromolecules,2005,38(21)：8816-8824.

[7]ALLEGRA G,RAOS G,VACATELLO M.Theories and simulations of polymer-based nanocomposites：from chain statistics to reinforcement[J].Progress in Polymer Science,2008,33(7)：683-731.

[8]YAGYU H,UTSUMI T.Coarse-grained molecular dynamics simulation of nanofilled crosslinked rubber[J].Computational Materials Science,2009,46(2)：286-292.

[9]RAOS G,CASALEGNO M.Nonequilibrium simulations of filled polymer networks：Searching for the origins of reinforcement and nonlinearity[J].The Journal of Chemical Physics,2011,134(5)：054902.

[10] HATTEMER G D,ARYA G.Viscoelastic properties of polymer-Grafted nanoparticle composites from molecular dynamics simulations[J].Macromolecules,2015,48(4)：1240-1255.

[11] KREMER K,GREST G S.Dynamics of entangled linear polymer melts：A molecular-dynamics simulation[J].The Journal of Chemical Physics,1990,92(8)：5057-5086.

[12] SHEN J,LI X,SHEN X,et al.Insight into the dispersion mechanism of polymer-grafted nanorods in polymer nanocomposites：A molecular dynamics simulation study[J].Macromolecules,2017,50(2)：687-699.

[13] LEES A W,EDWARDS S F.The computer study of transport processes under extreme conditions[J].Journal of Physics C：Solid State Physics,1972,5(15)：1921-1928.

[14] PLIMPTON S.Fast parallel algorithms for short-range molecular dynamics[J].Journal of Computational Physics,1995,117：1-19.

[15] 李芬.碳纳米管橡胶纳米复合材料的制备与性能[D].北京：北京化工大学,2013.

[16] LIU J,GAO Y,ZHANG L,et al.Nanoparticle dispersion and aggregation in polymer nanocomposites：a molecular dynamics simulation[J].Langmuir,2011,27(12)：7926-7933.