基于SIFT的无人机航拍图像快速拼接技术研究

宋建辉　闫蓓蕾

(沈阳理工大学自动化与电气工程学院　辽宁 沈阳 110168)

0　引　言

近年来基于无人飞行器获取遥感图像的配准和拼接技术，大致分为基于参考图像以及基于无人机飞行姿态参数两种方法。基于无人机飞行姿态参数的方法能够实时地校正由于无人机飞行姿态的改变、高度变化而产生的图像几何畸变问题。但是在实际执行任务过程中，无人机飞行姿态比较容易受外部环境干扰的影响，从而会产生飞行姿态参数获取不准确、不及时等问题[1]。而基于参考图像的算法不会受到传感器各项参数、无人机周围环境等因素的影响，对获取的图像能够迅速完成配准和拼接工作，所以采用参考图像的算法在配准和拼接研究中获得了普遍应用[2]。

参考图像的匹配方法，将图像上检测得到的部分特征当作配准基元，主要分为图像特征配准以及区域配准两大类别。用来匹配的关键元素有点、线、区域或者一些具有特殊结构的元素。而图像的点特征有旋转、平移不变的特性，并且稳定性高、配准精度高、运算的速度快[3]，于是，利用图像中的特征点来实现配准和拼接，是如今应用最广泛的方法[4]。

Harris角点检测算子计算量少，可以稳定处理图像的方向变化、灰度的改变等问题[5]。然而该提取算法无法实现尺度不变性，对那些存在较明显仿射变换的图像，配准效果有所欠缺[6]。SIFT算法是一种选择与描述图像特征的方法，能够解决图像在方向及角度变化、缩放改变、平行移动、明暗改变等状态下的特征匹配。为了使拼接结果更准确，本文选用SIFT算法。

将SIFT特征提取算法单独应用于图像匹配工作中，会占用过多的运算时间，而且对于处理大图像的效果较差。针对匹配速率问题，本文对图像匹配进行了改进，在匹配算法中加入了SSDA算法，缩短了图像特征点匹配时间，大大提高了匹配效率。然后利用RANSAC算法求取匹配点的转换矩阵，并将特征点对进行准确配准，该方法具有鲁棒性，最终完成图像拼接工作。

1　基于特征点的图像拼接算法

1.1　SIFT特征提取算法

SIFT特征向量的生成步骤如图1所示。

图1SIFT特征向量的生成步骤

1.1.1尺度空间极值检测

Witkin在1983年提出尺度空间理论，该理论作为检测不变特征的基础，主要解决了一维信号平滑处理问题。次年，Koenderink又把该理论扩展到了二维图像，而且他论证了高斯卷积核是唯一能够处理尺度变换的变换核[7]。

二维图像可以由图像以及高斯核卷积得出位于多种尺度下的尺度空间[8]：

L(x,y,σ)=G(x,y,σ)*I(x,y)

(1)

式中：G(x,y,σ)是高斯核函数：

(2)

式中:I(x，y)是图像数据；(x，y)是图像点的像素坐标值；σ是高斯正态分布的方差；L(x,y,σ)就是所求得的图像的尺度空间。

Lowe应用尺度空间的差分高斯DoG极值作为其判断依据，解决了在尺度空间提取出可靠关键点的问题。DoG算子是相异尺度高斯核的差分，规定如下：

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)=

L(x,y,kσ)-L(x,y,σ)

(3)

式中：k是两个相邻尺度间的比例影响参数。

1.1.2确定关键点的位置及尺度

经过三维二次函数的拟合使选取点的坐标值更准确，来获得原始图像的SIFT候选关键点集。但是该点集中，还包含一些对噪声较为敏感或者对比度较低的点，以及处于图像边缘而很难精确获取其位置的点，如果要实现SIFT特征点的稳定性，就一定要把上述点排除。

1.1.3确定关键点方向

确定特征点的方向后，特征描述符才能够以和方向相关的方式表示，这样SIFT算子就不会受到旋转变化的影响。根据关键点邻域像素的梯度分布特点来确定其方向。对于每幅高斯图像，每一个关键点L(x,y)的梯度分布的模m(x,y)及方向θ(x,y)都可以由以下公式得出：

m(x,y)=

(4)

(5)

式中：L(x,y)所表示的尺度是关键点所在尺度。

此时，提取点的检测任务已经结束，其中，每个提取点显示3个信息：尺度、坐标、方向。

1.1.4特征向量生成

为了提高选取点配准的稳定性，将每个点通过4×4，一共16个种子点表示，每个点包含128个数据[9]，结果表示的SIFT特征向量为128维。如此，就生成了图像特征描述符用以图像特征匹配，该SIFT特征向量不再受到方向、角度改变等干扰。

1.2　SSDA算法

1972年,Bamea D I及Silverman H F等提出了SSDA算法，并将其应用到图像匹配算法中。SSDA算法通过设定阈值，使模板在搜索图像上进行搜索[10]，可以快速排除发生误匹配的点，使配准算法更简单易行，因此使得配准速度得到很大提升。

SSDA算法过程如下：

目标图像S设为N×N，待配准图像T设为M×M，将待配准图像叠放在目标图像上进行平移。平移待配准图像的过程中其下的目标图像区域设作子图Si,j，在目标图像中Si,j左上部分的点的坐标值为(m,n)，即待匹配图像上的每个像素点坐标值[11]，其中：1≤i,j≤N-M+1且0≤m,n≤M。

(1) 计算绝对误差值：

ε(i,j,mk,nk)=

(6)

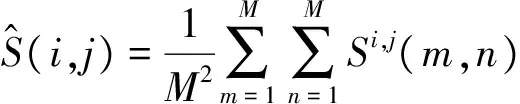
(2) 确定一个不变阈值Tk。

(3) 在Si,j(m,n)中，随机选择一个像点(mk,nk)，并求出它和待匹配图像上相应点的绝对误差值ε(i,j,mk,nk)，之后将这个ε值和其余匹配点对的ε值累加，当累加至r次的ε值超过Tk后，就不再对该目标模块进行累加运算，同时把Si,j(m,n)平移至下一处位置，并记下次数r。定义SSDA的检测曲面为：

(7)

(4) 通过对比，匹配点就是取值最大的I(i,j)指向的像素点(i,j)。

1.3　RANSAC匹配算法

RANSAC匹配算法用于解决关键点匹配错误问题[12]。该方法具有很好的鲁棒性及容错性质。其核心思想是：在未知的函数模型参数中及未知的数据集中进行鲁棒性拟合。首先设计一个目标参考模型，然后利用重复采样技术计算出一个最小点集合，在此集合中估算出目标模型所需要确定的参数；再利用已经解算出的初始参数值把原始数据集分割成内点(即符合目标函数的点)与外点(即与目标函数不相符合的点)；最后依据所获得的内点来重新求取目标模型的参数值[13]。

运用RANSAC来求取匹配点的变换矩阵，其过程如下：

(1) 计算图像间的变换矩阵的初始值：

① 随机从获取的配准特征点中抽取4组点对作为一组实验数据，并计算变换矩阵H[14]。

② 计算每组对应点的距离d。

③ 计算与H一致的内点数。

④ 找出含有内点数量最大的H，当数量一样时，找出最小的内点标准方差对应的H值。

假设图像序列之间的变换是投影变换：

(8)

式中：H的自由度是8。假设p=(x,y)，q=(x′,y′)是一组匹配的特征点对，则根据投影的变换公式：

(9)

可以选用4个最优的匹配点对求取H中包含的8个自由度参数hi(i=0,1,…,7)，并以此作为H的初始值。

(2) 迭代精炼变换矩阵H：利用包含内点的全部匹配再次计算H。

(3) 引导匹配：使用估计所得的H定义对极线附近的搜寻区域，并进一步确定特征点的相应关系。

(4) 反复迭代(2)、(3)步骤，一直到对应点的数目稳定以结束计算。

2　图像融合

根据求得的转换矩阵H，对图像作转换处理来确定图像间的相同区域，然后把待融合的图像映射到一张新图像中作为拼接图。

本文选用加权平滑算法来处理图像拼接缝问题。由图2可知，将两幅待拼接图像中相应点的像素灰度值P_L与P_R作加权平均运算可求出图像交叠范围内像素点的灰度值P[15]，即：

P=k×P_L+(1-k)×P_R

(10)

式中:k为可调因子。一般情况下，0

图像1 图像2

拼接图像

图2加权平滑算法

3　实验结果与分析

本文使用Intel(R) Core(TM) i3-3110M处理器，并用MATLAB仿真软件，选用大量图像来验证上述算法的可行性。下面列举两组实验结果。

首先将Harris角点检测算法、SIFT特征提取算法比较，通过这两种方法所获得的匹配特征点对数如表1所示。

表1　Harris与SIFT实验对比表

由表1可以看出，SIFT特征提取算法比Harris角点提取算法所得到的关键点匹配对数高出几倍，这就证明基于尺度不变特征提取算法的图像拼接的精度更高，拼接的结果图配准完善度更好。

将SIFT配准算法、SIFT+SSDA配准算法作比较，选用包含不同关键点数的图像进行匹配，配准所用时间见表2，对比结果体现出SIFT+SSDA算法的高效率性。

表2　匹配算法时间比较

通过分析以上两组对比实验，本文将SIFT特征提取算法、SSDA算法和RANSAC精确匹配算法相结合，得到如图3-图7的拼接效果图。分别列举了SIFT特征点提取、SSDA初步配准、RANSAC精确配准以及无缝拼接结果图。

左图右图图3　原图

图4　SIFT特征点提取

图5　SSDA初步配准结果图

图6　RANSAC精确配准结果图

图7　图像拼接结果图

图4中显示出图像的所有SIFT特征点；图5中添加SSDA算法来对图像进行初步配准，虽然提高了配准速率，但存在少量误匹配点；图6中利用RANSAC算法进行精确匹配，其上线段为各组匹配点对的连线，每条线段互相平行，匹配精度较高；图7中的图像未产生明显的拼接痕迹，而且也拓宽了单幅图像的场景视野。

由于SIFT算法能够解决图像在出现平移、方向及角度改变等状态下的特征匹配问题，本文根据该特点将其中一幅图像分别旋转90度、缩小尺寸，经过实验仿真，依旧能够获得图7的拼接结果，匹配结果见图8、图9。

图8　旋转90度RANSAC精确配准结果图

图9　缩小尺寸RANSAC精确配准结果图

4　结　语

由于SIFT算法能够解决图像平移、方向及角度改变、光照改变等问题，无人飞行器在不同时间、以不同角度拍摄两幅或者多幅含有重叠区域的图像后，依旧可以获得较好的拼接效果，这样就降低了无人飞行器工作时间和地点的局限性。利用SIFT算法选取特征点，然后在图像配准中添加SSDA算法，再根据RANSAC进行精确匹配，如此，缩短了配准时间，提升了匹配速度，并使图像的匹配度更高，拼接效果更完善。但是，本文算法仍存在不足之处：由图8、图9可以看出，当图像发生尺度改变、旋转等变化时，匹配点对数会略微减少，继而会影响拼接效果，有待改进。

[1] 周志艳，闫梦璐，陈盛德，等.Harris角点自适应检测的水稻低空遥感图像配准与拼接算法[J].农业工程学报，2015,31(14)：186-193.

[2] 赵芹，周涛，舒勤.基于特征点的图像配准技术探讨[J].红外技术，2006,28(6):327-330.

[3] 刘晓龙，李英成.基于多源遥感影像融合的影像匹配技术[J].测绘科学，2007,32(3):59-61.

[4] 赵前鑫，杨英宝.一种基于角点特征的遥感影像自动配准方法[J].测绘科学，2013,38(3):160-162.

[5] 郭翠翠.基于并联机构的三维视觉重构系统标定技术研究[D].燕山大学，2009.

[6] 袁杰.基于SIFT的图像配准与拼接技术研究[D].南京理工大学，2013.

[7] 赵小川.MATLAB图像处理—能力提高与应用案例[M].北京航空航天大学出版社，2014.

[8] 郭海礁.常用图像拼接算法综述[J].科技信息，2012(7):475-476.

[9] 李晓静, 赵蕾, 刘婷婷. 基于SIFT特征的遥感图像配准方法研究与实现[J]. 电脑编程技巧与维护, 2012(8):106-107,151.

[10] 王昌诚.现代图像处理技术在深海高清图像分析中的研究[D].青岛科技大学,2015.

[11] 谢昕，徐殷，熊焕东，等.基于压缩感知的SIFT图像匹配算法研究[J].华东交通大学学报,2015,32(6):115-121.

[12] 李明.一种焊缝成形形貌的视觉评判方法研究[D].兰州理工大学，2014.

[13] 任宇琪. 面向空间非合作目标捕获的位姿测量方法研究[D].哈尔滨工业大学，2015.

[14] Zitova B, Flusser J. Image registration methods: a survey[J]. Image and Vision Computing,2003,21(11):977-1000.

[15] 刘志伟, 高军, 张明. 机载红外搜救系统中的图像快速拼接[J]. 计算机系统应用, 2015, 24(2):189-194.