一种基于市场真实情况的ATM选址模型的研究及应用
周继恩 冯 兴 冯 鑫
(中国银联股份有限公司 上海 201201)
0 引 言
随着社会经济的不断发展,自动取款机ATM已经成为人们经济生活中不可或缺的重要基础设施之一。对银行而言,合理的ATM部署不仅能够提升银行客户的用户体验,而且能够帮助银行在激烈的行业竞争中发掘潜在客户和提高市场份额。设施区位问题是关于设施在空间最优化布局的区位分析问题。基本的设施区位问题考虑在离散空间中放置P个设施以服务D个需求点,并根据实际问题提出不同的优化目标获得不同的模型,如P-Meidan[1]问题中的minisum模型考虑最小化需求点与其最近设施点的加权距离和,其中权重为该需求点的需求值。minimax模型[2]考虑最小化所有需求点与其最近设施点的距离的最大值。ATM选址可以被视为一种特定的设施区位问题,但由于ATM市场情况高度复杂,ATM的部署受到人口密度、商业因素、竞争因素和已部署机具等多方面影响。经典的设施区位问题由于其数学模型的抽象性,无法适用于ATM选址问题。本文提出一种更加适用于ATM选址的P-Median问题的一种变形,设计了基于Voronoi图和修改的K中心点聚类的求解算法,构建了更加符合市场真实情况的ATM选址模型,并以深圳市某银行为例,应用模型获得ATM的合理部署位置。
1 P-Median问题与ATM选址原则
P-Median问题是一个经典的设施区位问题,由Hakimi[1]在其影响深远的工作中提出。P-Median问题考虑在离散空间中部署P个设施,使得空间中需求点与其距离最近的设施的加权距离和最小,需求点的权重为其需求值。从定性的角度来看,P-Median问题试图使所放置的P个设施尽量靠近空间中的需求点。Kariv等[3]证明在一般的图结构中,P-Median问题是一个NP难的问题。因此P-Median问题的求解通常使用近似或启发式算法[4]。P-Median问题是设施区位问题的核心,很多现实生活中的设施区位问题都可以转化成为P-Median问题。
与P-Median问题相似,ATM选址的一个原则同样是试图让ATM尽可能靠近用户。但ATM选址问题难以直接转化为P-Median问题,原因如下:
1) P-Median问题及其他经典设施区位问题通常考虑在空白的空间中投放设施,即研究区域中无已部署设施。对于ATM选址而言,由于市场中已经存在大量ATM且ATM的部署与裁撤具有较高的成本,空白区域假设不适用。
2) P-Median问题不考虑空间中同类设施的竞争影响,而ATM市场则是一个高度竞争的市场,ATM选址模型须考虑竞争因素。
3) 在P-Median问题及其他经典设施区位问题中,空间中的需求点和其需求值大小通常为已知固定值。ATM选址问题中,用户的位置与其需求值大小比较模糊,需要首先对需求点进行筛选并评估需求值。
ATM选址是一个复杂的商业决策过程,影响ATM部署合理性的因素非常多,各个因素之间的相互关系也非常复杂。为了使问题更加清晰,本文遵循以下几点假设:
1) ATM市场为竞争市场,即市场中包含多家银行的ATM。
2) 用户优先考虑使用与自身距离最近及与其持有银行卡相同开户行名称的ATM,否则跨行取款需付手续费。
3) 各个银行的持卡人均匀分布于市场中,即在空间中每一个子区域内各银行的持卡人数比例与空间整体各银行的持卡人数比例相同。
2 ATM选址模型定义
本文提出一种基于P-Median问题的ATM选址模型,模型具有一个研究主体B银行(如无特殊说明,后文使用B银行代表模型研究主体)。为符合市场实际情况,模型加入多银行竞争因素并在已有ATM的基础上在空间中选取P个B银行ATM部署地点,使得空间中的需求点与其距离最近的B银行ATM加权距离和最小,其中权重为需求值。
2.1 需求与竞争因素评估
影响ATM选址的因素很多,包括研究区域的GDP、人口密度、公共设施分布、商圈分布等[5]。建立ATM选址模型需要首先对研究区域从空间因素和经济因素等方面进行考察[6],筛选需求点,评估需求值。一般而言,ATM的交易量与其地理位置的人流量成正比,因为用户通常在出行途中使用ATM。基于此,本文选取需求点类型包括:小区、写字楼、商圈、科技工业园区、机场、火车站、地铁站。不同的需求点通常具有不同的需求值,基于模糊综合评判方法[7],本文使用需求点的类型因子和规模因子对需求值进行评估。类型因子即需求点所属类型的权重值,规模因子即评价同类需求点的规模大小因子值,类型因子与规模因子的乘积为需求点最终的需求值。各个需求点的类型因子和规模因子通过分析ATM的交易数据获得,结果如表1所示。
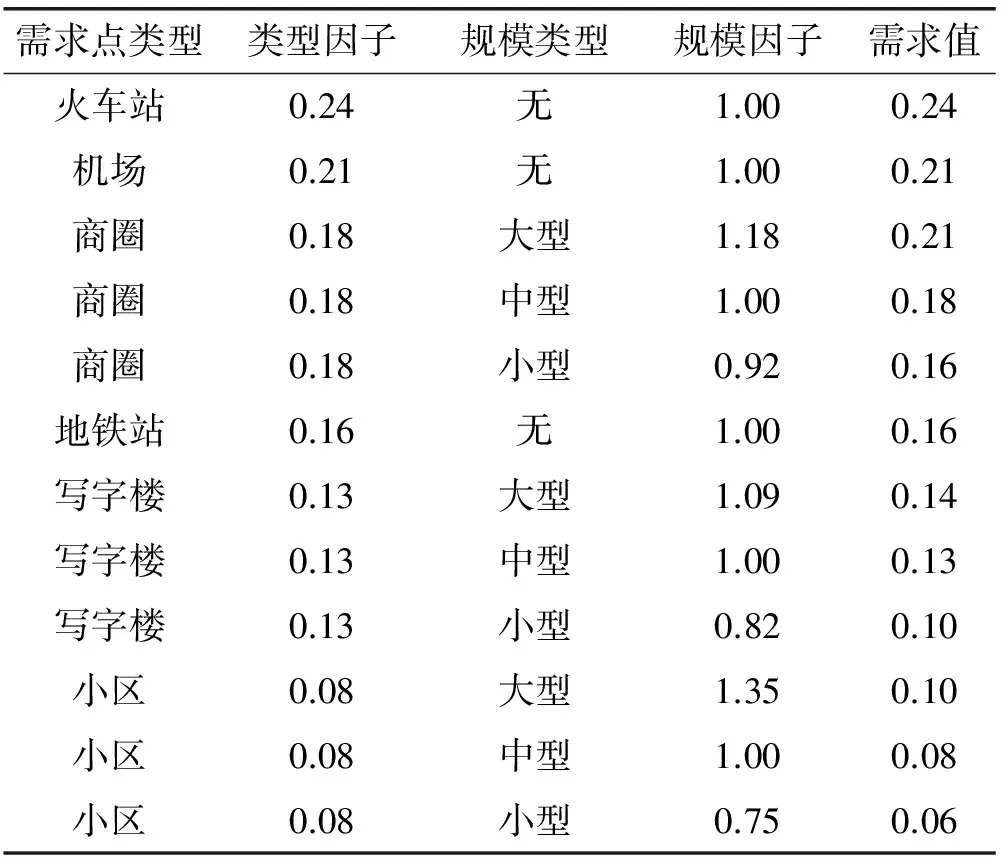
表1 ATM选址需求点需求值评估
由于城市的小区、地铁站等通常较多,易导致研究区域需求点过于密集,为了提高模型的计算效率,在实际的模型计算中首先对选取的需求点进行合并。由于不同的需求点类型权重不同,本文对距离500米以内的同类型需求点进行合并。
基于假设1,在建立ATM选址模型时须考虑竞争因素。由于市场中通常有多家银行,为使问题清晰,除研究主体B银行外,市场中其他银行的ATM均视为竞争点。通常,各个银行的发卡量不同,基于假设2,不同银行在市场中竞争影响大小并不相同。基于假设3,为对不同银行的ATM竞争影响进行评估,本文使用研究区域内某一银行在中国银联跨行转接交易中的银行卡交易活跃程度作为该银行ATM的竞争影响权重。
2.2 Voronoi图与空间划分
本文使用2维的Voronoi图[8],以B银行ATM为生成元构建ATM实施部署的拓扑结构平面图,并为需求点和竞争点快速确认距离其最近的B银行ATM。Voronoi图是一种平面分割方法,其使用N个生成元将平面划分为N个区域,每个区域仅存在1个生成元,并使得每个区域中的点到该区域中生成元的距离比到其他生成元距离更近。Voronoi图的示例见图1,其数学定义如公式所示:
在距离空间(X,d)中有n个点s1,s2,…,sn, 将X划分为n个区域使得:
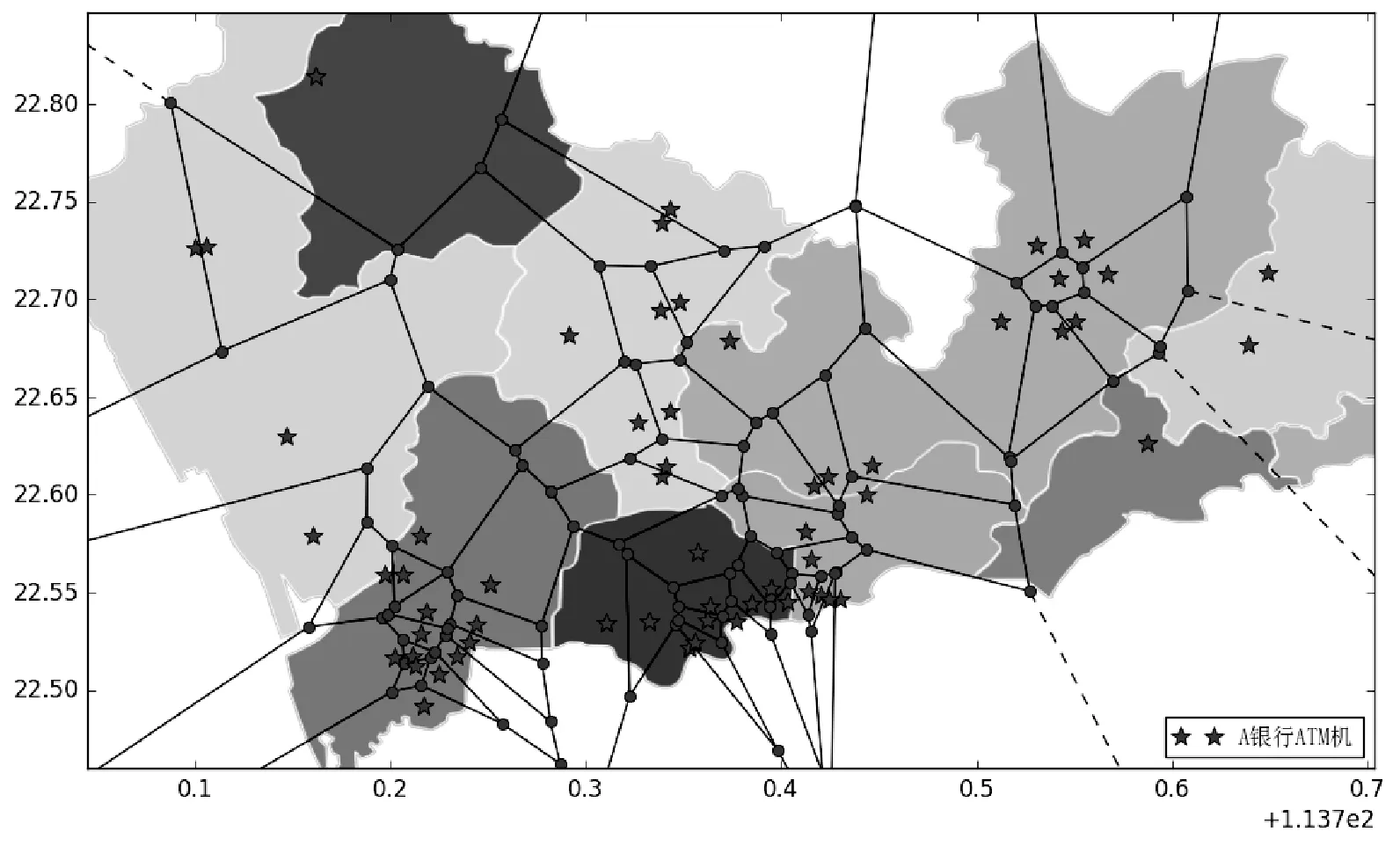
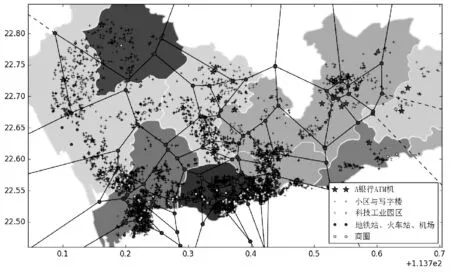
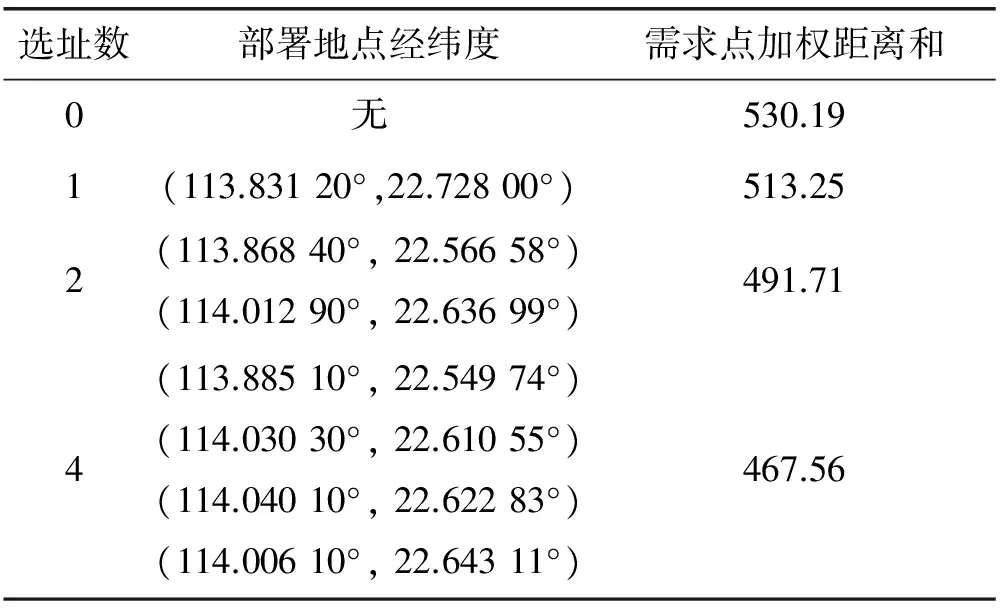
Si={x∈X|d(x,si) (1) 图1 Voronoi图示例 假定在空间中已有B银行的T个ATM部署点,添加P个ATM部署点,则空间中B银行共有T+P个ATM部署点s1,s2,…,st+p。以B银行ATM为生成元对空间建立Voronoi图,每个Voronoi图区域内有M个需求点c1,c2,…,cm,对应的需求值分别为w1,w2,…,wm,N个竞争点竞争值分别为b1,b2,…,bn。ATM选址数学模型如公式所示: (2) 对每一个Voronoi区域,如果该区域的竞争值之和越大,即式(2)中的分母越大,那么该区域的用户将更有可能被竞争点分流,该区域的需求点的权重将更小,模型优化过程中将避免在此类区域添加ATM。 K中心点聚类是K均值聚类算法的一种变体。K中心点聚类考虑将N个数据点分为K个组,使得每个组内的数据点之间的距离较小,而不同组数据点之间的距离较大。与K均值聚类不同,K中心点聚类仅以数据点本身为簇中心,以减小对异常数据的敏感性。劳埃德算法[9]是一种常见的K中心点聚类算法,算法步骤如下: 输入:N个数据点和簇数目K 输出:K个簇 1. 从N个数据点中随机选择K个点作为初始簇中心点; 2. 计算每个数据点到K个簇中心点的距离,将数据点分配到距离其最近的簇中心点形成K个簇; 3. 在每个簇中,选取一个新的簇中心点使得簇中其他点到簇中心点的距离和最小; 4. 如果数据点到其所属簇中心的距离和的变化在预设精度内,则算法停止,否则回到步骤2。 在一般的图结构中,P-Median问题的计算复杂性是NP难题,但Hakimi[3]证明P-Median问题中总有一组最优解使得P个设施的部署位置位于空间中的需求点上,这个结论被称为Hakimi性质。基于Hakimi性质,本文使用一种修改的劳埃德算法将新添加的ATM部署点置于空间中的需求点上。经典的劳埃德算法在迭代过程中所有的簇中心均发生更新,本文提出的ATM选址模型系基于空间中已有的ATM,因此在算法迭代过程中将以B银行已有ATM为固定簇中心不进行更新。本文首先在B银行已有ATM所在位置添加一个需求值为无穷大的需求点以保证已有ATM为固定簇中心在迭代过程中保持不变,算法步骤如下: 输入:N个需求点与竞争点,K个已有B银行ATM部署点,新增ATM部署点数目P 输出:K+P个ATM部署点 1. 计算空间中每个需求点的需求值与每个竞争点的竞争值; 2. 在B银行已有K个ATM处添加需求值为无穷大的需求点; 3. 在空间中随机选择P个点为新ATM部署点; 4. 基于B银行所有K+P个ATM部署点对空间建立Voronoi图; 5. 计算每个Voronoi图区域内的竞争值; 6. 在每个Voronoi图区域内选取需求点为新部署点使得区域中其他需求点到新部署点竞争值衰减的加权距离和最小; 7. 如果所有部署点的位置变化在预设经度内,算法停止,否则回到步骤4。 本文以深圳市B银行(某真实的商业银行)为例,应用ATM选址模型选取新的ATM部署地点。B银行市场中已有的ATM部署地点有59个,以B银行已有ATM部署点对深圳市建立Voronoi图的结果见图2,深圳市ATM需求点分布见图3,B银行ATM的竞争点分布见图4。 图2 B银行已有ATM建立Voronoi图 图3 深圳市ATM需求点分布 选址数部署地点经纬度需求点加权距离和0无530.191(113.83120°,22.72800°)513.252(113.86840°,22.56658°)(114.01290°,22.63699°)491.714(113.88510°,22.54974°)(114.03030°,22.61055°)(114.04010°,22.62283°)(114.00610°,22.64311°)467.56 应用ATM选址模型为B银行分别添加1、2、4个新ATM部署地点,结果见表2。计算和实验结果表明仅添加4个B银行ATM部署点就可将所有需求点的加权距离和减小11.8%。 本文通过筛选与ATM选址相关的需求点,考虑多银行ATM的竞争影响并基于市场中已有ATM,构建一种更符合真实市场情况的ATM选址模型,并设计了一种基于Voronoi图和K中心点聚类的模型求解算法。由于影响ATM选址的因素诸多且复杂,在模型设计过程中,描述了考虑加入哪些因素和如何确定各个因素的权重等棘手问题的解决方法。在模型中加入更多的因素通常可以使模型更接近真实情况,但同时也会增加模型的复杂度,使得模型求解难度增加。如何根据不同的应用场景和求解目的,平衡模型的复杂度与求解难度,是一个具有应用价值的研究方向。 [1] Hakimi S L.Optimum Distribution of Switching Centers in a Communication Network and Some Related Graph Theoretic Problems[J].Operations Research,1965,13(3):462-475. [2] Hakimi S L.Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph[J].INFORMS,1964,12(3):450-459. [3] Kariv O,Hakimi S L.An Algorithmic Approach to Network Location Problems.II:The p-Medians[J].Siam Journal on Applied Mathematics,1979,37(3):539-560. [4] Nenad Mladenovic,Brimbergb J,Hansenc P,et al.The p-median problem:A survey of metaheuristic approaches[J].European Journal of Operational Research,2007,179(3):927-939. [5] Zineldin M.Bank strategic positioning and some determinants of bank selection[J].International Journal of Bank Marketing,1996,14(6):12-22. [6] 黎雯,周廷刚,张伟.GIS空间分析与模糊综合评判在银行ATM网点选址中的应用[J].测绘科学,2008,33(1):229-231. [7] 戴晓爱,李丽.GIS与模糊综合评判方法在垃圾填埋场选址中的应用[J].测绘科学,2011,36(5):128-130. [8] 陈军.Voronoi动态空间数据模型[M].北京:测绘出版社,2002. [9] Lloyd S P.Least squares quantization in PCM[J].IEEE Transactions on Information Theory,1982,28(2):129-137.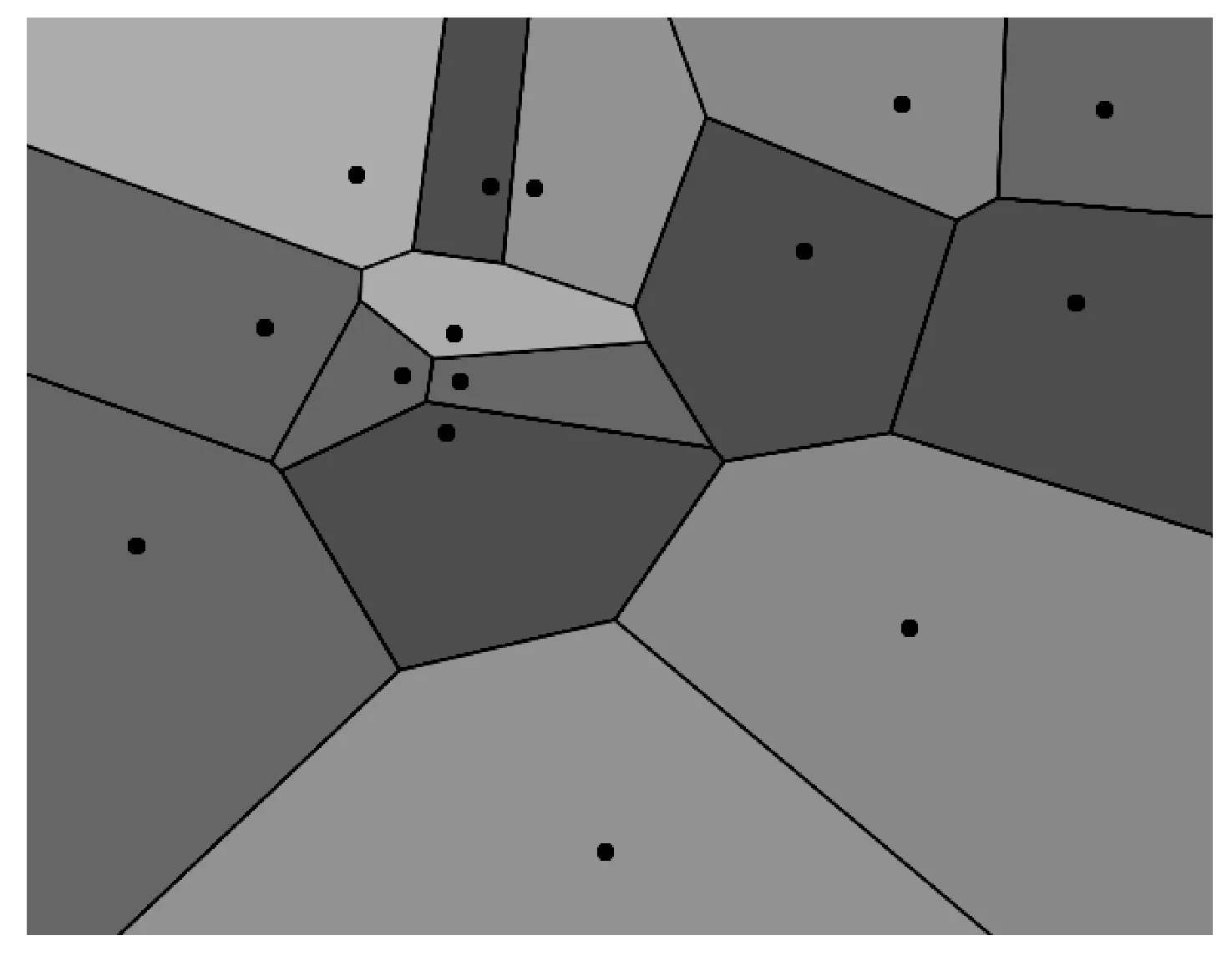
2.3 ATM选址数学模型
3 算 法
3.1 K中心点聚类与劳埃德算法
3.2 K中心点聚类与ATM选址
4 实验结果
5 结 语

