求解TSP问题的自适应模拟退火蚁群算法

袁汪凰　游晓明*　刘　升　朱　艳

1(上海工程技术大学电子电气学院　上海 201620) 2(上海工程技术大学管理学院　上海 201620)

0　引　言

旅行商问题TSP(Traveling Salesman Problem)是一个属于NP-Hard的组合优化问题。旅行商从所有城市列表中任选一个城市作为起点，不重复地遍历完所有城市，最后回到原起始点，从而形成一个最短路径的Hamilton回路。目前解决TSP问题的算法有最近邻点[1]、贪心算法[2]、遗传算法[3]、模拟退火算法[2]、粒子群优化算法[4]、蚁群算法[5]等。而蚁群算法是一个全局搜索策略的群智能算法，具有很好的自组织性、鲁棒性、正反馈性、并行性和易与其他算法结合解决实际问题等优点。但是蚁群算法同时也存在收敛速度慢、易陷入局部最优、容易陷入早熟、停滞的缺点。

蚁群算法最早由意大利学者M.Dorigo受到自然界中蚂蚁群体的觅食行为的启发首次提出，并将其应用于经典的TSP问题。其后专家学者对蚁群算法进行了改进：1996年M.Dorigo等在此基础上，提出了蚂蚁系统AS(Ant System)[5]，该算法采用随机比例规则构建路径，当所有蚂蚁路径构建结束之后，进行信息素更新；1997年M.Dorigo和M.Gambardella将蚁群算法中加入Q-Learning算法，提出了一种具有全新机制的蚁群系统ACS (Ant Colony System)[6];此后T.Stutzle等在AS基础上进行改进，提出了最大-最小蚁群算法MMAS (Max-Min Ant System)[7]。在这些改进算法中，MMAS是对AS完善的典型代表之一，在解决TSP问题上具有的良好性能。

MMAS在一定程度上有效地避免了算法的停滞，但仍存在解质量不高、收敛速度较慢等不足，因此专家学者在此基础上进行了改进。文献[8]提出一种动态的最大最小蚁群算法DMAS,通过构造与当前迭代过程中信息素最大值相关的函数，动态更新信息素的下限阈值，增大蚂蚁的探索能力，使得多样性增加；同时在DMAS中加入2-opt改善了解的质量。文献[9]在MMAS基础上运用混沌Tent映射全局遍历，寻找初始较优的候选路径，初始化信息素；当检测到算法陷入停滞时，采用混沌扰动，增加算法跳出局部最优的能力，具有较优的全局搜索能力。文献[10]提出一种NMMAS，该算法在两个阶段更新信息素，第一阶段为了使算法的探索能力增强，按顺序等级更新，第二阶段更新当前迭代最优路径，加快了收敛速度。文献[11]提出了基于MMAS的双种群最大最小蚁群算法，该算法采用双种群并行搜索机制，一定条件后在种群间进行信息素通信，直到信息素达到平衡，提高了解的质量。文献[12]根据K邻域候选集，前期采用局部搜索产生的解进行初始化信息素矩阵，再根据解的分布情况，动态地更新信息素，后期用3opt对解进行优化，并采用metropoil准则在一定概率内接受较优解，在较大规模的TSP问题上得到了较好的应用。上述文献虽然在一定程度上改善了解的质量但还存在收敛速度方面的问题。文献[13]提出了模拟退火蚁群算法，一次迭代后对所有蚂蚁求得的解采用更新策略，然后选取较优的几只蚂蚁更新信息素。同时引入Boltzmann机制，对每代蚂蚁生成的解进行处理，避免陷入局部最优，在解决Jop-Shop问题上有效地提高了算法的收敛速度。本文借鉴文献[13]在Jop-Shop问题上将模拟退火机制引入蚁群算法，提高了收敛速度的优势，提出自适应的模拟退火蚁群算法以用于解决TSP问题。

本文提出的自适应SA-MMAS算法，在MMAS算法中引入模拟退火机制，在高温阶段以一定概率接受其他解，增加蚁群的搜索空间；在低温阶段能够一定程度上提高收敛速度。并在全局信息素更新中引用了模拟退火衰减函数，采用一种自适应的信息素挥发机制进行信息素更新，使得算法前期的搜索能力增强寻到更多可行解，后期使得算法收敛速度加快，缩短找到最优解的时间。通过双重作用使得该算法能够更好地平衡种群多样性和收敛速度的矛盾，同时采用3opt局部搜索算法更进一步提高了解的质量。

1　相关工作

1.1　基本蚁群算法

蚂蚁虽然没有视觉的，但是却可以通过合作完成任务，蚁群中后续蚂蚁根据前期蚂蚁从蚁穴出发寻找食物再回到蚁穴过程中释放的一种化学物质—信息素，来寻找路径。前期蚂蚁在寻找路径时先会随机选择一个路径前行并释放出相应的信息素，若信息素浓度越高，即选择该条路径的蚂蚁数越多；若信息素浓度越低，此时选择该路径上的蚂蚁数目越少，通过这种正反馈作用，最后找出一条最优路径。为了避免局部最优，即采用一种挥发机制，使得路径上的信息素不是一味的叠加，通过这种负反馈作用，以便蚂蚁避免局部最优，找到全局最优路径。蚂蚁在寻找最优路径的同时，采用轮盘赌以一定概率选择其他路径。当该路径比当前最优路径短时，将会有更多蚂蚁走该条路径，就可找到最短路径。

假设蚂蚁的数量为m，城市的规模为n，将m只蚂蚁随机分配到n个城市中，τij(t)为t时刻蚂蚁k(1,2,…，m)残留在(i，j)之间的信息素浓度，初始时刻各城市间信息素浓度相同，即设置τij(0)=const。每只蚂蚁根据各个路径上的信息素浓度选择转移路径的方向，蚂蚁k从i城市转到j城市时采用状态转移概率：

(1)

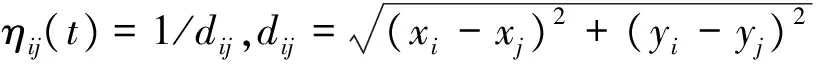
τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(2)

(3)

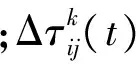
(4)

式中：Q为信息素强度；Lk为蚂蚁k在当前循环中所走路径的总长度。

1.2　MMAS算法

最大-最小蚁群算法(MMAS)通过将信息素限定在某一区间，避免了某一条路径上信息素的持续积累，在一定程度上有效地避免了算法的停滞，该算法在TSP、QAP[14]和VRP[15]等问题有较优的解。MMAS与基本蚁群算法相比其改进的几点优化之处为:

(1) 为了避免算法早熟、停滞，MMAS算法将各边的信息素限制在一定范围[τmin，τmax]，若τij≤τmin，τij=τmin；若τij≥τmax，τij=τmax其中τmax和τmin的计算公式[6,8]分别为式(5)、式(6)：

(5)

(6)

式中：Tgb是全局最优路径。

(2) 每迭代一次，有且仅有一只蚂蚁进行信息素更新，即对当前最优路径或者全局最优路径进行更新，使最优解得到有效的利用，算法的探索能力也会增强。信息素更新规则表示为：

(7)

(8)

式中：f(sbest)为当前最优或者全局最优的路径长度。

(3) 算法中每条边的信息素初始化为τmax。增加了算法初始阶段的随机搜索能力。

1.3　3-opt[16]

局部搜索算法对蚁群每次迭代过程中产生的解进行优化，而在局部优化算法中3-opt算法效率比较高，其基本流程为：随机选择搜索区域内的某些位置，随后从当前位置移动到相邻位置，将候选解转换成另外一个，该算法反复执行减少路径的长度，直到达到极优解。

设T为当前路径，在每一步迭代中，算法试图发现两个不相交的边集X={x1,x2,…,xk}和Y={y1,y2,…,yk}，其中X、Y初始化是空集，按步骤i添加一对边xi和yi。其中xi、yi和yi、xi+1必须分别共享端点，且令t1表示端点x1，在i≥1的情况下有xi=(t2i-1,t2i),yi=(t2i,t2i+1)和xi+1=(t2i+1,t2i+2) 。如图1所示。

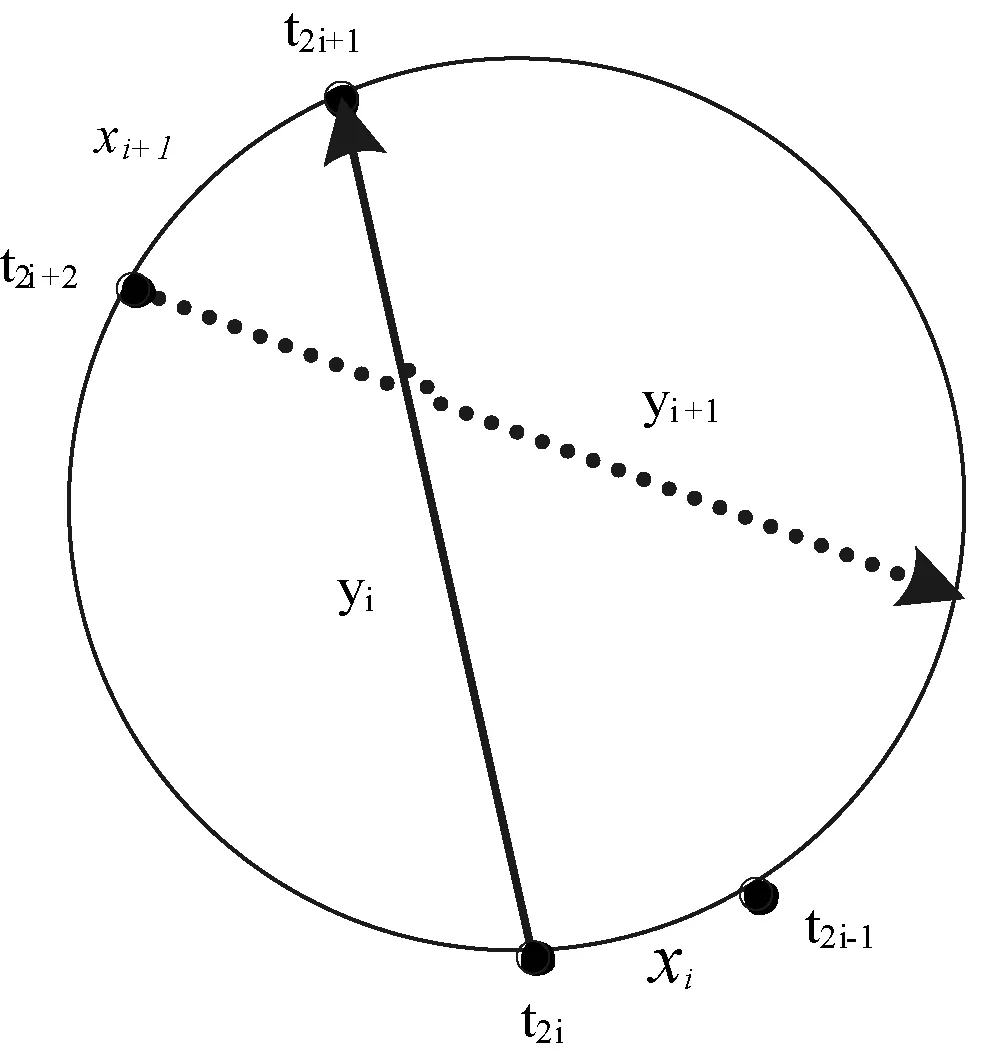
图1　xi，yi，xi+1,yi+1的制约性选择

X边集被从T中删除由Y替代能找到更好的路径仍构成一个封闭回路，如图2所示。

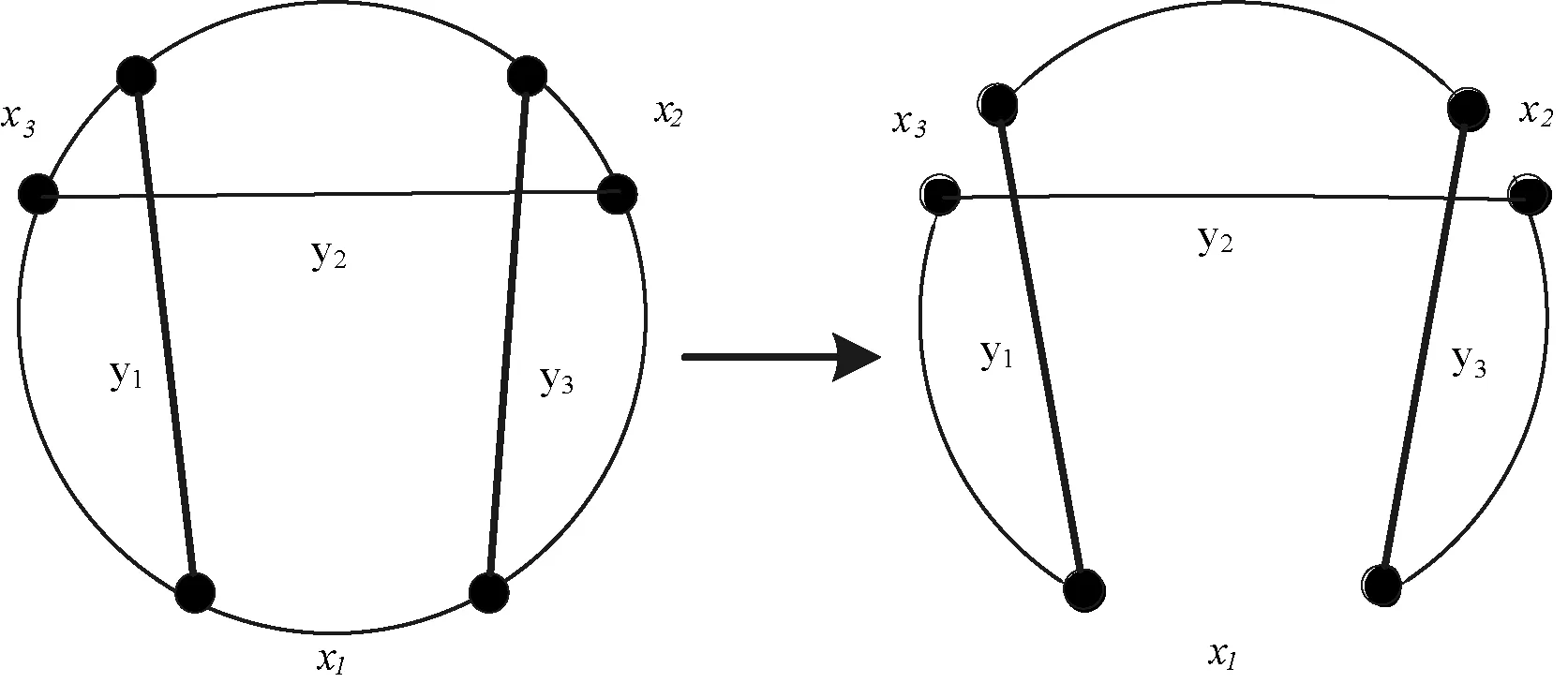
图2　3opt：x1,x2,x3被y1,y2,y3替换

2　改进算法

2.1　模拟退火机制的引入

模拟退火算法SA(Simulated Annealing)是一种模拟物理中固体退火过程而设计的全局搜索优化算法，最早在1953年由Metropolis等人提出。采用模拟固体退火的加温、等温和冷却三个阶段，具体如下：先在一个高温状态下(相当于算法随机搜索)，然后逐渐退火(Metropolis抽样过程)，在每个温度下(相当于算法的每一次状态转移)逐渐冷却(相当于算法局部搜索)，最终达到能量最低态(相当于算法找到最优解)。

设系统温度为T，初始温度T(0)=T0，当蚁群算法完成一次迭代后，可以得到初始解集S1，其中被3opt优化过的最优解路径长度为LRoute，在初始解集基础上随机扰动产生最新集S2，由新解集计算出的路径长度为L2，目标函数变化的差值为：

ΔL=L2-LRoute

(9)

当ΔL<0时，接受S2作为新的当前解，否则新解集的接受概率如下：

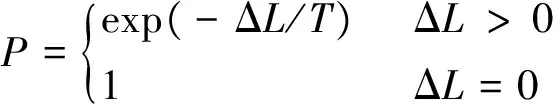
(10)

即产生(0,1)区间上均匀分布的随机数ζ，若P>ζ,则接受S2作为新的当前解；否则保留原解，最优解仍为LRoute。

完成一轮循环和信息素更新后进行降温，即T(NC+1)=a×T(NC),若降温系数a取值较小，温度下降越慢，算法的收敛速度会加快，但可能很容易陷入局部最优。所以本文加入了回火机制(类比于金属淬火处理的最后阶段回火)，即人为设置升温过程，适当概率接受高能状态，以一种随机扰动的方式，帮助算法跳出局部最优，再进入模拟退火的过程。回火温度范围为[Tmin,Tmax]，回火次数为Hs，回火最大次数为Hmax。当温度T降到Tmin时，算法使得T立即回升到Tmax，以较高的概率接受较差解加入最新集，大大地减少了落入局部最优的可能性。

2.2　改进的信息素更新算子

信息素挥发因子ρ的大小在某种水平上影响路径上的信息素量，同时其大小影响了算法的全局搜索能力和收敛速度。传统蚁群算法中，信息素挥发因子是属于(0,1)范围的一个固定常数。ρ值越大，路径上的信息素量残留越少，蚂蚁搜索路径的随机性变大，提高了算法的全局搜索能力，易找到全局最优解，但是却导致算法的收敛速度降低。ρ值越小，路径上信息素量的残留越多，蚂蚁选择之前走过的路径概率越大，加剧了算法的收敛速度，但容易陷入局部最优。对此，本文根据模拟退火算法中衰减函数对寻优结果的影响，提出了一种自适应的信息素更新方式。在搜索前期ρ取值较大，增加算法的全局搜索能力，使得蚂蚁能够遍历到所有路径；后期取值较小，加快算法的收敛速度，缩短搜索时间。可见是与迭代次数NC有关的，因此信息素挥发因子ρ改进为:

ρ(NC)=1/log2(1+NC)

(11)

2.3　算法描述

算法步骤如下：

Step1： 参数初始化；

Step2：NC=0，随机分配m只蚂蚁起点;

Step3： 蚂蚁k根据式(1)和轮盘赌方式选择下一可行城市;

Step4： 所有蚂蚁都完成搜索任务，蚁群得到初始集S1，初始集中最优个体LRoute;

Step5： 采用3-opt对当前初始解中最优个体LRoute进行局部优化;

Step6： 根据模拟退火原理产生新的可行解S2,按照式(9)判断是否接受新解作为当前解，生成最新集；

Step7： 根据式(7)计算自适应挥发素；

Step8： 根据式(5)、式(6)计算最大最小信息素值；

Step9： 根据最新集里的解以及当前最优个体，按照式(4)、式(7)、式(8)对信息素进行更新；

Step10： T←aT,NC←NC+1;

若T≥Tmin,则转Step3;

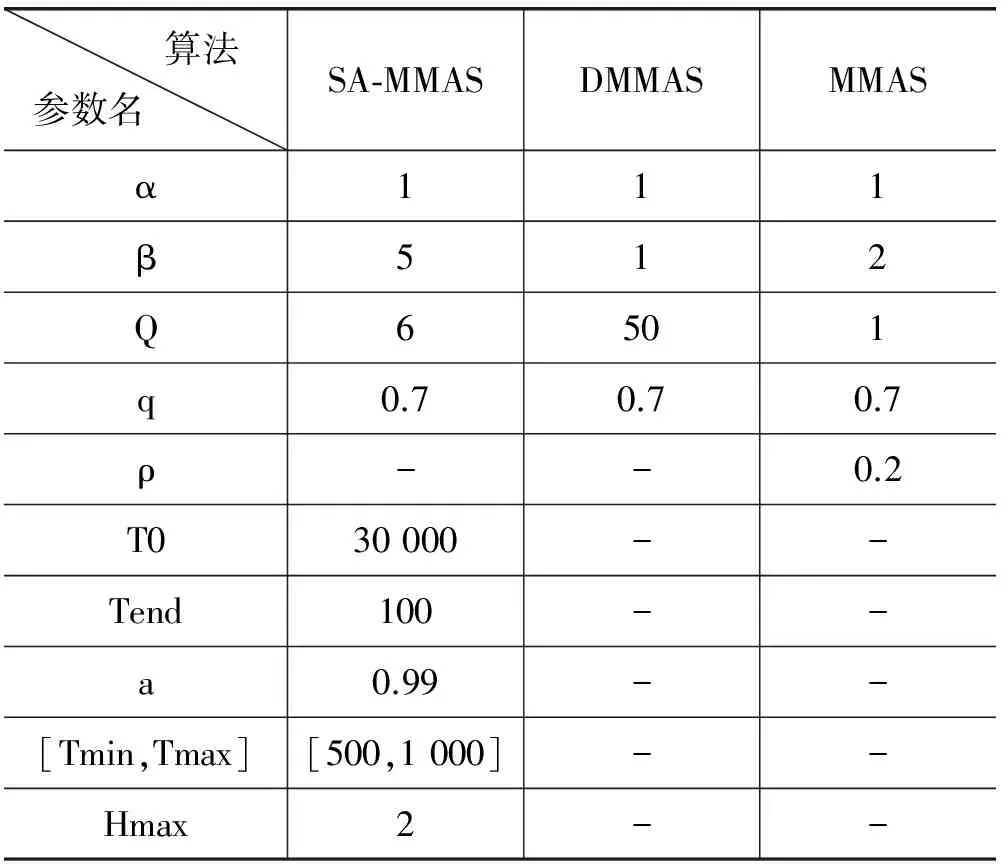
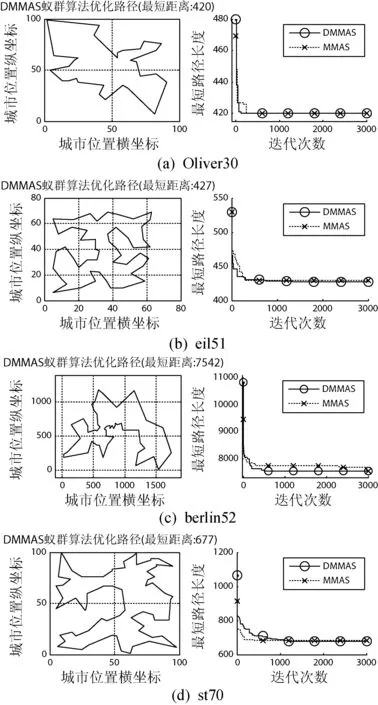
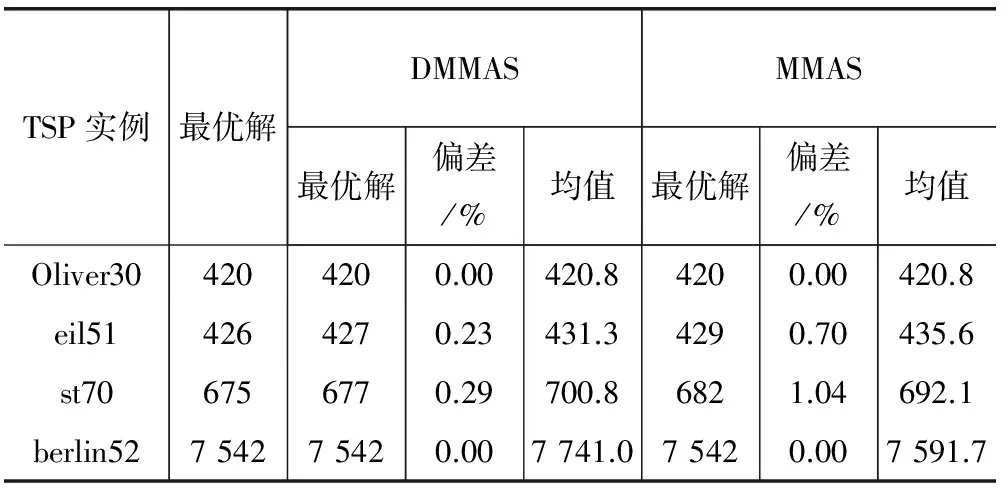
若T

若T

Step11： 输出最优解。

其中，Step6引入模拟退火机制，以一定概率接受随机扰动产生的新解，增强了算法的全局搜索能力；Step9通过自适应的信息素更新机制，前期使蚂蚁找到更多可行解，后期加快了收敛速度；Step10通过回火策略，减少了算法陷入局部最优的可能性。

3　实验仿真与结果分析

为了检验本文算法的性能，使用MATLAB 2014a对TSPLIB测试集中的部分城市进行仿真，分别对DMMAS(MMAS中加入自适应信息素算子)与MMAS，SA-MMAS与MMAS进行比较，验证了算法的优越性。参数设置如表1所示，其中MMAS参数设置参考文献[8]的建议值,算法的蚂蚁数目m等于城市数n。

表1　参数设置

本文以Oliver30、eil51、berlin52、st70为对象分别对DMMAS与MMAS进行了10次实验，每次迭代3 000次。将DMMAS与MMAS进行对比，DMMAS的优化路径图以及DMMAS与MMAS最短路径对比图如图3所示。在图3的4个例子可以看出：DMMAS算法的收敛精度以及收敛速度优于MMAS算法。从表2中也可以看出DMMAS算法的最优解更接近于最优解。

图3　MMAS与MMAS对比

TSP实例最优解DMMASMMAS最优解偏差/%均值最优解偏差/%均值Oliver304204200．00420．84200．00420．8eil514264270．23431．34290．70435．6st706756770．29700．86821．04692．1berlin52754275420．007741．075420．007591．7

为了将本文算法SA-MMAS与MMAS进行比较，本文选取了6种不同规模的TSP测试集进行实验。从表3中可以看出，本文算法无论是从最优解、均值还是迭代次数对于TSP问题的求解皆优于MMAS算法。

表3　SA-MMAS算法与MMAS算法比较结果

以KROA100为例，图4为求解KROA100的最优路径图和迭代图，本文算法求得KROA100最优解为21 282，与TSP最优解误差为0%，比MMAS小了0.37%；本文在迭代第188次时收敛，比MMAS少了1 573；平均迭代次数469，比MMAS少了1 338，可以看出收敛速度以及求解精度明显优于MMAS算法。

图4　KROA100

4　结　语

本文针对TSP问题提出了自适应模拟退火蚁群算法。通过对不同规模的城市进行仿真，结果表明，在蚁群算法中加入自适应信息素更新算子，前期增加了算法的全局搜索能力，后期加快了算法的收敛速度。而在蚁群算法中引入模拟退火机制，高温阶段提高了算法的全局搜索能力，低温阶段加快了算法的收敛速度且有效地避免陷入局部最优。在不同规模的TSP问题上，本文算法结合以上两种机制，经多次实验表明不仅可以提高解的质量，而且可以较好地提升算法的收敛速度，从而使整个算法的运行效率更加优化。因此，本文算法比传统的MMAS算法性能更优，在今后的工作中会进一步研究自适应信息素模型，使算法具有更好的性能。

[1] 饶卫振,金淳,黄英艺,等.求解TSP问题的最近邻域与插入混合算法[J].系统工程理论与实践,2011,31(8):1419-1428.

[2] 李金旭,黄悦悦.求解TSP的贪心模拟退火算法[J].河南工程学院学报(自然科学版),2015(1):66-69.

[3] 于莹莹,陈燕,李桃迎,等.改进的遗传算法求解旅行商问题[J].控制与决策,2014(8):1483-1488.

[4] 李文,伍铁斌,赵全友,等.改进的混沌粒子群算法在TSP中的应用[J].计算机应用研究,2015,32(7):2065-2067.

[5] Dorigo M,Maniezzo V,Colorni A.Ant system: optimization by a colony of cooperating agents[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society,1996,26(1):29.

[6] Dorigo M,Gambardella L M.Ant colony system:a cooperative learning approach to the traveling salesman problem[J].IEEE Transactions on Evolutionary Computation,1997,1(1):53-66.

[7] Stutzle T,Hoos H H.MAX-MIN Ant system[J].Future Generation Computer Systems,2000,16(9):889-914.

[8] Bonyadi M R,Shah-Hosseini H.A dynamic max-min ant system for solving the travelling salesman problem[J].International Journal of Bio-Inspired Computation,2010,2(6):422-433.

[9] 耿志强,邱大洪,韩永明.基于混沌的MMAS算法及其在旅行商问题中的应用[J].计算机工程,2016,42(3):192-197.

[10] Zhang Z J,Feng Z R.A novel Max-Min ant system algorithm for traveling salesman problem[C]//IEEE International Conference on Intelligent Computing and Intelligent Systems.IEEE,2009:508-511.

[11] Zhou X,Zhao L,Xia Z,et al.A Max-Min Ant System with two colonies and its application to Traveling Salesman Problem[C]//2012 IEEE Fifth International Conference on Advanced Computational Intelligence (ICACI),2012:319-323.

[12] 陈星宇,全惠云,肖伟.求解旅行商问题的高效自适应混合蚂蚁算法[J].计算机工程与应用,2007,43(27):84-87.

[13] 张晓婧,高慧敏.基于模拟退火的蚁群算法求解Job-Shop问题[J].计算机应用与软件,2008,25(5):77-79.

[14] 牟廉明,戴锡笠,李坤,等.求解二次指派问题的最优迭代最大最小蚂蚁算法[J].计算机应用,2014,34(1):199-203.

[15] 谢骊玲,宋彦斌,杨坦,等.求解车辆路径问题的改进MMAS算法[J].计算机技术与发展,2016,26(3):27-30,35.

[16] Helsgaun K.General k-opt submoves for the Lin-Kernighan TSP heuristic[J].Mathmatical Programming Computation,2009,1(2/3):119-163.