用于分类决策的有序判别指标性能比较

裴生雷　贾国庆　叶利娟

1(青海民族大学物理与电子信息工程学院　青海 西宁 810007) 2(青海民族大学数学与统计学院　青海 西宁 810007)

0　引　言

在传统的分类任务中，人们很少去考虑数据的有序性。然而现实世界中很多任务都存在这类问题，特征值的序关系，可以更好地描述数据本身的特点，使用户获得潜在的偏好信息。在解决多属性决策问题时，有序特征的评价指标就显得非常重要。这些指标可以用于有限决策方案的排序择优问题，可以应用于信用评价、顾客满意度评估、社会调查统计、故障诊断等领域[1-5]。在这里我们举一个例子，来说明数据本身具备的有序特征。假设信用评价任务中存在三个条件属性(历史信誉、收入和学历)用于描述客户，决策属性是信用等级。在这里，如果客户X的三个条件属性值比客户Y的好，那么X的信用等级也不比Y的差。这类问题中，对象的条件属性和决策属性存在序关系，即属性值之间是可以比较大小。目前，在机器学习、数据挖掘和智能决策领域中越来越引起研究人员的重视。

有序分类问题中，随着研究的深入和发展，特征评价指标也得到了改进和发展。有序条件熵、排序互信息、排序基尼不纯度可以很好地判断排序一致性，进而获取有效的特征，完成数据的分类或者决策模型的优化[6-7]。但是，模型由于应用不同有序判别指标，导致分类任务的效果有所不同。这三个指标，在决策树模型中应用较多，例如经典C4.5算法使用的评价指标是信息增益，即互信息；CART决策树使用的评价指标是基尼不纯度。在实际应用中应考虑有序特征评价指标的选择问题，文中主要针对这三个有序特征判别指标进行分析，以方便用户更好的根据实际需求选择必要的指标，完成特征评价。

1　有序特征评价指标

本文引入三个有序分类的特征评价指标。它们是目前应用比较广泛的特征评价指标，较好地反映两个变量之间的排序一致性，即反映出变量值之间序的关系，特征值好的样本应该被分到好的类别中。

假设给定有序数据集U={x1,x2,…,xn}，特征集A={a1,a2,…,am},B⊆A，Y是一组类标记，并且有yi是xi的类标记。

1.1　有序条件熵

有序条件熵是胡清华教授等于2010年提出的用于有序分类的判别指标，能够反映特征值之间的序关系，用于评价特征质量[6]。在香农熵基础上定义的有序条件熵，考虑了对象之间的序结构，可以有效地度量特征和决策之间的排序一致性。由于继承了香农熵的鲁棒性特点，使得单个噪声样本不会引起概率分布的变化。香农熵是数据不确定性的度量，不确定程度越高，熵值越大。

有序条件熵是基于概率分布函数计算的，由于属性值之间存在序关系，因此被分为向上的有序条件熵和向下的有序条件熵。给定属性集C，且C⊆A，如果C已知的情况，B的不确定性信息表示为关于C的向上的有序条件熵或者是向下的有序条件熵，形式化定义如下[6]。

向上的有序条件熵：

向下的有序条件熵：

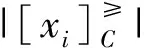
1.2　排序互信息

排序互信息的提出有效地改进了有序条件熵，能够有效地刻画变量之间单调一致性程度，因此可以应用于多标准决策属性的相关性和依赖性分析，以及有序分类学习。排序互信息受互信息的启发而提出，依据排序条件熵和排序熵的形式化定义推导产生。它反映了对象根据属性值提供的信息进行排序的一致性程度，而不是分类的一致性程度。

假设给定有序数据集U={x1,x2,…,xn}，包含属性集A，其中B⊆A，C⊆A，数据集U关于B和C的排序互信息，形式化定义如下[6]。

向上的排序互信息：

向下的排序互信息：

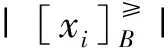
1.3　排序基尼不纯度

基尼不纯度与熵都是数据不确定性的度量，两者的主要区别是熵达到顶峰的过程要慢一些，熵对于混乱数据集合的判罚要更重一些。基尼不纯度将来自集合的某种结果随机应用于某一数据项的预期误差率，基尼不纯度越小，纯度越高，集合的有序程度越高，分类效果越好，它主要应用于CART分类回归树。2015年，Masala受到排序互信息的启发，基于基尼不纯度提出了排序基尼不纯度作为单调分类的判定指标[7]。

排序基尼不纯度使用优势集替代了传统基尼不纯度的等价类，形式化定义如下：给定有序数据集U={x1,x2,…,xn}，包含属性集A，其中B⊆A，C⊆A，数据集U关于B的排序基尼不纯度定义如下[7]。

向上的排序基尼不纯度：

向下的排序基尼不纯度：

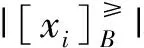
如果C已知的情况下，关于B的向下排序基尼不纯度形式化定义如下。

向上的有序条件基尼不纯度：

向下的有序条件基尼不纯度：

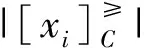
2　特征评价指标的判别能力

为了对各项排序判别指标有一个清晰的认识，为不同排序判别指标灵活运用于不同业务领域提供借鉴，需要对排序指标的判别能力做出分析和比较。下面通过算法1来判断不同指标是否能够很好地去选择属性，并进一步地发现单调函数以判别属性与决策的单调性，挖掘潜在的偏好信息。算法1是基于C4.5提出的，通过获得最好的特征来完成数据划分，递归的生成决策树，进而产生可理解的决策规则。

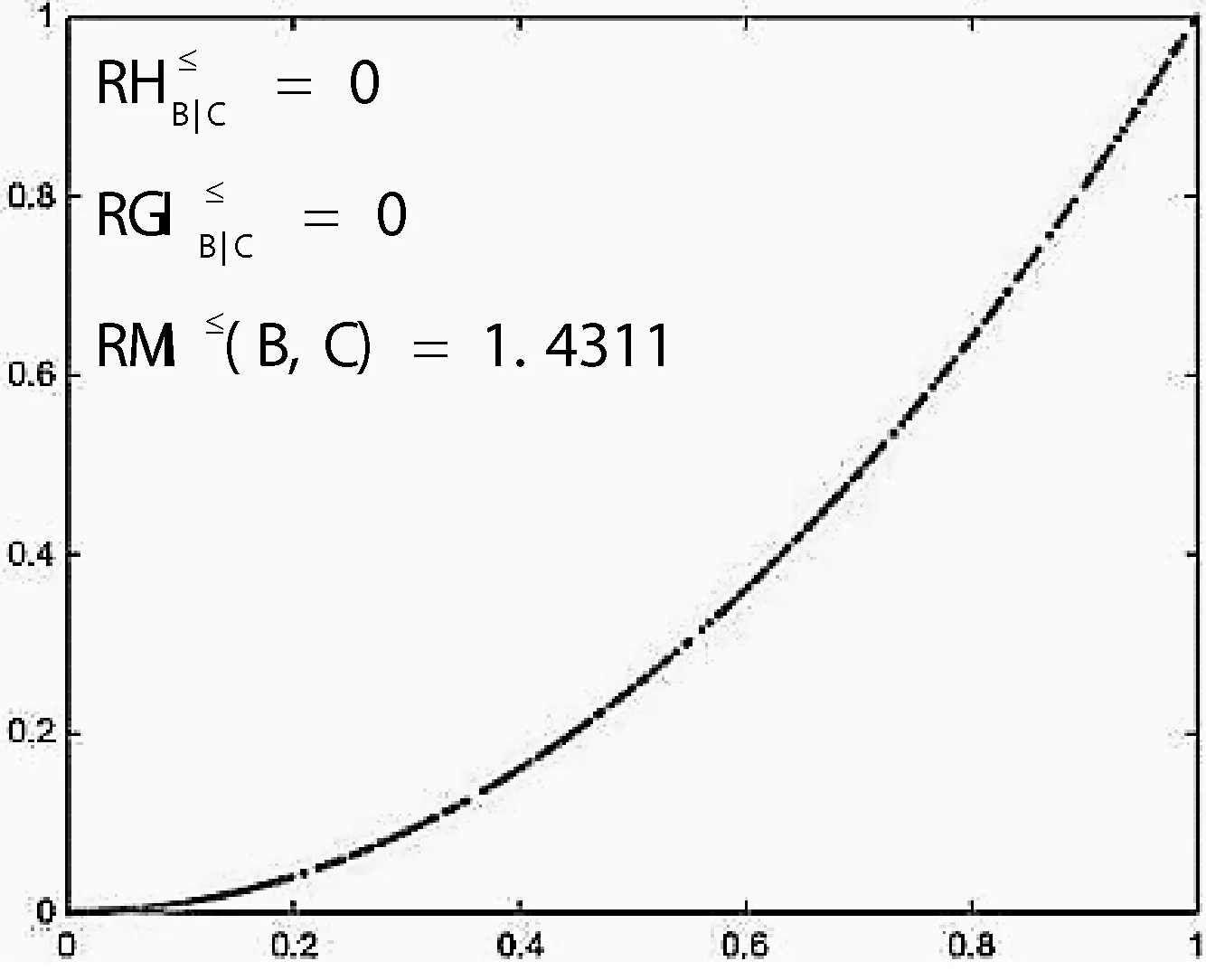
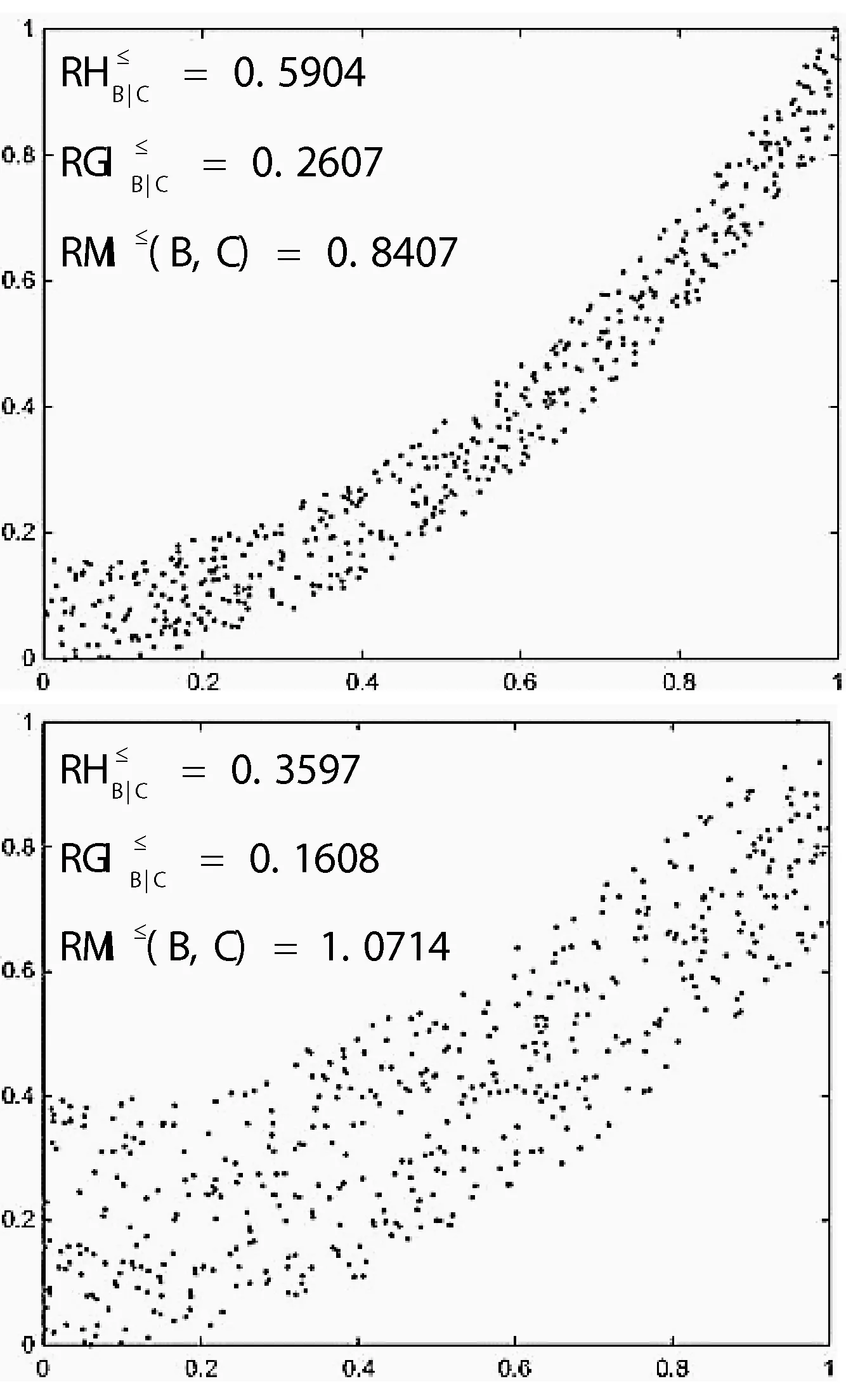
图1　不同指标的排序判别能力

通过观察图1，可以清楚的看到判别指标在三组不同数据上的变化情况，随着非单调噪声的增大各项判别指标都在发生变化。排序互信息的值在下降，并且下降较快，有较强的判别能力；其次是排序条件熵的值在上升，并且上升较快，具有一定的判别能力；最后是排序基尼不纯度的值也在随着噪声的增大而缓慢上升，表明其判别能力较好。

因此，这三项指标都能够有效地实现有序分类任务特征判别，然而排序条件熵和排序互信息对信息的混乱程度惩罚更重一些。在实际应用中要根据数据的不同特点选择合适的判别指标，以获得更好的分类效果。

3　实验分析

3.1　有序分类算法

通过设计的决策树算法对三种指标的评价效果做出分析，在真实的分类任务上进行性能比较[8-9]。根据有序分类问题的特点，使用了平均绝对误差对性能做出评价，可以看出基于排序互信息的决策树算法在三种指标中效果最好，排序条件熵和排序基尼不纯度效果非常接近。因此，在实际应用中，对于改进的C4.5和CART决策树中分别应用排序互信息和排序基尼不纯度将使得排序的一致性增强[10]。

有序决策树算法1：

输入：训练样本集合，样本用(A,D)来表述。停止参数：ε，L

输出：有序决策树。

// 根据不同判别指标的定义，对于排序互信息和序条件熵计算最大值，排序基尼不纯度计算最小值。

开始：

步骤1：生成决策树根节点；

步骤2：如果剩余的样本数小于L或者所有的样本属于同一类，则标记为叶节点，返回；否则，执行步骤3；

步骤3：对于每个属性Ai对于每个分裂点Ai=a计算排序判别指标的值，并得到每次的最大值(或最小值)对应的分裂点以及最大值(或最小值)；

步骤4：选择所有分裂点对应的排序互信息的最大值或最小值)；

步骤5：如果最大值(或最小值)小于ε，则标记叶节点，返回；否则继续执行步骤6；

步骤6：分裂点Aj=a划分父节点为左右子节点；

步骤7：依据左右子节点，递归的构造有序决策树。

输出：生成的有序决策树

当然，在实际分类任务中并不是所有的特征都是有序的，还存在部分有序的情况。对于这类问题，需要提出有效的有序分类特征选择算法，从而选择最好的特征完成数据划分，这是一种较为合理的思路。文献[4]中讨论的齿轮裂纹的严重性识别任务，提到混合特征存在时的解决方案，通过设计特征选择算法获取分类能力较强的故障特征子集，进而利用改进的遗传算法完成数据分类获得了较好的效果。针对这类任务的算法设计，可以参照文献[4]中的思路。

3.2　有序判别指标的鲁棒性分析

根据文献[11]中提到的算法生成单调数据集，并设计实验来分析在不同的单调程度下判别指标的排序性能，主要使用平均绝对误差(MAE)来评价,这是有序分类任务中的重要性能评价指标。生成训练样本600个，测试样本120个，属性5个，属性取值个数为5，样本共分为4类，其中测试样本非单调性指标(NMI)为0.2%。为了验证不同指标的鲁棒性，设置非单调性从0.2%逐步变化为1.2%，步长0.2%。

根据图2中的曲线走势可以看出，不同指标的性能随着单调程度的增大而发生变化。从趋势可以看出三种判别指标变化较为平缓，性能较为稳定，鲁棒性较强。其中，有序条件熵与排序互信息的随着非单调性的变化趋势较为一致，主要是因为都是以香农提出的信息熵为基础的。排序基尼不纯度变化也较为平缓，性能下降稍微明显一些。

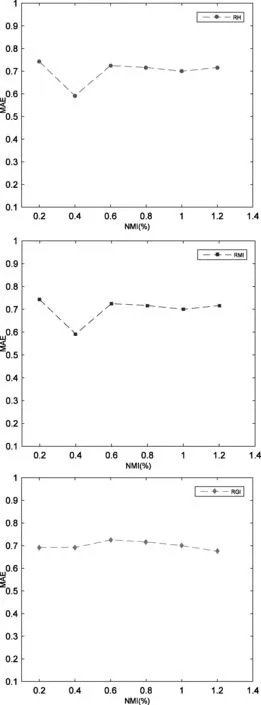
图2　判别指标的鲁棒性分析

3.3　有序判别指标在真实任务上的性能评价

本文利用算法1在UCI数据集上实验并分析对比[12]。使用三个向下的排序判别指标分别训练，并且基于十折交叉验证技术计算平均绝对误差(MAE)及标准差。

在表1中描述了三个向下的排序判别指标在10个任务上的性能比较，其中每个数据集对应的第一行表示十折交叉验证的平均绝对误差(MAE)，第二行表示十折交叉验证的标准差。表1中的最后一行表示在10个分类任务上MAE的平均值。

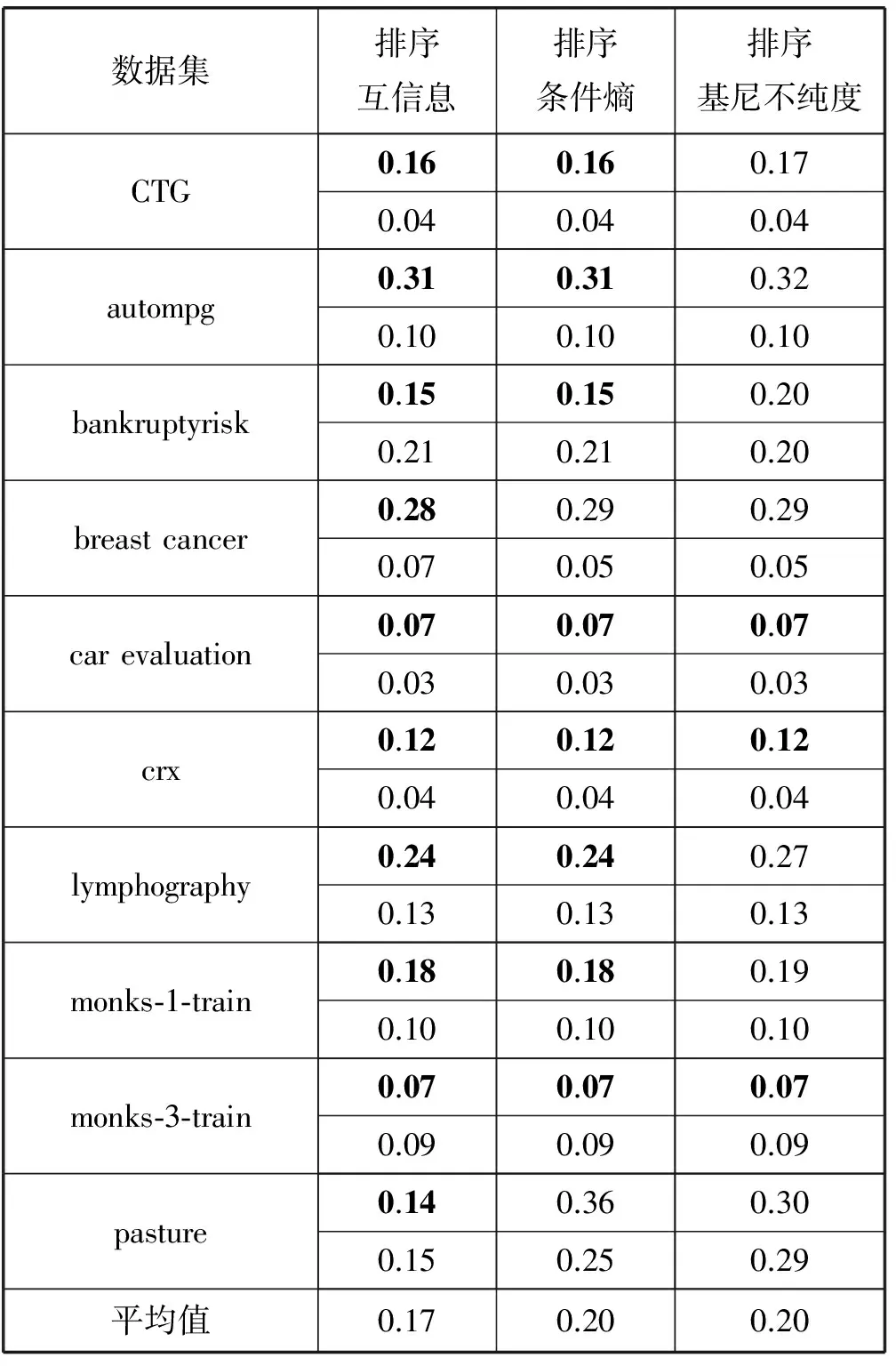
表1　排序判别指标在10个任务上的性能比较

通过表1中显示的平均绝对误差可以看出，排序互信息与排序条件熵在多数数据集上相同。然而对于10个数据集来说，排序条件熵与排序基尼不纯度的平均值相同。排序互信息在10个数据集上的平均性能高出3个百分点。根据统计检验确定不同判别指标的平均性能是否存在显著性差异，本文应用t检验两两比较了所有指标的平均性能，进而明确了排序互信息指标存在的优势[15-16]。

根据以上的实验分析，可以清楚的看到三种有序分类判别指标的效果，排序互信息具有很强的鲁棒性，性能较好。排序基尼不纯度在传统的基尼不纯度上提出，也大大增强了实际的有序分类效果，鲁棒性较强。在现实生活中的有序分类任务有很多，可以根据三种有序判别指标的特点进行选择，已达到预期效果和目标。

4　结　语

根据有序分类任务的特点，对三类有序判别指标的判别能力做出分析，给出不同任务下的平均绝对误差，以此判断三者的判别能力以及分类效果。对于包含噪声的样本，分别计算了三种有序判别指标，结果显示有序特征判别能力较强。然而，有序条件熵和有序排序互信息对混乱数据的惩罚更弱一些，并且性能更为接近。对三种指标的鲁棒性分析，显示三种判别指标度都较为鲁棒，排序互信息继承了互信息的鲁棒性特点，排序基尼不纯度继承了基尼不纯度的特点。通过判别指标的比较及其在决策树中的应用，可辅助不同领域人员构建适合需求的高效的有序分类模型，为从事相关研究工作的人员提供一定的参考。

[1] Greco S,Matarazzo B,Slowinski R.Customer satisfaction analysis based on rough set approach[J].Journal of Business Economics,2007,77(3):325-339.

[2] Tsumoto S.Mining Hierarchical Decision Rules from Clinical Databases Using Rough Sets and Medical Diagnostic Model[J].Information Sciences An International Journal,2004,162(2):65-80.

[3] Wang G,Ma J,Huang L,et al.Two credit scoring models based on dual strategy ensemble trees[J].Knowledge-Based Systems,2012,26:61-68.

[4] 潘巍巍,宋彦萍,于达仁.齿轮裂纹程度识别的有序分类算法[J].哈尔滨工业大学学报,2016(7):156-162.

[5] 李战江,句芳,修长柏,等.银行信用风险小样本评级模型的构建[J].统计与决策,2016(9):39-43.

[6] Hu Q H,Guo M Z,Yu D R,et al.Information entropy for ordinal classification[J].Science China Information Sciences,2010,53(6):1188-1200.

[7] Marsala C,Petturiti D.Rank discrimination measures for enforcing monotonicity in decision tree induction[J].Information Sciences An International Journal,2015,291(C):143-171.

[8] 潘伟,佘堃.基于偏好不一致熵的有序决策[J].计算机应用,2017,37(3):796-800.

[9] 王鑫,王熙照,陈建凯,等.有序决策树的比较研究[J].计算机科学与探索,2013(11):1018-1025.

[10] Hu Q,Che X,Zhang L,et al.Rank Entropy Based Decision Trees for Monotonic Classification[J].IEEE Transactions on Knowledge & Data Engineering,2011,24(99):1-1.

[11] Milstein I,David A B,Potharst R.Generating noisy monotone ordinal datasets[J].Artificial Intelligence Research,2013,3(1).

[12] Bache K,Lichman M.UCI Machine Learning Repository[J].University of California Irvine School of Information,2013,2008(14/8).

[13] 陈建凯,王熙照,高相辉.改进的基于排序熵的有序决策树算法[J].模式识别与人工智能,2014(2):134-140.

[14] 郑津杨,徐坤,李建强.用于RFID系统数据处理的排序邻居算法性能分析[J].计算机应用与软件,2016,33(12):207-210.

[15] 董跃华,刘力.基于均衡系数的决策树优化算法[J].计算机应用与软件,2016,33(7):266-272.

[16] 石建国.有序决策树在大学生综合素质测评中的应用研究[D].河北大学,2015.