一种用于表情识别的局部二维主成分分析算法

张日东　贾克斌

(北京工业大学未来网络科技高精尖创新中心　北京 100124)(先进信息网络北京实验室　北京 100124)(北京工业大学电子信息与通信工程学院　北京 100124)

0　引　言

人脸表情是个人情感信息体现的重要方式，是人们日常生活中交流的重要手段，经过心理学家A.Mehrabian的研究表明，在人与人的日常交往过程中，语言代表的信息仅占信息总量的7%，而表情包含的信息占信息总量的55%。所以采用计算机技术对人脸表情进行识别一直都是人们研究的热点。人脸表情识别过程包含表情图像预处理，对人脸进行检测，对检测出的人脸进行表情特征提取和对表情特征进行分类识别 4 部分。其中，最重要的环节就是表情特征提取过程，只有精准对表情特征进行提取，才能有效对表情进行分类和识别。20世纪70年代美国心理学家Ekman将表情分成6种基本类型[1]：高兴、伤心、生气、吃惊、厌恶、恐惧。本文也按照该分类标准，实现对这6种表情的特征提取。

近年来，研究者们有针对性地从两个方面展开对表情识别的研究：一方面是在经典算法的基础上进行改进；另一方面以深度学习算法为基础，构造新的特征提取算法。在采用深度学习的研究方面，文献[2]和文献[3]采用卷积神经网络算法提取人脸表情特征。前者在对表情图像进行基线卷积神经网络处理之前先对图像进行了一系列预处理过程，后者是先对表情图像归一化处理,接着再采用可训练的卷积核提取表情隐式特征，最后用最大池化方法降维处理隐式特征。结果表明以上算法提高了人脸表情识别的性能和泛化能力。但这类方法实现起来比较复杂，训练时间比较长，需要大量数据用来调参。在经典算法方面，文献[4]对经典算法局部二值模式LBP进行改进，提出一种基于不同方向的LBP算法。通过将当前像素和水平、垂直、对角3个方向的邻域像素进行灰度值比较，对当前像素进行重新编码，有效降低了噪声干扰。实验证明改进的算法比LBP算法有更强的鲁棒性。文献[5]用Gabor特征提取、LBP和LPQ算法相结合的办法对表情特征进行提取，该算法先利用Gabor小波对人脸表情图像进行处理，接着对处理完的图像再进行LBP和LPQ特征分析。经测试该算法虽然有较高的识别率，但提取的特征过程较复杂，难以做到实时性。文献[6]将经典算法主成分分析PCA算法与线性判别LDA算法进行结合。文献[7]采用经典算法主动外观模AAM定位特征点，接着通过尺度不变特征变换SIFT算法对特征进行描述。这两种算法都是将两组经过不同表达的特征向量进行融合，构成复特征向量，进而进行特征提取。经对比实验，相对于原始算法，改进后的算法在识别率上有了一定的提高。

纵观以上文献，表情特征提取算法的好坏应从以下几方面考虑：

(1) 能完整地保留人脸表情的最本质特征。

(2) 有较强抗干扰能力。

(3) 能有效降低提取的数据维度，减小存储量。

深度学习具有较高的准确率，但是其模型建立与调参的过程复杂，使得时间复杂度较高[8]。而不同的应用场景需要对表情样本集进行在线再训练，以满足实时、高准确率检测的需求。相比较深度学习算法，经典算法的优点在于具有较低的时间复杂度，有着更好的实时性。因此本文选择在具有较低时间复杂度的经典算法基础上，针对特征提取过程进行改进，进而在保证实时性的前提下提高表情识别的准确率。其中PCA的特征提取和数据降维的能力尤为突出，是最常用的特征参数获取方法和降低数据维度方法[9]。PCA的基本目标就是用一组特征向量表征所获取的信息量，特征向量尽可能与初始信息相关联，从中获取主分量，保留了数据的最主要特征的同时还减少多余信息干扰。由于PCA算法操作简单，参量限制小，非常容易应用于特征场景中，被广泛地用于人脸表情识别当中。例如，文献[10]提出一种类内分块的PCA算法，对原始图像先进行分块处理，然后进行PCA特征提取。文献[4,11]将PCA算法分别和LDA算法和卷积神经网络算法相结合，进行特征提取。但是，在表情识别过程中由于个体不同而出现的表情差异及相似表情容易混淆的情况容易对主成分分析算法造成干扰。改进后的特征提取算法虽然在识别率上有所提高，但像类内分块PCA算法由于不同表情类别中块的大小会影响识别率，鲁棒性差。结合其他算法的新算法又会增加运行时间，实时性差。

为了解决上述问题，从而提升算法的识别准确率，同时保证算法的实时性，本文利用局部化思想[12-13]，提出一种用于人脸表情识别的局部主成分分析算法LPCA以及该算法的二维扩展，即二维局部主成分分析算法L-2DPCA。主要思想是为每个测试样本选取与其距离最近的部分训练样本作为新的训练样本集，该样本集通过突出不同训练样本类之间的差异，保证了在特征提取过程中与测试样本同一类别的训练样本在训练集中分类更准确，使PCA映射结果更准确体现测试样本的表情类别。

1　改进的面向人脸表情识别的L-2DPCA算法

1.1　PCA算法在人脸表情识别中的应用

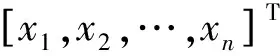
Step1获取训练样本矩阵。n幅人脸表情图片组成训练集x，每一幅表情图片xi的矩阵组成为D=p×q，样本矩阵表示如下:

x=[x1,x2,…,xn]T

(1)

Step2计算训练样本平均值，得到:

(2)

Step3计算第i个训练样本与平均值的差值，则有：

di=xi-φ

(3)

Step4计算协方差矩阵。协方差矩阵可以有效地度量表情特征之间的相关性。

(4)

Step5求协方差矩阵的特征值和特征向量，并构造特征空间。为了减少表情之间相关性造成的冗余信息，一般选取其中对人脸表情贡献率最大的m个特征值相对应的特征向量组成变换矩阵。

w=(u1,u2,…,um)

(5)

Step6将每一个训练样本与平均值作差，将得到的矢量投影到特征空间:

Ωi=wTdii=1,2,…,n

(6)

由此可以看出，PCA通过舍弃了数据中方差较小的方向，留下数据方差较大的方向，从而既保留了关键信息又减少了数据维数。接着用贡献率最大的m个特征带替原先的n个特征进一步减少了信息的冗余，该特征向量可以较大程度上代表表情样本的基本特征[15]。如果将表情图像投射到该特征向量空间，就能获取一组位置参数，即该表情图像所包含的数据都能够用这些基本特征的线性结合构成。

1.2　基于PCA改进的LPCA算法

PCA的实质就是在最大化保留表情样本特征的同时，将样本特征进行线性变换，映射到低维度空间中。但是，这种方法在识别表情过程中存在两个难点。首先，由于年龄、性别、地域、民族的不同会造成表情表达有所差异，主要体现在表情表达的强度和方式有所不同。例如：男性和女性在表达“悲伤”表情时，女性表达的强度可能会更强烈一些；年长者和年幼者在表达“高兴”表情时，年幼者可能表达的更加强烈；而不同地域不同民族的人在表达不同表情时表现的方式也会不同。其次，部分表情之间存在一定的相似性容易对识别造成干扰。例如：“生气”与“厌恶”，“惊奇”与“恐惧”，以及“悲伤”与“恐惧”是比较容易混淆的表情。其中“厌恶”与“生气”表情都出现了眼睑收紧和眉毛下压，“惊奇”和“恐惧”出现了上眼睑抬起，内外眉上扬，相反“悲伤”和“恐惧”都出现了眉毛下压和内眉上扬。

由于上述问题的存在，极易出现部分样本和其他类样本的距离，小于它与本类样本距离的情况，从而造成误判。如果只采用距离每个待分类样本最接近的N个训练样本，利用局部训练集，既能减少其他类别的干扰，也能减少相似的不同类样本出现的可能性，保证与待分类样本同一类别的训练样本在训练集中占更大比重，进而更能针对待分类样本的表情类别。

因此，本文提出了局部主成分分析算法，即LPCA。目的是提高PCA算法在表情相似性和表情个体差异干扰下的识别率和鲁棒性。其本质是在PCA算法基本步骤之前对训练样本进行甄选的过程，具体算法步骤如下：

Step1求训练样本的平均脸，即:

(7)

Step2将待分类样本Γ与训练样本的平均脸φ作差，将差投影到图像特征空间，得到其特征向量表示为:

Ω=wT(Γ-φ)

(8)

Step3求各个训练样本和训练样本平均值，两者作差得到平均脸差值矢量，并将得到的差值矢量投影到特征空间，计算:

‖Ωi-Ω‖i=1,2,…,n

(9)

Step4从中选择出前N个差值最小的训练样本，组成局部样本训练集；

Step5以局部样本集为基础进行PCA训练。

LPCA算法通过筛选出训练集的局部特征信息，使得测试样本的特征信息更准确地匹配到正确的表情类别。但是，它也有以下限制条件，首先，训练的样本类别必须大于1类；其次，为每个测试样本选择的局部样本数也应大于1，否则算法无解，极端情况下，每个待分类样本选择整个训练集作为“训练子集”，此时LPCA算法等价于PCA算法。

1.3　面向表情识别的2D-PCA算法

常用的一维主成分分析算法是一种以向量为基础的特征提取算法，就是在使用主成分分析算法前，将二维矩阵转化为一维矩阵，之后计算其特征值与特征向量。但是主成分分析的特征提取一直受限于计算量和复杂度，虽然奇异分解估计协方差可以降低计算量，但是估计协方差矩阵在样本过少时并不稳定，进而影响特征的提取。

在2004年Tang等学者对PCA进行了改进，首次提出基于图像的二维主成分分析2D-PCA(Two-Dimensional Principal Component Analysis)算法[16]。与主成分分析算法需要先将原始二维矩阵转化为一维矩阵不同，二维主成分分析算法直接处理二维矩阵，可以保留更多的空间结构信息，特征提取过程更加方便和直观[17]。其具体步骤如下[18-19]：

Step1假定表情图像D是p×q的二维矩阵，X则表示n维列向量，Y是经过线性的变换进行投影映射。

Y=AX

(10)

Step2Y是表情图像D经过投影之后的特征向量，最优的投影坐标轴X取决于投影之后Y的散度矩阵分布状况，而散度特征与相应协方差矩阵相关，计算如下：

J(x)=tr(Gx)

(11)

式中，tr(Gx)表示Gx的轨迹，Gx表示投影到特征向量空间的协方差矩阵。当J(x)=tr(Gx)获得最大值时，其物理意义为：寻求到一个投影坐标轴X，将训练样本投影在该轴，所计算出的特征向量矩阵的值最大。

Step3定义Y协方差矩阵如下：

Gx=E(Y-EY)(Y-EY)T

(12)

Gx=E[AX-E(AX)][AX-E(AX)]T

(13)

Step4定义Y的协方差矩阵的迹为总散度：

tr(Gx)=XT[E(A-EA)E(A-EA)]X

(14)

Step5定义表情图像D的协方差散度矩阵：

Gt=E(A-EA)T(A-EA)

(15)

Step6训练样本的均值图像为：

(16)

Step7训练样本数设为N，表情图像矩阵用Di表示，D表示训练的表情图像均值。记表情图像协方差矩阵为:

(17)

Step8将原式转化为：

J(x)=XTGtX

(18)

式中，当J(x)获得最大值时对应的X为最优投影轴。但是在样本类别较大的条件下，一个较优的投影坐标轴通常无法满足要求，因此需要去选择特征值最大的前N个特征值所对应的特征值向量构成向量，即

(19)

式中，Xi是比较大特征值所对应的向量，对于一个训练样本D，可以设定：

Yi=DXii=1,2,…,N

(20)

经过线性变换之后，可以得到一组向量Y1,Y2,…,YN，这组向量即为表情图像D的主成分分量。设2D-PCA算法中选择前M个向量组成特征矩阵，表情图像可以利用该特征矩阵YM进行描述，方便后续进行分类[20]。

1.4　基于2D-PCA改进的L-2DPCA算法

LPCA算法通过训练样本的预处理方式有效地减少样本分类误判的情况，但是同时由于样本的预处理计算过程，PCA只需经过N次循环即可选择出最佳的比例方案，而LPCA算法要求每个样本都经历N次循环，增加计算复杂度。根据对2D-PCA算法的深入研究可知，对于2D-PCA而言，不需要先把二维矩阵转化为一维矩阵，直接根据数据矩阵创建散布矩阵。一般来说，2D-PCA提取的特征比PCA更好更快，并且计算时间降低。因此，将2D-PCA算法结合到LPCA算法中，可以减少计算复杂度，提高时效性。与LPCA算法相似，L-2DPCA算法对于给定的每一个测试样本，选择与该样本拥有最近距离的前k个训练样本组成新的局部训练样本子集。具体步骤如下：

Step1假设训练样本集合如下，其中，i表示类别，j表示i类的j组数据。

(21)

Step2将待分类样本Γ与训练样本的平均脸φ作差，将差值映射在特征空间，求得特征向量为：

Ω=wT(Γ-φ)

(22)

Step3计算：

‖Ωi-Ω‖i=1,2,…,n

(23)

选择其中差值最小的N个训练数据样本，组成局部数据样本集：

(24)

Step4求取所有训练样本平均值：

(25)

Step5计算样本的协方差矩阵：

(26)

Step6求相应协方差矩阵，构造相应的特征空间：

U=(X1,X2,…,Xp)

(27)

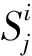
(28)

同样，在该算法过程中训练的样本类别必须大于1类，为每个测试样本选择的局部样本数也应大于1。

2　实验结果及分析

实验中的人脸表情样本是国际通用的Rafd表情库，以及通过摄像头采集的作者所在实验室LMIP表情库。为了避免数据的分布不均衡，选取图像过程中，令每种图像数据大小基本相同。在实验中的表情类别主要设为生气，厌恶、恐惧、高兴、悲伤、惊奇。在Rafd人脸表情库中选取6种基本表情，每种表情30张，在LMIP实验室图像库中选取男女比例大致相同的6种基本表情图像，每种表情各60张。由于LMIP为非标准表情库，所以要先对该库中的表情图像集进行规范化预处理，具体流程为：首先采用haar-adaboost方法提取图像集的人脸区域，接着对人脸图像集进一步进行归一化处理，得到50×50像素的标准人脸图像集，最后对标准图像集进行基于直方图均衡化的光照补偿处理，如图1所示。

图1　LMIP表情库样本图像和预处理后图像

实验中对预处理后的图像采用PCA方法，LPCA方法，2D-PCA方法和L-2DPCA进行进一步处理。表情特征提取算法性能的高低是借助表情分类准确率高低进行评估的。为了检验算法特征提取的精度，将本文中提出的LPCA及L-2DPCA算法与基线算法PCA和2D-PCA算法在同一个表情数据集合下进行比较，并且使用相同的训练测试方法及分类算法进行表情识别，从而控制实验结果仅与特征提取算法相关。本文选择最近邻算法为分类方法进行表情识别验证任务, 在实验中选用10折交叉验证的方式为测试方法来评估算法的准确率。实验结果如表1-表2所示。其中表1中的数据为在Rafd人脸表情库中各算法的识别准确率。表2中的数据为在LMIP人脸表情库中各算法的识别准确率。表中的算法耗时仅表示特征提取过程所用时间，单位为秒。表3给出了本文提出算法和当前几种主流算法的准确率对比数据。图2给出了Rafd表情库部分样本，图3是Rafd库中部分表情识别结果。

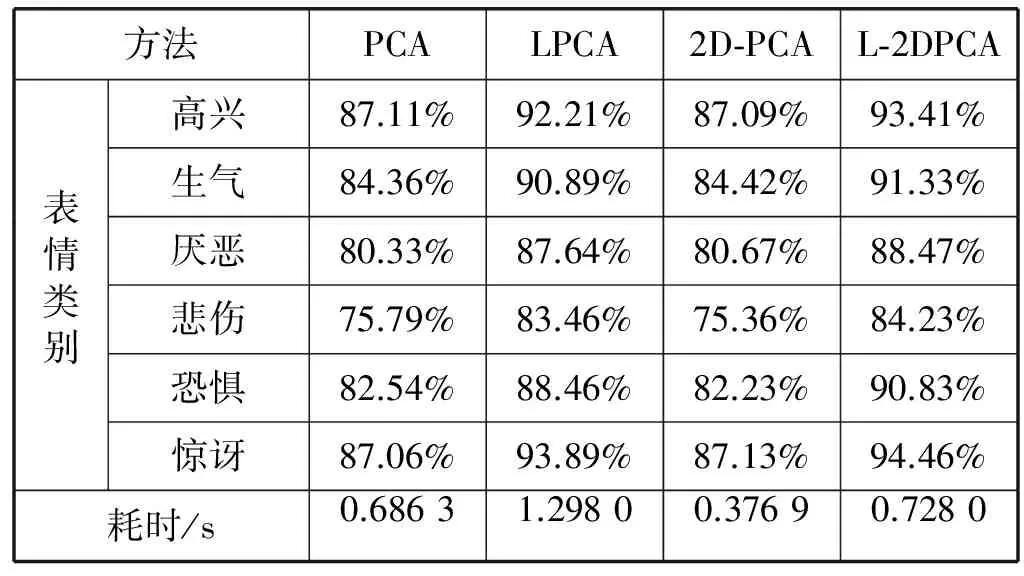
表1　Rafd人脸表情库中各算法的表情识别率

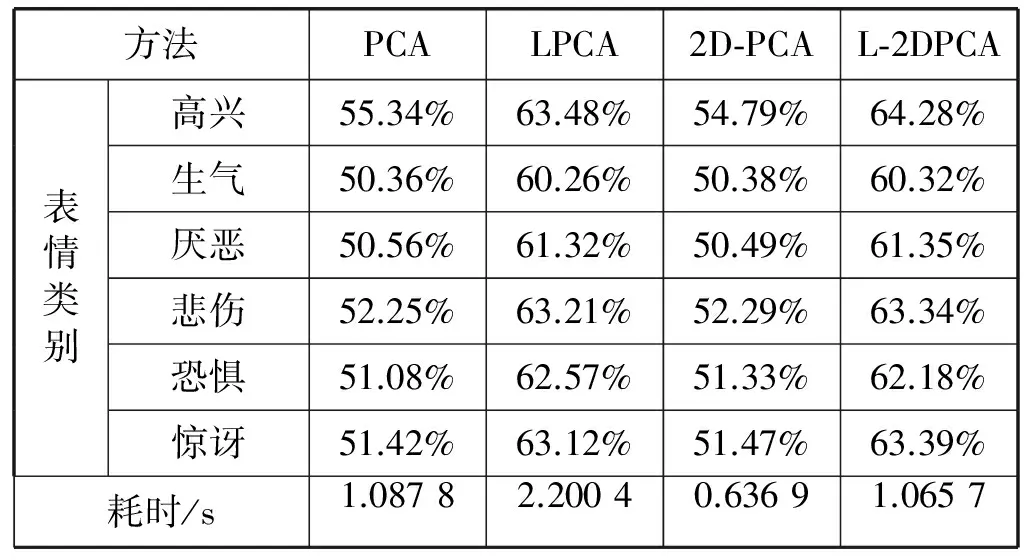
表2　MIP人脸表情库中各算法的表情识别率

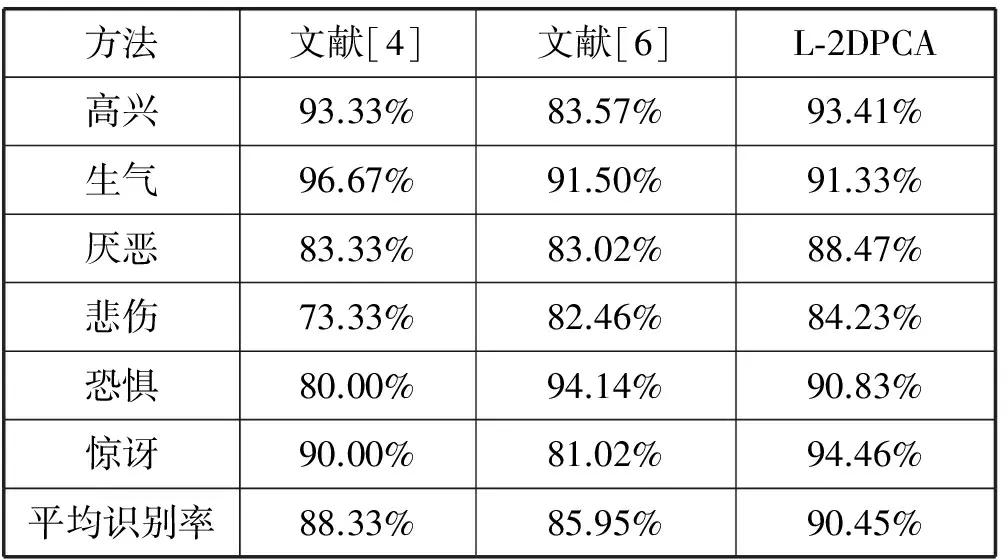
表3　算法比较

图2　Rafd表情库部分样本图

图3　Rafd库部分表情识别结果

实验结果证明在Rafd和LMIP人脸表情数据库中，本文所提出的LPCA及L-2DPCA算法与经典PCA算法相比较，明显提高了表情的识别率以及特征提取速度。在Rafd库进中，各个实验算法都获得很好的识别准确率。在LMIP人脸表情库中，由于数据库所录入的表情样本有较大的外貌差异,并且每个实验室同学对表情表达的强度也有较大的差异,导致最终识别率较低。但是在LMIP人脸表情数据库中，本文所提出算法仍高于经典算法，进一步说明了本文提出算法的鲁棒性。在两个人脸表情库中，可以发现LPCA相比PCA算法速度明显降低，2D-PCA相比PCA算法速度优势明显，而L-2DPCA与PCA相比较而言，算法速度基本一致。这说明引入L-2DPCA算法可以很大程度改善算法速度，克服LPCA算法速度慢的缺点，提高了表情识别的时效性。而在与现有主流算法对比过程中可以发现，可以看出本文提出算法在整体的准确率上有一定的优势。同时，在对不同表情的识别过程中可以发现，本文提出算法针对悲伤和厌恶这两类较为相似的表情有较好的识别结果，也说明了本算法的可行性。

3　结　语

本文在对PCA特征提取算法进行深入研究的基础上，主要针对表情识别过程中存在的由于个体不同出现的表情差异及相似表情容易混淆的问题，引入局部化思想，在PCA基础上提出一种针对表情识别的改进算法，即LPCA表情识别算法。LPCA的优点在于先根据待测样本与训练样本的距离选择与待测样本关系更为密切的训练样本作为局部训练样本，既能减少其他类别的干扰，也能减少相似的异类样本出现的可能性。但是由于每次识别样本都需要对训练样本与待测样本的距离进行计算，大大增加了特征提取过程的时间复杂度。因此本文结合2D-PCA时间复杂度低的优势，在LPCA的基础上，进一步提出L-2DPCA算法，经过算法对比实验验证，在运算时间和准确性上都取得了较好的效果。

[1] Ekman P, Friesen W V. Facial action coding system：atechnique for the measurement of facial movement[M]. Palo Alto Consulting Psychologists Press, 1978: 271-302.

[2] Shin M, Kim M, Kwon D S. Baseline CNN structure analysis for facial expression recognition[C]// Robot and Human Interactive Communication, 2016 25th IEEE International Symposium on, 26-31 Aug. 2016.

[3] 张韶旭. CNN深度学习模型用于表情特征提取方法探究[J].现代计算机(专业版), 2016(3): 41-44.

[4] 童莹. 一种方向性的局部二值模式在人脸表情识别中的应用[J].智能系统学报, 2015,10(3): 422-428．

[5] Zhang B, Liu G, Xie G. Facial expression recognition using LBP and LPQ based on Gabor wavelet transform[C]// IEEE International Conference on Computer and Communications. IEEE, 2017:365-369.

[6] 赵春伟. 基于PCA与LDA的表情识别算法研究[D].西安: 西安电子科技大学, 2014.

[7] 黄忠, 胡敏, 刘娟. 基于AAM-SIFT特征描述的两级SVM人脸表情识别[J].计算机工程与应用, 2016, 52(3): 178-183.

[8] 戴铂,侯志强,余旺盛,等. 快速深度学习的鲁棒视觉跟踪[J]. 中国图象图形学报,2016,21(12): 1662-1670.

[9] 陈伏兵, 高秀梅, 张生亮, 等. 基于分块PCA的人脸识别方法[J].计算机工程, 2006, 32(11): 231-233.

[10] 龚婷, 胡同森, 田贤忠. 基于类内分块 PCA方法的人脸表情识别[J].机电工程, 2009, 26(7): 74-76.

[11] 毛启容, 张飞飞, 于永斌, 等. 一种基于PCANet-CNN的任意姿态人脸表情识别方法: 中国, CN105447473A[P]. 2016-03-30.

[12] Shi Zhan, Hu Jinglu. Local linear discriminant analysis with composite kernel for face recognition[C]// Proceedings of International Joint Conference on Neural Networks. Piscataway NJ:IEEE Press, 2012: 1-5.

[13] Wang Zhan, Ruan Qiuqi, An Gaoyun. Facial expression recognition based on tensor local linear discriminant analysis[C]// Proceedings of International Conference on Signal Processing.Piscataway NJ:IEEE Press，2012: 1226-1229.

[14] Turk M, Pentland A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991,3(1): 71-86.

[15] Moon H, Phillips P J. Computational and performance aspects of PCA-based facerecognition algorithms[J]. Perception, 2001，30(3): 303-321.

[16] Chen S, Zhao H, Kong M, et al. 2D-LPP: A two-dimensional extension of locality preserving projections[J]. Neuro computing, 2007, 70(4): 912-921.

[17] Rajendran S, Kaul A, Nath R. Comparison of PCA and 2D-PCA on Indian Faces[C]// International Conference on Signal Propagation and Computer Technology, 2014: 561-566.

[18] 杨梅. 基于LBP和混合2DPCA+PCA的人脸识别研究[D].南京: 南京理工大学, 2007.

[19] 齐永锋, 火元连. 一种结合2DLPP与2DPCA的人脸识别方法[J].西南交通大学学报, 2011, 46(6): 910-916.

[20] Ip H H S, Yin L. Constructing a 3D individualized head model from two orthogonal views[J]. Visual Computer, 2013, 12(5): 254-266.