基于最优特征更新分类器的压缩跟踪算法
冷建伟 李 鹏
1(天津市复杂系统控制理论及应用重点实验室 天津 300384)2(天津理工大学自动化学院 天津 300384)
0 引 言
基于视频的目标跟踪是计算机视觉领域的一个重要分支。随着信息技术的发展,目标跟踪技术也越来越多的应用到现实生活中,给人们的工作和学习带来了难以想象的便利。同时,也带来了无限的商机和挑战,很多研究机构开始致力于目标跟踪技术的研究与应用。目前,虽然很多目标跟踪技术已经取得了成功应用,但当环境中影响因素较多时,跟踪准确性往往会降低。因此,如何降低干扰因素对跟踪的影响是计算机视觉领域一直以来的研究重点。根据检测过程与跟踪过程是否相关,可将跟踪算法分为生成式和判别式两大类。
生成式跟踪算法是从众多候选目标中寻找最优的候选目标,其跟踪过程与检测过程是相互独立的,二者有一定的先后顺序。2003年,Comaniciu等[1]利用目标颜色直方图建立表观模型,使用Mean-shift迭代求取最优解实现了目标定位。2012年,Rahmati等[2]对Comaniciu的方法进行了改进,实现了对婴儿四肢运动的跟踪。2004年,Li[3]提出一种具有较好鲁棒性的PCA算法,该算法使用子空间学习方法建立目标表观模型,在提高模型准确性的同时减少了算法耗时。2008年,Ross等[4]考虑到样本均值更新问题,提出使用增量在线更新样本均值,实现了表观模型的自适应更新。2009年,Mei等[5]利用稀疏约束优化重构系数,提高了目标模板重构性能,使跟踪稳定性有所提升。2011年,Li等[6]利用目标压缩特征建立目标表观模型,降低算法计算量,实现了对目标的实时跟踪。生成式跟踪方法利用目标表观模型跟踪目标,但这种方法容易受到背景干扰,特别是背景中存在与目标表观相似的物体时,容易跟丢目标。同时,由于视角、形态、光照等因素,实际跟踪目标往往没有确定的表观模型,很难对其进行结果性验证。
判别式跟踪算法充分利用背景信息,在跟踪过程中实时检测目标与背景,通过确定目标与背景的分界线进行分类,进而实现跟踪。2007年,Liu等[7]在Boosting框架下使用梯度特征成功构建了判别式表观模型,实现了目标与背景的分类。但该类算法没有根据特征之间的关系选取特征,导致所选特征重叠度较高,分类器更新比较单一。2011年,Babenko等[8]提出一种通过“包”的形式训练样本的多示例学习跟踪算法,使跟踪具有较强的学习和判别能力,但由于“包”中包含多个样本,使特征选择比较耗时,难以满足实时性。2012年,Zhang等[9]通过压缩感知理论降低样本维度,并使用朴素贝叶斯分类器对样本压缩特征进行分类,使跟踪具有良好的时效性。但该算法也存在一定缺陷:1) 跟踪过程中使用所有样本对分类器进行更新,分类器容易受到被污染样本的干扰,导致跟踪稳定性下降。2) 跟踪过程中始终使用固定尺寸的跟踪框检测和识别样本,当目标尺度变化较大时容易引进误差。为使跟踪具有更好效果,很多专家和学者改进了CT算法。2014年,毛征等[10]通过对样本压缩特征进行在线选择,提高了算法跟踪准确性,但没有解决跟踪窗口尺度问题。2016年,姜树明等[11]将Hog特征与多尺度矩形特征融合用于目标跟踪,并使用多样本矩形平均的方法确定目标位置,该算法跟踪稳定性高,不易受干扰影响,但提取目标多种特征比较耗时。同年,朱周元等[12]结合基于随机映射的外观模型以及粒子滤波方法,使算法能适应目标尺度变化,提高跟踪实用性。但该算法使用所有特征更新分类器,易受到被污染样本干扰。
本文在CT算法框架下进行改进,首先,对测量矩阵进行优化,提高测量矩阵压缩性能;然后,通过置信度和正负类分布差异对特征进行筛选,排除被污染样本影响,使分类器更新更加准确;最后,利用相邻两帧目标仿射变换使跟踪窗口可随目标尺度变化实时更新,减少采样误差,提高跟踪鲁棒性。
1 压缩跟踪算法简介
由压缩感知理论可知,通过使用稀疏矩阵R∈Rn×m(n< V=RX (1) 且当R满足Johnson-Lindenstrauss[13]准则时,V可最大限度的保留原始信号的判别信息。压缩特征由原始特征经稀疏矩阵获得,稀疏矩阵构造参考文献[9],即: (2) 式中:rij是稀疏矩阵的元素;s是[2,4]内随机生成的整数。 压缩跟踪算法中,特征提取过程如图1所示。首先,通过使用不同位置和大小的矩形滤波器对高维图像进行卷积,得到高维图像特征;然后,将高维图像特征归类为一个集合;最后,对该集合使用非常稀疏矩阵进行降维,得到样本压缩特征。 图1 特征提取过程 样本图像的低维特征向量v=(v1,v2,…,vn)∈Rn大体上服从独立分布[14]。因此,CT算法使用对满足独立分布变量误分率低且耗时小的朴素贝叶斯分类器对目标和背景进行分类,分类器模型如下: (3) 式中:y∈{0,1}为样本标记,y=1表示样本为目标,y=0表示样本为背景。 文献[15]证明了经稀疏矩阵投影得到的低维特征大体满足高斯分布,故H(v)中的条件概率p(vi|y=1)和p(vi|y=0)也服从高斯分布,即: (4) (5) (6) (7) 式中λ>0为学习率。 在压缩感知中,测量矩阵决定了原始信号的压缩与重构性能。好的测量矩阵需要满足一定的条件(例如:零空间特征、列相关、RIP等),在压缩时可保留原始信号的重要信息,并可以结合测量值重构原始信号。CT算法使用非常稀疏矩阵获取压缩特征,降低计算复杂度,但这种矩阵是一种随机矩阵,在应用上存在着一定的瓶颈:1) 随机矩阵元素由随机数构成,矩阵随机性比较大,导致跟踪结果重现难度大,且随机数依赖硬件产生。2) 随机矩阵很难完全满足RIP和弱相关条件,压缩性能并不是很理想。基于以上随机测量矩阵的不足,引入确定性测量矩阵。 压缩感知中确定性测量矩阵从构造角度可分为四类:1) 基于有限域的测量矩阵;2) 基于编码的测量矩阵;3) 基于训练的测量矩阵;4) 最大Welch界等式矩阵。由文献[16]可知,基于差集构造算法的最大Welch界等式矩阵满足RIP和列相干性条件,构造简单,压缩性能好,适用于跟踪算法。所以,本文使用基于差集构造算法的最大Welch界等式矩阵投影获取样本压缩特征。M×N维最大Welch界矩阵构造如下: (8) CT算法使用所有特征对分类器进行更新,当被污染或者不利于分类的特征用于更新分类器时,会影响分类器参数,进而影响跟踪性能。因此,选取优质的特征更新分类器是很有必要的。针对分类器更新问题,本文对一帧中提取的压缩特征进行两次筛选,使用置信度高且正负类分布差异大的特征更新分类器,提高跟踪抗干扰能力和准确性。 2.2.1初次筛选 初次筛选是通过置信度对特征进行筛选,置信度越高,表明特征包含目标信息越多;置信度越低,表明特征包含目标信息越少。为降低干扰影响,保证跟踪稳定性,要尽量使用包含目标信息多的特征更新分类器。本文使用径向对称的高斯核函数[10](最常用的径向基函数)来拟合特征置信度,其数学表达式为: (9) 式中:x为函数变量,xc为核函数中心,σ为函数宽度。函数值表示变量x到函数中心xc的欧式距离。 压缩特征服从高斯分布,因此可利用相邻两帧同一特征均值的差异来度量特征置信度,即: (10) 式中:μk+1是某一特征后一帧概率分布均值,μk是该特征前一帧概率分布均值。若得到函数值较大,则说明此特征在相邻两帧均值差异较大,特征很有可能遭到污染;若得到的函数值较小,则说明此特征在相邻两帧均值差异较小,包含目标信息较多。 在初次筛选阶段,首先利用式(10)计算同一特征在相邻两帧均值的差异,然后按得到的函数值大小对特征进行升序排列,选出前M个置信度高的特征等待二次筛选。通过使用置信度对特征进行筛选,可有效抑制由不良样本引入的噪声,降低对分类器选择的影响。此外,为了充分利用背景信息,不对背景进行置信度评价,而是随机选取负样本更新分类器。 2.2.2二次筛选 在CT算法中,分类器是通过寻找目标与背景的界限来分类的,特征正负类分布差异越大,目标与背景界限越明显,越有利于分类;特征正负类分布差异越小,目标与背景界限越模糊,越不利于分类。经过初次筛选以后,得到M个置信度高的特征,但由于这些特征正负类分布差异不同,所以分类能力也不同,因此,二次筛选的目的就是选取更利于分类的特征更新分类器。本文采用巴氏系数[17]度量特征正负类分布差异,对于连续分布,其表达式为: (11) 式中:p(x)和q(x)是两个样本,B∈[0,1]表示巴氏系数,可用来评价特征正负类分布差异。B越小,正负类差异越大;B越大,正负类差异越小。 在二次筛选阶段,首先计算经过初次筛选的M个特征的正负类分布差异,然后将特征按差异大小进行升序排列,选取前N(N CT算法在跟踪过程中始终使用初始跟踪框采集和检测样本,当目标尺度发生变化时,跟踪窗口不能很好的包围目标,易产生采样误差。为了避免采集样本带来的误差,本文通过求解相邻两帧目标仿射变换实时更新跟踪窗口。相邻两帧目标的仿射变换关系如下式所示: It=H×It-1 (12) 式中:It表示t帧目标,It-1表示t-1帧目标,H为3×3仿射变换矩阵,H可以表示为如下形式: (13) 式中:ρ是尺度因子,θ是旋转角度,(tx,ty)是平移向量。从上述公式可知,未知参数有4个,所以至少要存在4组匹配的特征点才能计算出仿射变换参数,而目标SIFI特征点可以提供多组(大于4)匹配特征。 跟踪窗口更新的步骤如下: (1) 提取初始帧目标SIFT特征点。 (2) 随机选取固定数目(大于4)的特征点,作为目标特征库。 (3) 从第二帧开始,提取当前帧目标SIFT特征点并与特征库中的特征点进行匹配,得到固定数目(大于4)的特征匹配组。 (4) 利用匹配的特征点求解目标仿射变换参数,更新跟踪窗口。 (5) 根据当前帧目标特征点更新目标特征库。 通过以上方式,获得相邻两帧目标的仿射变换参数,实时调整跟踪窗口尺度,防止目标尺度变化影响样本采集,使跟踪准确性和鲁棒性更高。 本文算法使用初始帧压缩特征构造分类器,对其他帧压缩特征进行分类,通过其他帧最优特征更新分类器,并根据目标变化实时更新跟踪窗口。算法流程如下: 2.4.1初始阶段 (1) 手工选取目标,设置初次筛选数目M,二次筛选数目N,初始特征置信度等。 (2) 根据目标位置和跟踪窗口尺度,分别采集正负样本图像集合Dα={z‖l(z)-l‖<α}和Dζ,β={z|ζ<‖l(z)-l‖<β},其中l是初始帧的跟踪位置,且α<ζ<β。 (3) 计算初始帧正负样本的多尺度矩形特征,使用基于差集构造算法的最大Welch界等式矩阵对样本投影得到压缩域特征。 (4) 利用初始帧压缩特征构造分类器。 2.4.2跟踪阶段 (1) 利用朴素贝叶斯分类器对上一帧压缩特征进行分类,得到目标位置。 (2) 使用目标仿射变换参数调整跟踪窗口大小和位置。 (3) 对上一帧压缩特征进行筛选,得到最优特征。 (4) 使用最优特征更新分类器参数,为下一帧做准备。 (5) 重复跟踪阶段的(1)-(4)进行连续跟踪。 为了验证本文算法性能,选取4个标准测试序列进行结果验证,并在测试过程中与CT和MIL算法进行对比。实验平台基于Windows7操作系统,采用VS2013+OpenCV2.4.9实现算法运行,主要参数设置如下:M=100,N=50,初始置信度为1,特征库中特征点个数为30,并从匹配的特征点中随机选取6组用于计算目标仿射变换参数。在跟踪过程中,采用中心误差(目标实际中心与跟踪结果中心之间的欧式距离)对跟踪精度进行定量评价。 Sylvester序列中,目标姿态多次变化,同时伴有光照和相似物干扰。由图2可知,当目标姿态小幅度变化时,三种算法跟踪都比较稳定;当#1040帧时,目标向左旋转并靠近光源,CT算法跟丢目标,MIL算法产生跟踪漂移;当#1306帧时,背景中存在相似物干扰,导致CT和MIL算法均产生较大漂移,而本文算法始终对目标进行着准确跟踪。可以看出,本文算法可有效抵抗光线、姿态、相似物等因素的干扰,抗干扰能力更强。 图2 Sylvester carScale序列中,目标尺度随序列越来越大。由图3可知,CT算法由于在跟踪中没有调整跟踪窗口,导致跟踪误差越来越大;MIL和本文算法可随目标变化实时更新跟踪窗口,但MIL算法以“包”的形式训练样本,跟踪窗口更新具有一定的不稳定性。而本文算法根据目标仿射变换更新跟踪窗口,使跟踪窗口可以很好的包围目标,满足多尺度跟踪要求,减少采样误差。 图3 carScale jogging序列中,目标存在遮挡影响。由图4可知,当#72帧时,跟踪目标完全被障碍物遮挡,三种算法都暂时失去目标;当#94帧时,遮挡物消失,目标重新出现,CT和MIL算法已将遮挡物误认为目标,导致跟踪失败。而本文算法可保留目标特征,当遮挡物消失后,可以重新定位目标,并对目标持续跟踪。 图4 jogging Freeman4序列中,目标在靠近镜头过程中伴随着左右旋转和遮挡等干扰因素,严重影响目标跟踪。由图5可知,当#0108帧时,由于目标左右旋转,CT和MIL算法出现了跟踪漂移;当#0262帧时,经过严重遮挡后,CT算法将遮挡物误认为目标,MIL算法跟丢目标。而本文算法能适应目标变化,始终对目标进行着有效跟踪。 图5 Freeman4 图6为中心误差曲线,是对跟踪精度的定量评价。由图6可知,与CT和MIL算法相比,在4个测试序列中本文算法具有最低的中心误差,在跟踪过程中,有效降低了光线突变、尺度变化、大面积遮挡等因素的影响,可对目标进行持续且稳定的跟踪。 图6 中心误差曲线 本文算法只使用部分优质特征更新分类器,间接降低了特征计算量。跟踪算法中特征计算次数如公式所示: N=m1×n1×NF+m2×n2×NF (14) 式中:m1为初次筛选候选特征,n1是初次筛选特征数目,m2为二次筛选候选特征,n2是二次筛选特征数目,NF为特征对应部分的计算次数。两种算法的特征计算次数如表1所示。由表1可知,本文算法所使用的特征数远小于CT算法所使用的特征数,因此,本文算法特征计算量也相应减少,提高了跟踪时效性。 表1 各算法计算次数及相关参数 次 为比较各算法运行速度,将每个序列测试20次,得出每一帧的平均处理时间,实验结果如表2所示。由表2可知,由于本文在线筛选特征和更新跟踪窗口,使算法耗时增加,但平均可达到27.57 ms/frame,满足实时性要求。 表2 各算法运行速度比较 ms/frame 本文提出一种基于最优特征更新分类器的压缩跟踪算法。首先,优化测量矩阵,提高测量矩阵压缩性能;然后,对压缩特征进行筛选,使用置信度高且正负类分布差异大的优质特征更新分类器;最后,针对跟踪窗口尺度问题,通过计算相邻两帧目标仿射变换实时更新跟踪窗口。实验结果表明,本文算法可有效抵抗光照、遮挡、尺度等因素的干扰,跟踪稳定性更高,鲁棒性更好,且满足实时性要求。与CT算法相比,虽然本文算法减少了特征计算量,但特征筛选和跟踪窗口更新还是比较耗时,使得本文算法在实时性方面与CT算法存在一定差距,如何减少耗时,将是本文后续研究重点。 [1] Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Ma-chine Intelligence, 2003, 25(5):564-577. [2] Rahmati H, Aamo O M, Stavdahl φ, et al. Kernel-based object tracking for cerebral palsy detection[C]//Proceedings of the 2012 International Conference on Image Processing ,Computer Vision, and Pattern Recognition (IPCV). United States: CSREA Press, 2012:17-23. [3] Li Y M. On incremental and robust subspace learning[J]. Pattern Recognition, 2004,37(7):1509-1518. [4] Ross D A, Lim J, Lin R S, Yang M H. Incremental learning for robust visual tracking[J].International Journal of Computer Vision, 2008,77(1-3):125-141. [5] Mei X,Ling H B.Robust visual tracking using l1minimization[C]//Proceedings of the 12th IEEE International Conference on Computer Vision. Kyoto, Japan: IEEE, 2009:1436-1443. [6] Li H X, Shen C H, Shi Q F.Real-time visual tracking using compressive sensing[C]//Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence,RI,USA:IEEE,2011:1305-1312. [7] Liu X M, Yu T. Gradient feature selection for online boosting[C]//Proceedings of the 11th IEEE International Conference on Computer Vision. Rio de Janeiro, Brazil: IEEE,2007:1-8. [8] Babenko B, Yang M H, Belongie S. Robust object tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011,33(8):1619-1632. [9] Zhang K H, Zhang L, Yang M H. Real-time object tracking via online discriminative feature selection[J]. IEEE Transactions on Image Processing, 2013,22(12):4664-4677. [10] 毛征, 袁建建, 吴珍荣, 等. 基于在线特征选择的实时压缩跟踪[J]. 光学精密工程, 2014,22(3):730-736. [11] 姜树明, 李凤娇, 张元元. 基于多特征融合的压缩跟踪算法[J]. 计算机工程与应用, 2016,52(15):203-207. [12] 朱周元, 张超, 吴小培, 等. 尺度自适应的压缩跟踪算法[J]. 计算机工程与应用, 2016,52(14):180-185. [13] Achlioptas D.Database-friendly random projection: Johnson-Linden straus with binary coins[J]. Journal of Computer and System Sciences, 2003,66(4):671-687. [14] Ng A Y, Jordan M I. On discriminative vs. generative classifiers: a comparison of logistic regression and naive Bayes[J].Proceedings of Advances in Neural Information Processing, 2002,28(3):169-187. [15] Diaconis P, Freedman D. Asymptotics of graphical projec-tion pursuit[J]. The Annals of Statistics, 1984,12(3):793-815. [16] 王强, 李佳, 沈毅. 压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报, 2013,41(10):2041-2050. [17] Comaniciu D, Ramesh V, Meer P.Real-time tracking of nonrigid objects using mean shift[C]//Proceedings of the 2000 IEEE Conference on Computer Vision and Pattern Recognition. Hilton Head Island, USA: IEEE, 2000, 2:142-149.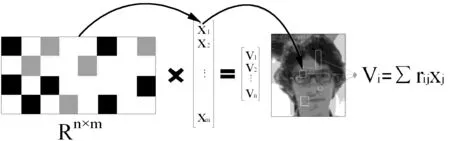

2 本文算法
2.1 优化测量矩阵
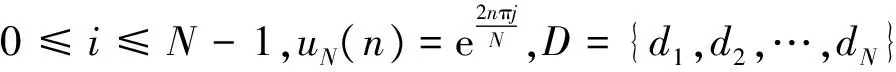
2.2 分类器更新
2.3 尺度更新过程
2.4 算法流程
3 实验结果及分析
3.1 准确性比较





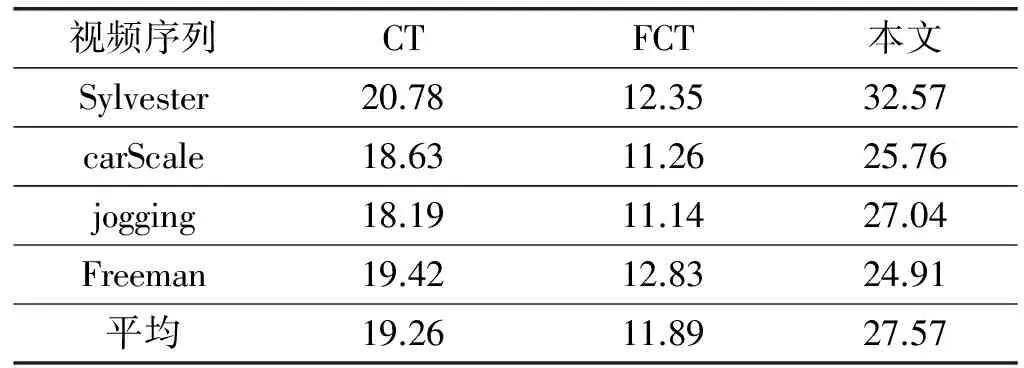
3.2 算法速度比较

4 结 语

