骨架算法在物料分选中的应用

李园芳　项　安

(同济大学电子与信息工程学院　上海 201804)

0　引　言

物料分选既是根据相应的要求或固定的标准将待分选物料分类成不同的产品或者剔除物料中的不合格品和异物，来提高其使用价值来满足消费和生产的需要[1]。在农业、农产品加工业、环境资源业、化工能源业等涉及天然性固体物料分级分类的各种领域中，物料分选得到了普遍应用[1]。在分选过程中，根据产品的外观特征参数(颜色特征和形状特征)要求作为分选依据。通常待分选物料中的不合格品以及异物的颜色特征与合格品没有明显的区分界限，因此形状分选在物料分选中起了重要的作用[2]。对于类似工业制品等完全按照严格的质量标准进行生产的物料，模板匹配算法就能达到较好的精度要求。但对于受自然因素、社会因素、生长规律等制约，具有某种程度的天然属性的物料(如农产品)，无与之匹配的固定模板。在色选和X射线异物检测等物料分选应用背景下，仅根据面积和周长等形状特征进行分选，往往漏检率较高[3]。因此，研究能够准确分选物料形状的特征是目前物料分选领域的热点。

骨架作为一种重要的图像目标形状特征，有效地反映出了物体形状的拓扑结构或连通性，是图像处理过程中许多特征提取的前提。骨架信息已经被广泛地应用在各个图像识别领域，在农业上，黄成龙等[4]应用玉米叶片骨架信息获取了叶片角度、长度和弯曲度性状，并且对叶片骨架基于位置的信息进行配准得到了单片叶性状的动态变化过程；刁智华等[5]提出了一种快速剔除伪分支的作物行骨架提取算法，基本满足了农业精准施药的要求；宗泽等[6]提出了基于骨架提取算法的作物表型参数提取方法，有效获得了玉米植株的平滑骨架图像；张天安等[7]提出了一种基Dijkstra距离分段的骨架提取方法，对树木主枝干进行了三维重建；罗艳等[8]提出了一种能够有效去除多余分支并且不影响主骨架线长度，完整地提取对虾主骨架线的算法。综上可见，骨架算法已被广泛运用于农业中叶片性状的测量、精准施药、树木三维重建等领域，但在物料形状分选中，骨架算法的应用研究较少。

本文对物料的二值化图像，利用骨架细化算法获得物料的骨架信息，通过对骨架信息的约束进行分选。为了进一步提高分选精度，对骨架信息进行了扩展应用，得到了物料的期望骨架长度，并且提出了新的基于骨架信息的圆形度和对称性算法。对所选的物料进行上述各项特征参数的判断，大大地提高了物料分选的精度。

1　骨架算法的原理及实现

1.1　骨架定义

骨架是可以反映物体形状的一组曲线，且其与原始形状拓扑结构分布和连通性具有一致性。骨架有两种经典定义：一种是草原之火模型，将一个图像区域想象为由干草组成的平坦大草原，且假设沿草原边界点火。火的前线以相同的速度向区域中心推进，中轴骨架就是同一时间多个火线到达点的集合[9]。

第二种经典的定义，即是最大圆盘定义，骨架就是最大圆盘圆心点的全数集合，最大圆盘就是指完全包含在物体内部，并且与物体的边界有两点或两点以上相切点的圆，每一个骨架点都是物体边界的一个最大内切圆的圆心点[9]。

另外，骨架的定义还有很多种，如形态学骨架、脊点投影骨架等。不论何种定义，骨架算法的基本原理即从物体的内部找到一组最大圆盘圆心点和相应的半径，利用这组数据来表示物体的形状轮廓，也可以通过这组数据实现物体形状轮廓的重建[10]。

骨架有许多性质[11]，如中心性、拓扑一致性、细性、等距变换不变性、可重建性、鲁棒性、光滑性等。

1.2　基于边缘点删除的骨架算法

目前主要有3类离散域骨架算法：一是拓扑细化的方法[12]，此方法可以保证得到骨架的连通性，但冗余的分支较多，对边界噪声非常敏感，且骨架点的位置并非准确地靠近物体的中心。二是基于距离变换的方法[13-15]，骨架是图像的距离梯度脊线，此类方法得到的骨架优点是位置精确，但连通性难以保证。三是基于Voronoi图的方法[16]。Voronoi图是中轴的包集，需要对生成的骨架进行修剪[17]，具有很高的复杂度。

上述几种骨架算法生成的骨架有各自不同的优缺点，但都需要大量的计算才能实现。为了改善计算效率，本文采用基于边缘点删除的骨架算法，该算法是迭代删除图像的边界点的细化算法，删除这些点时要服从如下约束条件：1) 不能删除端点；2) 不能破坏连接性；3) 不能导致区域的过度腐蚀[9]。

完整的骨架细化算法要经过多次相同步骤的迭代，其中每次的迭代都是由如下步骤组成：1) 标记将被删除的边界点；2) 删除做了标记的点；3) 在剩余的边界点中标记将被删除的边界点；4) 删除标记过的点。反复如上4个步骤，直到没有点被删除，此时算法终止，就得到了该图形的骨架[9]。上述4个步骤中，步骤1和步骤3的具体内容如下：

步骤1：首先假设区域点的值为1，背景点的值为0，参考图1的8邻域表示，定义边界点是值为1且至少有一个相邻像素的值为0的像素点。边界点p1如果满足如下条件，则将该边界点p1标为要删除的点[9]：

a) 2≤N(p1)≤6

b)T(p1)=1

c)p2·p4·p6=0

d)p4·p6·p8=0

其中，N(p1)是p1的非零相邻像素数量，即：

N(p1)=p2+p3+…+p8+p9

(1)

T(p1)是排序序列p2,p3,…,p8,p9,p2从0到1转换的次数。若p1点的8邻域中，p3,p5,p7,p8为1，其余为0，则N(p1)=4,T(p1)=3。

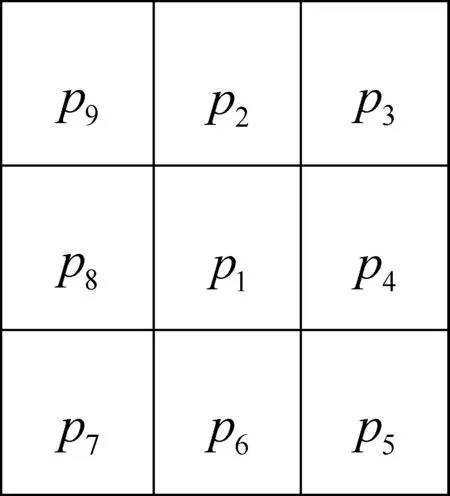
图1　邻域像素排列

步骤3：在判断某点是否被标记为被删除的点时，条件a)和b)与步骤1中的条件a)和b)相同，但条件c)和d)变为：

c′)p2·p4·p8=0,d′)p2·p6·p8=0。

2　骨架算法的应用

2.1　图像采集

本文以南瓜子为研究对象，采用X射线异物检测机获取南瓜子样本图像和常见异物样本图像，图片输出为16位灰度图像，如图2所示。用于图像处理的计算机配置为Pentium(R) Dual-Core, 2.60 GHz, 3.25 GB内存，并在Matlab R2012a软件中进行研究和开发。

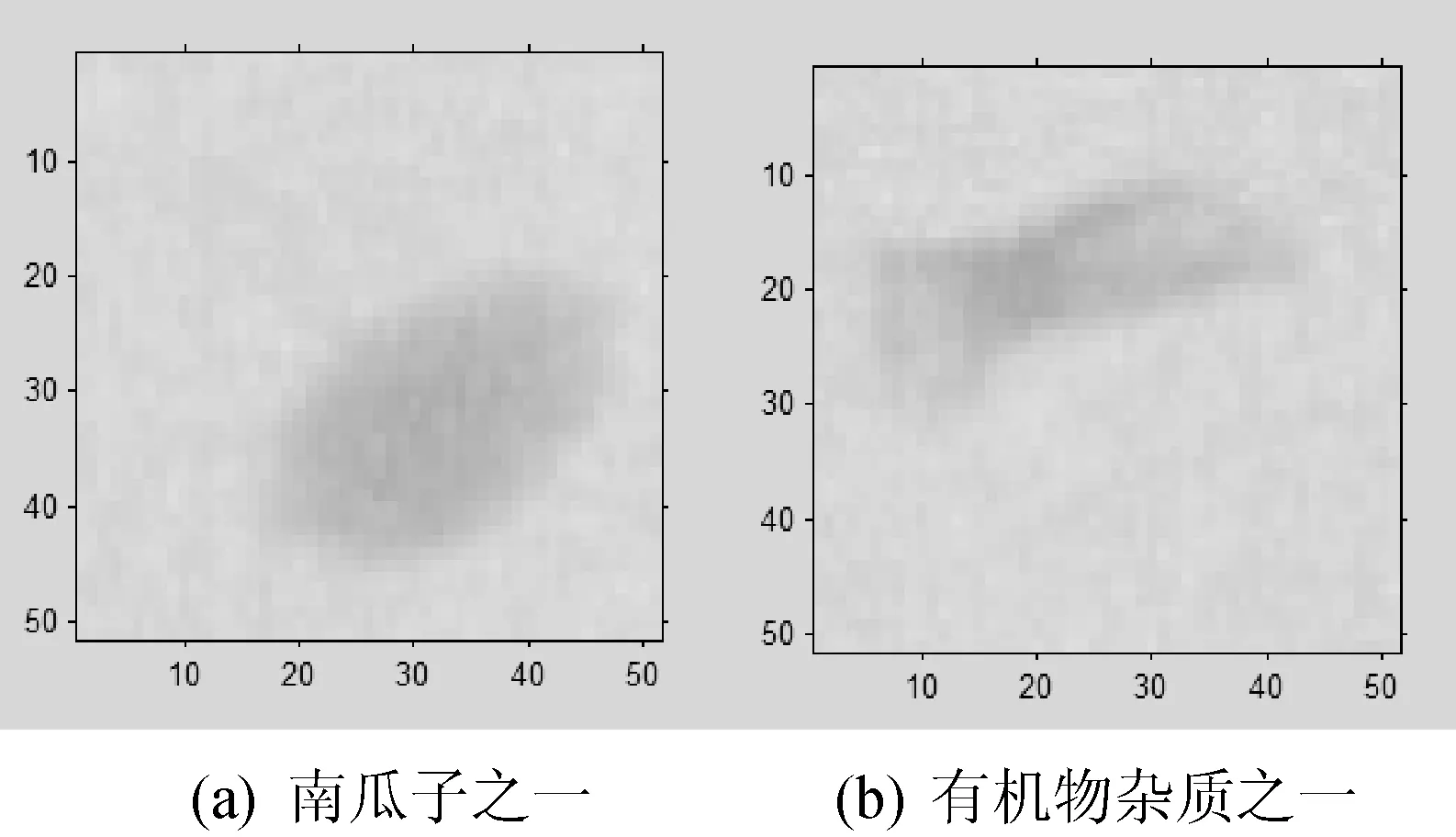
图2　X光机中得到的图像

2.2　图像预处理

通过对原始X光图像设定阈值，将物料和背景分开，得到二值化物料图像。由于X射线初始图像的背景中含有一些与物料颜色相近的像素块，阈值分割后的二值化图像存在噪声。通过形态学的腐蚀处理去除背景噪声，再通过膨胀处理得到边缘较为平滑的预处理结果图像。

2.3　期望骨架长度

采用本文所述基于边缘点删除的骨架算法对预处理结果图像进行骨架的提取，如图3所示。

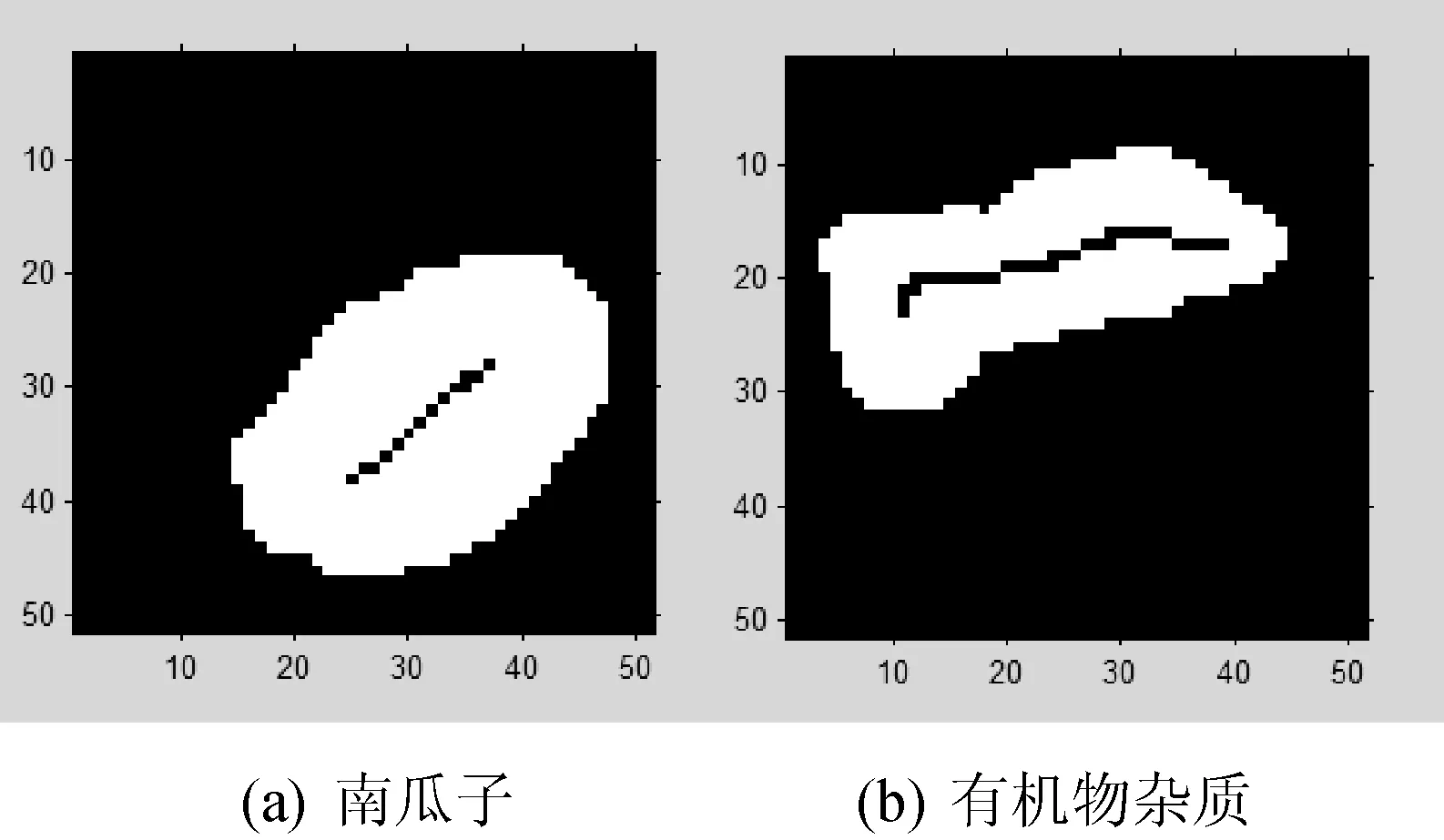
图3　初始骨架图像

合格的南瓜子产品外观形状多近似椭圆，因此合格产品的骨架多数为一条曲线。但由于南瓜子产品的大小不一(由采集的大量样本统计面积大小为250到800个像素点)，且由基于边缘删除的骨架算法的删除条件可知，对于越接近圆的图像提取的骨架越短(骨架端点距离初始边缘越远，见图4)，并不能直接根据该算法得到的初始骨架将合格南瓜子精确分选出来。基于此应用背景，本文对于基于边缘点删除的骨架算法得到的初始骨架进行改进与创新：

a) 简化骨架：去除初始骨架上的冗余点。

b) 沿简化后的骨架端点做切线交于原始边界，得到图像的期望骨架。

c) 计算期望骨架长度。

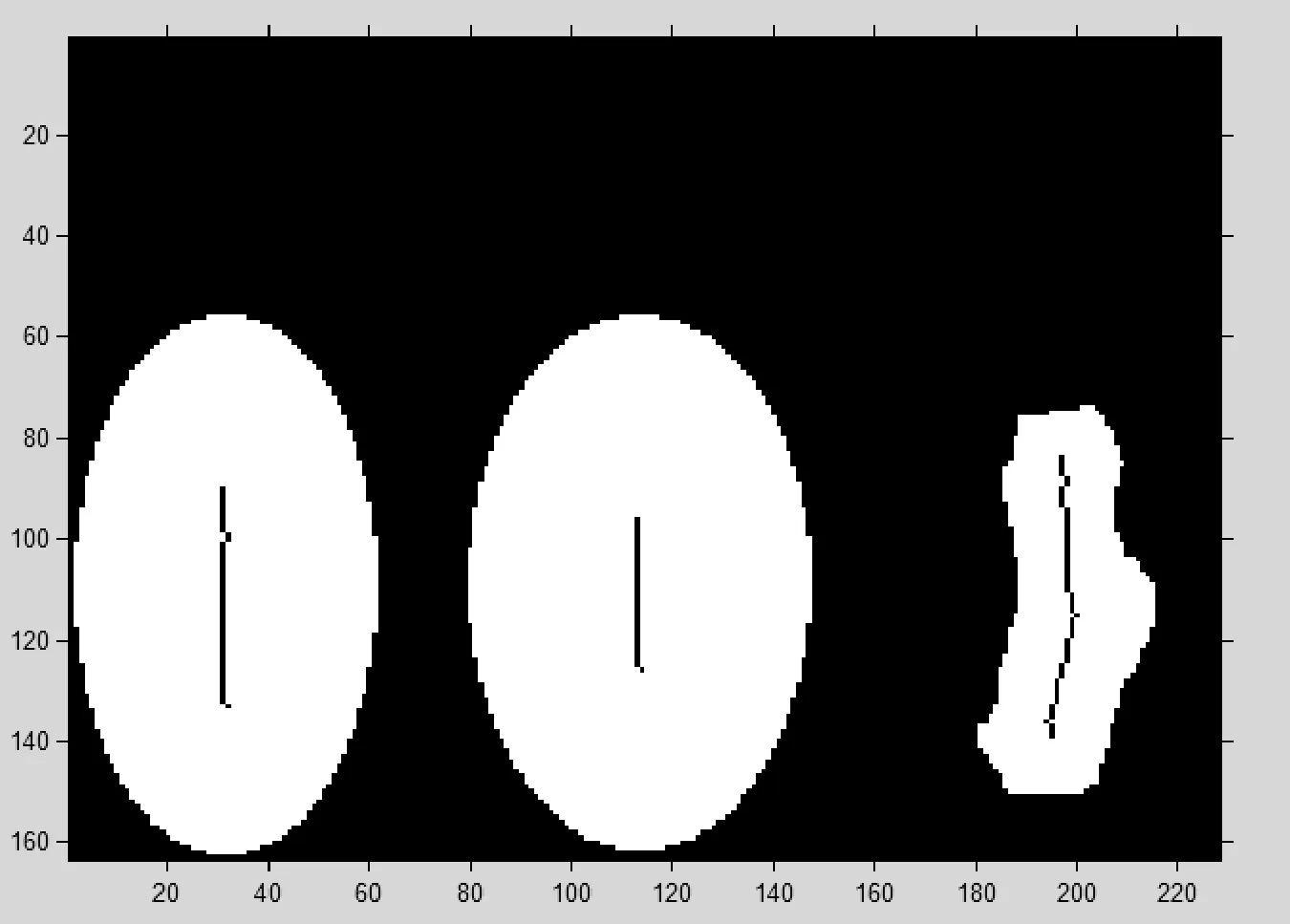
图4　骨架对比

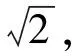
步骤二根据简化骨架的端点及其8邻域中的骨架点，以x=0,y=0的像素点为原点，得出切线的方程y=kx+b。此时切线与原始边界有两点相交，应当选择与此骨架端点距离最近的交点，初始骨架加上骨架端点与最近交点的连线就是本文所求的期望骨架。本文所选物料的骨架有两个端点，骨架端点与最近交点的连线也应有两条，如图5所示。

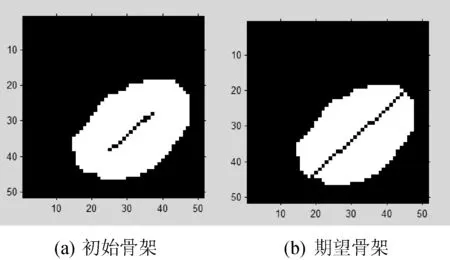
图5　期望骨架

步骤三计算期望骨架长度。计算排序后的相邻骨架点之间的距离，并将其相加。

2.4　圆形度

由于物料的期望骨架长度范围较大，仅根据长度进行形选精度仍不够高。本文提出圆形度来对物料进行分选，传统的圆形度计算等于4π乘以物料的面积与周长的平方之比[18]，亦或是通过计算物料的内、外切圆半径比值得到圆形度[2]。以上算法均需另求物料的周长参数或内、外切圆半径参数，本文则直接通过骨架长度来定义圆形度：

D=area/L

(2)

式中：area表示物料二值图像的面积，L表示期望的骨架长度。圆形度越高，表示物料越接近圆形，反之，物料形状越窄。

2.5　对称性

为了进一步提高形选的精度，本文引入对称性判断。南瓜子物料形状多近似为椭圆，几何意义上，椭圆中任何穿过中心点的直线相交于边缘的两点时，两个交点与椭圆中心点的距离相同。由于南瓜子图像并非处处对称并且为了提高算法的快速性，本文通过计算图像中四条穿过中心点的直线的对称性来判断物料是否为椭圆。对称性计算的重点是找到物料图像(即椭圆)的长轴，其余三条直线均可通过旋转长轴并且使旋转直线与边缘相交得到。传统的长轴计算方法均使用了最小外接矩形法，无论其如何优化，均需通过不断旋转图像，反复尝试才能得到图像的长轴和短轴[19-21]。此种方法运算量大，算法耗时，不符合物料形选时的实时性要求。本文利用骨架来快速判断图像中四条穿过中心点的直线的对称性。首先旋转物料图像使骨架处于水平0度方向并定义其为0度轴，逆时针方向旋转依次为45度轴、90度轴、135度轴，通过判断四条轴的边缘点与质心的距离之差，来判断对称性，具体步骤如下(其中各点标记情况见图6，假设图中椭圆为南瓜子物料的边缘)：

判断0度轴是否对称：

假设图7的直线AB是本文算法求得的骨架，计算得到骨架AB与Y轴的夹角θ，顺时针旋转θ度，求得旋转后图像中Y轴坐标与质心O点Y轴坐标y(o)相同的A点和B点的X轴坐标x(A)、x(B)，OA和OB的长度L(OA)、L(OB)分别为|x(A)-x(O)|、|x(B)-x(O)|。

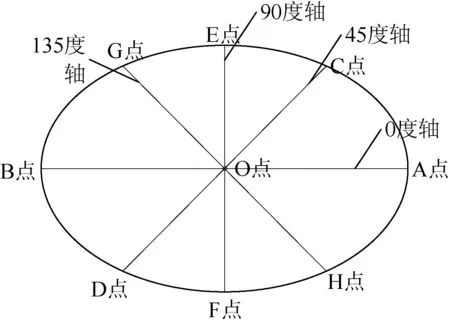
图6　对称性判断

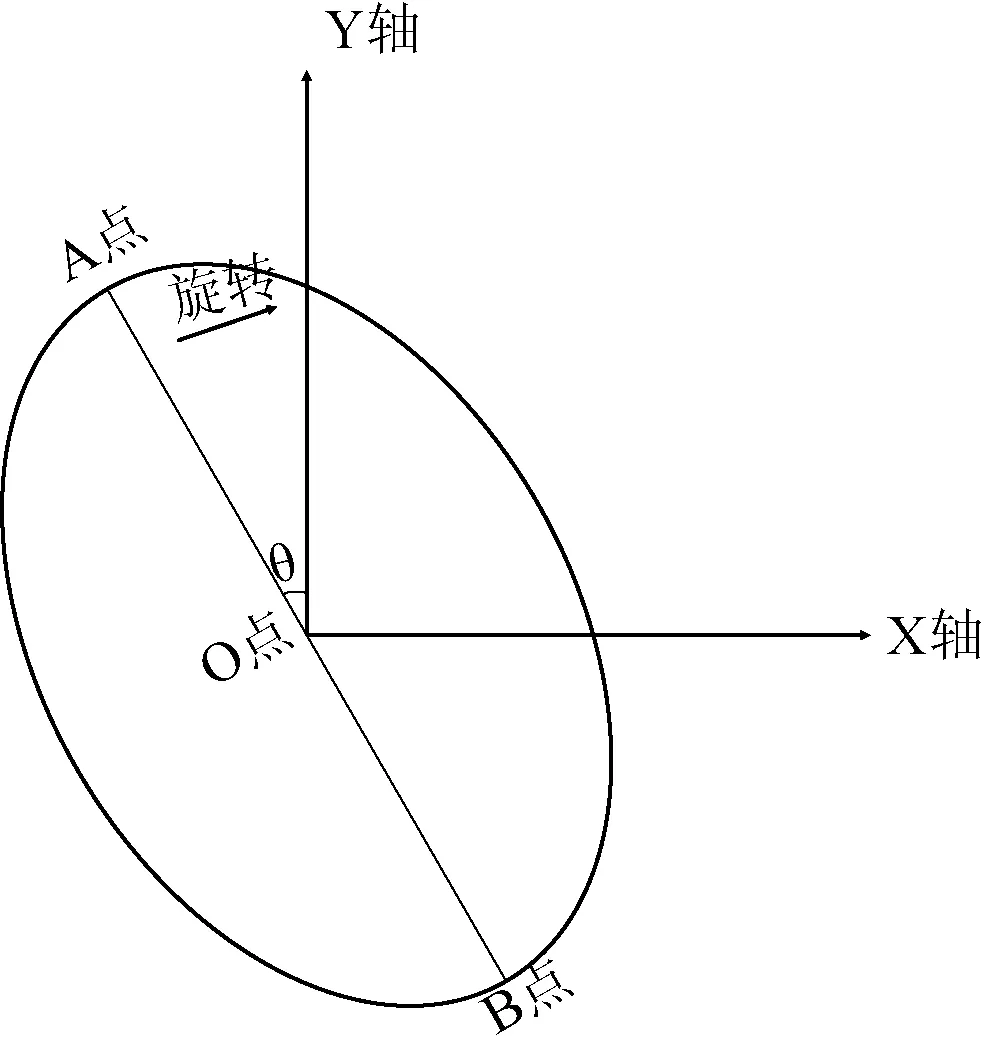
图7　旋转图形

若L(OA)与L(OB)长度之差小于4(实际南瓜子图形不一定为完全对称椭圆)，则本文认为O度轴对称，反之则不对称。45度轴、90度轴、135度轴判断方法与上述相同。当四个方向都轴对称时，则认为图形为对称。本文将物料的骨架信息直接运用到对称性计算方法中，不需要另外计算物料的长轴，算法简单快捷，满足了实时性要求。

3　实验结果分析

本文在X射线异物检测机上采集有代表性的36个南瓜子样本X射线图像和74个常见有机物异物样本X射线图像，如图8所示。样本图像中物料图像的不合格率为100%，使用MATLAB2012a作为图像处理工具。

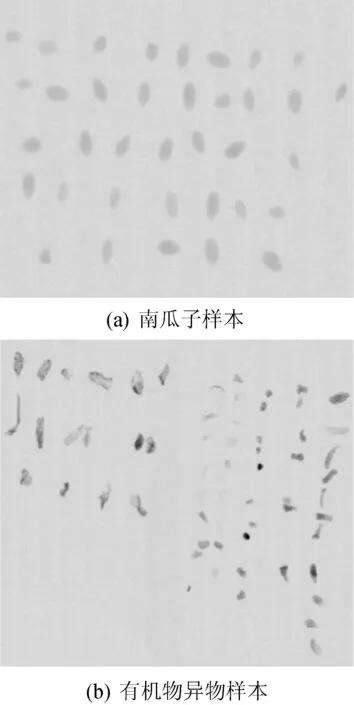
图8　样本图像

3.1　面积约束

先对样本图像进行二值化处理，提取图像中的物料区域。再对二值化物料图像进行形态学的腐蚀膨胀操作，得到预处理后的图像。统计南瓜子样本图像面积特征值，阈值范围为250～800。利用面积约束信息判断有机物异物样本，检测样本的不合格率为77%，与真实的不合格率100%有较大差距。

3.2　期望骨架约束

统计南瓜子样本图像期望骨架长度特征值，阈值范围为15～50。在面积约束的基础上，利用期望骨架长度约束信息判断有机物异物样本，检测样本的不合格率为84%，相比仅有面积约束条件时的检测精度得到了提高。

3.3　圆形度约束

选取一种传统的圆形度算法与本文所提基于骨架信息的圆形度进行对比，比较计算耗时以及其对检测精度的影响，见表1。

表1　圆形度算法比较

传统圆形度算法公式(物料周长用p表示)如下：

D=4π×area/p2

(3)

在实验条件下，增加两种圆形度约束，都提高了检测精度。其中，增加传统圆形度约束，检测精度比增加本文圆形度约束情况下高4%。但本文算法比传统算法耗时更少，出于在实际产品分拣过程中实时性的要求，本文选用了基于骨架信息的圆形度算法。

3.4　对称性约束

将基于骨架信息的对称性算法与基于最小外接矩形的对称性算法进行对比，比较计算耗时以及其对检测精度的影响，见表2。其中，基于最小外接矩形的对称性算法具体步骤如下：

1) 计算物料图像的质心，以及物体的边界。

2) 以质心为原点，将物体的边界以每次3°左右的增量在90°范围内旋转。每旋转一次都记录其坐标系方向上的外接矩形边界点的最大和最小x、y值以及外接矩形的面积。取面积最小的外接矩形的参数为长轴和短轴。

3) 将长轴逆时针旋转45度和135度求得物料图像的45度轴和135度轴，短轴作为90度轴。

4) 将求得的四根轴线与物料的实际边缘相交，判断物料图像是否在四根轴线上对称。

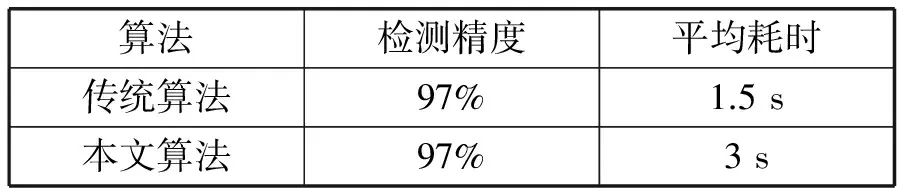
表2　对称性算法比较

在实验条件下，增加两种对称性约束，都提高了检测精度。但由于基于最小外接矩形的算法需要对图像进行30次旋转才能找到长轴，计算耗时较长。基于骨架信息的算法比传统算法耗时更少，检测精度较高，本文选用了基于骨架信息的对称性算法。

3.5　实验结果分析

增加了期望骨架长度、圆形度和对称性等三个骨架衍生的特征约束后，检测样本的不合格率为95%。相比仅做面积特征判断时，样本检测的精度有了很大的提高。并且基于骨架信息的圆形度特征算法和对称性算法与传统算法相比，不仅检测精度能满足要求并且实时性效果更好。

4　结　语

在物料的形状分选中，本文利用基于边缘点删除的骨架细化算法，获得物料的骨架信息。为了进一步提高分选精度，通过对骨架信息的扩展应用，得到了物料的期望骨架长度，并且提出了新的基于骨架信息的圆形度和对称性算法。在算法验证实验中，通过增加对物料的骨架信息以及衍生条件的约束判断，分选精度从77%提高到了95%。

本文提出了一种在无固定模板的物料的形状分选中，反映物料形状的连通性或拓扑结构并且有效提高分选精度的分选算法。该算法简单灵活，易于实现，能适用于多种类似的物料分选过程，满足了实时生产检测准确性要求，具有广泛的应用前景，但运算速度仍需进一步提高。

[1] 许万婷.物料分选的优化策略研究[D].大连理工大学,2013:1-2.

[2] 高达睿.基于颜色和形状特征的茶叶分选研究[D].中国科学技术大学,2016:1-3.

[3] 刘璎瑛.基于机器视觉的稻米品质评判方法研究[D].南京农业大学,2010:1-15.

[4] 黄成龙,张雪海,吴迪,等.基于时间序列的玉米叶片性状动态提取方法研究[J].农业机械学报,2017,48(5):174-178.

[5] 刁智华,吴贝贝,魏玉泉,等.一种快速剔除伪分枝的作物行骨架提取算法[J].农机化研究,2016(9):17-22.

[6] 宗泽,张雪,郭彩玲,等.基于骨架提取算法的作物表型参数提取方法[J].农业工程学报,2015(S2):180-185.

[7] 张天安,云挺,薛联凤,等.基于骨架提取的树木主枝干三维重建算法[J].南京师范大学学报(工程技术版),2014(4):51-57.

[8] 罗艳,张安红,成芳.基于机器视觉技术的对虾主骨架线提取[J].食品工业科技,2013,34(8):68-73.

[9] 阮秋琦.数字图像处理学[M].电子工业出版社,2013:525-527.

[10] 张静.骨架提取算法研究与应用[D].辽宁师范大学,2012:5-10.

[11] 黄文伟.基于拉普拉斯算子的点云骨架提取[D].大连理工大学,2009:9-13.

[12] Ogniewicz R L,Kübler O.Hierarchic Voronoi skeletons[J].Pattern Recognition,1995,28(3):343-359.

[13] August J,Zucker S W,Siddiqi K.Ligature Instabilities in the Perceptual Organization of Shape[C]//Computer Vision and Pattern Recognition,1999.IEEE Computer Society Conference on.IEEE,1999:2042-2048.

[14] Malandain G,Fernández-Vidal S.Euclidean skeletons[J].Image & Vision Computing,1998,16(5):317-327.

[15] Xie W,Thompson R P,Perucchio R.A topology-preserving parallel 3D thinning algorithm for extracting the curve skeleton[J].Pattern Recognition,2003,36(7):1529-1544.

[16] 丁颐,刘文予,郑宇化.基于距离变换的多尺度连通骨架算法[J].红外与毫米波学报,2005,24(4):281-285.

[17] 江萍,徐晓冰,方敏.基于形态学骨架提取算法的研究及其实现[J].计算机应用,2003,23(S1):136-137.

[18] 魏康丽,王振杰,孙柯,等.基于计算机视觉对苹果脆片外观品质分级[J].南京农业大学学报,2017,40(3):547-555.

[19] 向元平,何燕平,危郁林,等.一种快速提取植物叶片最小外接矩形算法[J].计算机与现代化,2016(2):58-61.

[20] 张法全,王国富,曾庆宁,等.利用重心原理的图像目标最小外接矩形快速算法[J].红外与激光工程,2013,42(5):1382-1387.

[21] 卢蓉,范勇,陈念年,等.一种提取目标图像最小外接矩形的快速算法[J].计算机工程,2010,36(21):178-180.