T型翼控制船舶在波浪上纵向运动的数值研究

孙一方 ，姜宜辰 ，2，3，宗智 ，2，3

1大连理工大学船舶工程学院，辽宁大连116024

2高新船舶与深海开发装备协同创新中心，上海200240

3辽宁深海浮动结构工程实验室，辽宁大连116024

0 引 言

高速船研究的瓶颈问题是，其在高速航行时受波浪影响较大，致使船体的垂向运动幅值过大，乘员晕船严重。为了控制高速船过大的运动响应，人们研制了不同的运动控制装置。近年来，T型翼因其体积小、效果明显而在高速船上得到普遍应用［1］。T型翼固定在船的艏部，通过随船运动产生升力，进而产生纵向矩，由此减小高速船的纵摇和垂荡运动，从而改善由垂向加速度引起的船上工作人员和乘客的晕船现象［2］，同时还可缓解大幅度的垂向运动对结构强度的冲击。将控制系统和传动装置引入T型翼减摇系统，可以使T型翼的摆角随着船舶的运动而改变，从而获得更大的纵向运动阻尼，提高减摇效果。

T型翼由水翼演变而来，最早出现于20世纪90年代，最初是固定在船底，很难安装和维修。90年代中期，美国的MDI公司和澳大利亚的INCAT公司联合研制了带有航态控制系统（RCS）的可回收式T型翼［3］并将其应用到了实船，经实践，发现可显著减少船的纵向运动响应进而改善船员的晕船情况；Fang等［4］针对SWATH船型，提出采用纵摇角速度信号控制稳定鳍的摆角来减小船在航行时的纵摇角。自2000年起，Cruz和Giron-Sierra等［5-6］将高速单体船加装T型翼和尾部副翼，利用计算流体力学（CFD）方法计算了不同海况和航速下裸船模型的水动力系数，并在此基础上构建波浪、力、运动之间的传递函数，继而引入T型翼的升力（矩）模型，利用动态系统仿真技术计算了引入主动控制的T型翼后船的运动响应，结果表明高速船运动时其垂向加速度可降低65%，晕船率可减少 35%［7］。2012 年，孔卫［8］基于切片理论对某深V型快速渡轮进行了水动力求解，其分别采用纵摇角速度信号和垂荡速度信号的控制策略实现了摆角在0°，15°和30°这3个值时的实时变化，并计算了航速在20和40 kn这2种控制策略下船的垂荡和纵摇响应。结果表明，采用纵摇角速度信号控制策略对纵摇角的减摇更为明显，而采用垂荡速度信号控制策略对垂荡运动的减摇更明显。刘冰［9］采用势流理论对某高速双体船进行水动力计算并构建了T型翼和扰流板的升力模型，在摆角的控制策略方面，利用仿真技术，采用纵摇角、纵摇角速度和纵摇角加速度联合控制的方式计算了减摇效果，结果表明，采用主动控制策略后，垂荡与纵摇的最大减摇幅值可达50%。

现有的研究对于加装主动控制T型翼后船在波浪上的运动响应的数值模拟大都是基于动态系统仿真软件，且对于T型翼摆角在不同控制信号下减摇效果的对比研究也较少。为此，本文将以某Wigley船型为研究对象，基于细长体理论计算在时域中不同航速下（Fr=0.3，0.5，0.65），不同波长规则波中运动的垂荡幅值、纵摇角和艏加速度；然后在此基础上对力矩控制策略进行讨论，采用纵摇角速度、角度和角加速度这3种信号分别对T型翼摆角进行控制，将T型翼产生的升力随时间的变化编入已有的细长体理论程序中，提出并计算3种控制策略下各信号的控制增益系数C；然后，将计算结果与无T型翼的裸船模的结果进行对比，得出不同信号单独控制T型翼摆角的减摇效果间的区别；最后，在单一信号控制的基础上初步研究3种控制信号联合控制时模型的运动响应，并与单一信号控制结果进行对比，为控制参数的进一步优化打下基础。

1 计算模型

根据细长体理论，对三维船体在波浪下的自由运动响应进行模拟。由于船舶的细长体特征，沿船长的速度分量远小于其他两个方向的分量，因而可将三维流体问题转化为一系列二维流体问题并通过边界元方法进行近似求解。在这种降阶方法中，将每个切片固定于某一空间位置，模拟船舶穿过此切片的过程［10］。通过将一系列的二维切片组合在一起，模拟三维船舶在波浪下的运动现象。

1.1 流场速度势及边界条件

设流体为不可压缩理想流体，忽略粘性的影响，流动的二维基本方程即为连续性方程和动量方程，如下所示：

式中：u为速度矢量；j为单位矢量；p为压力；g为重力加速度；ρ为液体密度。引入浮体和自由表面条件，考虑到入射波的影响，流函数ψ由位于复平面z=x+iy（其中x为复平面内的横坐标，y为复平面内的纵坐标，i为虚数单位）的复速度势β表示，包括入射波的复速度势β0和无旋复速度势βh两部分，有

式中：ϕ为流场内总的速度势；ϕh和ϕ0分别为由船体运动产生的速度势和入射波的速度势；ψh和ψ0分别为由船体运动产生的流函数和入射波的流函数。其中，β0用于模拟船体在规则波中以速度U航行时的迎浪环境，其速度势和流函数可由线性波浪理论求得；βh用于计算物体的辐射和自由表面的绕射问题，其值为本数值模型的求解项。计算模型如图1所示，图中，pex为施加于某一区域自由表面上用于造波的额外压强分布函数。βh的控制方程以及自由表面、物面及无穷远处的边界条件如下：

式中：∂Df，∂Db和 ∂DΣ分别为自由表面边界、物面边界和无穷远边界；w=u-iv，其中v为垂直方向速度；w*为复速度的共轭；x̌和y̌为某点在参考坐标系下的x和y的位置，分别为二维浮体的横荡、垂荡速度以及横摇角速度；nχ为船体表面某点的法向向量沿χ方向的分量。

本文提出的数值模型采用了一种虚拟的扩展速度概念，用来模拟船舶航速对二维平面流体的影响［11］。如图2所示，船舶在穿过某一固定平面时，与平面相切的船体轮廓会不断发生变化，当前时刻下物面上的流体微团会被推至下一时刻的物面上，以满足不可侵入条件。因此，船舶航速会诱发一个额外的速度，此速度所对应流函数的计算方法即为公式（7）中的最后一项。βh可通过建立柯西积分公式求解：

式中：∂D为计算域的边界；ζ为积分的虚拟变量。

1.2 三维船体的运动方程

由细长体理论可得三维船体在流场内的运动问题，可将其简化为一系列二维流体模型来近似求解。引入 3 个坐标系：大地坐标系 参考坐标系̂和动坐标系如图 3 所示，可得船体关于点的2个自由度的运动方程（本文只计算迎浪状态下的垂荡和纵摇运动）为

式中：mb为船体质量；γb为纵摇角；Ixx为关于点的纵摇转动惯量；为重心G在参考坐标系中的坐标；Fy为船体受到的垂向力；Mx为纵摇力矩。

船体受到的总的外力（矩）为各个分段受力的总和加上重力（矩）及其他作用力（矩），如图4所示。

式中：Li为二维计算平面在船体上的纵向位置；FT和MT分别为T型翼产生的升力和升力矩；F2，i为船体第i站受到的垂向力，可通过将每一站的湿表面的压力积分得到：

式中：ny为物面上单位向量沿y方向的分量；p为物面上承受的压力，表达如下：

1.3 船体和流体运动动态耦合的求解

为求解式（13）中的 ∂ϕh/∂t，文献［10］给出了求解方法。在船体表面 ∂Db上（图 1），为第i站参考坐标系原点在动坐标系下的垂直高度，∂ϕh/∂t的边界条件为

定义 2个新的复速度势函数［12］β2t和β4t，用来表示 ∂ϕh/∂t：

可知β2t仅与船体的加速度相关，令ϕ2和ψ2分别表示由船体加速度诱发的速度势和流函数，其边界条件为：

复速度势函数β4t的边界条件如下：

β2t和β4t可通过柯西积分定律进行求解。在此基础上，针对第i站定义参数A22，i和A42，i：

式中：A22，i为第i站水动力附加质量；A42，i为剩余流体动力和静力载荷的总和。ΔL表示相邻两站间距，有

将式（22）代入式（11），有

1.4 T型翼摆角的控制信号分析

船体以航速U在波浪中运动，A表示机翼平面形状的面积，式（23）中T型翼的升力FT和升力矩MT可由升力系数CL表示如下：

根据 López等［13］的研究，船舶在波浪上运动时，T型翼的攻角α由T型翼摆角φ、船的纵摇角γb以及船舶运动速度影响的一个附加角θF组成，即

其中，附加角受船舶垂荡速度ẏb、水翼面处波浪质点垂向速度ξ̇、纵摇角速度γ̇b以及航速U的共同影响，如图5所示。

由于θF为小量，可得

式中，lF为T型翼安装位置至船重心的距离。由于和ẏb两项相比较小，为计算方便，忽略其影响，且不考虑流场中存在的记忆效应，可得T型翼产生的升力（矩）为

水翼选定后，假设攻角|α|≤15°，则在某一特定航速下，为一常量，设为KF。

采用力矩控制的方式对T型翼的摆角进行实时控制，使其攻角与船在波浪上运动时的角位移量（包括纵摇角γb、纵摇角速度γ̇b、纵摇角加速度γ̈b）相反，以起到限制角位移的效果，继而减小船在运动时的纵摇、艏加速度和垂荡运动。

式中，C1，C2，C3为控制参数，其大小与船型、航速以及海况相关。联立式（27）和式（28），则有

于是，在确定了3种信号单独作用时相应的C值后即可得到T型翼摆角与船舶实时运动的关系。将式（23）和式（27）代入式（10），即可得到2个自由度的运动方程如下：

其中各系数的定义如下：

通过此显式方程，便可以在时域内求解船体的垂荡和纵摇加速度，然后再通过二次龙格—库塔方法获得船舶的速度和位移，最终得到船舶在迎浪下的垂向运动响应。

2 数值计算及结果分析

2.1 计算模型

计算采用Wigley III船型，其船型参数如表1所示。T型翼安装于船艏，距离艏柱0.2 m，参数如表2所示。Wigley III船型和T型翼的位置如图6所示。T型翼尺寸如图7所示。首先，用细长体理论计算3种航速下（Fr=0.3，0.5，0.65）不加水翼裸船模在规则波（波长λ=3，4，5，6，7 m）迎浪状态下，波高为0.021 4 m时的垂荡幅值、纵摇角值和艏加速度值。然后，引入T型翼升力的影响，采用单一信号控制和3种信号联合控制2种策略计算T型翼的减摇效果。

表1 Wigley III船型主尺度参数Table 1 Main dimensions of the Wigley III model

表2 T型翼尺寸数据Table 2 Dimensions of T-foil

对于单一信号控制的情况，假设采用角度信号控制T型翼的摆角，则令式（29）中的C2和C3为0，将先前计算的裸船计算结果代入摆角控制方程（29），调整C1值使得 -20≤φ≤20，便可求得C1值。同理，可确定其他2种信号单独控制时的C值，继而将3种控制信号分别与单独减摇作用后Wigley III船型的运动结果进行对比。

若采用3种信号联合进行控制，则将先前通过单一信号单独作用得到的C1，C2和C3值代入式（29）中，便可得到摆角φ随时间变化的曲线，然后将3个系数同时缩小相同的倍数以将摆角φ控制在同样的范围内，即-20≤φ≤20。表3所示为单独控制时各种工况下的C值。

表3 不同工况下控制参数Table 3 The control parameters of different conditions

2.2 单一信号控制下T型翼减摇的计算结果

在求得3种信号单独控制时的控制参数值的基础上，将加装T型翼后的Wigley III模型在不同工况下的垂荡幅值、纵摇角和艏加速度值进行比较，并分析不同控制信号减摇效果间的区别。

2.2.1 垂荡运动响应

3种航速下的垂荡运动响应曲线如图8～图10所示。图中，横坐标为遭遇频率ωe，纵坐标为垂荡幅值yb。表4～表6所示为3种航速下3种控制信号对于垂荡运动的减摇效果。

表4 Fr=0.3时的垂荡减摇效果Table 4 The effect of anti-heave motion when Fr=0.3

表5 Fr=0.5时的垂荡减摇效果Table 5 The effect of anti-heave motion when Fr=0.5

表6 Fr=0.65时的垂荡减摇效果Table 6 The effect of anti-heave motion when Fr=0.65

在低速情况下（Fr=0.3），裸船的垂荡峰值在波长λ=4 m处，此时采用角度信号进行控制具有最好的减摇效果，可达8.14%；在λ=3 m时，采用角速度信号控制的减摇效果最好，可达59.63%；随着波长的增加，3种控制方法对垂荡运动的抑制作用有所减弱，垂荡幅值在个别工况下甚至还有所增加。可见对于低速情况下的垂荡运动，T型翼仅在垂荡响应较小的情况下（λ=3 m）有积极的减摇效果，而对于其他响应较大的情况，减摇幅值在10%以内，效果并不理想。

随着航速的提高，在中速（Fr=0.5）情况下，裸船的垂荡峰值位于λ=4 m处，采用角速度信号控制时5个波长情况下的垂荡幅值均比无T型翼时更低，减摇百分比最大值位于λ=3 m处，达到了43.54%，峰值处的减摇效果为42.56%。随着波长的增加，减摇效果有所减弱，在λ=7 m时约降至5%。采用其他2个信号单独控制T型翼的摆角时，其对垂荡幅值的抑制作用均不如采用纵摇角速度信号控制时。

在高速（Fr=0.65）情况下，裸船的垂荡峰值位于λ=5 m处，此时采用角度信号控制T型翼的摆角具有最好的减摇效果，可达40.14%。在其他波长情况下，采用纵摇角速度信号控制减摇效果最为明显，在λ=3 m时可达78%。

总体上，在低速情况下，3种控制方式对垂荡的减摇效果并不理想。在中、高速的大多数情况下，采用纵摇角速度信号控制T型翼的摆角可以获得更小的垂荡幅值。

2.2.2 纵摇运动响应

3种航速下的纵摇运动响应曲线如图11～图13所示，其中纵坐标为纵摇角。表7～表9所示为3种航速下3种T型翼控制信号对纵摇角的减摇效果。

表7 Fr=0.3时的纵摇减摇效果Table 7 The effect of anti-pitch motion when Fr=0.3

表8 Fr=0.5时的纵摇减摇效果Table 8 The effect of anti-pitch motion when Fr=0.5

表9 Fr=0.65时的纵摇减摇效果Table 9 The effect of anti-pitch motion when Fr=0.65

在低速情况下（Fr=0.3），裸船模的纵摇角峰值出现在λ=3 m处，且随着波长的增加纵摇角逐渐减小。加入控制信号后，船的纵摇角均比无T型翼时小，在波长λ=3，4，5 m时采用纵摇角信号控制的纵摇角减摇效果最好，在峰值处减摇效果最多可达30.99%，其减摇百分比随波长的增加略有减小。其他2种控制信号下船的纵摇角变化趋势与裸船模大体类似。在λ=6，7 m时，采用纵摇角信号控制的船的纵摇响应最小，减摇效果维持在25%左右，而采用角加速度信号控制的纵摇响应和裸船模相比则有所增加。

在中速情况下（Fr=0.5），裸船模的纵摇角峰值位于λ=5 m处。加入控制信号后，在λ=3，4 m处，采用角速度信号控制T型翼摆角均可以起到相对积极的减摇效果，而采用其他2种信号控制时，在λ=3 m处均出现了响应增加的情况。在峰值处，采用纵摇角速度信号控制T型翼摆角的减摇效果最为明显，可达40.60%。在λ=6，7 m时，采用纵摇角信号控制T型翼的摆角可以获得更好的减摇效果，最多可达31.53%。

在高速情况下（Fr=0.65），裸船模的纵摇响应总体呈上升趋势，峰值位于λ=7 m处，此时按纵摇角速度信号控制对纵摇角的减摇效果最为明显，可达57.62%。与其他2种控制方式相比，采用纵摇角速度信号控制T型翼的摆角时船在5个波长下均有着更低的纵摇响应，而其他2种控制方式在个别波长时甚至出现了纵摇角明显增加的情况。

总体上，在低速情况下采用纵摇角信号控制可以更好地减少船的纵摇响应；在高速情况下，纵摇角速度控制信号对纵摇角的影响最为明显，且T型翼对纵摇角的减摇百分比也随航速的增加而明显提升。

2.2.3 艏加速度运动响应

3种航速下的艏加速度响应曲线如图14～图16所示，其中纵坐标为艏加速度a。表10～表12所示为3种航速下3种T型翼控制信号对艏加速度的减摇效果。

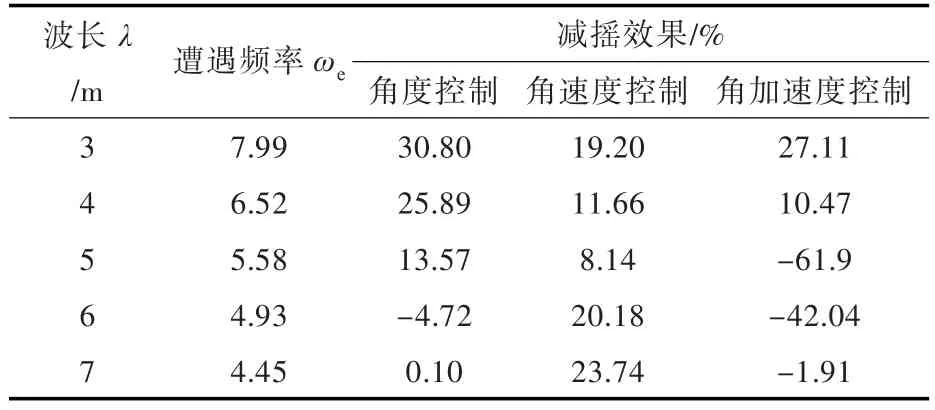
表10 Fr=0.3时的艏加速度减摇效果Table 10 The effect of anti-bow acceleration when Fr=0.3

表11 Fr=0.5时的艏加速度减摇效果Table 11 The effect of anti-bow acceleration when Fr=0.5

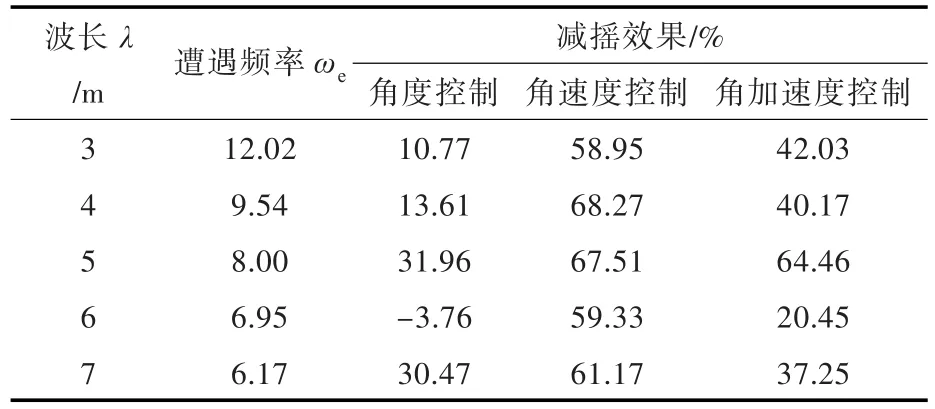
表12 Fr=0.65时的艏加速度减摇效果Table 12 The effect of anti-bow acceleration when Fr=0.65

在低速情况下（Fr=0.3），裸船的艏加速度随波长的增加而减小，峰值出现在λ=3 m处。加入控制信号后，在λ=3，4，5 m时采用纵摇角信号控制T型翼的摆角可以取得更好的减摇效果，其与裸船模相比在峰值处减摇效果可减少30.8%。随着波长的增加，减摇效果递减，当λ=6，7 m时，采用角速度信号控制T型翼的摆角减摇效果最多可达23.74%，而其他2种控制信号则并不能有效减摇。

在中速情况下（Fr=0.5），裸船的艏加速度峰值位于λ=5 m处，此时采用角速度信号控制T型翼的摆角可以获得更好的减摇效果，可达33.47%。在λ=3 m时，采用角速度和角加速度信号控制的减摇效果差别不大，明显好于采用角度信号控制的；λ=4 m时，采用角加速度信号控制的减摇百分比略优于其他2种，最多可达55.99%。随着波长的增加，在λ=6，7 m时，采用纵摇角速度信号控制T型翼摆角的减摇效果明显好于其他2种信号控制。

在高速情况下（Fr=0.65），裸船的艏加速度响应峰值出现在λ=7 m处，此时采用角速度信号控制T型翼的摆角可以获得最好的减摇效果，最多可达61.17%；在其他波长情况下，采用角速度信号控制后船的艏加速度也优于其他2种控制方式，减摇百分比最多可达68.27%。

总体上，采用角速度信号控制T型翼的摆角在各个情况下对艏加速度都可起到积极的抑制作用，且其减摇百分比受波长影响较小，而其他2种信号控制则只在中速和低速的个别波长下有着更为积极的减摇效果。

2.3 联合控制下T型翼减摇的计算结果

在单一角位移信号控制的基础上，对多信号联合控制T型翼摆角的方法进行了初步探索，并计算了其对Wigley III船型的垂向运动减摇效果，旨在为下一步的研究打下基础。图17和图18所示为采用3种角位移信号联合控制与采用单一信号控制T型翼摆角后的减摇效果，其中单一信号控制下模型的垂向运动响应选取的是每种工况下减摇百分比最大的信号作用结果。由图可见，在运动响应较大的区域，采用混合信号控制后模型的垂荡幅值与单一信号控制时相比明显偏大，而在响应较小的区域，2种控制方法下的垂荡幅值区别较小。对于纵摇运动，在λ=3，8 m以及响应较低的区域，混合信号控制下模型的纵摇角与单一信号控制下相比略有减小，但是在纵摇角较大的区域，采用混合信号控制时其响应均比单一信号控制时有明显的增加。

3 结 论

本文采用细长体理论方法计算了Wigley船型在规则波上的运动，并分别采用纵摇角、纵摇角速度和纵摇角加速度3种不同的信号控制T型翼摆角，计算了加装T型翼后其减摇效果的提升，并在此基础上计算了3种信号联合控制T型翼摆角的减摇效果，得到如下结论：

1）对于Wigley船型，在不同的波长和航速下，控制参数的值有所不同。若采用单一信号控制T型翼的摆角，当Fr=0.3时，对于模型垂荡幅值的减摇，在波长小于2倍船长时采用纵摇角信号控制可以在响应峰值处获得最好的减摇效果，而在其他波长时3种控制策略均无法有效减摇；对于纵摇角的减摇，采用纵摇角信号的控制策略对T型翼摆角在各个波长下均有更好的减摇效果；对于艏加速度的减摇，在波长小于2倍船长时采用纵摇角信号控制减摇效果最好，而在其他波长时则应采用纵摇角速度信号控制T型翼的摆角。总体上，当Fr=0.3时采用纵摇角作为T型翼的控制信号可以在低速下获得更好的减摇效果。

2）当Fr=0.5时，采用纵摇角速度信号控制T型翼的摆角对垂荡幅值的减摇效果最为明显，最大减摇百分比可达43.54%，峰值处为42.56%；对于纵摇角的减摇，在峰值处采用纵摇角速度信号控制减摇效果最好，可达40.60%，在波长不小于2倍船长时采用纵摇角信号控制T型翼的摆角减摇效果更为理想；对于艏加速度的运动响应，采用角加速度信号控制在λ=3，4 m处具有最大的减摇百分比，在其他波长，包括响应峰值的情况下，采用纵摇角速度控制具有更为明显的减摇效果。总体上，在Fr=0.5的情况下，采用纵摇角速度作为T型翼摆角的控制信号可以在多数波长下获得更好的减摇效果。

3）当Fr=0.65时，对于垂荡运动，在响应峰值处采用纵摇角信号控制减摇效果最好，在峰值以外的其他情况下采用纵摇角速度控制策略减摇效果更好；对于纵摇角和艏加速度，采用纵摇角速度信号控制T型翼的摆角减摇效果更好，而其他2种控制信号均在个别波长出现了运动响应增加的情况。在高速情况下，T型翼的减摇百分整体上也明显高于中、低速。

4）与单一信号相比，在垂向运动响应较低的波长下，采用混合信号控制T型翼的摆角可以略微提高T型翼的减摇效果，但在响应较高的区域，采用单一信号控制可以获得更低的运动响应。混合控制参数计算较单一的信号控制更为复杂，本文只进行了初步的分析讨论。

本文在计算T型翼产生的升力矩时并未考虑T型翼与船底的作用，且忽略了流场中的记忆效应，后续的研究将对混合控制的参数计算进行优化并计算其对某典型船型垂向运动的减摇效果。

参考文献：

［1］DAVIS M R，WATSON N L，HOLLOWAY D S.Wave response of an 86 m high speed catamaran with active T-foils and stern tabs［J］.Transactions of the Royal In⁃stitution of Naval Architects Part A：International Jour⁃nal of Maritime Engineering，2003，145（A2）：15-34.

［2］FANG C C，CHAN H S.An investigation on the verti⁃cal motion sickness characteristics of a high-speed cat⁃amaran ferry［J］.Ocean Engineering，2007，34（14/15）：1909-1917.

［3］HAYWOOD A J，DUNCAN A J，KLAKAK P，et al.The development of a ride control system for fast ferries［J］.Control Engineering Practice，1995，3（5）：695-702.

［4］FANG M C，SHYU W J.Improved prediction of hydro⁃dynamic characters of SWATH ships in wave［J］.Pro⁃ceedings of National Science Council，1994，18（5）：495-507.

［5］CRUZ J D L，ARANDA J，GIRON-SIERRA J M，et al.Improving the comfort of a fast ferry［J］.IEEE Control Systems，2004，24（2）：47-60.

［6］GIRON-SIERRA J M，ESTEBAN S.Frequency do⁃main study of longitudinal motion attenuation of a fast ferry using a T-foil［C］//Proceedings of the 17th IFAC World Congress.Seoul：IFAC，2008：15004-15009.

［7］ESTEBAN S，GIRON-SIERRA J M，DE ANDRES-TO⁃RO B，et al.Fast ships models for seakeeping improve⁃ment studies using flaps and T-foil［J］.Mathematical and Computer Modelling，2005，41（1）：1-24.

［8］孔卫.船舶在纵向波浪中运动控制方法研究［D］.武汉：华中科技大学，2012.KONG W.Investigation on the control method of ship motion in longitudinal waves［D］.Wuhan：Huazhong University of Science and Technology，2012（in Chi⁃nese）.

［9］刘冰.高速双体船纵向运动及其控制研究［D］.哈尔滨：哈尔滨工程大学，2012.LIU B.Study of longitudinal motion and control of high speed catamaran［D］.Harbin：Harbin Engineering Uni⁃versity，2012（in Chinese）.

［10］YEUNGR W，JIANGY C.Bilgekeel influence on the free decay of roll motion of a three-dimensional hull［C］//Proceedings of the 33rd International Confer⁃ence on Ocean，Offshore and Arctic Engineering.San Francisco：ASME，2014.

［11］YEUNG R W，KIM S H.Radiation forces on ships with forward speed［C］//Proceedings of the 3rd Inter⁃national Conference on Numerical Ship Hydrodynam⁃ics.Paris：Palais des Congres，1981：499-510.

［12］JIANG Y C，YEUNG R W.Computational modeling of rolling wave-energy converters in a viscous fluid［J］.Journal of Offshore Mechanics and Arctic Engi⁃neering，2015，137（6）：061901.

［13］LÓPEZ R，SANTOS M.Neuro-fuzzy system to control the fast ferry vertical acceleration［C］//Proceedings of the 15th IFAC World Congress.Barcelona：IFAC，2002：319-324.