基于描述函数法的滚动通道自持振荡研究*
廖幻年,金一欢,彭继平,刘 露,田 野
(上海航天控制技术研究所·上海·200233)
0 引 言
舵机作为飞行控制系统的执行机构,其功能是根据控制系统给出的舵指令,控制舵机转动,产生相应的操纵力矩,从而控制导弹进行机动飞行。舵机的工作特性直接影响飞行控制品质。工程师根据飞行控制要求,给舵系统提出频率特性、最大舵偏角、最大舵偏角速度等性能指标。实际上,舵系统受设计、生产、加工等多个环节的影响,存在非线性环节,如死区、饱和、间隙等。这些非线性特性常导致飞控系统产生稳态误差和极限环振荡,特别是当滚动通道舵效率过大导致控制精度较低时,非线性特性带来的极限环振荡较为明显,甚至影响飞控系统的稳定性[1-7]。
针对舵系统非线性带来的极限环振荡,基本都是从舵系统本身层面展开分析,例如多名学者提出了将非线性补偿的概念应用于舵系统控制器设计,实现非线性补偿[8-9],然而非线性补偿的方法工程应用较为困难。本文从飞行控制系统的层面,针对舵系统非线性,应用描述函数法,对飞控系统滚动通道极限环振荡特性进行了研究,并给出了相关结论。
1 滚动通道数学模型
飞行器滚动通道小扰动线性方程为[10]
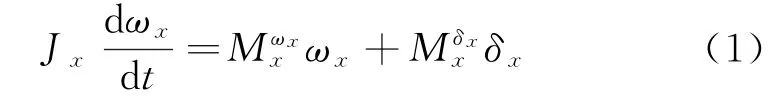
式中,Jx为飞行器沿纵轴的转动惯量;δx为副翼的偏转角。
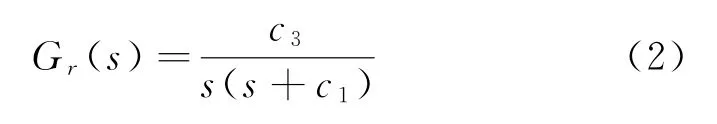
滚动通道采用传统的PD线性控制方法,得到滚动通道控制系统结构图如图1所示,图中舵系统由线性部分Gw(s)和非线性部分f组成。
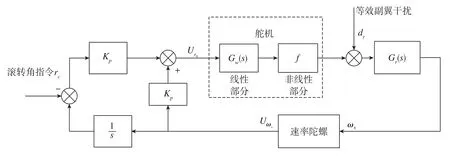
图1 滚动通道控制系统结构图Fig.1 Structure diagram of the roll channel control system
2 舵机非线性的描述函数分析法
舵机模型由一个典型二阶线性系统和非线性系统组成,假设舵机的线性部分等效二阶模型为

其中,ωn=80rad/s,ξ=0.7,剪切频率为13 Hz。
舵机的非线性包括死区、饱和、间隙和摩擦等,工程实践发现舵机的间隙是滚动通道发生极限环振荡的主要原因,本文就间隙进行具体分析。
描述函数法是分析非线性系统的基本方法[11],其基本思想是:当系统满足一定的假设条件时,系统中非线性环节在正弦信号作用下的输出可用一次谐波分量来近似,由此导出非线性环节的近似等效频率特性,即描述函数。用描述函数法研究非线性系统时,需要被研究系统满足以下假设条件:1)只有一个非线性环节;2)非线性环节时不变;3)非线性环节N对应于正弦输入,只考虑输出的激波分量;4)非线性特性关于原点对称。分析可知舵系统的间隙环节满足以上4个假设。
以下利用描述函数法对间隙特性进行具体分析。间隙特性的数学描述如下所示:
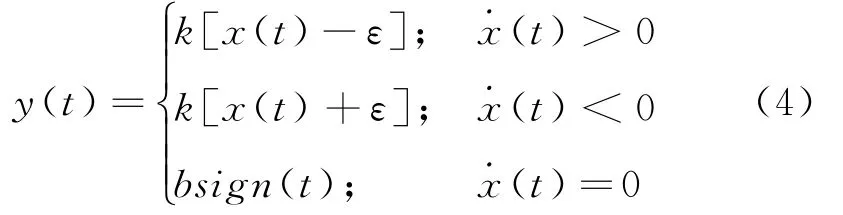
间隙特性的描述函数为
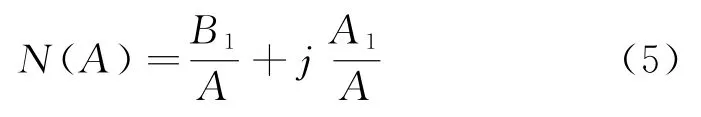
其中,A是描述函数的变量,满足:
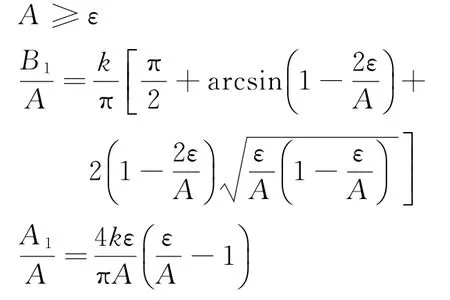
将图1所示的滚动通道控制系统结构图改写成如图2所示的非线性控制系统方框图。
则图中的滚动通道开环传递函数为

则根据描述函数理论,非线性系统产生极限环的振荡条件为
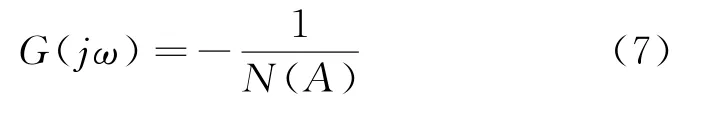
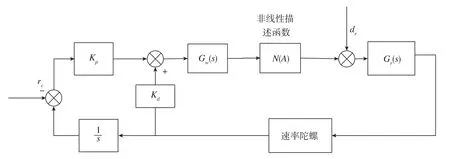
图2 描述函数法中滚动通道控制系统结构图Fig.2 Structure diagram of the roll channel control system in description function method
选定某一组控制参数得到如图3所示的某型号舵机的间隙特性描述函数-1/N(A)(黑色圈线)与滚动通道的开环Nichols图 (蓝色实线)。
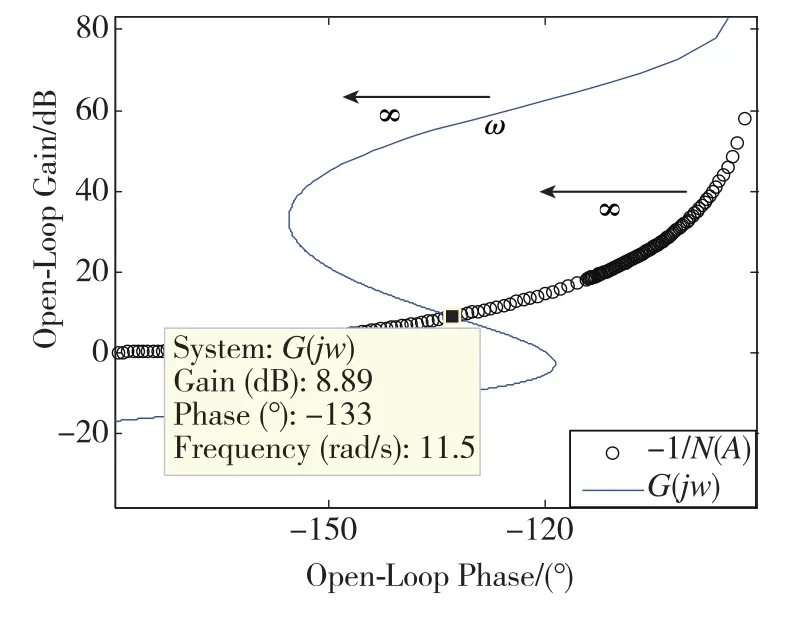
图3 G(jω)和-1/N(A)曲线的Nichols图Fig.3 Nichols graph of G(jω)and-1/N(A)
图3中,2个ω曲线在11.5rad/s处有一个交点,通过分析可知这是一个自持振荡点,对应的ε/A约为0.71,即自持振荡频率为11.5rad/s,幅值为ε/0.71,文中间隙宽度取0.3,即ε=0.15。
3 滚动通道极限环振荡研究
由第2节可以得到以下结论:1)自持振荡的存在与否取决于开环线性部分传递函数G(jω)与非线性描述函数曲线-1/N(A)是否有交点;2)假如有交点,交点决定了自持振荡的幅值和频率,由于间隙特性已经确定,则交点的位置由线性部分G(jω)决定。所以这一节将探讨G(jω)中的各项变量对自持振荡的影响。考虑到交点一般在低频段,舵系统线性部分Gw(jω)的剪切频率较高,对交点位置影响不大,所以本文从弹体特性Gr(jω)和控制参数Gc(jω)去讨论。
由此得到开环传函线性部分为
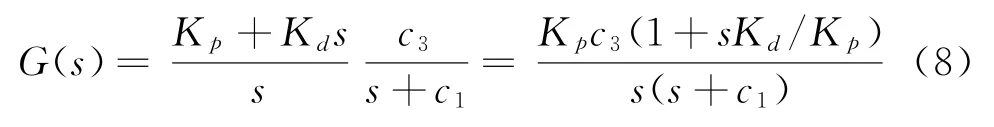
式中,可知G(jω)的频率特性由c1、Kpc3和Kd/Kp3部分决定。其中,c1是弹体的自然阻尼,Kpc3决定控制系统的快速性,Kd/Kp决定控制系统的阻尼特性。下面分别从3个方面进行研究分析。
3.1 控制系统快速性
针对相同的滚动通道动力系数,根据快速性指标要求设计不同的控制参数如表1所示。
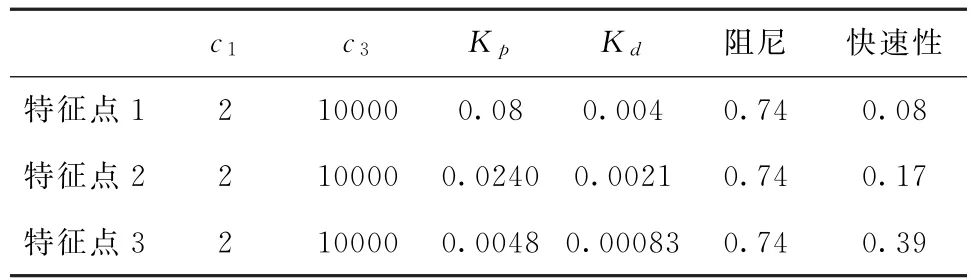
表1 不同快速性下控制参数列表Tab.1 List of control parameters under different rapidity
表1中,3个特征点的Nichols图如图4所示,图5所示为不同特征点的1°等效副翼干扰舵系统响应曲线。
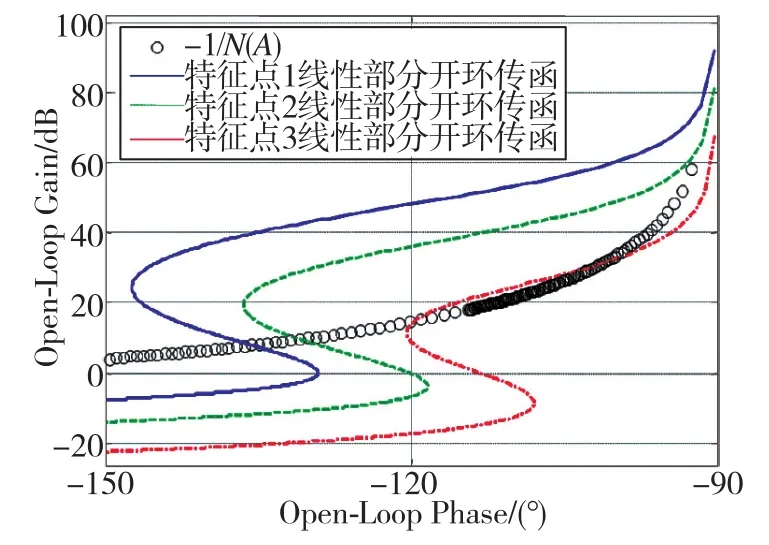
图4 特征点1~特征点3线性部分的Nichols图Fig.4 Nichols graph of the linear part of the control system at feature points 1~feature points 3
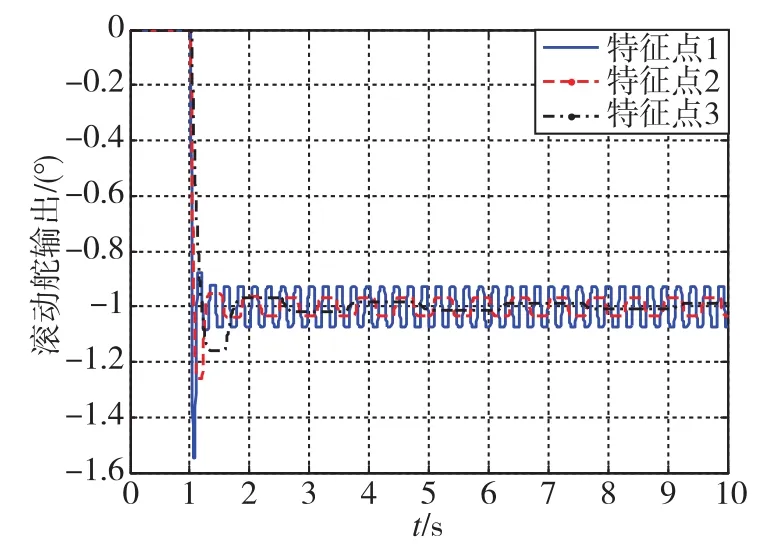
图5 特征点1~特征点3 1°等效副翼干扰下的舵偏响应曲线Fig.5 Response of rudder under 1°equivalent rudder interference at feature points 1~feature points 3
根据图4与图5,对极限环振荡的性能进行总结得到表2。
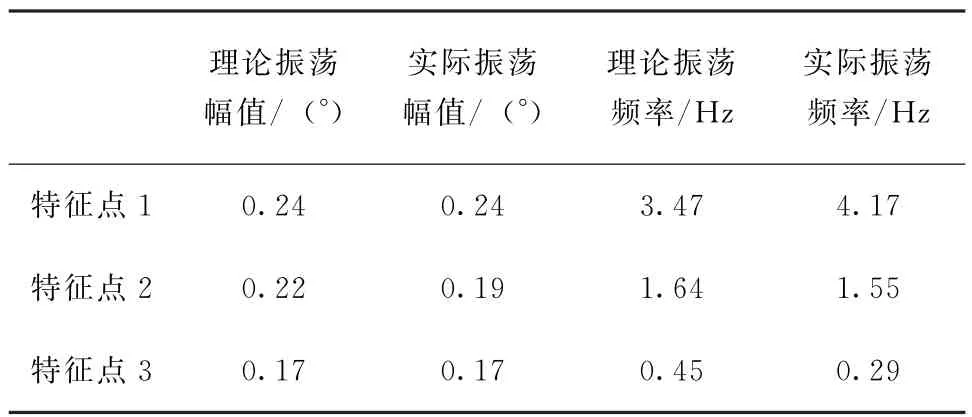
表2 不同快速性特征点极限环振荡性能总结Tab.2 Summary of limit cycle oscillation performance of different rapidity characteristic points
根据图4~图5、表1~表2可知,系统快速性设计得越慢,间隙带来的极限环振荡频率越低。
3.2 控制系统阻尼
针对相同的动力系数设计不同的控制参数使之有不同的阻尼特性,如表3所示。
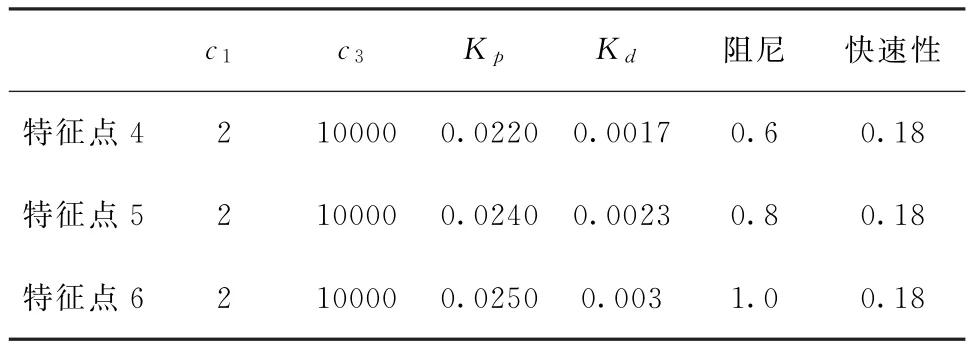
表3 不同快速性下控制参数列表Tab.3 List of control parameters under different rapidity
表3中,3个特征点的Nichols图如图6所示,图7所示为不同特征点的1°等效副翼干扰舵系统响应曲线。
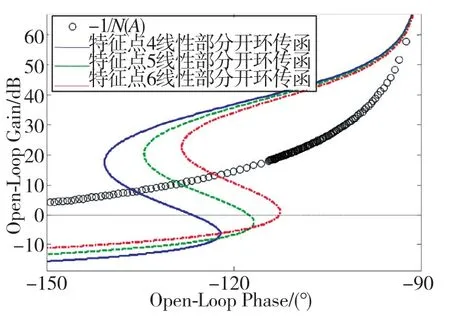
图6 特征点4~特征点6线性部分的的Nichols图Fig.6 Nichols graphs of the linear part of the control system at feature points 4~feature points 6
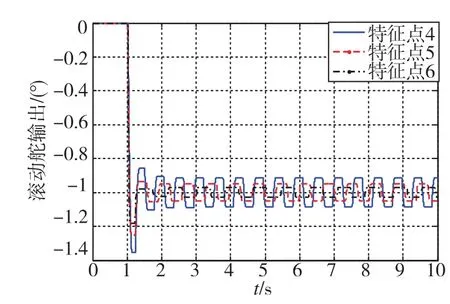
图7 特征点4~特征点6在1°等效副翼干扰下的舵偏响应曲线Fig.7 Response of rudder under 1°equivalent rudder interference at feature points 4~feature points 6
根据图6与图7对极限环振荡的性能进行总结得到表4。
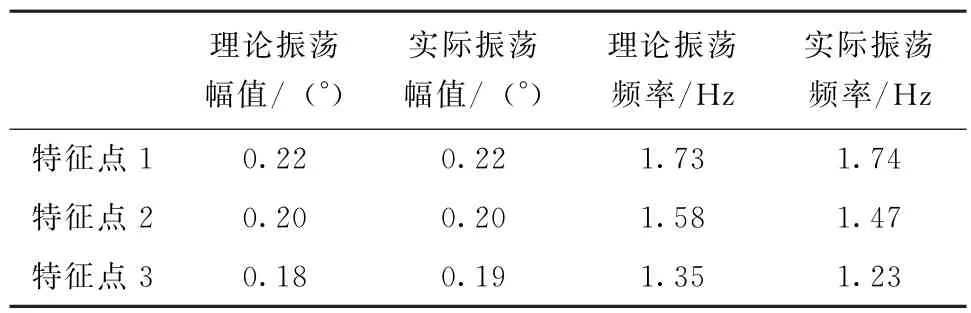
表4 不同快速性特征点极限环振荡性能总结Tab.4 Summary of limit cycle oscillation performance of different rapidity characteristic points
根据图6~图7、表3~表4可知,控制系统阻尼设计的大小对间隙带来的极限环振荡特性影响不大。
3.3 飞行器固有阻尼
针对不同飞行器固有阻尼c1的特征点,设计相同的快速性和阻尼,得到如表5所示的不同特征点的控制参数。
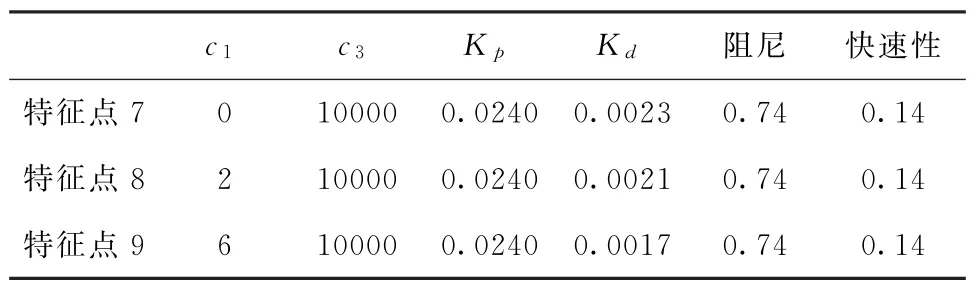
表5 不同固有阻尼下控制参数列表Tab.5 List of control parameters under different inherent damping
表5中,3个特征点的Nichols图如图8所示,图9所示为不同特征点的1°等效副翼干扰舵系统响应曲线。

图8 特征点7~特征点9控制系统线性部分的Nichols图Fig.8 Nichols graph of the linear part of the control system at feature points 7~feature points 9
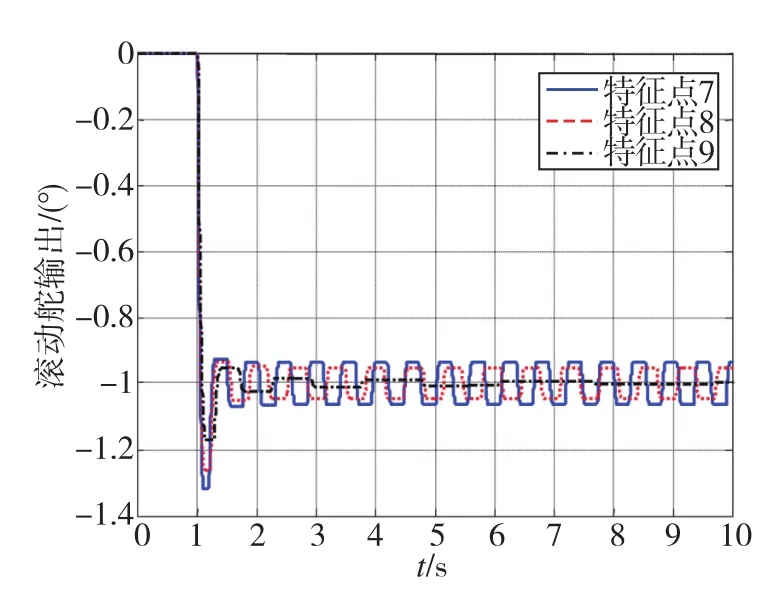
图9 特征点7~特征点9在1°等效副翼干扰下的舵偏响应曲线Fig.9 Response of rudder under 1°equivalent rudder interference at feature points 7~feature points 9
根据图8与图9对极限环振荡的性能进行对比得到表6。
根据图8~图9、表5~表6可知,弹体的固有阻尼c1的大小对间隙带来的极限环振荡影响较大,当c1达到一定值时,舵系统间隙非线性将不会产生极限环振荡现象。
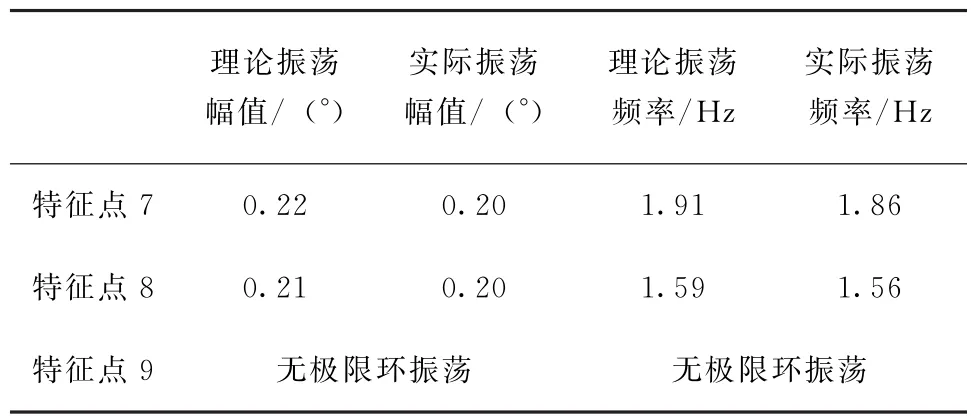
表6 不同固有阻尼的特征点极限环振荡性能对比Tab.6 Comparison of characteristic point limit cycle oscillation performance with different inherent damping
3.4 结果对比分析
3.1~3.3节以滚动通道为分析对象,通过对比仿真结果可知,从飞行控制系统方面来看,控制系统的阻尼对极限环振荡的幅值和频率影响较小;控制系统的快速性对极限环振荡的频率影响较大,快速性越慢,振荡频率越低;滚动通道的自然阻尼c1大小对极限环振荡的影响较大,c1越大,振荡幅值和频率均越低,当c1大于某一值时,极限环振荡消失。这说明当舵系统存在非线性特性影响控制系统性能、且快速性指标较为严苛时,可通过在飞行器设计过程中增大滚动通道固有阻尼特性,降低舵系统非线性特性对控制系统的影响。
4 结 论
针对舵系统的非线性特性使得飞控系统产生稳态误差和极限环振荡等不良特性,本文从飞行控制系统的层面出发,以飞控系统滚动通道为研究对象,应用描述函数法,分别从控制系统快速性、阻尼、飞行器固有阻尼对极限环振荡特性的影响进行分析仿真对比。仿真结果表明,增大滚动通道的固有阻尼能有效降低舵系统非线性对控制系统性能的影响,甚至可以消除极限环振荡现象。此结论可有效指导飞行器外形设计,特别是当飞行器舵效率过高、控制精度较低导致舵系统非线性带来的极限环振荡对稳定控制系统性能影响较大时,具有较大的工程应用价值。

