基于Copula函数的多变量水文不确定性处理器
刘章君,郭生练,何绍坤,巴欢欢,尹家波
(1.武汉大学 水资源与水电工程科学国家重点实验室,水资源安全保障湖北省协同创新中心,湖北 武汉 430072;2.江西省水利科学研究院,江西 南昌 330029)
1 研究背景
水文不确定性处理器(Hydrologic Uncertainty Processor,HUP)作为贝叶斯预报系统(Bayesian Forecasting System,BFS)[1]的一个重要组件,用来量化除定量降水预报不确定性以外的其他所有不确定性,在实际中应用广泛[2-5]。然而,HUP属于单变量结构类型,只能独立地给出各预见期实际流量的贝叶斯后验概率密度,而没有考虑它们之间的内在相关性。Krzysztofowicz和Maranzano[6]以单步马尔科夫转移密度函数为工具,提出了基于贝叶斯转移预报(Bayesian Transition Forecast,BTF)方法的多变量水文不确定性处理器(Multivariate HUP,MHUP),可以在给定确定性预报过程的条件下提供实际流量过程的后验联合概率密度函数,考虑了不同预见期流量之间的相关性。在此基础上,针对传统的贝叶斯概率洪水预报方法均只能提供某一时刻流量的概率预报,无法满足决策者对某一时段内最大流量的预报不确定性信息的实际需求[7-8],Krzysztofowicz定义了极值概率预报的概念,并利用MHUP输出产品给出了极值变量的超越概率分布函数,提出了贝叶斯极值预报(Bayesian Extremum Forecast,BEF)方法[9]。
BTF方法是MHUP的基本组成构件,通常采用基于正态分位数转换和线性-正态假设的亚高斯模型进行计算,但这种正态分位数转换在外推极端事件时效果不稳健,且逆转换时也可能使结果偏离最优值,影响了该法的适用性[10-11]。鉴于Copula函数能较好地模拟水文过程的非线性和非正态特征,在构建多变量联合分布和条件分布中具有巨大优势[12-15],刘章君等[11]提出了基于Copula函数的HUP(CHUP),不需要进行线性-正态假设,适用范围更广,应用更加灵活。事实上,BTF方法中的先验转移密度和似然函数本质上也都是条件概率密度函数,但目前没有文献将Copula函数引入BTF方法、MHUP及BEF方法的研究中。
因此,本文将采用Copula函数描述BTF方法中的先验转移密度和似然函数,推导后验转移密度的解析表达式,提出基于Copula函数的贝叶斯转移预报(CBTF)方法,得到基于Copula函数的多变量水文不确定性处理器(CMHUP),进而利用CMHUP输出的各预见期实际流量后验联合概率密度函数,导出预见期时段内洪峰流量的超过概率分布函数,发展基于Copula函数的贝叶斯极值预报(CBEF)方法。以三峡水库为例进行应用,基于所提方法实现三峡水库入库流量的转移概率预报和极值概率预报。
2 多变量水文不确定性处理器
假设H0表示预报时刻的当前实测流量,分别表示待预报的实际流量和确定性预报流量,K为预见期长度;h0、hk和sk分别为随机变量H0、Hk和Sk的实现值。多变量水文不确定性处理器的目的是在给定当前实测流量H0=h0、确定性预报过程随机向量的实现值的条件下,推求得到实际流量过程随机向量的后验联合概率密度函数。利用概率乘法定理,后验联合概率密度函数可以因式分解为[6]:
相应地,式(1)也可以简化为:

3 基于Copula函数的贝叶斯转移预报方法
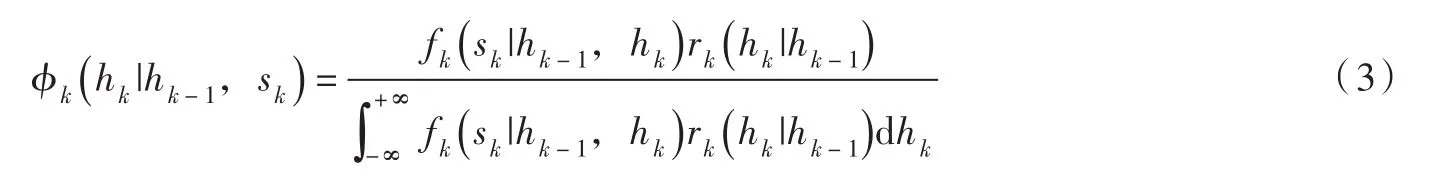
3.1Copula函数Copula函数可以将多个随机变量的边缘分布连接起来构造联合分布。令G(x1,x2,…,xn)为一个n-维分布函数,其边缘分布分别为则存在一个n-Copula函数C,使得对任意x∈Rn(x为n维向量,Rn为n维实数空间)[13]:
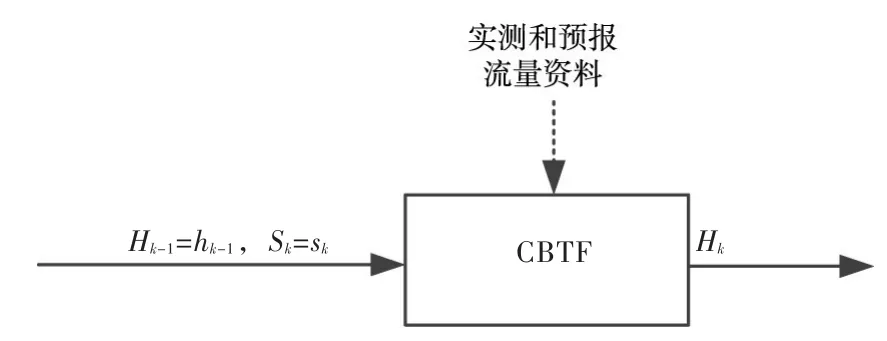
图1 CBTF方法概念示意图

式中:θ为Copula函数的相关性参数。
Copula函数可以将多个变量的边缘分布和它们之间的相关性结构分开来研究,且对边缘分布类型没有任何限制。采用Copula函数进行多变量建模时,通常包括两个步骤:①确定各个变量的边缘分布;②选择合适的Copula函数,描述变量之间的相关性结构。
本文选用Archimedean Copula函数族构造联合分布,采用K-S检验法对Copula函数进行拟合检验的基础上,基于RMSE准则评价联合分布的理论频率与经验频率拟合情况,选择RMSE值最小的Copula函数作为最优的Copula函数,其数学表达式、参数估计方法、K-S检验法及RMSE值等,详见文献[12-15]。
3.2先验分布考虑到变量Hk-1和Hk具有相同的边缘分布,在表示概率分布函数和密度函数时统一为随机变量H。利用Copula函数,Hk-1、Hk的联合分布可写为:

先验转移概率分布为给定Hk-1=hk-1时,Hk的条件分布函数为[18-19]:
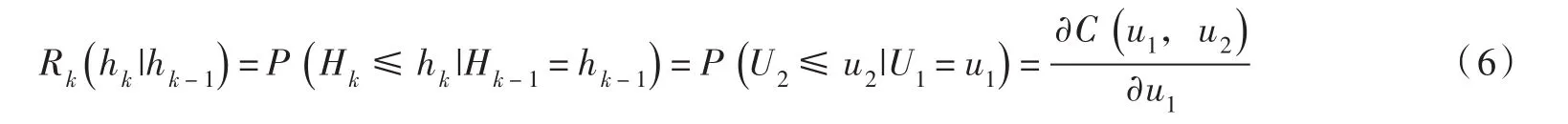
先验转移密度函数:

3.3似然函数令Sk的边缘分布函数为相应的概率密度函数为借助Copula函数,Hk-1、Hk和Sk的联合分布可写为:
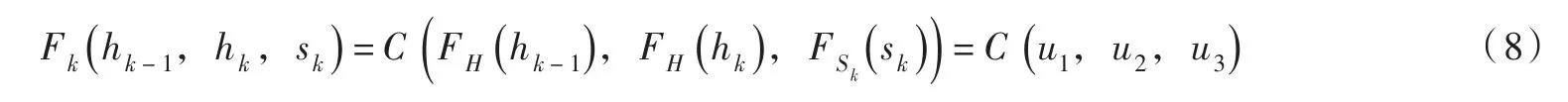
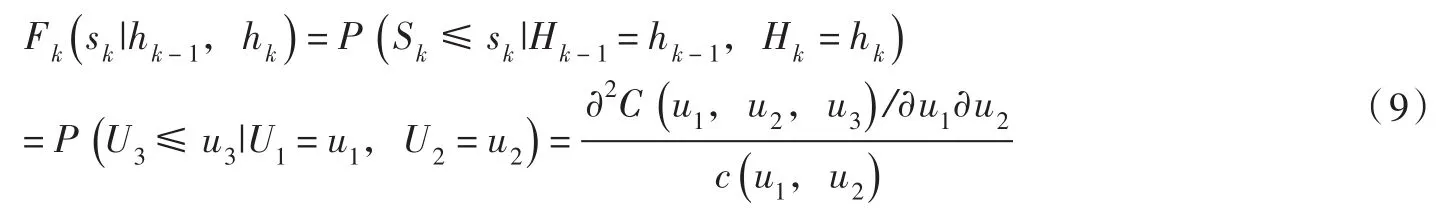
相应的密度函数:
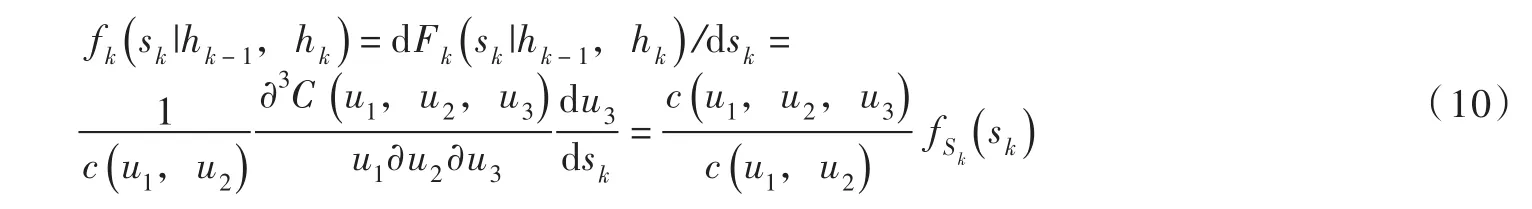
3.4后验分布将式(7)和式(10)代入式(3),可以推导得到实际流量Hk后验转移密度函数的解析表达式:

相应的后验转移分布函数为

根据数理统计原理,可以计算得到期望值作为确定性预报结果,同时获取给定置信水平下的流量预报区间。实测流量的期望值hke通过下式求解:

令实测流量Hk取值出现在分布两端的概率为ξ,就可以定义Hk的置信水平为(1-ξ)的区间估计。实测流量Hk置信区间的两个端点分别由以下两式给出[22]:
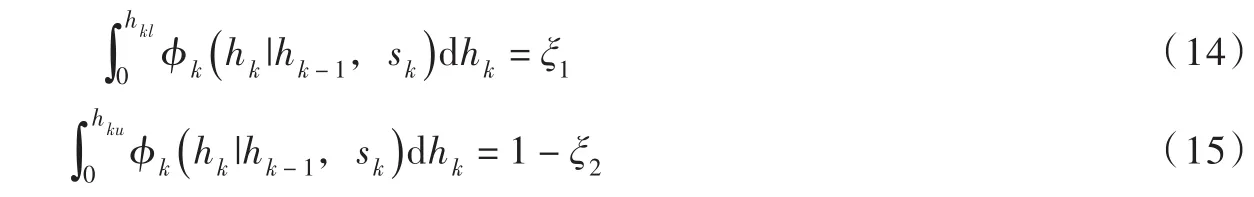
因此有

即[hkl,hku]为实测流量Hk置信水平(1-ξ)的区间估计,根据置信区间可以对Hk的转移预报不确定性进行定量评价。
4 基于Copula函数的贝叶斯极值预报方法
4.1极值概率预报的定义令随机变量Zk代表时段(0,k]的最大实际流量,这个新定义的一维连续随机变量可以看成是随机变量的极大值变量,它由一个时间离散的流量随机过程{H1,…,Hk}衍生而得。

对于任意给定的流量值h,设为最大实际流量Zk的超过概率分布函数,通过下式定义:

将式(17)代入,并进行演算可得:
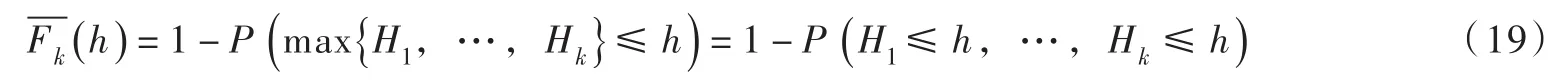
4.2CBEF方法的数学描述CBEF方法的概念流程示意图如图2所示。从式(19)可以看出,对于任意给定的流量值h,求解超过概率分布函数的关键在于计算得到联合概率分布值


图2 CBEF方法概念示意图

则式(19)可以重新写为:

5 实例应用
三峡工程是开发与治理长江的关键性骨干工程,具有防洪、发电、航运、补水等综合效益。三峡水库集水面积约为100万km2,坝址多年平均流量为14 300 m3/s。本文基于CBTF方法实现三峡水库汛期入库流量的转移概率预报,进而基于CBEF方法实现三峡水库汛期入库流量的极值概率预报。选用2003—2016年汛期(6月1日—9月30日)发生的22场实测入库洪水过程及长江水文气象预报中心发布的预见期1~3 d相应的确定性预报入库洪水过程资料。实测值和预报值均为每日8时入库流量,取样时以预见期对应的洪水发生的实际时间为基础,反推相应的预报发布时刻,同步样本数均为707次。
5.1边缘分布的确定边缘分布函数可以采用任意分布,选用的标准是使得假定理论分布与流量资料拟合较好。本文采用P-Ⅲ分布作为实际流量和预报流量的边缘分布,其密度函数表达式如下[23]:
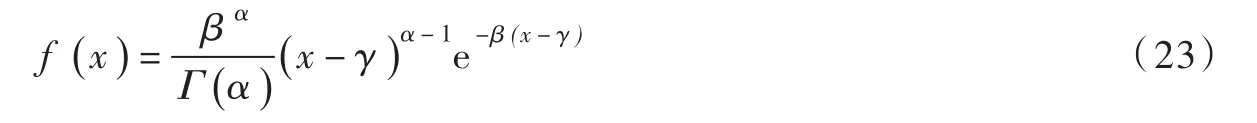
式中:α、β和γ分别为形状、尺度和位置参数。
考虑到变量Hk(k=1,2,3)的边缘概率分布相同,将其统一表示为随机变量H。采用P-Ⅲ分布线型分别作为H、Sk(k=1,2,3)的理论线型,利用L-矩法估计参数,结果见表1。采用K-S检验法分别对4个随机变量进行拟合检验,单变量K-S检验统计量D值也列于表1。结果表明,在5%的显著性水平下,K-S检验统计量D均小于相应的临界值(0.0511),各变量均通过了检验。因此,估计的实际流量和预报流量边缘分布是合理可行的。
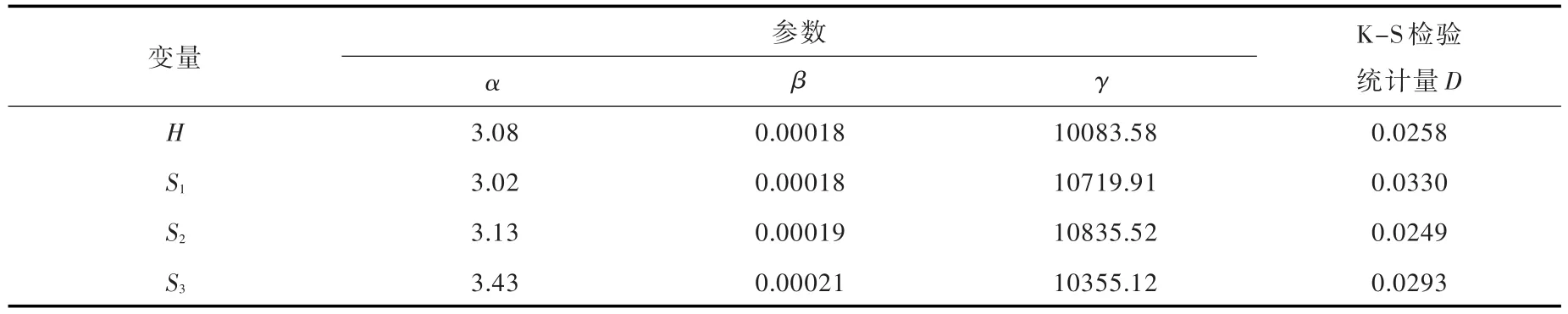
表1 边缘分布参数估计结果和K-S检验
5.2联合分布的建立变量两两之间的Kendall秩相关系数矩阵见表2。可以发现,3个变量之间的相关性是不对称的,Hk和Sk的相关性最高,且Hk-1和Hk、Hk-1和Sk的相关性基本相当。
考虑到Hk-1、Hk的联合分布与H0、H1的联合分布相同,因而只需要估计H0、H1的联合分布。分别采用二维Gumbel-Hougaard、Clayton和Frank Copula函数分别构造H0、H1的联合分布,基于不同预见期的同步系列数据,分别得到相应的Kendall秩相关系数τ,根据τ与参数θ的关系分别计算Copula函数的参数值,结果见表3。二维K-S检验统计量D和RMSE值也列于表3。可知,在5%的显著性水平下,3种备选Copula函数的二维K-S检验统计量D均小于临界值(0.0511),并且二维Frank Copula函数的RMSE值均为最小,因而选择其构造H0、H1的联合分布。
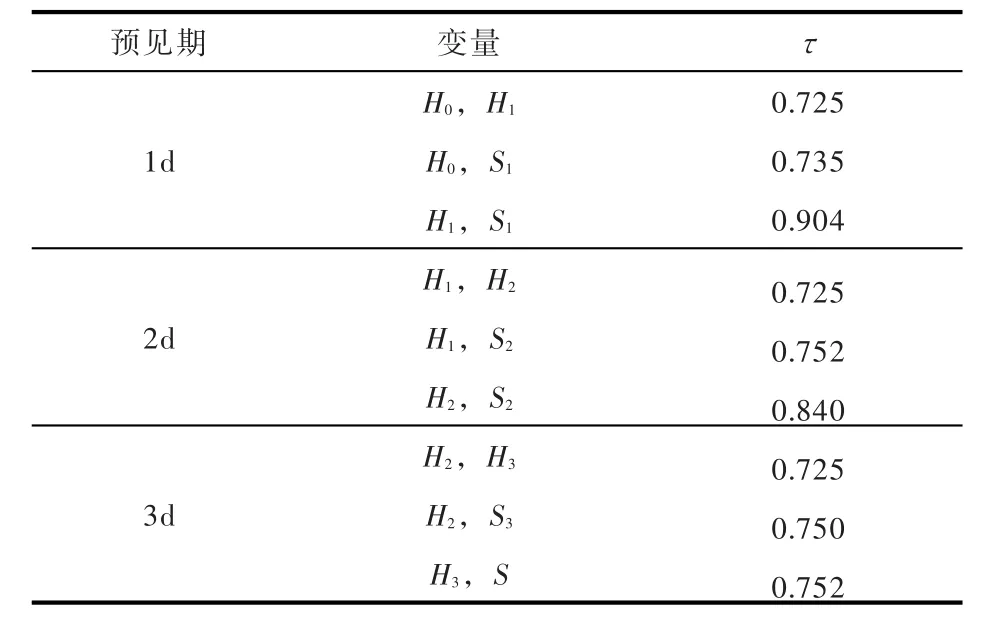
表2 变量Hk-1,Hk和Sk两两之间的Kendall秩相关系数矩阵

表3 H0和H1联合分布参数估计、检验及优选结果
分别采用三维非对称Gumbel-Hougaard、Clayton和Frank Copula函数分别构造Hk-1,Hk和Sk的联合分布,基于不同预见期的同步系列数据,利用极大似然法估计的三维非对称Copula函数参数值、三维K-S检验统计量D和RMSE值列于表4。可以发现,在5%的显著性水平下,对于预见期1 d和2 d三维非对称Gumbel-Hougaard Copula函数和Frank Copula函数通过了K-S检验(临界值0.0511),而预见期3 d只有三维非对称Frank Copula函数通过了检验。而且,3个预见期三维非对称Frank Copula函数均给出了最小的RMSE值,因此选择其构造Hk-1,Hk和Sk的联合分布。

表4 Hk-1、Hk和Sk三维非对称Copula函数参数估计、检验及优选结果
5.3转移概率预报结果示例任意给定实际流量Hk-1和确定性预报流量Sk(k=1,2,3)的取值,就可以求解实际流量Hk的后验转移概率密度和后验转移分布函数,实现入库流量的转移概率预报。在实际分析Hk的后验不确定性时,实际流量Hk-1的取值是未知的,其取值状态可以是可行域中的任何值。以预报时刻2003年7月5日(20030705)为例,预报时刻的实测流量h0=33 700 m3/s。图3和图4分别给出了h0(为已知值)、h1和h2取各种不同状态时,预见期1~3 d实际入库流量Hk的后验转移密度函数曲线和后验转移分布函数曲线。可知,后验转移分布呈现正偏态特征,CBTF方法可以准确地描述相邻两个预见期流量之间的后验转移概率密度和分布函数,从而定量评估转移预报的不确定性。
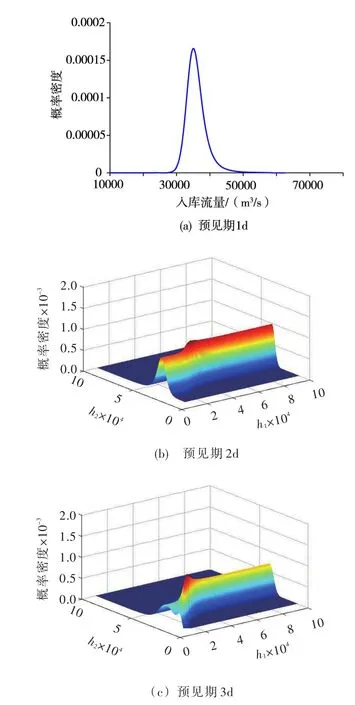
图3 三峡水库20030705入库流量后验转移密度曲线
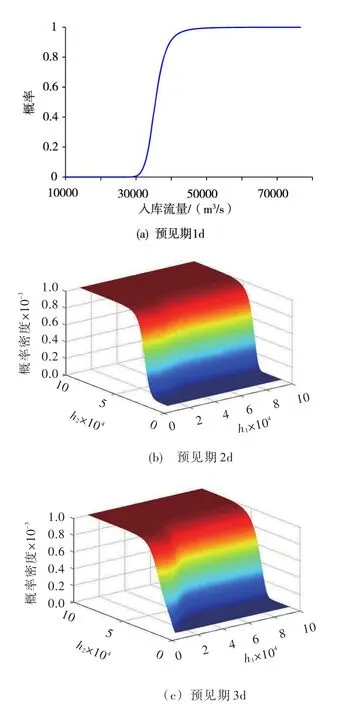
图4 三峡水库20030705入库流量后验转移分布曲线
为了展示入库流量预报不确定性在时间上的演变特征,我们把实际发生的流量过程当作已知值(h0=33 700 m3/s,h1=36 100 m3/s,h2=38 600 m3/s和h3=43 000 m3/s),对应的确定性预报结果过程为(s1=35 500 m3/s,s2=38 000 m3/s和s3=37 500 m3/s)。三峡水库20030705入库流量预报先验和后验不确定性随时间的演变过程见图5,其中红色实点代表实际值,虚线为实际流量过程。可以发现,随着预见期的延长或者时间的推移,入库流量预报的先验和后验转移密度函数由陡变缓,表明预报不确定性增大,这与实际情况相符。但利用确定性预报信息经过贝叶斯修正之后的后验转移密度函数与相应的先验密度函数相比都更加尖瘦和集中,不确定性更小。CBTF方法和CMHUP为分析水文预报不确定性在时间上的演变特征提供了有效工具。
图6给出了三峡水库“20160701”号洪水过程预见期1~3 d的后验期望值和90%置信区间及实际值。可以看出,洪水流量的量级越大,相应的不确定性一般也越大。后验期望值预报与实际流量序列拟合效果总体较好,但拟合效果随预见期的延长而降低。此外,90%预报区间也随着预见期的延长均变宽,预报不确定性增大,但基本上可以包住实际流量,表明概率区间预报是可靠的,可以为水库防洪调度决策提供更多的风险信息。
5.4转移概率预报结果评价基于整个研究数据集(样本数为707),从后验期望值预报的精度和概率预报的整体性能对CMHUP的转移概率预报结果进行评价,并与CHUP的结果进行对比分析。从理论定义上讲,CHUP描述的是k步流量状态转移H0→Hk(k=1,2,3)的不确定性,而CMHUP描述的则是单步流量状态转移Hk-1→Hk的不确定性。需要指出的是,预见期1 d时两者结果是相同的,描述的都是状态转移H0→H1的不确定性,以下重点分析预见期2 d、3 d的情形。
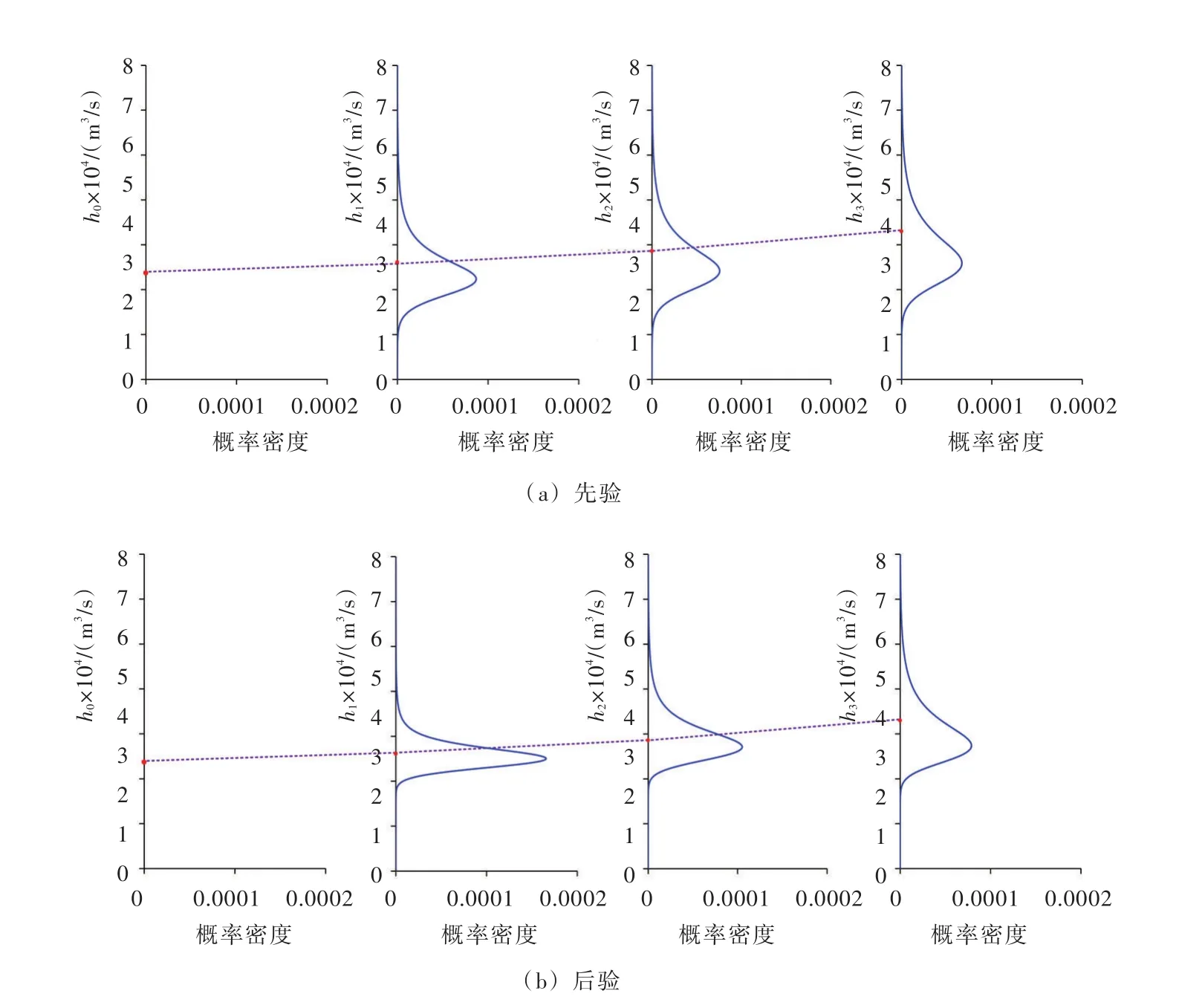
图5 三峡水库20030705入库流量预报不确定性随时间的演变过程
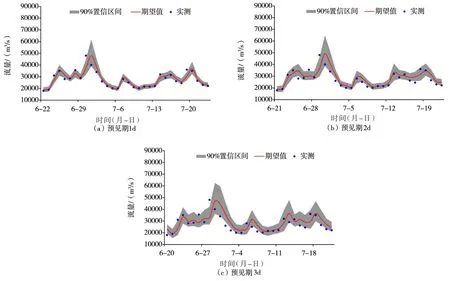
图6 三峡水库“20160701”号入库洪水流量实测值、期望值与90%置信区间
(1)后验期望值预报。三峡水库预见期1~3 d的确定性预报与CHUP、CMHUP后验期望值预报结果的精度评价指标R2和RE分别见表5。可以看出,相比确定性预报,CHUP、CMHUP后验期望值预报结果R2均有一定程度的提高,RE显著地减小,而且CMHUP的后验期望值预报相比CHUP略有改善。由于三峡水库的防洪库容较大,水库运行调度主要受洪水总量控制,因而准确地预报径流总量具有重要意义,相比于确定性预报而言,CHUP、CMHUP后验期望值预报在这方面显示出了很大优势。还可以发现随着预见期的延长,由于确定性预报精度的下降,导致CHUP、CMHUP后验均值预报的精度都相应地降低。

表5 不同预见期的确定性预报与CHUP、CMHUP后验期望值预报结果比较(单位:%)
(2)概率预报。采用可靠性(α-index)、分辨率(π-index)和连续概率排位分数(CRPS,确定性预报退化为平均绝对误差MAE)等指标来评定概率预报的整体性能[24-25]。CHUP、CMHUP不同预见期的α-index、π-index和CRPS等指标值列于表6。可知,不同预见期的α-index值均大于0.9,表明概率预报结果可靠性高。此外,随着预见期的延长,π-index值逐渐减小,概率预报的分辨率和精度降低,说明入库流量的预报不确定性增加。

表6 不同预见期的CHUP、CMHUP概率预报评价指标值比较
随着预见期的延长,CHUP、CMHUP计算的综合指标CRPS值也呈现不断增加的趋势,意味着概率预报的性能和总体效果降低。然而,基于CHUP、CMHUP得到的概率预报CRPS值,始终小于相应的确定性预报,彰显了概率预报的有效性。而且,CMHUP相比于CHUP也有不同程度的改善,表明入库流量单步状态转移的不确定性要低于多步转移。CMHUP计算的预见期1~3 d的CRPS值相比于确定性预报分别降低11.58%、18.52%和23.33%。
5.5最大入库流量超过概率分布函数根据样本空间同时考虑入库流量概率分布的特点,取累积概率超过0.9999的流量分位数值作为hk取值的上限hkmax=100 000 m3/s。因此,本文hk(k=1,2,3)的取值区间为10 100~100 000 m3/s,离散间距为100 m3/s,相应的离散点据数为900。以预报时刻2003年7月5日(20030705)为例,对于给定的流量值h(离散取值和hk相同),根据计算的转移概率预报结果,可以计算得到不同预见期内最大入库流量的超过概率分布函数超过概率分布曲线见图7。

图7 三峡水库20030705不同预见期内最大入库流量超过概率分布曲线
从图中可以读取不同预见期和给定流量值h对应的最大入库流量超过概率,例如1 d内最大入库流量超过35 000 m3/s的概率,2 d内最大入库流量超过40 000 m3/s的概率3 d内最大入库流量超过50 000 m3/s的概率另外,还可以计算得到3 d内最大入库流量对应的90%置信区间为[35100,56700]m3/s,提供了预见期时段内最大入库流量预报的不确定性和风险信息。
6 结论
本文提出了基于Copula函数的贝叶斯转移预报(CBTF)方法和基于Copula函数的多变量水文不确定性处理器(CMHUP),进而发展了基于Copula函数的贝叶斯极值预报(CBEF)方法。以三峡水库为例进行应用,主要研究结论如下:(1)CBTF方法不需要进行线性-正态假设,可以在原始流量数据空间给出贝叶斯后验转移密度函数的解析表达式,能够很好地捕捉流量过程的非线性和非正态特征,适用范围更加广泛。(2)CMHUP可以在给定当前实测流量和确定性预报过程的条件下,更加灵活地给出考虑实际流量过程内在相关性结构的后验联合概率密度函数,为分析水文预报不确定性在时间上的演变特征提供了有效工具。(3)CBEF方法给决策者提供了预见期时段内最大入库流量预报的不确定性和风险信息,对防洪预报预警和减灾具有重要的参考价值。
本文采用Copula函数取代原有基于正态分位数转换和线性-正态假设的亚高斯模型,不仅在理论上存在优势,而且实用有效。然而,本文方法在假定实际流量过程服从一阶马尔科夫过程的基础上推导得到,对于流量过程服从两阶及以上马尔科夫过程的情形本文方法的思路仍然适用,但需要采用更高维的Copula函数,计算更加复杂,有待进一步研究。另外,如何将定量降水预报不确定性与本文所提方法进行耦合,估计转移预报和极值预报的总不确定性,也需要进一步探讨。
参考文献:
[1]KRZYSZTOFOWICZ R.Bayesian theory of probabilistic forecasting via deterministic hydrologic model[J].Water Resources Research,1999,35(9):2739-2750.
[2]KRZYSZTOFOWICZ R,KELLY K S.Hydrologic uncertainty processor for probabilistic river stage forecasting[J].Water Resources Research,2000,36(11):3265-3277.
[3]李向阳,程春田,林剑艺.基于 BP神经网络的贝叶斯概率水文预报模型[J].水利学报,2006,37(3):354-359.
[4]鄢来标,康玲.河道洪水概率预报方法研究[J].水力发电,2008,34(12):40-41.
[5]蒋晓蕾,梁忠民,王春青,等 .BFS-HUP模型在潼关站洪水概率预报中的应用[J].人民黄河,2015,37(7):13-15.
[6]KRZYSZTOFOWICZ R,MARANZANO C J.Hydrologic uncertainty processor for probabilistic stage transition forecasting[J].Journal of Hydrology,2004,293(1):57-73.
[7 ]KRZYSZTOFOWICZ R.A theory of flood warning systems[J].Water Resources Research,1993,29(12):3981-3994.
[8]程晓陶,李娜,王艳艳,等 .防汛预警指标与等级划分的比较研究[J].中国防汛抗旱,2010,20(3):26-31.
[9 ]KRZYSZTOFOWICZ R.Probabilistic flood forecast:Exact and approximate predictive distributions[J].Journal of Hydrology,2014,517(1):643-651.
[10]MADADGAR S,MORADKHANI H.Improved Bayesian multimodeling:Integration of copulas and Bayesian model averaging[J].Water Resources Research,2014,50(12):9586-9603.
[11]刘章君,郭生练,李天元,等.贝叶斯概率洪水预报模型及其比较应用研究[J].水利学报,2014,45(9):1019-1028.
[12]SALVADORI G,de MICHELE C.On the use of copulas in hydrology:theory and practice[J].Journal of Hydrologic Engineering,2007,12(4):369-380.
[13]郭生练,闫宝伟,肖义,等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文,2008,28(3):1-7.
[14]孙鹏,张强,陈晓宏.基于Copula函数的鄱阳湖流域极值流量遭遇频率及灾害风险[J].湖泊科学,2011,23(2):183-190.
[15]冯平,李新 .基于Copula函数的非一致性洪水峰量联合分析[J].水利学报,2013,44(10):1137-1147.
[16]MARANZANO C J,KRZYSZTOFOWICZ R.Identification of likelihood and prior dependence structures for hydrologic uncertainty processor[J].Journal of Hydrology,2004,290(1-2):1-21.
[17]ENGELAND K,STEINSLAND I.Probabilistic postprocessing models for flow forecasts for a system of catchments and several lead times[J].Water Resources Research,2014,50(1):182-197.
[18]刘曾美,覃光华,陈子燊,等.感潮河段水位与上游洪水和河口潮位的关联性研究[J].水利学报,2013,44(11):1278-1285.
[19]陈璐,卢韦伟,周建中,等.水文预报不确定性对水库防洪调度的影响分析[J].水利学报,2016,47(1):77-84.
[20]侯芸芸,宋松柏,赵丽娜,等.基于Copula函数的三变量洪水频率研究[J].西北农林科技大学学报(自然科学版),2010,38(2):219-228.
[21]梁忠民,郭彦,胡义明,等.基于copula函数的三峡水库预泄对鄱阳湖防洪影响分析[J].水科学进展,2012,23(4):485-492.
[22]刘章君,郭生练,李天元,等 .设计洪水地区组成的区间估计方法研究[J].水利学报,2015,46(5):543-550.
[23]中华人民共和国水利部.水利水电工程设计洪水计算规范(SL44-2006)[S].北京:中国水利水电出版社,2006.
[24]THYER M,RENARD B,KAVETSKI D,et al.Critical evaluation of parameter consistency and predictive uncertainty in hydrological modeling:A case study using Bayesian total error analysis[J].Water Resources Research,2009,45(12):1211-1236.
[25]李明亮,杨大文,陈劲松 .基于采样贝叶斯方法的洪水概率预报研究[J].水力发电学报,2011,30(3):27-33.

