基于高维Gaussian Copula函数的区域农田灌溉需水分析
杜奕良 ,涂新军 ,杜晓霞 ,陈晓宏 ,林凯荣 ,吴海鸥
(1.中山大学 水资源与环境系, 广东 广州 510275;2.广东省华南地区水安全调控工程技术研究中心, 广东 广州 510275)
1 研究背景
农田灌溉需水常受到农作物类型、播种面积、土壤类型、耕作制度、灌溉水利用系数和气候等因素的影响[1],其中气候特别是降水属于随机过程的不确定性因素,而其他因素可归为确定性因素。因此在区域水资源规划的农田灌溉需水分析中,通常需要推求从枯到丰多个降水频率条件下的需水。当区域空间尺度较大时,农田灌溉需水需要考虑上述因素的空间差异[2],一般是在各分区农田灌溉需水的基础上进行空间叠加,其中如何得到给定区域降水频率的分区组合是个难点。也就是说,空间尺度较大的区域农田灌溉需水分析,既要符合全区降水统计特征,还要反映各分区降水的空间关系。
以往的处理方法采用典型年法,即选择与某一给定年降水量频率相近的典型年,对各分区年降水量进行同倍比缩放[3-4]。但是降水空间组合关系并非一成不变的,某一区域降水频率下对应多种分区组合,如何选择分区组合属于多变量统计模拟和设计问题。Copula作为多维随机变量的连接函数,因其既可以呈现每一个随机变量的分布特征,同时又能反映变量之间的相依性,近些年被广泛应用于水文多维联合分布模拟[5-7]。其中也包括水文变量的空间组合模拟,如不同水文区的降水或径流丰枯遭遇[8-12],而且当确定了水文多维联合分布和边缘分布的理论模型及参数后,可进一步根据同频法和最大权函数法推求变量组合[13],如雨潮遭遇分析[14]、推求洪水过程线[15]和洪水风险评估[16]等。
本文以广东省农田灌溉需水为例,基于高维Gaussian Copula函数构建广东省8个农业分区的降水联合分布模型。考虑各分区降水和灌溉定额的空间差异,采用典型年法、同频法和最大权函数法,得到给定全省降水频率的分区及全省农田灌溉需水,并比较3种计算方法的区域需水、分区降水频率及需水空间组合特征与差异,为空间尺度较大的区域农田灌溉需水分析提供新思路。
2 研究方法
2.1分区降水联合分布模拟空间尺度较大区域的分区降水存在空间差异,但也存在相似降水成因。而分区降水的年系列一般认为是随机的。因此,可引入适用于高维的Gaussian Copula函数模拟分区降水的联合分布[17-18]。设为d个随机变量,其边缘分布函数分别为FX1(x1),…,d维Gaussian Copula的分布函数C(u1,…,ud)和密度函数c(u1,…,ud)分别为:
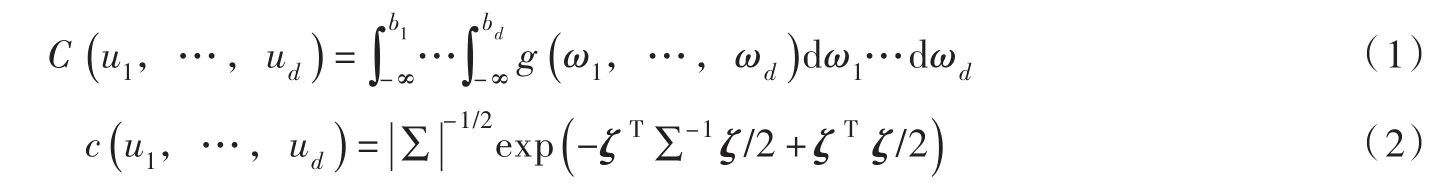
其中


式中:ρij∈[-1,1],i=1,…,d,j=1,…,d为任意两个变量之间的相关系数。
边缘分布模拟采用4种水文领域应用较为广泛的3参数单变量分布模型,即广义极值(Generalized Extreme Value,GEV)、广义 Logistic(Generalized Logistic,GLO)、皮尔逊Ⅲ型(Pearson Ⅲ,PE3)和广义正态(Generalized Normal,GNO)。拟合检验采用K-S方法,检验统计量D为[19]:
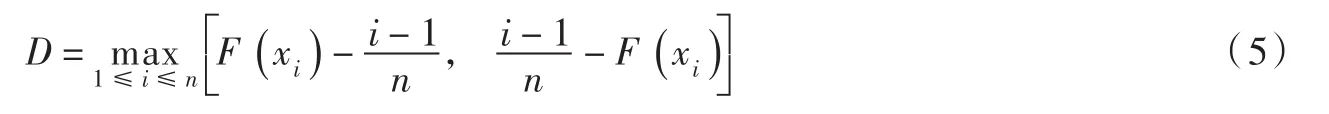
式中:n为样本长度。
多维联合分布拟合检验采用基于Rosenblatt变换的Cramervon Mises方法,检验统计量为[21]:

式中:E为基于Rosenblatt变换的伪随机变量,令E1=u1,则
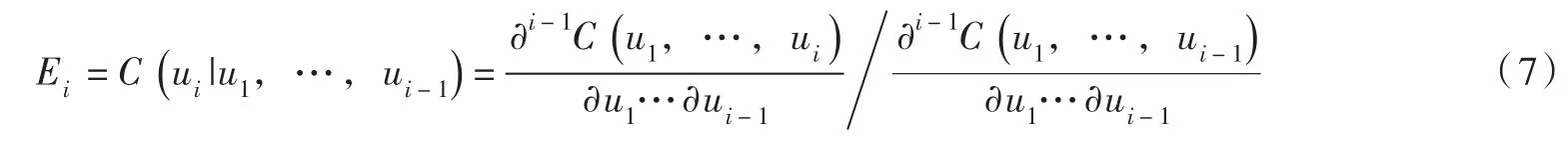
式中:i=2,…,d。
边缘和联合分布模型参数分别采用线性矩法[20]和极大似然法估计[21],再基于Monte Carlo方法模拟分别计算统计量D和的P值大小。若P>0.05,表明该模型在显著性检验水平为0.05情况下是可接受的。若有多个模型通过了统计检验,则根据均方根差RMSE和赤迟信息准则AIC进一步优选[21]。
2.2分区降水频率组合的推求方法区域降水频率是指分区降水经过面积加权平均后,拟合得到的理论分布函数。理论上给定一个区域降水频率,存在无数种分区降水频率组合。为此,可分别根据典型年法、同频法和最大权函数法推求分区降水频率组合。典型年法是指在实测样本中选择区域降水量较接近的年份,对降水空间组合进行同倍比缩放,进而得到分区降水频率组合的方法。同频法是指假定各分区降水频率相同情况下的区域降水空间组合方法。最大权函数法是在多维联合分布模拟基础上提出的[22-23],其定义为[13]:

具体分析步骤如下:
(1)根据样本确定的理论联合分布模型,采用Monte Carlo法模拟生成l组分区降水频率组合[u1(j),…,ui(j),…,ud(j)],j=1,…,l,计算分区降水量组合为[X1(j),…,Xi(j),…,Xd(j)],j=1,…,l及区域降水量X0(j),j=1,…,l与其降水频率u0(j),j=1,…,l。
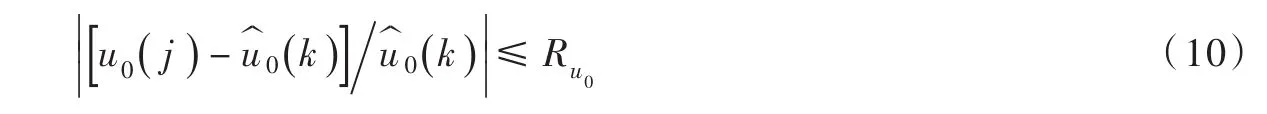
(4)考虑到Monte Carlo法生成分区降水频率组合的随机性,对于模拟优选的分区降水频率组合进一步给出置信区间。即重复分析步骤(1)—(3)B次,每个给定区域降水频率得到B组分区降水频率组合B和相应的联合分布概率密度则1-α置信区间的组合S()fα应满足:
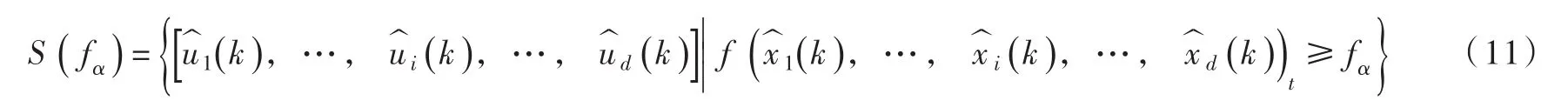
式中:fα为(1-α)分位数,
在B个组合中,联合概率密度值最大的组合即为最终的选择。
另外为了尽可能扩大模拟数和提高误差控制精度,本文研究l、Ru0、B和检验水平α分别取106、10-4、103和0.05。
2.3农田灌溉需水计算灌溉农业受气候、土壤、植被等自然条件的制约,土壤和植被等条件是相对稳定的,但降水却时刻在变化,是个随机因素。因此,农田灌溉需水是与降水有关的随机过程。水资源规划中分析农田灌溉需水,通常是明确灌溉农田面积A和灌溉水利用系数η,并给出不同降水频率下单位面积的农田灌溉净定额q(u)。因此,降水频率u的农田灌溉需水W(u)计算公式为:

对于空间尺度较大的区域来说(如省级行政区),认为区域内不同分区(如水资源分区、行政分区或农业分区等)的降水和灌溉定额是有差异的。因此,整个区域降水频率u0的农田灌溉需水是各分区的农田灌溉需水之和。
3 实例研究
3.1区域概括与数据广东省位于中国大陆最南端,全省面积17.96万km2。全省属于热带、南亚热带季风气候区,雨量充沛,但时空分布不均,旱涝常见。自1970年代末中国改革开放以来,随着当地社会经济快速发展,区域用水量不断增加。至2015年,全省总用水量443.1亿m3,其中农业用水227.0亿m3,且80%以上的农业用水为农田灌溉用水。
依据气候条件、土壤类型、耕作制度及作物布局等,广东省分为8个农业分区,见图1。目前,广东省农田灌溉基本采用一年两熟的耕作制度。根据灌溉试验和历史资料[24],各农业分区农田灌溉净定额,其理论统计分布(P-Ⅲ分布)参数特征值如表1所示。广东省在实行最严格水资源管理制度时,要求2020年各地市农田灌溉水有效利用系数介于0.51~0.55,因此本文灌溉水有效利用系数采用全省均值0.511。各分区农田灌溉面积则参照广东省水资源规划的2020年水田有效灌溉面积目标(见表1)。年降水量采用1953—2013年国家地面气候站点的逐日降水量过程,其中广东省内共25个水文站点,基于站点算术平均法得出各分区年降水量系列,其基本特征如表2。
全省年降水均值约为1819 mm。其中,高值区为分区V,均值为2789 mm,低值区为分区Ⅷ和Ⅲ,均值不足1600 mm;其他分区均值介于1600~2000 mm之间。分区最大年降水可达4071 mm(V,1973年)最小年份不足800 mm(Ⅵ,1963年;Ⅷ,1955)。各分区年降水变差系数介于0.146~0.221,全省则为0.153。
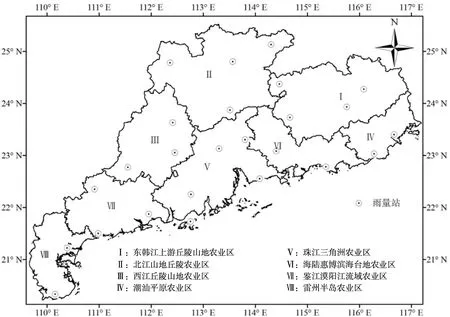
图1 广东省雨量站点分布及农业区区划图
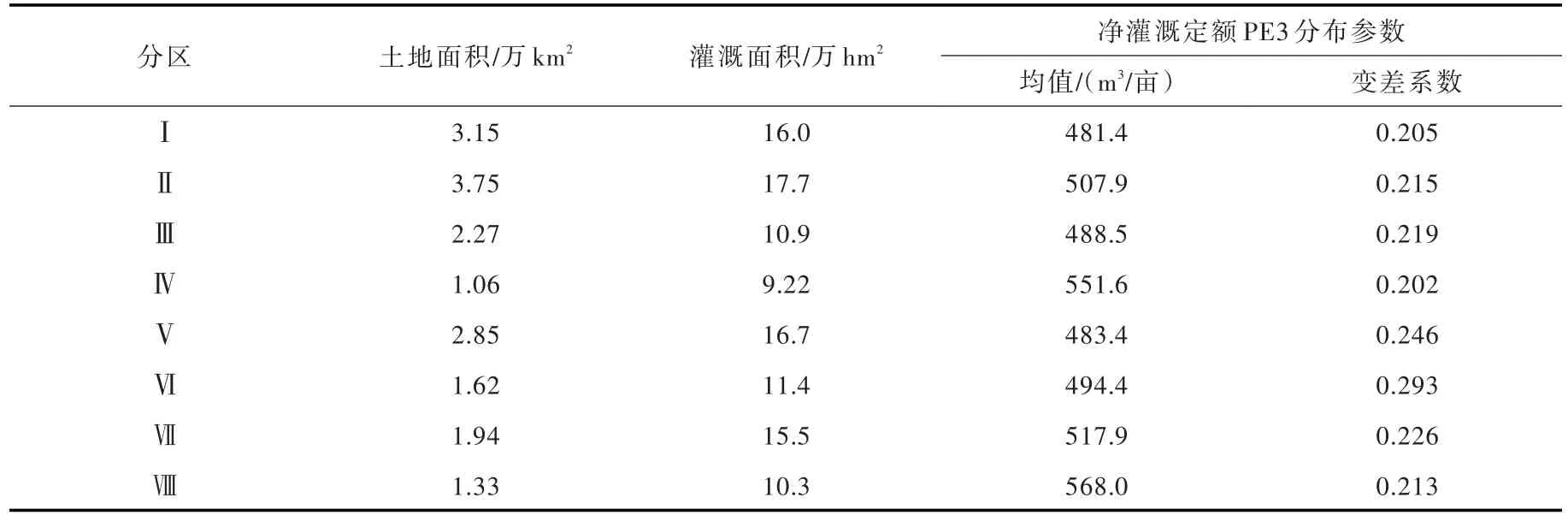
表1 分区土地面积、灌溉面积及净灌溉定额参数
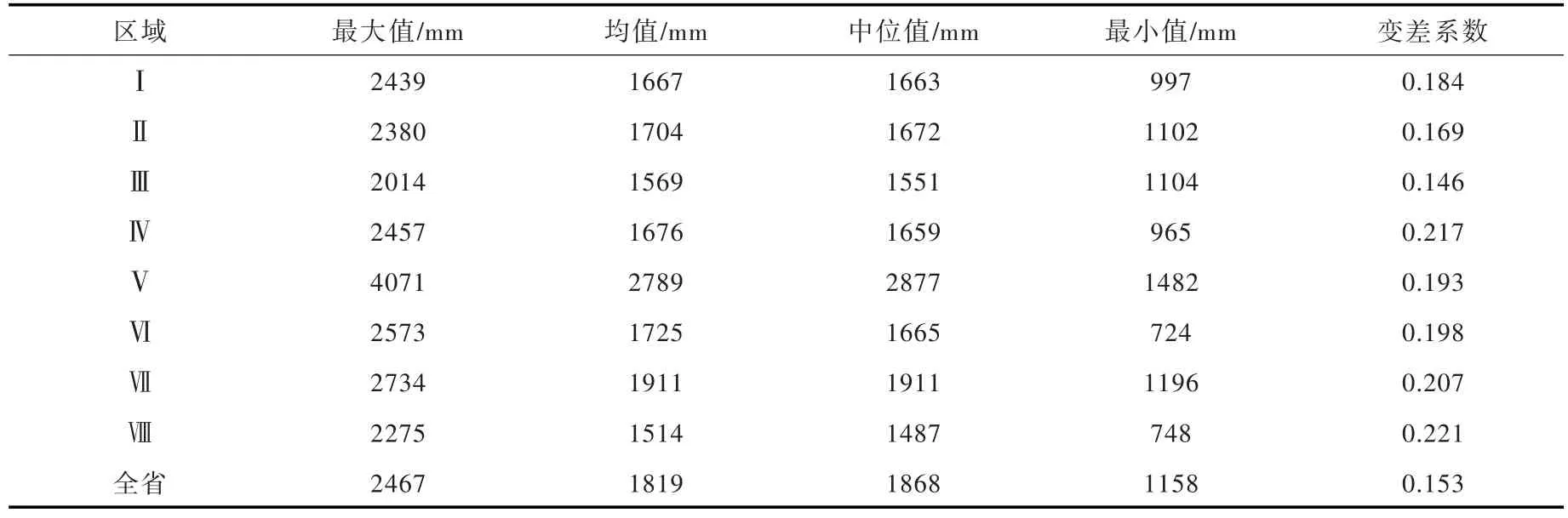
表2 年降水量基本特征
3.2降水分布特征分区及全省降水分布拟合检验结果如表3。所有单变量模型拟合P值均大于显著性检验水平0.05,表明均可作为年降水分布的备选模型。从RMSE和AIC值来看,模型之间差别非常小。基于最小值准则,得出分区Ⅰ—Ⅷ及全省的最优模型分别为GLO、GEV、GEV、GNO、GNO、GNO、GEV、GEV、GNO,分布参数见表4。
分区降水的相依性结构如图2所示,对角线为分区编号,左下三角的数值为两两之间的相关系数ρ,右上三角区域为两两之间的平滑拟合线和置信椭圆[25]。椭圆越圆相依性越弱,越扁相依性越强。总体上来看,分区Ⅰ—Ⅵ两两之间、分区Ⅶ与Ⅱ、Ⅲ、Ⅴ、Ⅷ之间的置信椭圆较扁,相关系数均大于0.5,降水相依性较强;分区Ⅷ与Ⅰ—Ⅵ的置信椭圆较圆,相依性相对较弱。表明广东省东部、北部及珠江三角洲地区之间的年降水量相依性强,而西部与东部、珠江三角洲地区的相依性较弱。
如图3所示,8个分区的年降水联合分布拟合P值为0.258,大于显著性检验水平0.05,经验和理论联合分布的Q-Q点据基本位于等值线附近,表明Gaussian Copula能够很好地模拟广东省分区年降水联合分布。
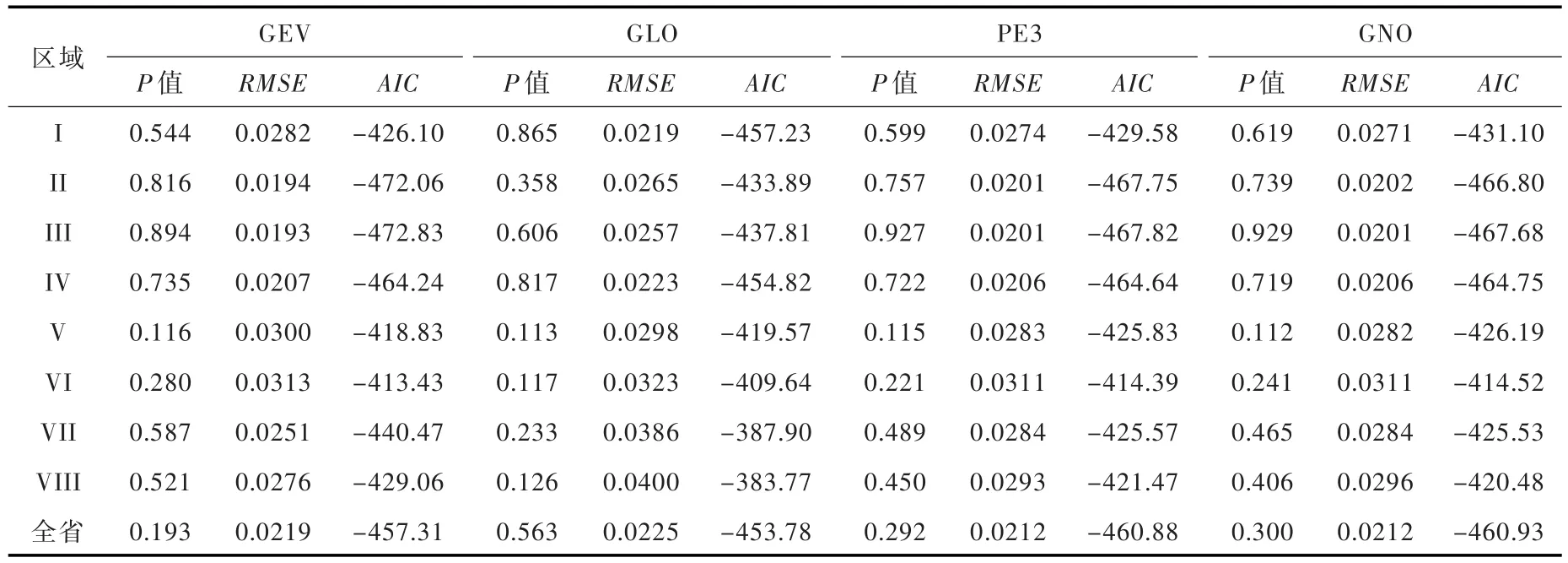
表3 年降水分布拟合检验
3.3分区降水频率组合在水资源规划中,为了反映特枯、枯水、平水、丰水、特丰的降水条件,通常关注降水频率分别为0.10、0.25、0.50、0.75和0.90的农田灌溉需水。因此将以上频率作为设定的全省降水频率,对应的典型年份分别为1958、1989、1953、1994和1961年。3种方法推求的分区降水频率组合如图4。
设定的全省频率由小到大依次对应的分区同频频率,分别为0.15、0.30、 0.51、0.71、 0.85。在平水时,同频分区频率与全省频率差别甚小,而在特枯、枯水、丰水、特丰时,两者相差均约为0.05。其中偏枯时(特枯、枯水)分区频率大于全省频率,偏丰时(丰水、特丰)分区频率小于全省频率。
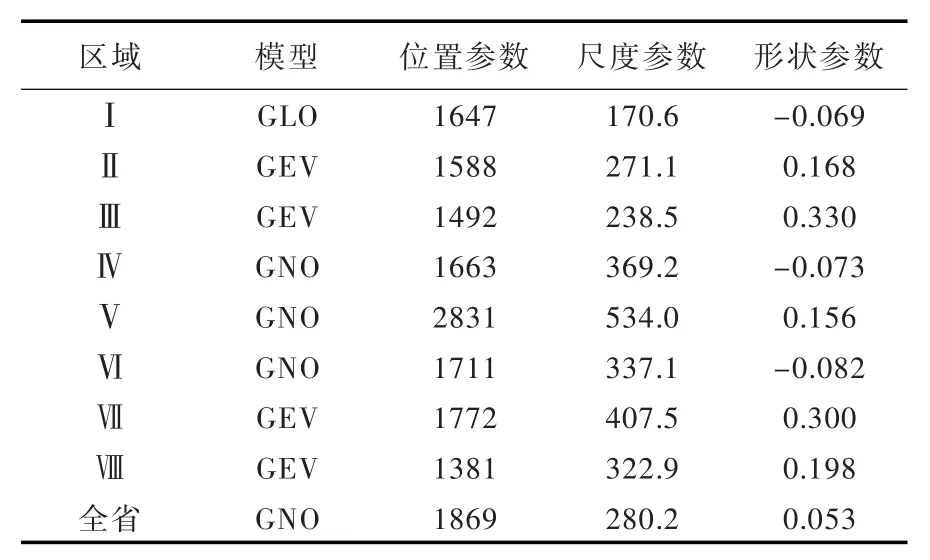
表4 年降水理论分布模型及参数

图2 分区降水相依性结构
典型年法中分区之间的频率差异明显。当设定的全省降水频率为0.25、0.5和0.75时,约一半地区低于同频频率,而另一半地区则高于同频频率。全省降水频率为0.1的特枯年时,分区Ⅰ、Ⅱ、Ⅴ和Ⅶ的降水频率更小,但分区Ⅷ降水频率较大,属于丰水年。全省降水频率为0.9的特丰年时,分区Ⅰ—Ⅵ的降水频率更大,但分区Ⅶ和Ⅷ降水频率较小,属于枯水年。

图3 分区降水联合分布拟合Q-Q图
最大权函数法推求的结果显示,大部分分区降水频率处于同频位置附近,只有分区Ⅷ的降水频率在特枯和偏丰时明显偏离同频位置。在全省降水频率为0.5时(平水年),最大权函数法分区频率置信区间的上下边界,相对于同频位置基本对称。在全省降水频率较小时(如枯水年、特枯年),置信区间偏向于大于同频频率。在全省降水频率较大时(如丰水年、特丰年),置信区间偏向于小于同频频率。分区Ⅷ的置信区间范围明显大于其他分区,表明组合推求过程中分区Ⅷ不确定性更大。其主要原因是由于分区Ⅷ和其他分区的降水相依性相对较小。

图4 分区降水频率组合

表5 广东省农田灌溉需水及分区组合
3.4农田灌溉需水全省农田灌溉需水结果(见表5)显示,3种方法之间的全省灌溉需水相差甚小。全省降水频率分别为0.1、0.25、0.5、0.75和0.9时,基于同频法的灌溉需水分别为198.4亿m3、177.3亿m3、156.5亿m3、138.3亿m3和123.9亿m3。与同频法比较,典型年法的需水相对变化分别为-2.5%、1.1%、-1.5%、0.8%和4.0%,最大权函数法的需水相对变化分别为-0.7%、0.1%、0.0%、0.5%和0.8%,其95%置信区间边界的需水相对变化分别为-2.0%~0.9%、-1.5%~1.3%、-1.0%~1.5%、-0.7%~2.0%和-0.6%~2.3%。
与同频法比较,典型年法的部分分区需水变化较大,如在全省降水频率为0.1(特枯年)和0.9(特丰年)时,分区Ⅷ需水相对变化分别达到-26.6%和37.5%,分区Ⅶ需水相对变化在全省特丰年时则达到了44.9%。相比较而言,最大权函数法的分区Ⅰ—Ⅶ需水变化较小,分区Ⅷ需水变化相对大些,前者的相对变化介于-5.1%~5.9%之间,后者约为-6.3%~14.0%。分区Ⅰ—Ⅷ的95%置信区间两端边界的需水变化差值,分别为19.4%~20.8%、18.6%~20.7%、18.1%~21.0%、25.2%~29.7%、18.5%~23.5%、30.1%~39.2%、25.9%~32.4%、30.7%~44.0%,显示分区Ⅷ需水在置信区间的取值范围明显大于其他分区。
4 结论
广东省东部、北部及珠江三角洲地区之间的年降水量相依性强,而西部与东部、珠江三角洲地区的相依性较弱。Gaussian Copula函数能够很好地模拟广东省8个农业分区年降水联合分布,分区及全省年降水最优分布主要为广义极值分布和广义正态分布。
典型年法推求的分区降水频率差异明显。最大权函数法推求的大部分分区降水频率处于同频位置附近,其中分区Ⅷ的降水频率在特枯和特丰时明显偏离同频位置,而且分区Ⅷ的置信区间范围明显大于其他分区,表明分区Ⅷ不确定性更大。
3种推求方法之间的全省农田灌溉需水相差甚小,但是分区需水差别相对较大。与同频法比较,典型年法和最大权函数法的全省需水相对变化绝对值分别在4.0%和0.8%之内,最大权函数法95%置信区间边界的全省需水相对变化绝对值不超过2.3%;典型年法和最大权函数的分区(如分区Ⅶ和分区Ⅷ)需水相对变化绝对值分别可达44.9%和14.0%,最大权函数法95%置信区间边界的分区需水变化差值,最高可达44.0%。
总之,若只要计算大尺度区域农田灌溉需水,3种方法均可以采用。但是如果需要进一步给出灌溉需水分区组合,基于高维Copula函数的联合分布模拟分析,既考虑分区降水的独立分布,又考虑了他们之间的相依性,而且能够给出分区需水的置信范围。因此可以认为,最大权函数法更为合理。
参考文献:
[1]宋悦,粟晓玲.变化环境下泾惠渠灌区净灌溉需水的响应[J].节水灌溉,2015(7):90-94.
[2]顾世祥,何大明,崔远来,等.近50多年来澜沧江流域农业灌溉需水的时空变化[J].地理学报,2010,65(11):1355-1362.
[3]刘冬梅,张京恩.浅论灌溉水库设计诉典型年法和长系列法[J].泥沙研究,2000(2):72-75.
[4]邵孝候,戴琳,钟华,等.不同水平年烤烟灌溉制度优化设计[J].中国农村水利水电,2008(5):22-24.
[5]涂新军,陈晓宏,赵勇,等.变化环境下东江流域水文干旱特征及缺水响应[J].水科学进展,2016,26(6):810-821.
[6]涂新军,陈晓宏,刁振举,等.珠江三角洲Copula径流模型及西水东调缺水风险分析[J].农业工程学报,2016,32(18):162-168.
[7]高超,梅亚东,涂新军.基于Copula函数的区域降水联合分布与特征分析[J].水电能源科学,2013(6):1-5.
[8]谢华,罗强,黄介生 .基于三维Copula函数的多水文区丰枯遭遇分析[J].水科学进展,2012,23(2):186-193.
[9]莫淑红,沈冰,张晓伟,等.基于Copula函数的河川径流丰枯遭遇分析[J].西北农林科技大学学报(自然科学版),2009,37(6):131-136.
[10]冯平,牛军宜,张永,等.南水北调西线工程水源区河流与黄河的丰枯遭遇分析[J].水利学报,2010,41(8):900-907.
[11]闫宝伟,郭生练,肖义.南水北调中线水源区与受水区降水丰枯遭遇研究[J].水利学报,2007,38(10):1178-1185.
[12]TU X J,DU X X,SINGH V P,et al.Joint risk of interbasin water transfer and impact of the window size of sampling low flows under environmental change[J].Journal of Hydrology,2017,554.doi:10.1016/j.jhydrol.2017.08.037.
[13]SALVADORI G,MICHELE C D,DURANTE F.On the return period and design in a multivariate framework[J].Hydrology and Earth System Sciences,2011,15(11):3293-3305.
[14]涂新军,杜奕良,陈晓宏,等 .滨海城市雨潮遭遇联合分布模拟与设计[J].水科学进展,2017,27(1):49-58.
[15]李天元,郭生练,闫宝伟,等.基于多变量联合分布推求设计洪水过程线的新方法[J].水力发电学报,2013,32(3):10-14.
[16]黄强,陈子燊.基于二次重现期的多变量洪水风险评估[J].湖泊科学,2015,27(2):352-360.
[17]RENARD B,LANG M.Use of a Gaussian copula for multivariate extreme value analysis:Some case studies in hydrology[J].Advances in Water Resources,2007,30(4):897-912.
[18]GENEST C,FAVRE A,BÉLIVEAU J,et al.Metaelliptical copulas and their use in frequency analysis of multi-variate hydrological data[J].Water Resources Research,2007,43(9):223-236.
[19]TU X J,SINGH V P,CHEN X H,et al.Uncertainty and variability in bivariate modeling of hydrological droughts[J].Stochastic Environmental Research Risk Assessment,2016,30(5):1317-1334.
[20]HOSKING J R M.L-Moments:analysis and estimation of distributions using linear combinations of order statistics[J].Journal of the Royal Statistical Society,1990,52(1):105-124.
[21]GENEST C,RÉMILLARD B,BEAUDOIN D.Goodness-of-fit tests for copulas:A review and a power study[J].Insurance Mathematics&Economics,2009,44(2):199-213.
[22]VOLPI E,FIORI A.Design event selection in bivariate hydrological frequency analysis[J].Hydrological Sciences Journal,2012,57(8):1506-1515.
[23]李天元,郭生练,刘章君,等.基于峰量联合分布推求设计洪水[J].水利学报,2014,45(3):269-276.
[24]广东省水利水电科学研究所.广东省一年三熟灌溉定额[M].广州:暨南大学出版社,1999.
[25]MURDOCH D J,CHOW E D.A graphical display of large correlation matrices[J].American Statistician,1996,50(2):178-180.

