黏弹性输水管道中含气瞬变流压力衰减分析
朱 炎,吴晨光,袁一星,石振锋
(1.哈尔滨工业大学 市政环境工程学院,黑龙江 哈尔滨 150090;2.哈尔滨工业大学 数学系,黑龙江 哈尔滨 150001)
1 研究背景
黏弹性管材(如:PE、HDPE、PVC等)由于其在建设和维护上的经济性,以及能够减小瞬变流过程产生的升压,被越来越多的应用到输水管线和供水管网中。按照国家“十五”规划,至2005年黏弹性管材在供水管道中的普及率将达到70%[1]。近年来,基于瞬变流原理的管道故障(漏失、堵塞等)检测技术越来越流行,研究表明通过瞬变流压力信号的频域响应可以有效的辨识管道故障类型及其位置[2-4];此外,管道故障会导致瞬变流压力衰减过程发生变化,则根据压力曲线上的异常点也可反向定位故障类型及其位置[5-6]。因此,掌握黏弹性输水管道中瞬变流压力的衰减规律十分重要。
黏弹性管道中瞬变流压力波的衰减会受到管壁摩擦、管材黏弹性、流固耦合、气穴现象(包括液柱分离和滞留气囊)、漏失或堵塞等多种因素的影响[7]。通常认为在健康的黏弹性输水管道中,瞬变流的压力衰减主要是由管壁摩擦和黏弹性效应引起的。管壁摩擦在瞬变流过程中分为稳态摩阻和非稳态摩阻两个部分[8]。在管径、管长较小的管道系统中,非稳态摩阻对瞬变流压力衰减的作用比稳态摩阻大,但在管径、管长较大的管道系统中,非稳态摩阻作用与稳态摩阻相比不再明显[9]。在黏弹性管道的单相水瞬变流过程中,黏弹性效应与管壁摩擦相比对压力衰减起着主导作用[10-12],即使在管道断面发生改变的复杂管道系统中,管壁摩擦对压力衰减的影响也可以忽略不计[13-15]。虽然基于瞬变流的故障检测技术在简单管线以及小规模流量独立计量分区的供水管网中已有应用,但其在复杂管网中的应用还存在着理论和实际方面的不足[16-17]。实际上,输水管道中由于溶解气体释放、负压抽吸等作用总会存在着少量自由气体,据报道由泵等机械设备卷入管道中的气量可达水体积的5%~10%[18]。因此,为了使基于瞬变流的故障检测技术在黏弹性输水管道中得到更好的应用,应将实际管道中可能存在少量自由气体的因素考虑在内。
本文首先通过装置实验对含气瞬变流进行研究,并在实验结果的基础上验证了基于波速修正的一维瞬变流模型的有效性。其次,基于工况模拟从能量角度分析了瞬变流过程中管壁摩擦和黏弹性效应对压力的衰减作用。再次,通过对一维瞬变流模型做傅里叶分析,从数学角度定性描述了含气率、管道系统尺度(管径壁厚比和管长)对压力衰减速率的影响。最后,研究黏弹性参数和含气率变化对压力衰减幅值和相位的影响,为瞬变流模型的参数校核提供建议。本文通过对黏弹性输水管道中含气瞬变流压力衰减规律的认识,一方面可在使用瞬变流技术检测管道故障时排除气体因素的干扰,另一方面可为黏弹性管线的设计运行提供参考。此外,模型准确是瞬变流技术用于管道故障检测的前提,因此本文关于瞬变流模型参数校核的建议对模型应用来讲意义重大。
2 实验装置与方法
如图1所示,瞬变流实验在高位水箱出口和气动蝶阀之间进行,该部分属于典型的水池-管线-阀门系统(RPV系统),稳定状态下水流从高位水箱流向低位水箱,再由水泵加压回流到高位水箱。实验装置采用有机玻璃管材(属黏弹性管材),其具体参数列于表1。实验中用精度±1%FS的超声波流量计测稳定状态下的水流流速,用量程0.16~1.6 m3/h、最小刻度间隔0.04 m3/h的气体浮子流量计计量加气量。在离高位水箱出口10.5、20.5、27.5和35.5 m的位置安装了精度0.2%、频响10 kHz、量程-10~60 m的压力传感器(如图1(a)中1—4所示)。除加气量通过肉眼读数外,水流流速和压力信号都通过研华USB-4711A数据采集卡采集并保存。

表1 实验装置参数
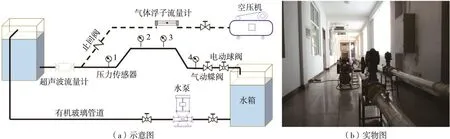
图1 实验装置示意图及实物图
在进行瞬变流实验前,首先通过电动球阀和空压机出口压力将水流流速和加气量控制到所需值,待水流流速、加气量、水箱水位稳定后,通过气动蝶阀快关来实现管道瞬变流现象。由于气动蝶阀的操作压力(0.3 MPa)远大于稳定状态下的管道内压,因此可以保证不同实验工况下的关阀时间几乎相同。由高速相机记录表明实验中每次关阀时间约为0.9 s,经计算当波速小于80 m/s时,关阀时间就会小于水锤相。瞬变流波速会随含气率而变化,则根据下文表2中的实验波速值可知,实验中的关阀时间既可能大于也可能小于水锤相。实验中水流流速和压力信号的采样率为1000 Hz,为保证信号的可靠性,所得信号后期都经过小波滤波处理。
3 瞬变流模型
3.1控制方程将管壁黏弹性效应考虑在内,一维瞬变流模型的控制方程可表示为[7-8]:
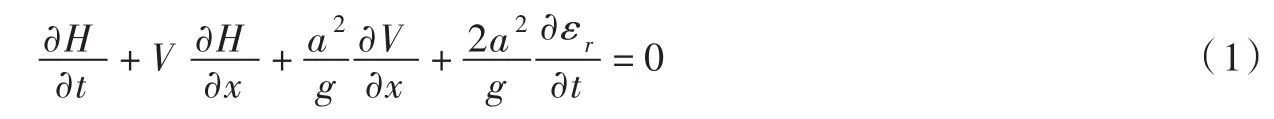

式中:H为测压管水头,m;x为沿管道轴向的空间坐标,m;g为重力加速度,m·s-2;V为气水两相混合物的流动速度,m·s-1;t为时间,s;hf为管壁摩擦造成的水头损失,无量纲数;a为瞬变流波速,m·s-1;εr为管壁的滞后应变。当管道中存在少量气体,式(1)中瞬变流波速可通过含气率修正为[19]:
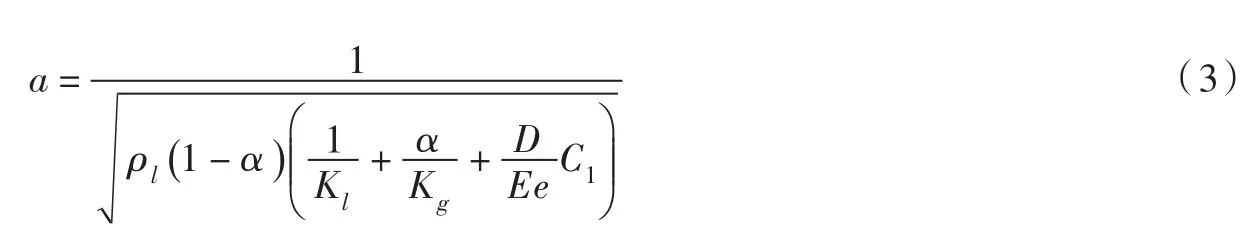
式中:ρl为水体的密度,kg·m-3;α为含气率;Kl为水的体积模量,Pa;Kg为空气的体积模量,Pa;e为管壁厚度,m;D为管道内径,m;E为管材的弹性模量,Pa。C1是与管道系统约束有关的系数,当管道系统两边完全固定时,C1可由下式计算:
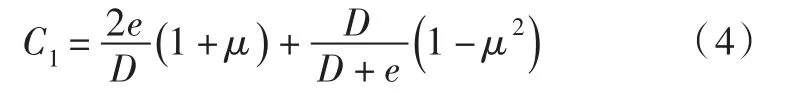
式中:μ为管材的泊松比。
由于自由气体存在使得瞬变流波速大为降低[20],导致式(1)和式(2)中的对流项不可忽略,为了保证数值求解的精度,本文采用带内插的固定网格法(如图2)来求解模型,其数值离散格式见式(5)—式(7)。
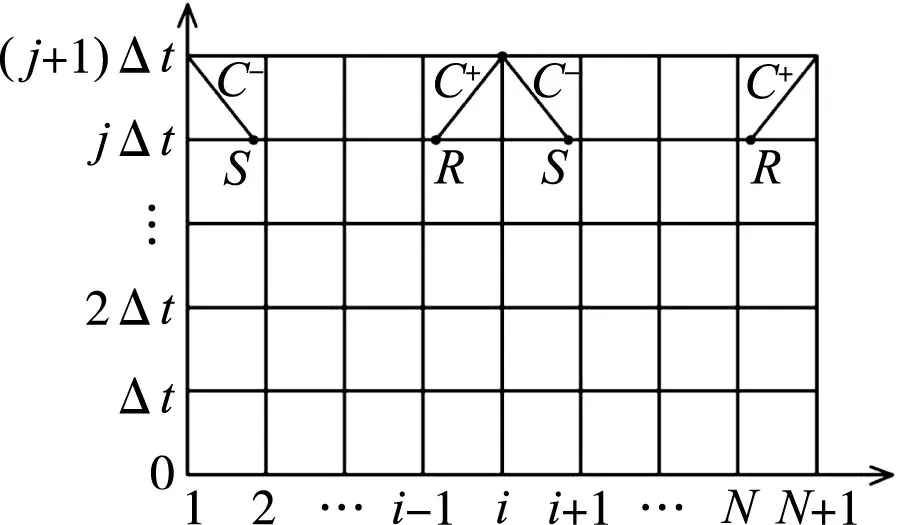
图2 带内插的固定网格法
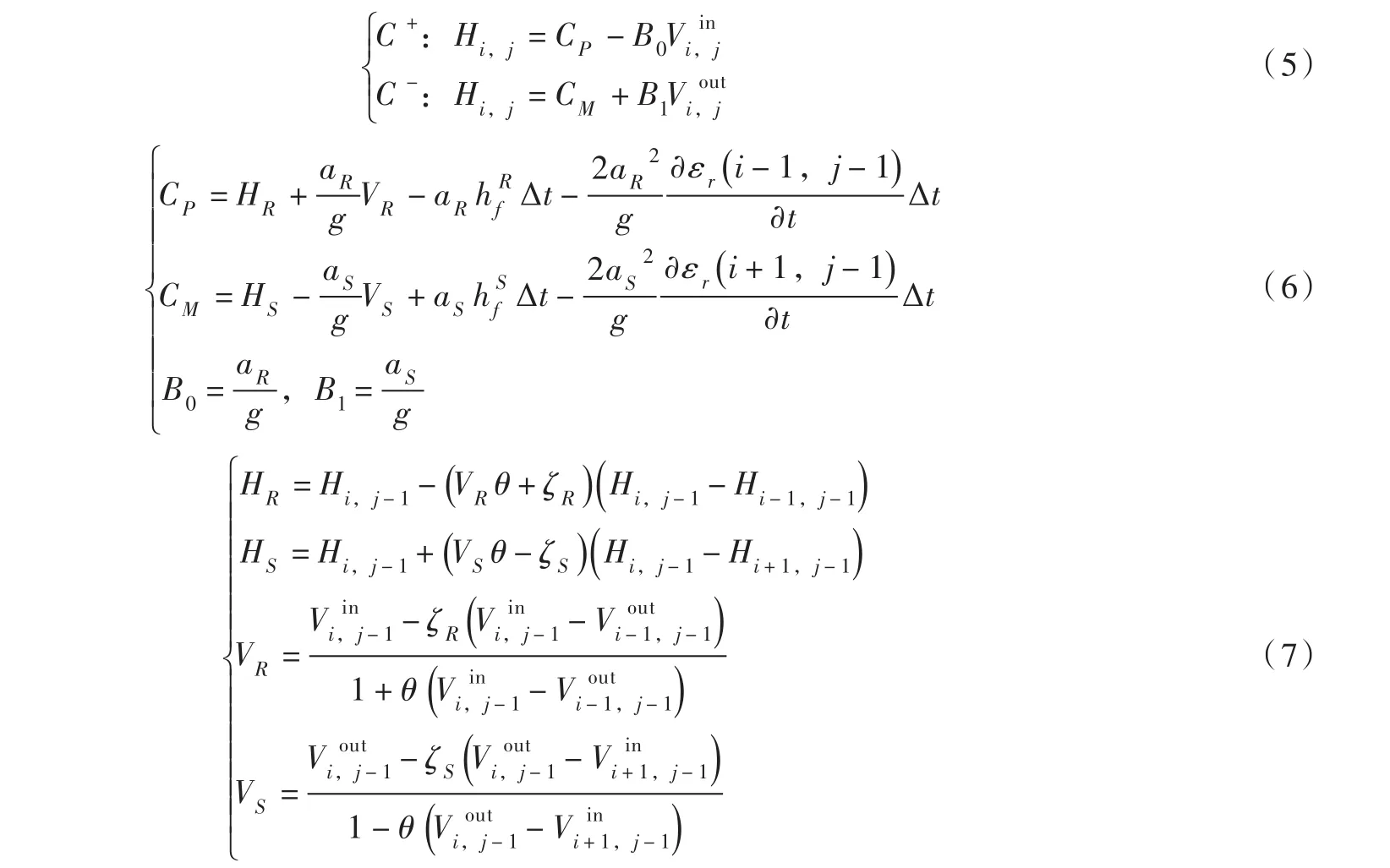
式中:i为空间节点;j为时间节点;Vin、Vout是进出空间节点的混合流体的速度;变量上、下标R和S指的是图2中矩形网格的内插节点;Δt是时间步长;θ是网格比率,θ=Δt/Δx,Δx是空间步长;ζ是内插率,ζR=ζS=θaR=θaS=θa。
3.2管壁摩擦和黏弹性效应式(2)中的管壁摩擦(hf)可分为稳态摩阻(hfs)和非稳态摩阻(hfu)两部分,其中稳态摩阻在瞬变流过程中与流态有关,其计算方式如下:

式中:f为稳定流动下的管道摩擦系数;ν为气和水两相运动黏滞系数基于α的加权平均,m2·s-1;Re为瞬变流过程中的雷诺数。非稳态摩阻的计算是流动瞬时加速度和某一加权函数W的卷积,可以按下式表示[7-8]:
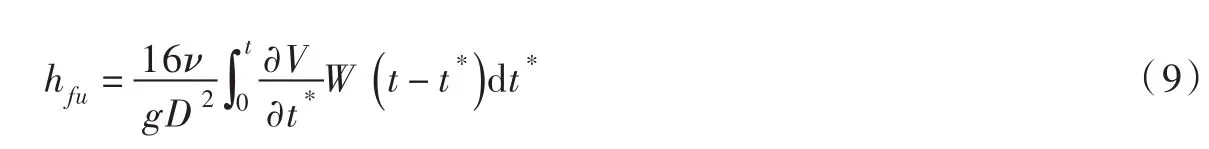
式(9)的数值离散格式如下[21]:

式中:mk和nk是由实验数据拟合得到系数,与Re有关;Δτ=KΔt,K=4ν/D2。

式中:ρ为气和水两相密度基于α的加权平均值,kg·m-3;Jk和τk为模型中对应第k组K-V元件的黏弹性参数,其单位分别为Pa-1和s;C2=C1ρgD/2e。式(13)的数值离散格式如下:

4 参数校核和模型验证
4.1参数校核由于α不同导致波速不同,而不同波速对应的黏弹性参数又有所差别[8],理论上由不同工况的实验数据校核得到的黏弹性参数有所差异。如图3所示,选择初始流速为0.9 m/s的单相水(下文表2工况6)瞬变流在4号传感器位置的实验数据来校核实验系统黏弹性参数。
本文选取3组K-V元件来描述管壁黏弹性行为,在参数校核时将τ1、τ2、τ3固定为0.05 s、0.5 s、1.5 s,通过改变J1、J2、J3将实验数据和模拟结果的前5对峰谷值做最小二乘法分析,最终得到最佳黏弹性参数如下:J1=0.00839×10-9Pa-1,J2=0.3504×10-9Pa-1,J3=0.3552×10-9Pa-1。如图 3所示,实验数据和模拟结果总体上吻合的很好,只不过在4个周期后在压力衰减相位上有所差别,这可能是因为在黏弹性参数校核时只取了实验数据和模拟结果的前5对峰谷值做最小二乘法分析。
4.2模型验证含气瞬变流实验共进行了5组不同工况,通过1—4号压力传感器的压力信号可以算出波速,将所得实验波速的均值列于表2。又将不同工况的α代入式(3)可得相应的理论波速列于表2。由表2可见,实验波速和理论波速非常接近,这说明用含气率修正的波速公式在低含气率下(至少在不大于2.37%的情况下)是适用的。
为了验证模型的有效性,选择工况4和5的实验数据与模拟结果进行对比。如图4所示,工况4和5实验压力的峰值比模拟结果略大,这可能是由于管道系统在瞬变流过程中发生微小轴向运动,管道与流体之间产生的流固耦合作用导致瞬变流升压变大。表2显示工况4和5的理论波速略小于实验波速,所以在瞬变流前3个周期内实验和模拟的压力曲线在相位上吻合得还不错,随着瞬变流过程的进行,波速误差导致的相位差不断累积,从而使得实验压力曲线相位落后于模拟结果的现象逐渐明显。根据表2和图4的结果可认为,用含气率修正波速的一维瞬变流模型可以模拟低含气率下的瞬变流过程,因此下文的能量和傅里叶分析都基于该瞬变流模型。

表2 实验与理论波速对比
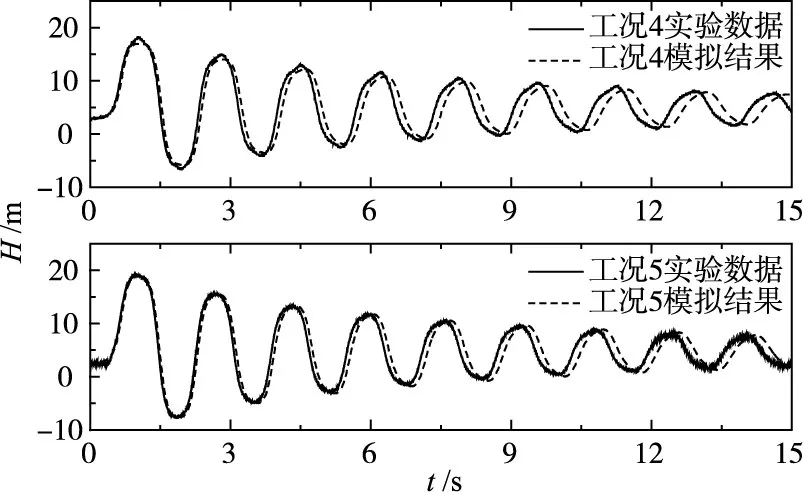
图4 实验数据与模拟结果对比
5 结果与讨论
5.1能量分析通过能量分析可以清晰的看出输水管道中不同含气率下管壁摩擦和黏弹性效应对瞬变流压力衰减的影响。由于表2中实验工况的水流流速都不相同,在此基于实验装置选择3种初始流速相同、含气率不同、关阀时间都为0.9 s的模拟工况进行能量分析,其初始工况参数分别为:V=0.9 m/s,α=0;V=0.9 m/s,α=0.5%;V=0.9 m/s,α=1%。在瞬变流过程中,管壁摩擦对水体的做功效率可表示为[11]:

式中:A为管道截面积,m2;τw代表瞬变流过程中的管壁摩擦力,kg·m-1·s-2。为了研究方便,稳态摩阻和非稳态摩阻的共同作用的管壁摩擦可简化为[22]:

根据式(17)和式(18),将3种模拟工况在4号传感器位置管壁摩擦的做功效率绘于图5。
如图5所示,在单相水瞬变流中,由于黏弹性效应造成的压力衰减太快[11-12],瞬变流持续过程很短,因此管壁摩擦做功时间也很短,并且在关阀完成后(0.9 s后),流速很快降到0附近,所以在关阀完成后管壁摩擦做功也很少。随着α的增大,管壁摩擦做功效率也增大,这主要由两方面原因引起:(1)当α<50%时,稳态摩阻的摩擦系数会随着α的增大而变大,导致稳态摩阻部分的做功变大[23];(2)管壁摩擦引起的压力衰减速率会随着α的增大而变大,这一点将在5.2节中加以证实。
水体对管壁的做功效率(与管壁对水体做功效率相反)可表示为[11]:

式中:qR为管壁的径向速度,m/s,其与式(1)中黏弹性项存在以下关系[11]:

根据式(19)和式(20),将3种模拟工况在4号传感器位置水体对管壁的做功效率绘于图6。
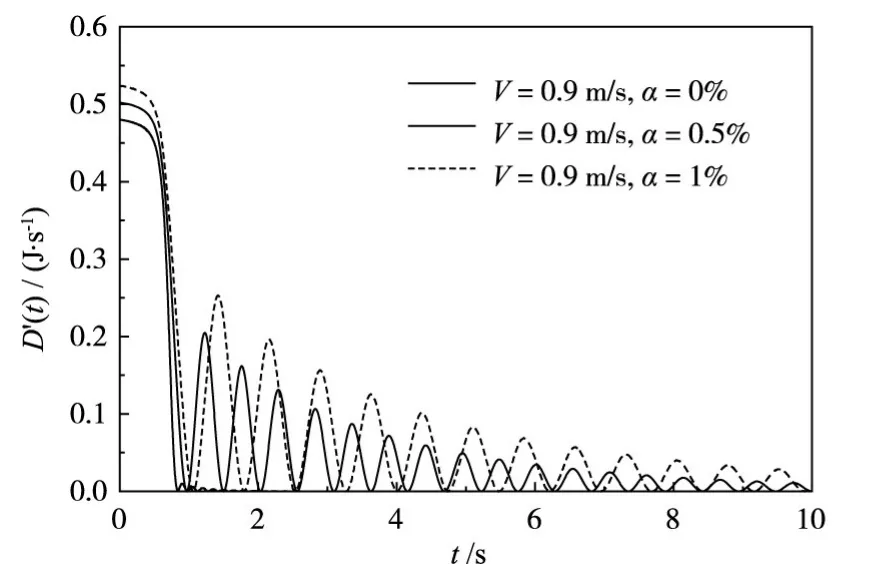
图5 含气率对管壁摩擦做功效率的影响

图6 含气率对水体做功效率的影响
如图6所示,水体对管壁所做功有正有负,正值代表管道中的正压波造成管壁膨胀,负值代表管道中的负压波引起管壁收缩。图6中曲线正值部分面积减去负值部分面积之差就是由于黏弹性效应引起的能量消耗。对比α为0%和0.5%的工况发现,含气瞬变流中水体对管壁做功效率明显较小,导致黏弹性效应造成的能量损失也小的多,从而瞬变流压力衰减的整个过程也相应延长。这是因为自由气体存在造成水的体积模量变小,则水体在受到正压力波时体积膨胀减小,从而导致管壁的形变也变小,所以气体存在使得黏弹性效应对压力衰减的作用大为减弱。而对比α为0.5%和1%的工况,难以确定哪个工况的黏弹性效应造成的能量消耗更大,但可以看见水体对管壁做功的幅值随着α增大而变小,这说明管壁形变随着α增大而减小,则理论上由于管壁形变(即黏弹性效应)造成的能量消耗也应该变小,这一点也会在5.2节中加以印证。
5.2傅里叶分析为了进一步从数学角度解释含气率以及管道系统尺度对瞬变流压力衰减的影响,本文通过对一维瞬变流模型做傅里叶分析,得到关于管壁摩擦和黏弹性效应引起的压力衰减速率的表达式。根据表2中工况1的含气率,当水流流速为2 m/s时,水流流速占波速比例约为3%(二者相差一个数量级),因此在低含气率下用傅里叶变换定性分析瞬变流压力衰减时,可对控制方程做一些简化:(1)可忽略控制方程中的对流项;(2)黏弹性效应的计算只取一组黏弹性参数(J和τ);(3)管壁摩阻作用以简化后的管壁摩擦来代替。对简化后的式(1)和式(2)做傅里叶变换,再经过合并得到关于压力频域函数的偏微分方程:

式中:C3=16ν/gD2,C4=ω2/a2+2C2Jω2/g(iωτ+1),C5=2iωC2J/(iωτ+1),C6=ω2/a2-16iων/a2D2;ω是压力波的频率,ω=a/2L。式(15)的通解为:

式中:C7为依赖于系统边界条件的系数;λ是对应式(21)的特征值方程的解,通常可表示为λ=Kr+iKi,其中Kr是与压力衰减速率相关的参数,Ki是与频域相位变化率相关的参数。如果将管壁摩擦和黏弹性效应引起的压力衰减单独考虑,当不考虑黏弹性效应时(即J=τ=0),根据式(21)的特征值方程求解可得到由管壁摩擦引起的压力衰减速率(Kr-PF)为:
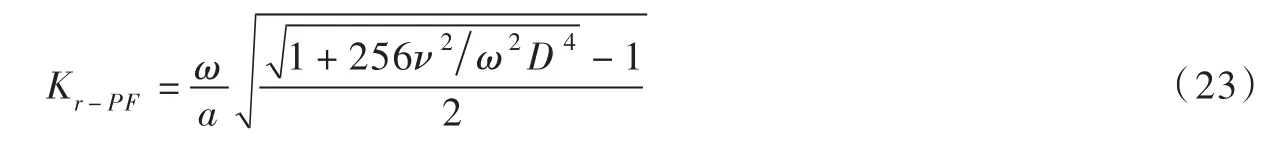
同样,当不考虑管壁摩擦时(即ν=0),得到由黏弹性效应引起的压力衰减速率(Kr-VE)为:
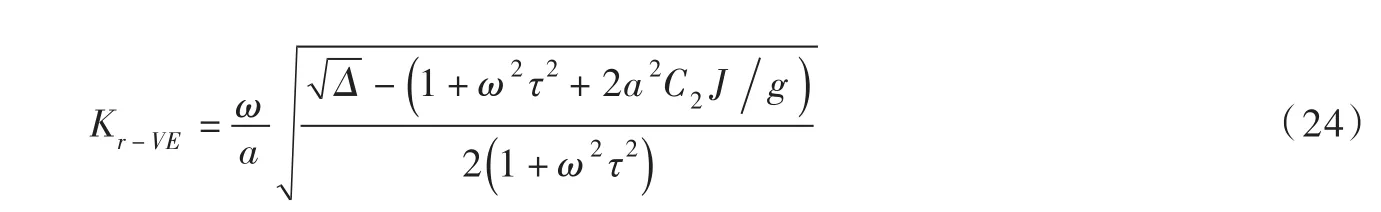
将式(23)和(24)对波速(a)和 波频率(ω)求一阶导可得:∂Kr-PF/∂a< 0, ∂Kr-PF/∂ω> 0, ∂Kr-VE/∂a>0和∂Kr-VE/∂ω>0。此外,将波速a对α和管径壁厚比(β=D/e)求一阶导可得:
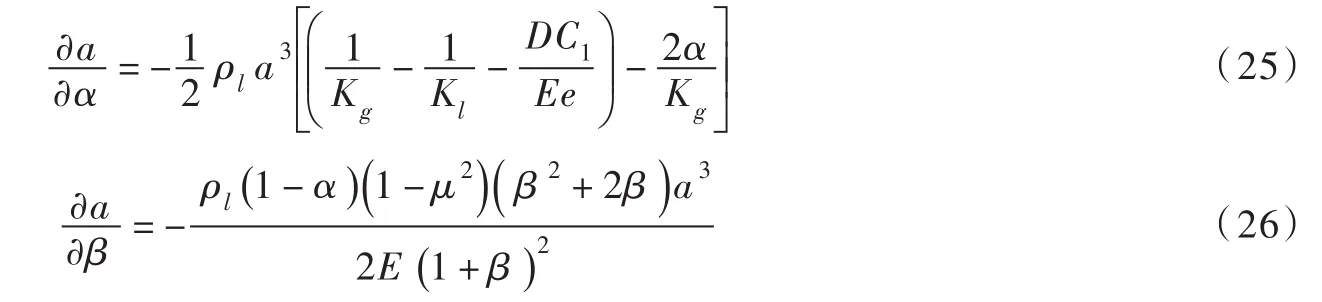
式(25)中,由于Kl=2.1×109Pa,Kg在低压系统可看作一个标准大气压,则1/Kl和DC1/Ee与1/Kg相比可以忽略不计,因此当α≤ 50%时,∂a/∂α≤ 0;当α≥ 50%时,∂a/∂α≥ 0。式(26)中,因为α≤ 1和μ≤ 1,所以∂a/∂β<0,则将Kr-PF和Kr-VE对α和β进一步求一阶导可得:
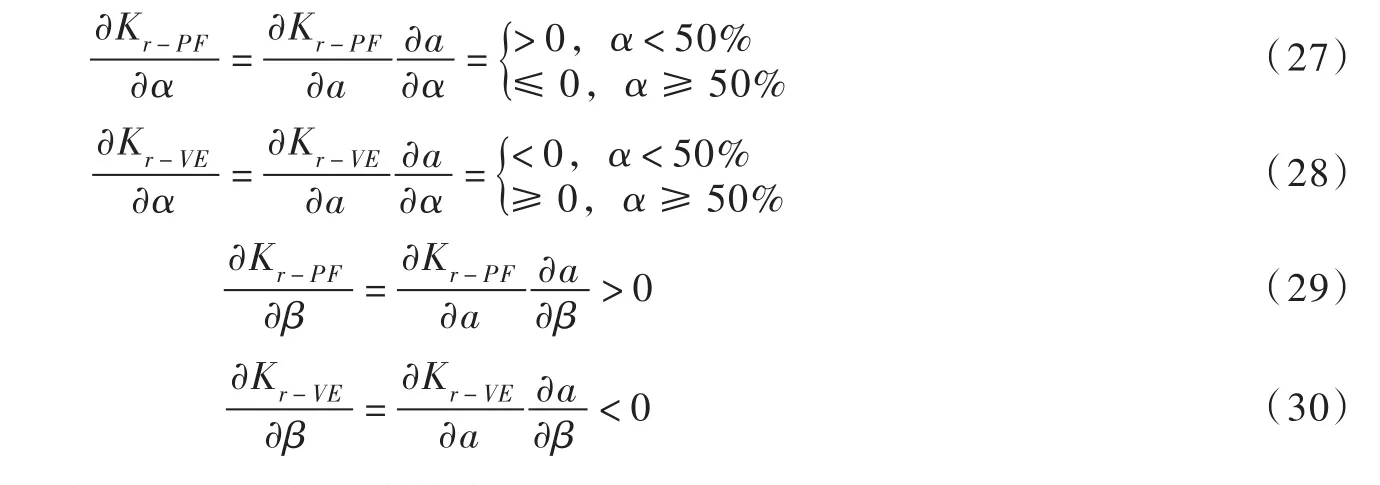
此外,当波速保持不变时,Kr-PF和Kr-VE对L的一阶导为:

由于傅里叶分析是基于低含气率的假设,且输水管道中含气率一般远小于50%,则由式(27)和式(28)可知,在黏弹性输水管道中,由管壁摩擦引起的压力衰减速率随着含气率的增大而增大,由黏弹性引起的压力衰减速率随着含气率的增大而减小,这也印证了能量分析得到的结论。由式(29)和式(30)可知,管径壁厚比越大,由管壁摩擦引起的压力衰减速率越大,而由黏弹性引起的压力衰减速率越小,也就是说在管径、管长较大的管道系统中管壁摩擦有可能比黏弹性效应对压力衰减的作用更显著。由式(31)和式(32)可知,管壁摩擦和黏弹性效应引起的压力衰减速率都会随着管长的增加而变大,所以在设计黏弹性输水管线时,黏弹性管段越长越有利于瞬变流压力的衰减。
5.3参数校核建议管壁的黏弹性行为受管材分子结构、温度、管道约束、压力加载过程等因素的影响,通常由材料力学实验确定的黏弹性参数可用于管线设计阶段[26]。为了将瞬变流技术用于黏弹性管道的故障检测,需要通过实测数据对黏弹性参数进行校核。由前文分析可知,在含气瞬变流中黏弹性效应会由于气体存在而大为削弱,因此当含气率超过某一值时,黏弹性参数对瞬变流的影响就不再重要,在模型校核时就不必对其进行校核。
图7以本文实验管材、文献[24]中的HDPE管材这两种黏弹性管材为例,研究含气率对瞬变流波速的影响。如图7所示,在α<0.2%的范围内,波速对含气率变化非常敏感,此时波速主要受管道断面尺寸和管材属性参数影响。当α>0.2%时,随着含气率增加,两种管材对应的波速曲线逐渐趋于重合,这是因为此时含气率对波速起决定作用,且大大超过了管道断面尺寸和管材属性参数对波速的影响。当α>1%时,波速下降速率变慢,两种管材对应的波速曲线几乎重合,因此当α>1%时,管道断面尺寸和管材属性参数对波速的影响很小。
为了进一步分析含气瞬变流中气体影响的重要性,以本文实验装置为基础,在工况α=1%的基础上,研究黏弹性参数和含气率变化对瞬变流压力衰减的影响。通常埋地黏弹性管道由于约束、温度等原因,弹性模量会变小,相应的黏弹性参数也会变小,但减小幅度不会很大[24]。因此,在研究黏弹性参数变化对瞬变流压力衰减影响时,将实验系统参数τ1、τ2、τ3保持不变,J1、J2、J3缩小一个数量级。图8中J代表实验系统的黏弹性参数,J′代表将其缩小后的黏弹性参数。
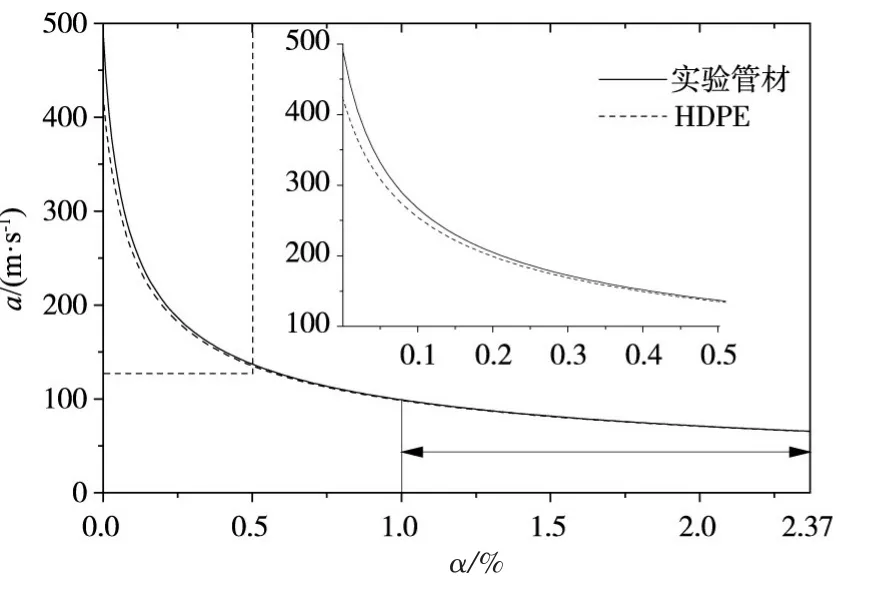
图7 含气率对瞬变流波速的影响

图8 黏弹性参数和含气率变化对瞬变流压力衰减的影响
如图8所示,当α=1%时,在前6个周期(10 s)内,由黏弹性参数J′和J计算所得压力峰值之间的平均相对误差约为10%。由前文可知,在真实管道中黏弹性效应对压力的衰减作用会进一步削弱,因此α=1%时,在实际中由黏弹性参数减小引起压力幅值的变化实会更小。由图8还可看出,在α=1%的基础上含气率增加0.1%对压力衰减幅值的影响与黏弹性参数减小带来的影响相当,但压力衰减相位却变化明显。一般来讲,在单相水瞬变流中黏弹性效应会导致压力衰减相位发生偏移[17],而图8显示在α=1%时,黏弹性参数减小对压力衰减相位的偏移作用远不如含气率变化带来的影响。
综合图7和图8的结果,当α>1%时,含气率变化对压力衰减过程的影响比黏弹性参数减小产生的影响要大得多。在用瞬变流技术检测黏弹性管道故障时,可先根据实验数据得到瞬变流波速,再根据式(3)反求得到输水管道中的含气率,从而可建议:当α<1%(更接近单相水流动)时,模型校核时不仅要对波速和稳态摩阻进行校核,还要对黏弹性参数进行校核;当1%≤α≤2.37%时,只需对波速和稳态摩阻进行校核,黏弹性参数对模型的影响不再重要。鉴于本文实验中含气率最大为2.37%,因此,关于更高含气率下模型的有效性以及基于模型所得的推论,还需要进一步验证。
6 结论
本文通过装置实验对一维含气瞬变流模型进行验证,并基于模型从能量和傅里叶分析的角度对黏弹性输水管道中含气瞬变流的压力衰减进行了研究,还比较了黏弹性参数和含气率变化对瞬变流压力衰减的影响,得到以下结论。
(1)在低含气率下(α≤2.37%),用含气率修正的波速公式来计算波速是准确的,且基于波速修正的一维瞬变流模型可以模拟低含气率下的瞬变流过程。
(2)含气瞬变流中黏弹性效应对压力衰减的作用大为削弱,使得瞬变流压力衰减变慢。当黏弹性输水管道中α≤2.37%,随着α和β增加,由管壁摩擦引起的压力衰减速率变大,而由黏弹性效应引起的压力衰减速率则变小,但两者都会随着管道长度的增加而变小。
(3)在用瞬变流技术检测黏弹性输水管道故障时,建议当α<1%时,不仅要对波速和稳态摩阻进行校核,还要对黏弹性参数进行校核;当1%≤α≤2.37%时,只需对波速和稳态摩阻进行校核。
参考文献:
[1]建设部.国家化学建材产业“十五”计划和2010年发展规划纲要[J].辽宁建材,2001(1):3-7.
[2]郭新蕾,杨开林.管道泄漏检测的水力瞬变全频域数学模型[J].水利学报,2008,39(10):1264-1271.
[3]郭新蕾,杨开林,郭永鑫,等.管道泄漏检测全频域法试验验证及抗噪性研究[J].水利学报,2011,42(6):713-720.
[4]刘志勇,刘梅清,蒋劲,等.基于瞬变流频率响应分析的输水管道泄漏检测[J].水利学报,2015,46(11):1352-1359.
[5 ]BRUNONE B,FERRANTE M.Detecting leaks in pressurised pipes by means of transients[J].Journal of Hydraulic Research,2001,39(5):539-547.
[6]MENICONI S,BRUNONE B,FERRANTE M,et al.Anomaly pre-localization in distribution-transmission mains by pump trip:preliminary field tests in the Milan pipe system[J].Journal of Hydroinformatics,2015,17(3):377-389.
[7 ]BERGANT A,TIJSSELING A S,VÍTKOVSKÝ J P,et al.Parameters affecting water-hammer wave attenuation,shape and timing—Part 1:Mathematical tools[J].Journal of Hydraulic Research,2008,46(3):373-381.
[8]COVAS D,STOIANOV I N,MANO J F,et al.The dynamic effect of pipe-wall viscoelasticity in hydraulic transients.Part II—Model development,calibration and verification[J].Journal of Hydraulic Research,2005,43(1):56-70.
[9]DUAN H F,GHIDAOUI M S,LEE P J,et al.Relevance of unsteady friction to pipe size and length in pipe fluid transients[J].Journal of Hydraulic Engineering,2012,138(2):154-166.
[10]SOARES A K,COVAS D I,REIS L F.Analysis of PVC pipe-wall viscoelasticity during water hammer[J].Journal of Hydraulic Engineering,2008,134(9):1389-1394.
[11]DUAN H F,GHIDAOUI M S,TUNG Y K.Energy analysis of viscoelasticity effect in pipe fluid transients[J].Journal of Applied Mechanics,2010,77(4):044503.
[12]DUAN H F,GHIDAOUI M,LEE P J,et al.Unsteady friction and visco-elasticity in pipe fluid transients[J].Journal of Hydraulic Research,2010,48(3):354-362.
[13]MENICONI S,BRUNONE B,FERRANTE M.Water-hammer pressure waves interaction at cross-section changes in series in viscoelastic pipes[J].Journal of Fluids and Structures,2012,33:44-58.
[14]MENICONI S,BRUNONE B,FERRANTE M,et al.Transient hydrodynamics of in-line valves in viscoelastic pressurized pipes:long-period analysis[J].Experiments in Fluids,2012,53(1):265-275.
[15]MENICONI S,BRUNONE B,FERRANTE M,et al.Energy dissipation and pressure decay during transients in viscoelastic pipes with an in-line valve[J].Journal of Fluids and Structures,2014,45:235-249.
[16]STEPHENS M L.Transient response analysis for fault detection and pipeline wall condition assessment in field water transmission and distribution pipelines and networks[D].Adelaide:University of Adelaide,2008.
[17]STEPHENS M L,LAMBERT M F,SIMPSON A R,et al.Calibrating the water-hammer response of a field pipe network by using a mechanical damping model[J].Journal of Hydraulic Engineering,2011,137(10):1225-1237.
[18]POZOS O,GONZALEZ C A,GIESECKE J,et al.Air entrapped in gravity pipeline systems[J].Journal of Hydraulic Research,2010,48(3):338-347.
[19]WYLIE E B,STREETER V L,SUO L.Fluid Transients in Systems[M].Englewood Cliffs,NJ:Prentice Hall,1993.
[20]WIGGERT D C,SUNDQUIST M J.The effect of gaseous cavitation on fluid transients[J].Journal of Fluids Engineering,1979,101(1):79-86.
[21]VÍTKOVSKÝ J P,STEPHENS M,BERGANT A,et al.Efficient and accurate calculation of Zielke and Vardy-Brown unsteady friction in pipe transients[C]//Proceedings of the 9th International Conference on Pressure Surges,2004:405-419.
[22]GHIDAOUI M S,ZHAO M,MCINNIS D A,et al.A review of water hammer theory and practice[J].Applied Mechanics Reviews,2005,58(1):49-76.
[23]LOCKHART R W,MARTINELLI R C.Proposed correlation of data for isothermal two-phase,two-component flow in pipes[J].Chemical Engineering Progress,1949,45(1):39-48.
[24]COVAS D,STOIANOV I,RAMOS H,et al.The dynamic effect of pipe-wall viscoelasticity in hydraulic transients.Part I—Experimental analysis and creep characterization[J].Journal of Hydraulic Research,2004,42(5):517-532.

