水工结构数值仿真等几何分析方法初探
李明超,张梦溪
(水利工程仿真与安全国家重点实验室,天津大学,天津 300354)
1 研究背景
在水利工程中,数值仿真计算已成为工程设计和运行评价的重要环节,对于结构和边界复杂的重力坝、拱坝等水工结构,常采用有限元分析(Finite Element Analysis,FEA)求解计算[1-4]。FEA方法需将计算机辅助设计(Computer Aided Design,CAD)建立的几何模型,导入计算机辅助工程(Computer Aided Engineering,CAE),并利用有限元进行工程分析。但实际上,几何模型与分析模型之间在概念和技术层面均存在较大差异[5]。二者建立基于两个不同的平台,分析模型由几何模型简化与网格离散化处理后形成,但这一过程不但会舍弃精细的几何信息,造成求解失真,而且复杂耗时。据美国Sandia国家实验室统计,整个仿真分析过程约80%时间用于模型操作与网格划分,仅20%用于求解分析[6]。“精细化”分析是数值仿真的趋势所在,“高效率”又是大型工程问题求解的必然要求,而水利工程地形条件不规则、水工建筑物体量庞大、各部件尺度不一,导致传统有限元建模方法繁琐耗时,且需要进行大量的简化,模型间信息的单向传输更是增加了网格修改的难度。因此,有限元分析在一定程度上已难以满足水工结构“精细化”与“高效率”分析的要求。
为实现CAD与CAE的集成统一,Hughes等[7]以计算机辅助设计的样条基函数作为形函数提出了等几何分析(Isogeometric Analysis,IGA)的思想,将传统的有限元方法中的几何模型和分析模型统一到同一个平台,无需二次离散建模,不仅省略了耗时较多的自定义网格剖分过程,而且将设计模型中的几何连续性保留到计算物理场中,提高了数值解的精度,节省了计算自由度。等几何分析方法一经提出便引起广泛关注,其理论研究已取得较大进步,主要体现在:几何造型的样条理论[6]、控制网格的局部细化策略[8]、曲面裁剪与拼接[9]、数值积分方案[10]以及边界条件施加[11-12]等技术的不断发展;为发挥IGA的求解优势,国内外学者开发了基于等几何分析的CAE软件平台[13-14],并成功地将等几何方法与有限元方法结合计算[15-16]。目前,等几何方法已成功应用于接触分析[17]、流体力学[18]、结构优化[19]等多类物理问题的求解。在水利工程领域,张勇等[20]将等几何分析的思想引入比例边界有限元中,提出了比例边界等几何方法,并将其应用于大坝的地震响应分析与求解。总之,等几何分析(IGA)的提出实现了几何模型与分析模型的同一表达,在求解过程中相对于传统有限元分析(FEA)优势明显,具有较高的工程应用价值。非均匀有理B样(Non-Uniform Rational B-Spline,NURBS)函数比传统的网格建模方式能够更好地控制物体表面的曲线度,为处理复杂模型形状提供了极大的灵活性和精确性,目前,基于NURBS的参数化建模技术已成功解决水工结构、复杂地质地形的精细化几何建模问题[21],但是等几何分析方法在水利工程领域应用较少,该方法的能否同时实现“精细化”与“高效率”的建模与求解需要进一步验证,围绕等几何分析思想展开的水利工程领域数值模拟有待深入。
考虑到NURBS技术的精细化建模特性与等几何分析方法的高效率集成特性,以NURBS模型为基础,对等几何分析方法在水工结构数值仿真分析的适用性进行探索,通过消除有限元方法几何模型与分析模型间的差异,为解决考虑复杂地形地质条件下的大型水工结构建模与仿真计算难以有效耦合的问题提供了新的手段。通过对比IGA与FEA基本思想、网格模型生成等过程的差异,展示了IGA在建模过程的“精细化”与“高效率”的优势;进而以混凝土重力坝数值计算为例,建立适用于等几何分析的多片几何模型,改变模型的单元密度,分别从“计算精度”和“仿真效率”两个方面对比分析IGA与FEA的仿真计算结果,来验证IGA建模与计算分析的“精细化”与“高效率”。
2 等几何分析与有限元分析方法对比
2.1等参元分析思想在利用有限元方法求解实际工程问题时,通常采用不规整单元离散逼近形状不规则的几何模型,但直接计算不规整单元比较困难,需利用坐标系变换、单元映射等技术,通过几何规整单元(如:矩形单元、正六面体单元等)推导对应几何不规整单元的计算结果[22],如图1所示,基于图1左图进行简便的数值积分等计算,随后将其计算结果映射到图1右图中,即得到求解区域的数值解。为解决CAD/CAE的集成问题,消除几何模型与分析模型间的差异,同时考虑到等参概念可应用于包括B样条和NURBS函数在内的多种几何建模函数,因此,Hughes等[7]提出采用几何建模的样条基函数(如:NURBS、T样条等)建立精确的几何模型,并使用相同的样条基函数作为解空间的基函数进行求解,这就是等几何分析的等参元思想[7,23]。等参元思想的引入,将待求解的物理量(如位移、温度等)表示为与几何模型描述相同的基函数的表现形式,实现了几何模型与分析模型的统一。

图1 矩形单元映射为任意四边形单元[22]
传统有限元方法在应用时同样采用等参元的思想,IGA与FEA等参元思想主要区别在于:(1)FEA首先采用多项式基函数逼近未知解,再利用该基函数逼近已知的几何模型,而IGA则先建立精确几何模型,再利用建立几何模型的基函数进行求解;(2)FEA求解过程中使用的基函数和网格离散后的分析模型通过分段多项式来定义,IGA方法在几何建模和求解分析时使用相同的样条基函数,实现了几何模型与分析模型的同一表达;(3)FEA的等参变换是基于单元之间的映射,见图1,而IGA的等参变换是基于整个区域间的映射,区域内往往包括多个等几何单元(见图2),这样就降低了映射的个数,减少了计算量,单元间的连续同时提升了区域内数值解的连续性。
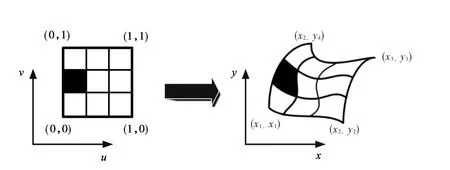
图2 矩形参数域映射为模型域
2.2计算分析过程差异同传统的数值分析方法一样,等几何分析仍是通过前处理、求解计算和后处理三个过程得到偏微分方程的近似解。FEA与IGA的求解流程如图3所示[6],二者差异主要体现在:(1)利用计算机辅助设计(CAD)构造适合分析的几何模型(Analysis Suitable Geometry,ASG)后,通过前处理将ASG模型进行网格离散时,FEA需经过二次建模过程生成有限元网格,而IGA网格在建模时自动生成,可节省大量的分析时间;(2)FEA的网格离散是利用近似几何对求解域进行逼近,IGA则是对求解域的精确几何表达,二者网格离散后主要区别如表1所示;(3)利用IGA与FEA求解后,通过后处理手段来检查计算精度,若不满足要求,则需对分析模型的网格细化处理,但两种方法网格细化应用的对象不同,FEA在网格细化时需更改ASG模型,且信息为单向传递,修改模型复杂耗时,而IGA只需对分析模型进行操作即可,无需重复前处理的过程,极大地提高了仿真效率。

图3 FEA与IGA仿真分析过程[6]

表1 IGA与FEA主要区别
3 基于NURBS建模的等几何分析算法
3.1NURBS模型
3.1.1基础几何模型CAD几何表示主要有显式、隐式以及参数化等表示方法,其中,参数化表示因其良好的适用性和可操作性已成为主要建模方式[23-24]。NURBS是目前几何建模应用最广的参数化函数,故考虑将其作为等几何分析的基函数。NURBS建模以节点向量和控制点的计算为核心,其中节点向量由一组非递减的实数组成,用来描述曲线参数空间的参数,定义为n为基函数(控制点)个数,p为B样条的阶数。B样条基函数通过递推公式定义如下[7,23]:

为实现精确表示几何模型,在B样条的基础上,引入权因子ωi,通过有理化方式构造出NURBS,其基函数定义如下[7,23]:

如图4(a)所示,对于给定的n次样条和节点向量I,可构建n个p阶NURBS基函数,将n个控制顶点Pi与 NURBS基函数线性组合可确定p阶 NURBS曲线为[7,23-24]:

对于二维模型,给定一张n×m的网格控制顶点Pij(i=1,2,…,n;j=1,2,…,m);节点矢量如图4(b)所示,可确定NURBS曲面为[23]:

如图4(c)所示,给定n×m×l个控制顶点Pijk(i=1,2,…,n;j=1,2,…,m;k=1,2,…,l)与相应的节点矢量NURBS实体可通过下式定义[23]:


图4 NURBS几何模型
3.1.2多片几何模型在实际情况下,单个NURBS曲面片难以处理材料介质不均匀以及截面形式复杂的多连通区域问题,即使能够只用一个NURBS片表示几何模型,由于几何本身的结构变化,也可能形成极端扭曲的网格,并影响单元计算。因此,有必要利用多个NURBS片拼接定义几何模型,而将其拆分为多个片,能够有效减少扭曲单元,形成更加自然光滑的网格。
多片等几何模型建立的基本思想为:求出每块NURBS曲面片的系数矩阵,再通过连通数组将其组装成总体系数矩阵。如图5所示,为两个NURBS曲面片的拼接,上标代表该控制点所属的面片,下标f代表交接处的控制点,下标n代表非交接处的控制点。则控制点可表示为[6]:

若通过插入节点对面片2细化处理,则细化后控制点可表示为[7]:


因此,为满足面片交接处连续,对于两个NURBS曲面片控制点处的位移应满足:


图5 NURBS模型面片拼接
3.2IGA建模
3.2.1等几何离散建模网格离散是前处理的关键一环,需将求解域离散为多个单元。传统的数值方法的计算分析模型均通过操作几何模型,进行二次建模得到,这一过程不仅需要较大的工作量,而且会丢失原有模型的几何特征,尤其是自定义单元在单元连接处将会丧失原有的几何连续性,直接影响求解的精度。不同于FEA,等几何离散生成的NURBS单元为参数化建模时自动生成,并非二次建模时生成,每一个NURBS单元都对应参数域中一个非零跨距的节点区间。如图6所示,以双二次的NURBS单元为例,将矩形模型离散为4个NURBS单元,每个单元与9个控制点关联,相邻两个NURBS单元共用6个控制点。利用等几何模式对几何模型离散,既能使单元间保持高阶连续,又节省了二次建模的过程,计算分析模型可直接继承于前处理中的设计模型(几何模型)。

图6 等几何离散生成的双二次NURBS单元
3.2.2网格细化为提高求解精度,需对分析模型的控制网格精细化处理,NURBS模型网格细化方式主要有h-细化、p-细化和k-细化三种策略,细化过程中几何表达不变,但插值位置和连续性有所区别。h-细化是运用节点插入方法在原节点矢量中插入新的节点值,将几何形体的单元尺寸缩小,使模型参数域的自然网格面片和模型控制点增多,从而实现模型网格细化;p-细化是保持原网格固定的情况下,提升基函数的阶数,对原有节点矢量的节点值进行相应的重复,以改善求解精度;k-细化是基于节点插入(h-细化)和基函数升阶(p-细化)而提出的网格细化方法,是属于等几何分析特有的网格细化方法。图7所示为k-细化过程中基函数的变化情况,将线性单元通过先升阶后插值的方式细化为二次单元,且单元间保持C1连续性。

图7 k-细化策略基函数变化过程
在有限元分析中,网格离散主要是对求解区域进行逼近,在网格密度较小的情况下,分析模型与几何模型差异较大,尤其是对于包含曲线的求解区域,分别建立不同密度的1/4圆环网格模型如图8所示,曲线部分被简化为多段直线,失去了几何的精确性,随着网格密度的增加,多段直线才趋近于曲线。因此,针对复杂的水工结构、地质模型进行分析时,FEA建模难度大、网格离散后精度有限、模型调整复杂耗时等缺陷愈发明显。相比而言,等几何分析离散的分析模型均是对求解区域的精确几何表达,且在网格细化过程中,仅在几何模型内部进行节点插入和基函数升阶等操作,不改变几何外形,网格细化后的模型可直接求解计算,节省了大量复杂繁琐的工作,可以说等几何分析在前处理过程中消除了FEA几何模型与分析模型在几何表达方面的差异,弥补了FEA建模的缺陷。

图8 网格细化分析模型变化情况
3.3IGA单元分析与整体分析通过等几何离散得到分析模型后,与FEA原理相近,首先对单元进行分析,以位移为例,根据等参元思想,将变量场描述为[20,22]:

式中:ue为单元位移场;Ne为单元几何形状矩阵;qe为单元控制点位移列阵。
将单元的势能对qe取一阶极值,得到单元刚度方程为[20,22]:

单元刚度矩阵可表示为[20]:

等效荷载矩阵为面力项Pte与体力项之和[20]:

式中:Be为单元几何函数矩阵;D为弹性系数矩阵;分别为面荷载与体荷载。
将单元分析结果按索引编号逐个装配到整体矩阵中,得到关于所有控制点变量的整体方程[20-22]:

式中:K为整体刚度矩阵;q为控制点位移列阵;P为控制点等效荷载列阵。
对边界条件进行处理,求解线性方程组,即可得到控制点变量,从而求得位移等未知变量。
3.4IGA算法实现根据以上分析,IGA与FEA最大的不同在于基函数的选择,主要体现在前处理与求解分析过程中。因此,等几何分析可基于成熟的有限元分析进行改进,应用于不同领域工程问题的求解,参照有限元分析过程,绘制基于NURBS的等几何分析算法实现步骤如图9所示。
(1)建模前处理。利用NURBS几何造型技术建立适合分析的几何模型(ASG)模型,结构相对简单的模型可通过NURBS工具箱建立,对于复杂的几何模型则可利用Rhinoceros等参数化建模软件生成,得到的几何模型由控制点和节点向量构成,自动生成初始单元网格;为提高求解精度,采用h、p、k三种策略细化单元网格,得到高密度、高精度、高阶的连续网格单元,并将控制点、基函数等关键信息传递给求解分析模块。
(2)计算求解。引入等参元思想,利用MATLAB提取分析模型的单元网格、NURBS基函数等信息,将待求解变量(如位移、温度等)表示为建模时应用的NURBS基函数与相关系数组合的形式,相关系数通常为控制顶点变量;通过数值积分等手段得到单元系数矩阵,遍历NURBS单元装配生成整体矩阵,施加边界条件后,求解整体控制方程,得到数值解。
(3)后处理分析。将控制顶点的计算结果在NURBS单元内直接采样,利用软件ParaView对结果进行后处理,若仿真结果精度满足要求,则输出仿真结果。若精度不满足要求,无需通过前处理调整ASG模型,直接对模型细化处理后求解即可,这一过程信息交互方便,克服了FEA信息的不足,实现了CAD/CAE的集成。
4 算例对比分析
4.1等几何模型建立以某水电站碾压混凝土重力坝为例进行等几何数值仿真分析,旨在通过此算例说明IGA在求解上的优势。某工程以发电为主,电站为一等工程,工程规模为大(1)型,工程枢纽主要由碾压混凝土重力坝、坝身泄洪表孔和泄洪放空底孔等泄洪建筑物以及左岸折线坝身进水口和地下引水发电系统组成,水库正常蓄水位1619 m,相应库容14.18亿m3,选取计算坝段高114 m,建立初始的多片等几何模型,如图10所示,每片模型至少包含一个单元。

图10 碾压混凝土重力坝等几何模型
坝体碾压混凝土材料参数:弹性模量28 GPa、泊松比0.167、密度2400 kg/m3;地基基岩材料参数:弹性模量22 GPa、泊松比0.25。利用k-细化策略对网格细化,得到分网方案一到方案五,5种方案每片模型网格数分别为:4、16、64、256、1024个。图11所示为方案二的网格模型。为便于对比研究,同时建立网格密度相同的有限元分析模型。模型建立完成后,确定模型的边界条件并施加如图12所示的静力荷载,包括:坝体自重、上游水压力、坝底扬压力、基岩的位移约束等。采用等几何分析(IGA)与有限元分析(FEA)两种方法对碾压混凝土重力坝进行求解分析,其中IGA方法采用2阶、3阶和4阶NURBS基函数求解,FEA则采用4节点平面单元(一次有限元)和8节点平面单元(二次有限元)进行求解分析。
4.2IGA与FEA数值仿真计算对比分析
4.2.1计算精度对比分析通过IGA与FEA的静力求解,得到如图13所示的碾压混凝土重力坝位移云图。从图13可以发现,等几何分析方法可以得到连续的物理场分布,坝体最大位移均出现在坝顶,IGA求解得到最大位移为1.029 cm,FEA计算得到最大位移为1.031 cm,两种方法计算得到结果接近,表明IGA结果可作为工程参考。
图11 方案二等几何网格模型

图12 加载示意图

图13 碾压混凝土重力坝位移云图(单位:m)
在相同荷载的作用下,改变单元密度,典型点位移与应力数值解随单元数增加的变化趋势分别如图14、图15所示,对比不同方法的计算结果可以得出以下结论:(1)无论是IGA方法还是FEA方法,随着网格密度的增加,典型点数值解的精度不断提高,并逐渐趋于稳定值,符合数值求解的一般规律;(2)对于IGA,选取基函数的阶次越高,低网格密度时数值解越接近于稳定值,收敛速度越快,即求解精度排序为:4阶IGA>3阶IGA>2阶IGA;(3)对于FEA,利用8节点平面单元(二次有限元)计算结果精度高于4节点平面单元(一次有限元)且收敛速度更快;(4)以收敛速度和计算精度为指标,将选用的数值分析方法按收敛速度排序为:4阶IGA>3阶IGA>2阶IGA≈2次FEA>1次FEA。
根据上述结果,选取2阶IGA、2次FEA和1次FEA的计算结果并得到图16所示的坝体水平截面应力分布。从图16可以看出,当网格密度较低时,因控制点或节点数量相对较少,出现明显的折线,数据离散性大;随着单元数的增加,水平截面的应力分布曲线逐渐趋于平滑,结果更加可靠。

图14 位移数值解随单元数的变化规律
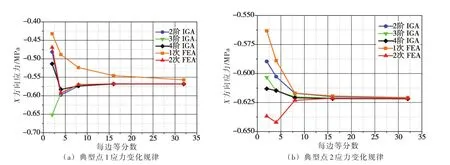
图15 应力数值解随单元数变化规律

图16 坝体水平截面应力分析结果
为充分比较IGA与FEA方法的计算精度,选取每边16等分和32等分的坝体截面应力分布,如图17所示。从图17可以看出,利用2阶IGA、2次FEA和1次FEA得到的坝体内部应力值接近,均能较准确地反映应力分布规律,但1次FEA得到的靠近坝体边缘位置应力分布发生转折,结果明显失真;2阶IGA与2次FEA得到的整个截面应力分布一致性较高。因此,综合比较IGA与FEA数值解的收敛速度与计算精度,IGA计算结果整体上优于FEA,其中2阶IGA与2次FEA结果较为接近,二者均优于1次FEA,计算精度排序为:4阶IGA>3阶IGA>2阶IGA≈2次FEA>1次FEA。

图17 坝体水平截面应力分析结果
4.2.2求解效率对比分析根据上述分析可知,2阶IGA与2次FEA数值解的收敛速度和求解精度较为接近,本节主要对两类方法的求解效率进行分析。无论是IGA还是FEA,分析模型的自由度数直接影响仿真计算的成本和时间,自由度数的大幅增加必然会造成求解时间的增加和计算资源的不合理分配,因此,模型的自由度数能够直接衡量数值分析方法的求解效率。表2为2阶IGA、2次FEA和1次FEA采用分析模型的单元个数与自由度数。

表2 分析模型的单元个数与自由度数
图18为分析模型自由度数随网格密度的变化规律。从图18可以看出,随着单元数的增加,自由度数不断上升,在3种选用的计算模型中,2次FEA自由度数上升速度最快,求解效率较低;相比之下,2阶IGA与1次FEA计算自由度上升速度均较慢,求解效率相对较高,三者求解效率排序为:2次FEA>2阶IGA≈1次FEA。综合考虑计算精度与求解效率,2阶IGA的计算精度和收敛速度高于1次FEA且与2次FEA接近,利用2次FEA模型求解时,自由度较高,求解时间较长、效率较低。综合以上分析,2阶IGA不但具有计算精度高和数值解收敛速度快的特点,在模型求解效率方面也表现出优良特性。因此,IGA相比FEA在计算方面体现出较大的优势。

图18 自由度数随网格密度的变化规律
5 结论
本文以传统有限元方法为参照,实现了等几何分析算法的建模、计算求解与分析,将等几何分析方法应用于碾压混凝土重力坝的应力数值分析,通过IGA与FEA的仿真计算结果对比,表明IGA在模型建立与求解计算两方面优势明显:(1)等几何分析方法统一了有限元分析中几何模型与分析模型,消除了二者的差异,实现了CAD/CAE的集成;(2)适用于等几何方法的分析模型具有几何精确性,无需二次建模分网的过程节省了仿真分析时间,且单元间保持高阶连续,网格细化时仍然保持对几何特征的精确表达;(3)等几何方法的数值解收敛速度快、计算精度高,其中2阶IGA数值解的精度优于普遍采用的1次FEA,与2次FEA接近;(4)等几何方法的求解效率高、仿真成本小,对于计算精度接近的2阶IGA与2次FEA,2阶IGA计算自由度数较少,效率更高。
等几何分析方法已在多个工程领域应用的过程中表现出优良的特性,考虑其建模与求解的优势,该方法有望解决考虑复杂地形地质条件下的大型水工结构三维建模与计算难以有效耦合的问题,实现跨尺度建模、精细化分析,以及取代有限元分析应用于水利工程中温度场、渗流场、动力分析和水力学等问题的求解分析。因此,对于等几何分析方法在复杂结构建模与高效计算分析方面还需不断深入研究。
参考文献:
[1]汪洋,贾金生,冯炜,等 .考虑高压水劈裂的高重力坝安全性试验研究[J].水利学报,2016,47(11):1397-1404.
[2]张社荣,王高辉.混凝土重力坝抗爆性能及抗爆措施研究[J].水利学报,2012,43(10):1202-1213.
[3]张冲,王仁坤,汤雪娟.溪洛渡特高拱坝蓄水初期工作状态评价[J].水利学报,2016,47(1):85-93.
[4]李明超,张梦溪,王孜越.考虑诱导缝的碾压混凝土重力坝控裂结构温度场与温度应力数值分析[J].水利学报,2017,48(5):551-559,567.
[5]KAGAN P,FISCHER A,BAR-YOSEPH P Z.New B-Spline Finite Element approach for geometrical design and mechanical analysis[J].International Journal for Numerical Methods in Engineering,1998,41(3):435-458.
[6]BAZILEVS Y,CALO V M,COTTRELL J A,et al.Isogeometric analysis using T-splines[J].Computer Methods in Applied Mechanics and Engineering,2010,199(5):229-263.
[7]HUGHES T J R,COTTRELL J A,BAZILEVS Y.Isogeometric analysis:CAD,finite elements,NURBS,exact geometry and mesh refinement[J].Computer Methods in Applied Mechanics&Engineering,2005,194(39/41):4135-4195.
[8]徐岗,王毅刚,胡维华.等几何分析中的r-p型细化方法[J].计算机辅助设计与图形学学报,2011,23(12):2019-2024.
[9]祝雪峰.复杂曲面非协调等几何分析及相关造型方法[D].大连:大连理工大学,2012.
[10]AURICCHIO F,CALABRO F,HUGHES T J R,et al.A simple algorithm for obtaining nearly optimal quadrature rules for NURBS-based isogeometric analysis[J].Computer Methods in Applied Mechanics and Engineering,2012,249/252(2):15-27.
[11]WANG D,XUAN J.An improved NURBS-based isogeometric analysis with enhanced treatment of essential boundary conditions[J].Computer Methods in Applied Mechanics and Engineering,2010,199(37):2425-2436.
[12]陈涛,莫蓉,万能,等 .等几何分析中采用Nitsche法施加位移边界条件[J].力学学报,2012,44(2):369-381.
[13]deFALCO C,REALI A,VÁZQUEZ R.GeoPDEs:a research tool for isogeometric analysis of PDEs[J].Advances in Engineering Software,2011,42(12):1020-1034.
[14]NGUYEN V P,ANITESCU C,BORDAS S P A,et al.Isogeometric analysis:an overview and computer implementation aspects[J].Mathematics and Computers in Simulation,2015,117:89-116.
[15]尹硕辉,余天堂.等几何分析与有限元直接耦合法[J].计算机辅助工程,2014,23(2):31-36.
[16]张勇,林皋,胡志强,等 .基于等几何分析的比例边界有限元方法[J].计算力学学报,2012,29(3):433-438.
[17]TEMIZER I,WRIGGERS P,HUGHES T J R.Contact treatment in isogeometric analysis with NURBS[J].Computer Methods in Applied Mechanics and Engineering,2011,200(9):1100-1112.
[18]BAZILEVS Y,CALO V M,HUGHES T J R,et al.Isogeometric fluid-structure interaction:theory,algorithms,and computations[J].Computational Mechanics,2008,43(1):3-37.
[19]WALL W A,FRENZEL M A,CYRON C.Isogeometric structural shape optimization[J].Computer Methods in Applied Mechanics and Engineering,2008,197(33):2976-2988.
[20]张勇.等几何分析方法和比例边界等几何分析方法的研究及其工程应用[D].大连:大连理工大学,2013.
[21]ZHONG D,LI M,SONG L,et al.Enhanced NURBS modeling and visualization for large 3D geoengineering applications :An example from the Jinping first level hydropower engineering project,China[J].Computers&Geosciences,2006,32(9):1270-1282.
[22]曾攀.有限元分析及应用[M].北京:清华大学出版社,2004.
[23]BRINO M.CAD-CAE integration and isogeometric analysis:trivariate multipatch and applications[D].Politecnico di Torino,2015.
[24]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.

