群体简单宣告逻辑*,†

徐康

浙江水利水电学院 社科部xukanguuu@163.com

王轶‡

浙江大学 哲学系、语言与认知研究中心ynw@xixilogic.org

1 引言

公开宣告逻辑（[13]）在经典认知逻辑（[8,6,12]）的基础上扩充以表达公开宣告的算子，是最简单的动态认知逻辑之一。任意公开宣告逻辑（[2]）在此基础上添加任意公开宣告算子，从而允许使用诸如“在某个公开宣告后知道φ”的语句；这样的语句可以简单理解为“φ（通过宣告）可知”。群体宣告逻辑（[1]）则关注不同主体的宣告所带来的动态变化。公式〈G〉Kiφ表示“群体G中的主体可以同时做出某种公开宣告，以使得主体i知道φ”；这也是一种“φ可知”语句，只不过知识的获取仅能经由群体同时宣告实现。任意公开宣告逻辑并不能归约为群体宣告逻辑；反过来，群体宣告逻辑是否可以归约为任意公开宣告逻辑，则仍然是一个悬而未决的问题。

群体宣告逻辑的常用例子是诸如泥孩难题、俄罗斯卡牌问题（[5,第4.12节]）等需要对群体同时宣告前后情况变化进行推理的问题。这些例子中宣告的内容既可以是一阶知识（即对事实的认识），比如甲宣告自己知道头上有泥巴；也可以是高阶知识，比如甲宣告自己知道乙知道甲手上的卡牌。如果仅从解答问题的角度考虑，这些例子中允许宣告高阶知识无可厚非，甚至从协议1俄罗斯卡牌问题中要求甲和乙进行公开的信息传递并使丙无法获知实际信息（甲和乙手上是哪些卡牌），其解答可被视为构建一个信息传递协议。的安全性角度考虑，使用高阶知识似乎更易被接受。

然而现实情况下很多时候并不接受宣告高阶知识。例如，当评审委员会审议到底录用哪位应聘者时，各位评委通常只能针对应聘者的情况给出事实性的宣告，这样的宣告常常体现在该评委说出“我认为（或不认为）这位候选人……”这样的话；一位评委通常很少采用“我认为另一位评委认为（或不认为）……”这样的表述，否则这位评委的话容易给旁听者以不客观或有其它所指等印象。人类务实交流过程中通常追求简单明确，而允许宣告高阶知识的场合，很多时候与智力游戏或是特定领域的深入探索等有关。

基于上述考虑，本文引入群体简单宣告逻辑。公式〈G〉Kiφ表示“群体G中的每个主体可以同时公开宣告某个一阶知识，以使主体i知道φ”，亦即“φ通过群体一阶知识宣告可知”。群体简单宣告逻辑在很多地方与群体宣告逻辑相似，但也不尽然；最突出的差别有两点。一是在群体宣告逻辑中，有穷规则R[G]不可靠，其已知的公理系统使用了基于容许型的无穷规则；而类似的有穷规则在群体简单宣告逻辑中保持有效性，从而使其公理系统更美观。二是公式〈G〉〈H〉φ→〈G∪H〉φ，可直观解读为“多群依次宣告可由一次宣告实现”；该公式在群体宣告逻辑中有效，但在群体简单宣告逻辑中却不是有效式。

本文将对群体简单宣告逻辑的表达能力和公理系统进行探讨。首先对群体简单宣告逻辑的有效式和归约式进行梳理。在表达能力方面，主要与公开宣告逻辑进行对比。公理系统以及完全性定理的证明基本采用[2]中的方法，但在完全性证明中本文改为使用经典的“理论”定义，从而适度简化证明过程。顺便一提，[4,3]宣称提供了任意公开宣告逻辑完全性的更简单证明方法，但简化程度有待商榷。

论文结构安排如下：第2节简要介绍经典认知逻辑、公开宣告逻辑和群体宣告逻辑等基础理论。第3节证明[2]中提出的有穷规则是不可靠的。第4节引入群体简单宣告逻辑，之后的第5和第6两节分别探讨群体简单宣告逻辑的表达能力和公理系统。第7节进行总结。

2 背景

本节简要介绍经典认知逻辑、公开宣告逻辑和群体宣告逻辑，这些内容都是论文主体部分的所依赖的背景知识。

本文设定pr是可数非空的命题变元集，ag是一个有穷非空的主体集合，gr是所有群体的集合，即gr=℘(ag)；在此设定下可考虑空群，记为∅。

2.1 认知逻辑（EL）和公开宣告逻辑（PAL）

在命题逻辑（简称PL）基础上增加刻画“知道”的模态算子可以得到经典认知逻辑（[8,6,12]，简称EL）。公开宣告逻辑（[13]，简称PAL）在经典认知逻辑基础上进一步增加对公开宣告的刻画，是最简单的动态认知逻辑之一。本节简要介绍经典认知逻辑和公开宣告逻辑以方便后文的叙述，对这两类逻辑的更详细介绍参见[5]。

上述三个逻辑的语言由如下语法规则分别给出（其中p∈pr且i∈ag）：

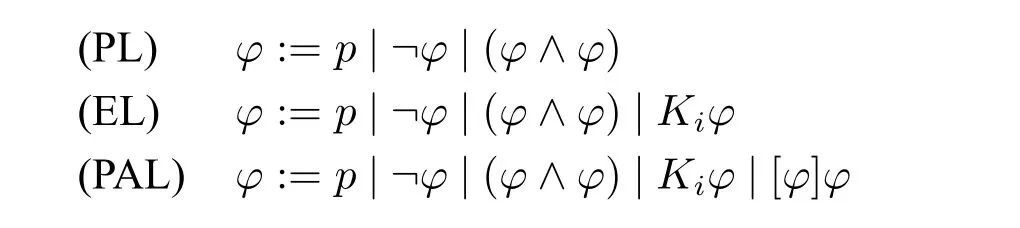
Ki的对偶算子记为形式上将视为¬Ki¬φ的缩写。类似地，[φ]的对偶算子为 〈φ〉，并且 〈φ〉ψ 视为 ¬[φ]¬ψ 的缩写。

公式[φ]ψ可以直观理解为“公开宣告φ之后，ψ成立”。而〈φ〉ψ可以理解为“并非在公开宣告φ之后，¬ψ成立”，亦即“公开宣告φ，且此后ψ成立”。通常使用面向认知解释的可能世界模型来给出PAL的形式语义。三元组M=(W,～,V)称为知识模型（简称模型、亦称S5模型），如果满足：

·W是非空集合，其中元素称为可能世界、状态或点；

对于所有s∈W，称(M,s)为知识状态；简单起见，外层括号常被省略。PAL的形式语义给出如下。令p∈pr，i∈ag，(M,s)=((W,～,V),s)为知识状态，满足关系（符号|=PAL）由如下条件给出：

M,s|=PALp 当且仅当 s∈V(p)

M,s|=PAL¬φ 当且仅当 并非M,s|=PALφ

M,s|=PAL(φ∧ψ) 当且仅当 M,s|=PALφ且M,s|=PALψ

M,s|=PALKiφ 当且仅当 对所有t，如果s～it，则M,t|=PALφ

M,s|=PAL[φ]ψ 当且仅当 如果M,s|=PALφ，则M|φ,s|=PALψ

其中M|φ=(W′,～′,V′)是M 的子模型，满足：

·W′={s′∈ W|M,s′|=PALφ}；

·～′∶ag → ℘(W′×W′)使得对任意

·V′(p)=V(p)∩ W′。

称PAL公式φ（在PAL中）有效，当且仅当对所有知识状态(M,s)，M,s|=PALφ。下列公式是PAL的有效式：

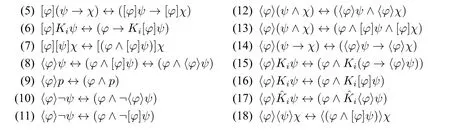
PAL与EL的表达能力相同。图1中展示EL公理系统S5，以及在S5的基础上增加归约公理而得到的PAL公理系统PAL。（[13,9,10]）

图1:公开宣告逻辑的公理系统PAL，其子系统S5由(PC),(K),(T),(5),(MP)和(N)组成。去掉宣告规则（RA）所得到的系统并不会丢失任何定理，但对于公开宣告逻辑的某些扩张（例如带公共知识的公开宣告逻辑）这条规则可能无法省略，因此为避免遗失，这里统一添加上。4公理（即Kiφ→KiKiφ，正自省公理）常常也被包含在上述系统中，但它可由S5推演得到。

2.2 群体宣告逻辑（GAL）

群体宣告逻辑（[1]，简称GAL）以公开宣告逻辑为基础，关注公开宣告的群体行为。群体宣告逻辑的语言是对公开宣告逻辑语言的真扩张，增加一组群体宣告算子[G]（G∈gr）。具体定义如下：

定义2.1(语言L) 群体宣告逻辑的语言L由如下规则给出（其中p∈pr，i∈ag且G∈gr）：

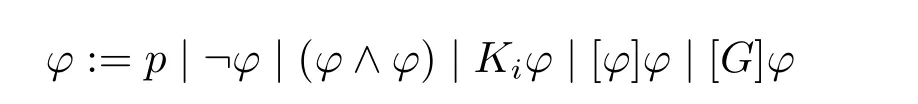
L采用跟 PAL语言一样的设定，此外 [G]的对偶算子记为 〈G〉，即 〈G〉φ视为¬[G]¬φ的缩写。当G是某个单点集{i}时，一般将算子[{i}]和〈{i}〉分别简写为 [i]和 〈i〉。类似地，算子[ij]和 〈ij〉分别是 [{i,j}]和 〈{i,j}〉的缩写。

直观上来讲，[G]φ将被用于表示“G中主体同时做出任意宣告，φ都成立”，〈G〉φ则表示“G中主体同时做出的某个宣告能使得φ成立”。GAL中要求每次群体宣告的内容满足：(1)必须是真实知识，即每个主体所宣告的内容都是该主体的知识；(2)必须是公开的，即在群体宣告发生后所有主体都能够获取该群体宣告的信息；(3)群体中的所有主体同时做出宣告（多次群体宣告中的每次宣告都需要满足此要求，但不同批次的宣告具有先后性）。

假设p∈pr、i∈ag、G∈gr且(M,s)是知识状态，则群体宣告逻辑的语义满足关系（符号|=GAL）在PAL语义的基础上增加如下归纳条件：

相对于公开宣告逻辑，[1]中提供了群体宣告逻辑中如下一些额外的有效式（其中p∈pr、i,j∈ag、G,H ∈gr且φ是任意GAL公式）：

(1)群体宣告不改变原子命题的真值：

(2) 〈i〉Kjp ↔ 〈j〉Kip

(3) 空群宣告退化为未宣告：〈∅〉φ ↔ [∅]φ 和 [∅]φ ↔ φ

(4)群体宣告全称消去和存在引入（其中ψi是EL公式）：

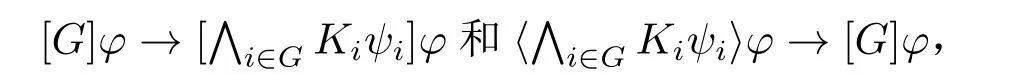
(5)平凡宣告退化为未宣告：[G]φ→φ和φ→〈G〉φ

(6)同群多次宣告可由一次宣告实现：[G]φ→[G][G]φ和〈G〉〈G〉φ→〈G〉φ

(+) 由 (5)和 (6)可得到 [G]φ ↔ [G][G]φ 和 〈G〉φ ↔ 〈G〉〈G〉φ

(7)多群依次宣告可由一次宣告实现（不确定蕴涵反方向是否有效）：

(8)Church-Rosser公式：〈G〉[G]φ → [G]〈G〉φ（不确定蕴涵反方向是否有效）

(9)广义Church-Rosser公式：〈G〉[H]φ → [H]〈G〉φ（蕴涵反方向不有效）

(10)“必然会知道”当且仅当“知道必然会”：

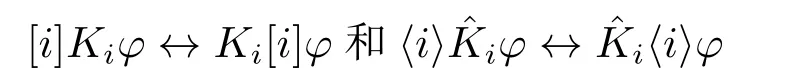
(11)“知道如何做”就“知道能做”：

(12)“知道如何做”当且仅当“知道知道如何做”：

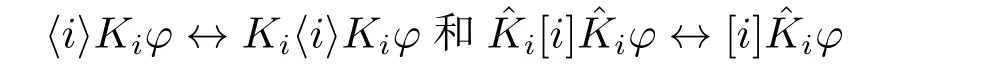
2.2.1 群体宣告逻辑的公理系统

在介绍群体宣告逻辑的公理系统之前首先引入如下定义。

定义2.2(容许型；Goldblatt[7,p.55]) 容许型由如下语法规则给出：

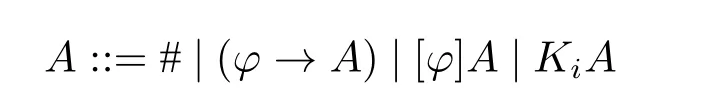
其中#是给定符号，φ是GAL公式，且i∈ag。

如果A是容许型，那么A(φ)表示用φ替换A中#后得到的公式。不难发现，任给公式φ和容许型A，A(φ)是GAL公式。

[1]中提供了GAL的一个可靠且完全的公理系统，它包含PAL的所有公理和规则以及以下三条公理或规则：

(1)[G]φ → [∧i∈GKiψi]φ，其中所有 ψi是 EL 公式；

(2)由φ得到[G]φ；

(3) 由 A([∧i∈GKiαi]φ)得到 A([G]φ)，其中所有 αi都是 EL 公式。

[1]中将上述第(3)条规则称为Rω([G])，其中的上标“ω”直观上表明该条规则本身代表了可数无穷多种形式，这样的规则有时被称为无穷规则（infinitary rule）。[1]中还曾给出另一规则R[G]：

·由 φ → [χ][∧i∈GKipi]ψ 得到 φ → [χ][G]ψ，其中所有pi都不在 φ、ψ 和 χ中出现。

规则R[G]被称为有穷规则（finitary rule）2这里称其为有穷规则并不意味着该公理系统是有穷的公理系统；后者要求公理系统只使用有穷多条公理，以具备更美观的数学形式。本文的公理系统通过公理模式给出，并不是有穷的公理系统；此类系统如果要转变为有穷系统，通常可以使用代入规则实现。然而公理AP导致代入规则不可靠，因此无法简单地转变为有穷的公理系统，甚至很有可能不是有穷可公理化的。。[1]中试图证明将无穷规则Rω([G])替换为有穷规则R([G])后得到的公理系统与原系统等价，并因此也是GAL的具有可靠性与完全性的公理系统。然而这一证明中存在错误（文中Lemma 16无法得到），使用有穷规则的系统并不可靠，下节中证明其不可靠性。

3 有穷规则不是可靠的群体宣告逻辑规则

第2.2.1节中提到，[1]中提出使用有穷规则R[G]的公理系统，即包含PAL的所有公理和规则外加以下三条公理或规则的公理系统：

·[G]φ → [∧i∈GKiψi]φ，其中所有 ψi是 EL 公式；

·由φ得到[G]φ；

·规则R[G]：由 φ → [χ][∧i∈GKipi]ψ 得到 φ → [χ][G]ψ，其中所有pi都不在

φ、ψ和χ中出现。

然而该公理系统不是群体宣告逻辑的可靠系统。本节证明，R[G]不是群体宣告逻辑的可靠规则，即：

定理1在GAL中，规则R[G]不保持有效性。

下面给出定理1具体证明。只需找到具体反例，使得规则的前提有效但结论不有效。准确说来，在规则R[G]中取：

引理1

证明:假设存在知识状态(M,s)不满足该公式，则如下两项成立：

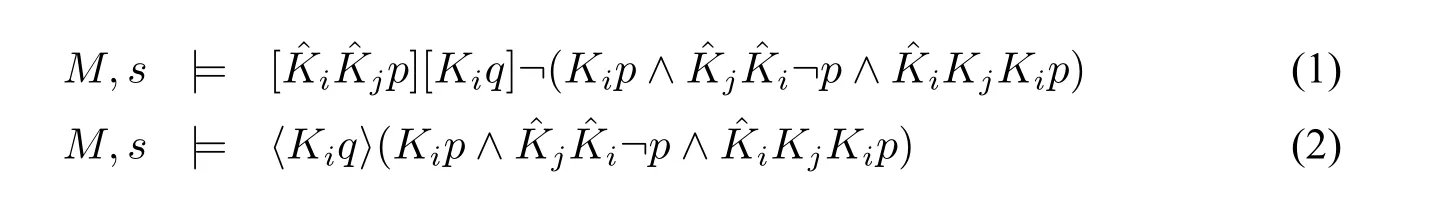
由M|Kiq,s|=Kip知M|Kiq,s|=p，则M,s|=p，并因此由（缩小模型不会减少一阶知识，这一结论将在下面反复使用）。再由(1)知则有：

由M,s|=Kiq知对所有t～is，有M,t|=Kiq，即t∈ M|Kiq。因M|Kiq,s|=Kip，对所有t～is，有M|Kiq,t|=p，故M,t|=p，因此有M,s|=Kip，所以：

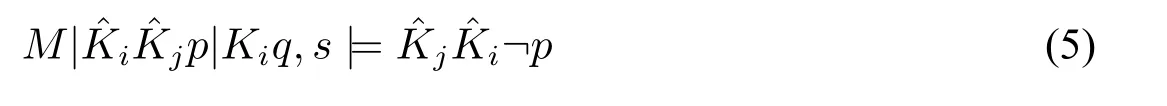
接下来证明u2M|Kiq。假设u2∈M|Kiq。由u1∈M|Kiq且M|Kiq,u1|=KjKip（见u1引入处）知对所有u4∈M|Kiq使得u1～ju4，都有M|Kiq,u4|=Kip；同理M|Kiq,u2|=Kip（据本段假设及u1～ju2）。因此矛盾。

根据u2M|Kiq知存在u5∈M使得u2～iu5且M,u5|=¬q。由u1～ju2、u2～iu5和M,u1|=p可得因此且矛盾。因此假设不成立，引理得证。□

引理2

证明:需找到一个知识状态(M,s)，使得定义知识模型M=(W,～,V)满足如下条件：

·W={s,t1,t2,t3,t4,t5,t6,t7}；

·～使得：～i是二元关系{(s,t4),(t1,t2),(t5,t6)}的自反对称传递闭包，～j是{(s,t1),(t2,t3),(t4,t5),(t6,t7)}的自反对称传递闭包，且对任意不同于i和j的主体k，都有～k=∅；

·V使得：V(p)={s,t4}，V(r)={t3}，且对任意q∈pr{p,r}，V(q)=∅。M的直观如下图所示（其中在状态的上标中明确标注的命题在该状态中为真，其它未标注的命题在该状态中皆为假）：

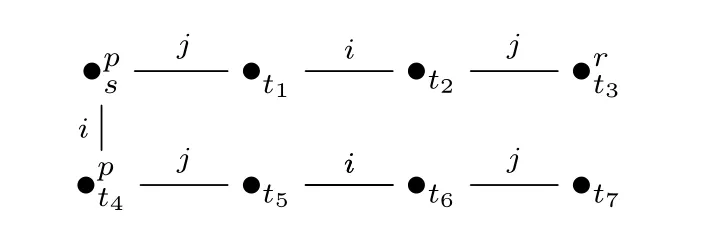
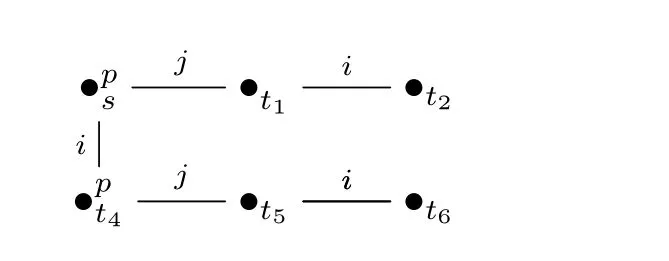
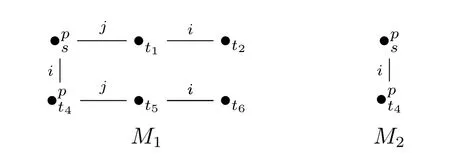
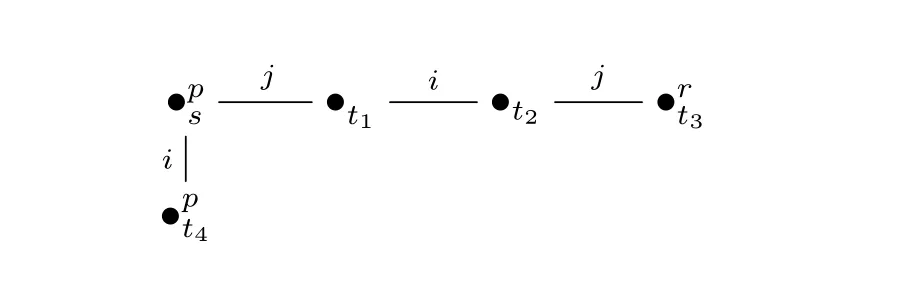
需要指出的是，[11]为APAL公理系统中的有穷规则找出的反例对于本节证明中反例的寻找有帮助。这里反例的复杂程度更高一些。

4 群体简单宣告逻辑

在第2.2节给出的群体宣告逻辑（GAL）中，算子[G]的语义要求宣告内容为EL公式。但正如引言中所提到的那样，在实际中，理性主体的宣告往往只是用于陈述事实的一阶知识，本节将引入新的逻辑以刻画这类问题。

群体简单宣告逻辑（Group Simple Announcement Logic，简称GSAL）是在群体宣告逻辑的基础上，规定群体宣告的内容只能是基于命题公式的一阶知识而得到的逻辑系统。

GSAL使用与GAL完全一样的语言，即语言L（定义2.1）。本文从现在开始以L为默认语言，除明确指定，“公式”即指语言L中的公式。

GSAL的语义与GAL稍有不同。群体G中主体宣告的内容必须是真实的、公开的，且由G中的主体同时做出宣告。但是宣告内容有所不同，GSAL要求宣告的是命题逻辑的公式，这可以从如下语义解释中看到。

定义4.1(满足) 假设p∈pr、i∈ag、G∈gr且(M,s)是知识状态，则群体简单宣告逻辑的语义满足关系（符号|=）由如下归纳条件给出：

其中M|φ的定义参考PAL语义。称公式φ（在GSAL中）有效，记为|=GSALφ或简单写成|=φ，当且仅当对所有知识状态(M,s)，M,s|=φ。

根据上述定义，对于[G]的对偶算子〈G〉，不难发现M,s|=〈G〉φ当且仅当存在 PL 公式集 {αi|i∈ G} 使得 M,s|= 〈∧i∈GKiαi〉φ。

类似于GAL，在GSAL中[G]φ直观上仍被用于表示“G中主体同时做出任意宣告，φ都成立”，只不过这里将群体宣告的内容限制为PL公式而GAL中允许EL公式，也就是说GSAL中群体任意宣告的内容不能是高阶知识，比如“别人知道某某事情”。3某个主体i宣告α实际起到的效果是Kiα被宣告，即“我知道α”。因此根据所知皆真和正内省定理（可以得到|=Kiα↔KiKiα），群体任意宣告的内容实际上可以是“我知道我知道α”这样的自指高阶知识。

在EL、PAL和GAL中互模拟都对公式的满足关系封闭，GSAL中也是如此，即如下命题成立：

命题4.1(互模拟性质) 任给认知状态(M,s)和(M′,s′)，任给公式φ，如果(M,s)和(M′,s′)互模拟，则M,s|=φ当且仅当M′,s′|=φ。

GAL的有效式多数仍然是GSAL的有效式：

命题4.2令p∈pr、i,j∈ag、G,H∈gr且φ是任意公式，则下列公式都是有效式（证明从略）：

(1)p→ [G]p、¬p→ [G]¬p、〈G〉p→ p和 〈G〉¬p → ¬p

(2) 〈i〉Kjp ↔ 〈j〉Kip

(3) 〈∅〉φ ↔ [∅]φ 和 [∅]φ ↔ φ

(4)[G]φ → [∧i∈GKiαi]φ 和 〈∧i∈GKiαi〉φ → [G]φ，其中 αi都是 PL 公式

(5)[G]φ → φ 和 φ → 〈G〉φ

(6)[G]φ → [G][G]φ 和 〈G〉〈G〉φ → 〈G〉φ

(+) 由 (5)和 (6)可得到 [G]φ ↔ [G][G]φ 和 〈G〉φ ↔ 〈G〉〈G〉φ

(7) 〈G〉[G]φ → [G]〈G〉φ（不确定蕴涵反方向是否有效）

(8) 〈G〉[H]φ → [H]〈G〉φ（蕴涵反方向不有效）

不难发现，GSAL的有效式有两条与GAL不同：

2.GAL中有一条有效式：[G∪H]φ→[G][H]φ，而这不是GSAL的有效式（参见定理2）。

定理2假设G,H∈gr，则：

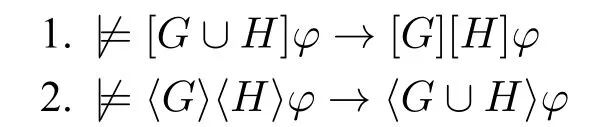
证明:定理1、2两项等价，这里证明第2项。考虑满足如下条件的知识模型M=(W,～,V)：

·W={s,t,u,v}；

·～使得：～i为{(s,t),(u,v)}的自反对称传递闭包，～j为{(s,u),(s,v)}的自反对称传递闭包，且对任意k∈gr{i,j}，～k=∅；

·V使得：V(p)={s}，V(q)={s,t,u}，且对任意r∈pr{p,q}，V(r)=∅。模型M的直观形式可以下图(1)表示：

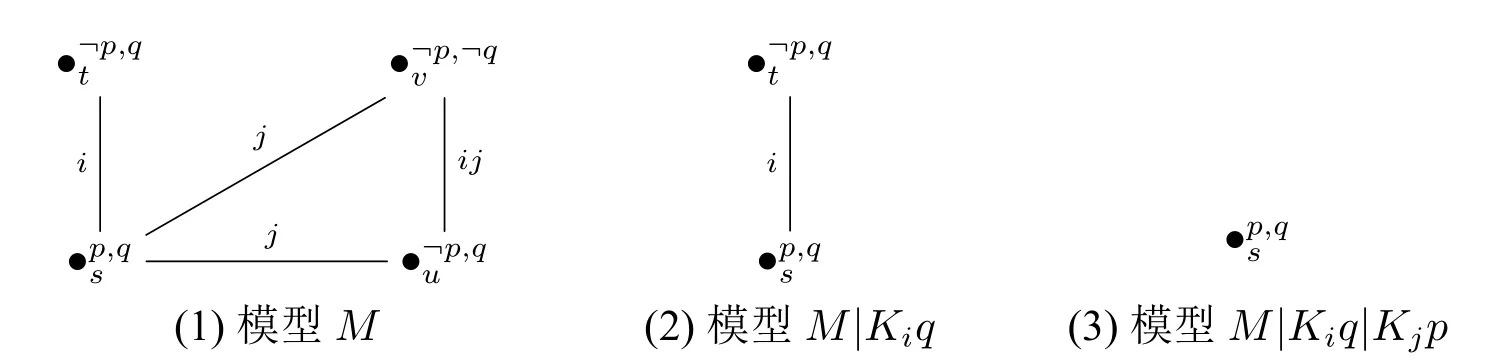
根据语义定义，M,s|=〈ij〉Kip当且仅当存在PL公式α和β使得M,s|=〈Kiα ∧Kjβ〉Kip，当且仅当存在 PL公式 α 和 β 使得 M,s|=Kiα ∧Kjβ 且M|(Kiα∧Kjβ),s|=Kip。要使M,s|=Kiα∧Kjβ，必须有α在s和t上真，且β在s、u和v上都真。又因为t和u的赋值完全相同，因此α和β在两个世界上同真同假，即有如下情况：

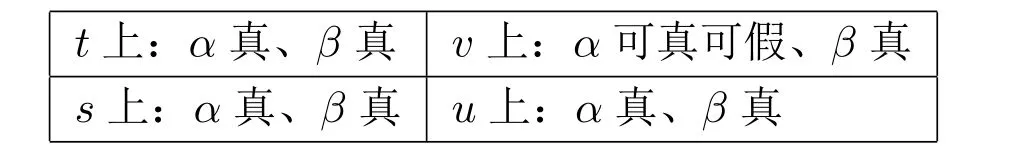
因此，模型M|(Kiα∧Kjβ)或者等同于M本身，或者等同于M|Kiq；在两种情况下Kip都为假。即M,s|=Kiα ∧Kjβ 不成立，因此M,s〈ij〉Kip。

除了上面所提到的以外，还可以发现一些额外的有效式：

命题4.3(群体宣告归约性质) 假设φ和ψ是公式且α是PL公式，则下列公式是有效式：

1.[G](φ ∧ ψ)↔ ([G]φ ∧ [G]ψ)

2.[G]φ → φ

3.[G]¬α ↔ ¬[G]α

4.[G]α ↔ α

5 表达能力

本节主要证明GSAL的表达能力严格强于PAL。假设语言L和L′是通过同一模型类进行解释的两个逻辑语言，称：

·L′至少与L有相同的表达力，记为LL′，当且仅当对于所有的L公式φ，都存在L′公式ψ，使得φ和ψ在同一模型的同一状态上的取值相同；

·L与L′有相同的表达力，记为L≡L′，当且仅当LL′且L′L；

·L′比L表达力强，记为L≺L′，当且仅当LL′且L̸L′；

·L和L′不可比较，当且仅当LL′且L′L。已经知道的结论有（参见[5,1]）：

·如果|ag|=1（语言中只有一个主体），那么PAL≡GAL；

·如果|ag|≥2，那么PAL≺GAL。

定理3如果|ag|=1，那么PAL≡GSAL。

证明:在|ag|=1的情况下，|=[i]φ↔φ，因此PAL≡GSAL。 □

定理4如果|ag|≥2，那么PAL≺GSAL。

证明:PALGSAL显然成立。要证明PALGSAL，需要证明存在GSAL公式φ，但找不到PAL（或EL）公式ψ 使得|= φ ↔ ψ。令φ = 〈{a,b,c}〉〈Kip∧¬KjKip〉。假设存在EL公式ψ使得|=φ↔ψ，令q和r是不在ψ中出现的命题变元，不难定义如下图所示的模型M和M′:

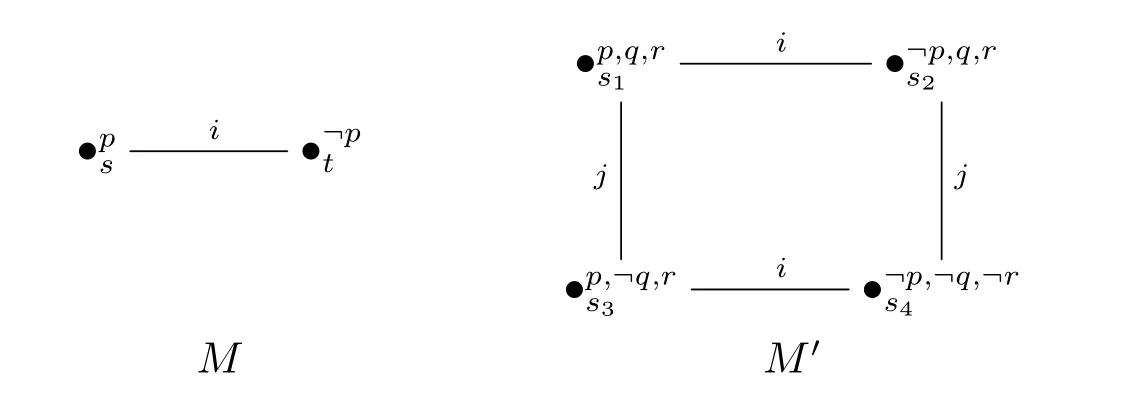
6 公理系统

群体简单宣告逻辑的公理系统GSAL如图2所示。GSAL包括PAL的所有

图2:群体简单宣告逻辑的公理系统GSAL

公理和规则以及以下三条公理或规则：

·AG：群体宣告化简公理（Axiom of Group Announcement Simplification）

·RG1：群体宣告引入规则（Rule of Group Announcement Introduction）

·RG2：群体宣告归纳规则（Rule of Group Announcement Induction）

GSAL是PAL的扩张，包含PAL的所有公理和规则。GSAL没有关于算子[G]的可归约的公理，这与语义情况一致。

6.1 等值置换规则

等值置换规则是非常重要但常被疏忽的一条规则。很多公理系统中无此规则，但该规则可容许，而有些系统中不容许此规则。在后一种情况下，一旦证明中用到此规则就可能得到错误结论。本节中将对此规则加以探讨。

所谓等值置换规则，是指由(ψ↔χ)得到(φ↔φ′)，其中φ′是将φ中的某个ψ替换为χ后得到的公式。

上述规则可以分别从语义和语法两个角度来看。对GSAL而言，从语义方面来看，下面的定理说明等值置换规则保持语义有效性。

定理5等值置换规则在GSAL中保持语义有效性。即任给公式ψ和χ使得|=ψ↔χ，任给公式φ。以φ′表示将φ中某个子公式ψ替换为χ后得到的公式，则|=φ↔φ′。

从语法方面看，则是说在公理系统中该规则可容许，亦即如下性质：

“任给公式ψ和χ使得⊢ψ↔χ，任给公式φ，并以φ′表示将φ中某个子公式ψ替换为χ后得到的公式，则⊢φ↔φ′。”

GSAL中并未明确允许使用等值置换规则，如果要用，则需要首先证明上述性质成立。然而要证明这一点存在一定的困难。事实上，对上述性质使用归纳证明（施归纳于φ的结构）时，当φ形如p、¬λ、(λ∧δ)、Kiλ、[G]λ时都可以得到证明，唯独[λ]δ情形存在问题，对此情形需要分别证明（其中λ′和δ′分别是将λ和δ中某个子公式ψ替换为与之等值的χ后得到的公式）：

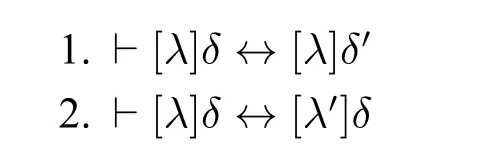
上述结论1也很容易证明，这里无法提供结论2的证明。

当然，根据定理5和下面将要证明的完全性定理，不难发现等值置换规则确实是GSAL可容许的规则。只是这样一来，在完全性定理的整个证明中必须保证不使用该规则，否则将陷入循环证明。

6.2 连续宣告

连续进行多次宣告有一些有意思的结论，而这些结论有些在某篇论文的某个证明用到，有些则从未被证明。本节将尝试对连续宣告进行系统化的梳理，一来便于读者查阅相关结论，二来也有助于下面的证明。

定理6(方形连续宣告) 任给自然数n（n≥1），命题变元p，公式ψ、χ和公式序列φ1,...,φn，如下公式是GSAL的定理：

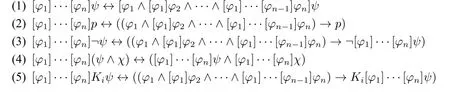
定理7(菱形连续宣告) 任给自然数n（n≥1），命题变元p，公式ψ、χ和公式序列φ1,...,φn，如下公式是GSAL的定理：

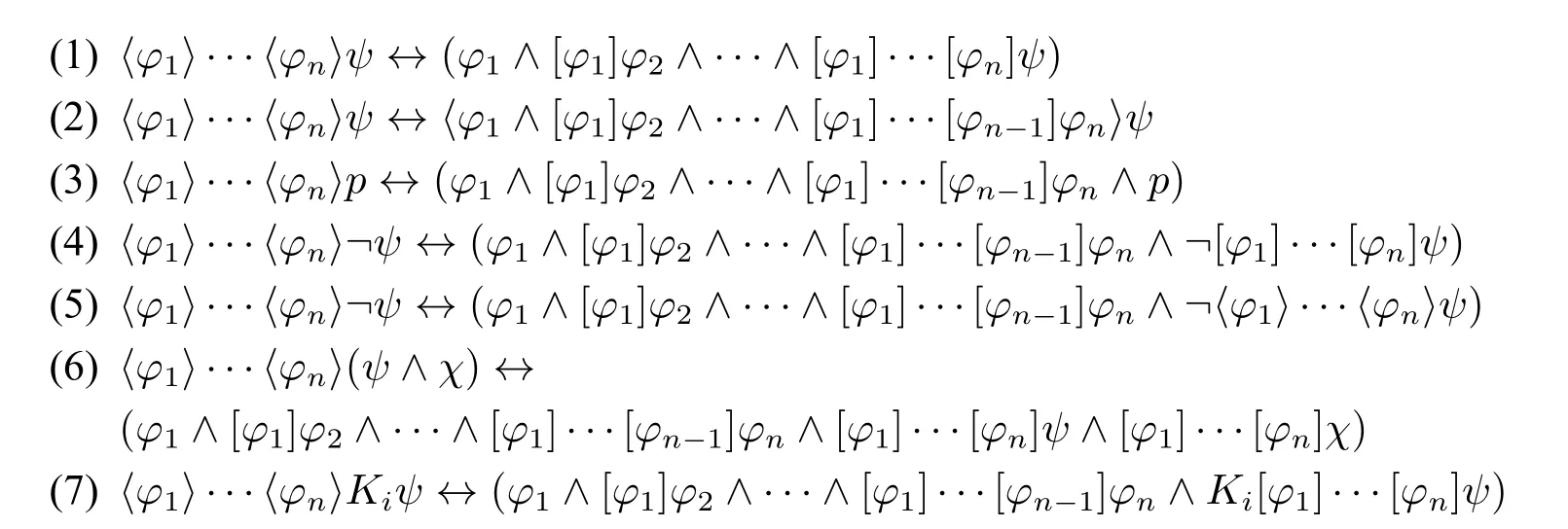
6.3 与GSAL证明能力相同的公理系统

本节中将引入两个与GSAL证明能力相同的两个公理系统：GSAL′和GSAL′′（图3），其目的是便于后文中完全性定理的证明。这两个公理系统与GSAL的差

图3:群体简单宣告逻辑的公理系统GSAL′和GSAL′′

上面定义的公式复杂度有时也称为模态度（modaldegree）。每条公式的复杂度都是一个自然数。所有PL公式的复杂度都为0，且[G]ψ的复杂度高于∧i∈GKiαi（其中αi是PL公式）。

引理3令Q={q1,...,qn,...}为一集命题变元，Γ={α1,...,αk}是一集PL公式，使得Γ中出现的命题变元与Q中的命题变元不相交。对任意GSAL公式别在于将规则RG2分别替换为RG2′和RG2′′（其中A是定义2.2中引入的容许型概念的GSAL版本）：

·RG2′：由 A([∧i∈GKipi]φ)得 A([G]φ)，其中所有 pi都不在 A 和 φ 中出现。

·RG2′′：由 A([∧i∈GKiαi]φ)得 A([G]φ)，其中所有 αi都是 PL 公式。

有穷规则RG2与RG2′具有同等的推演能力，这可以采用类似于[1,Lemma 17]的证明得到。另一方面，有穷规则RG2′不比无穷规则RG2′′弱：满足RG2′′的前提则也满足RG2′的前提。

由此首先可以得到GSAL和GSAL′是证明能力相同的系统：这两个系统的定理集完全一致。GSAL′′的证明能力则不强于GSAL′，即前者的定理集是后者定理集的子集。在第6.4节给出完全性结论后，事实上知道GSAL′′的证明能力并不弱于GSAL′。因此结论是，这三个系统的证明能力相同。

所有GSAL的定理都是有效的，是为系统GSAL的可靠性（soundness）。要证明这个结论，只需要证明相应公理系统的所有公理都有效，并且所有规则都可靠（即保持有效性）即可。就GSAL而言，PAL公理的有效性和规则的可靠性已知，此外不难证明规则AG和RG1的可靠性。需要证明的主要是规则RG2的可靠性。与之等价地可以证明RG2′的可靠性，并由此知规则RG2′′的可靠性。接下来给出证明RG2′的可靠性证明。

首先定义GSAL公式的复杂度，这样做是为了使公式[G]φ的复杂度高于φ和群体宣告的内容∧i∈GKiαi，从而实现归纳证明。

定义6.1(公式复杂度) 公式φ的复杂度c(φ)由如下条件归纳得到：ψ，考虑两个对其进行代入后得到的公式：ψα表示而ψ−α表示则对任意模型M，存在模型M′，使得：

(1) 对任意 i∈ {1,...,k}，〚qi〛M′= 〚αi〛M′= 〚αi〛M；

(2) 对任意GSAL 公式 φ，〚φ〛M′= 〚φα〛M。

其中，对任意公式 φ和模型 M，〚φ〛M表示 φ在 M 中的真值集，即 〚φ〛M={s|M,s|= φ}（下同）。

证明:类似于[1,Lemma 8]的证明。 □

引理4任给群体G={1,...,n}，GSAL公式ψ和不在ψ中出现的一组命题变元 p1,...,pn。如果知识状态 (M,s)使得（其中对任意i∈G，αi是PL公式），则存在模型N使得：①②对ψ中出现的所有命题变元r都有〚r〛N=〚r〛M，且③对任意i∈G都有〚pi〛N=〚αi〛M。

证明:假设引理的前提成立。令P={p1,...,pn,...}为一集命题变元，使得其中每个元素都不在ψ中出现。令Q={q1,...,qn,...}为一集新的命题变元，其中每个元素都不在P、ψ和任意αi（i∈G）中出现；公式即由引理3(2)知存在M′使得对所有pQ都有〚p〛M′=〚p〛M（引理3(2)中的“φα”在此时是pα，即p），且由引理3(1)知对所有i∈G有 〚qi〛M′= 〚αi〛M；再由假设和引理 3(2)知

将P视为引理3前提中的Q，将{q1,...,qn}视为{α1,...,αk}。对所有qP，由引理3(2)知存在N 使得，〚q〛N= 〚q〛M′（引理3(2)中的“φα”在此时是qα，即q），且由引理 3(1)知对所有 i∈ G，〚pi〛N= 〚qi〛M′。在引理3(2)中，将视为φ，则（因P∩Q=∅），即又因（上一段已证），有此外，对于ψ中出现的所有命题变元r，因为P、Q和ψ中出现的命题变元互不相交，有rP且rQ，根据前面的结论知〚r〛N=〚r〛M′=〚r〛M且对所有i∈G，〚pi〛N= 〚qi〛M′= 〚αi〛M。 □

引理5任给群体G={1,...,n}，容许型A，GSAL公式ξ和一组不在A([G]ξ)中出现的命题变元pi(i∈G)。如果存在知识状态(M,s)=((W,～,V),s)使得 M,sA([G]ξ)，则存在模型 M′=(W,～,V′)，使得 M′,sA([∧i∈GKipi]ξ)且对A([G]ξ)中出现的所有命题变元r都有V′(r)=V(r)。

证明:任给群体G，容许型A，GSAL公式ξ和一组不在A([G]ξ)中出现的命题变元pi(i∈G)。首先，对任意知识状态(M,s)，容许型A和GSAL公式ξ，如果M,s ̸A([G]ξ)，则存在 PL 公式集 {αi|i∈ G}，使得 M,s ̸A([∧i∈GKiαi]ξ)。通过施归纳于A的结构不难证明。

根据上述结论，要证本引理，证明如下结论足矣：对任意知识状态(M,s)=((W,～,V),s)，容许型 A 和给定的 ξ，如果 M,sA([∧i∈GKiαi]ξ)，则存在模型M′=(W,～,V′)使得：①M′,sA([∧i∈GKipi]ξ)，②对A(ξ)中出现的所有命题变元r都有V′(r)=V(r)，且③对任意i∈G都有V′(pi)=〚αi〛M。

施归纳于容许型A的结构：

(1)A=#：此时 A([∧i∈GKiαi]ξ)=[∧i∈GKiαi]ξ，可由引理 4 得到结论。

(2)A=KiA′：此时 A([∧i∈GKiαi]ξ) 为 KiA′([∧i∈GKiαi]ξ)。如果 M,s ̸KiA′([∧i∈GKiαi]ξ)，则存在 t～is 使得 M,tA′([∧i∈GKiαi]ξ)。根据归纳假设，存在 M′=(W,～,V′)使得 M′,tA′([∧i∈GKipi]ξ)，对 A′(ξ)中（即 KiA′(ξ)中）出现的所有命题变元r都有V′(r)=V(r)，且对任意i∈G都有V′(pi)=〚αi〛M。此时有 M′,sKiA′([∧i∈GKipi]ξ)。

(3)A=[φ]A′：此时 A([∧i∈GKiαi]ξ) 为 [φ]A′([∧i∈GKiαi]ξ)。如果 M,s[φ]A′([∧i∈GKiαi]ξ)，则 M,s|= φ 且 M|φ,sA′([∧i∈GKiαi]ξ)。根据归纳假设，存在与M|φ仅赋值上有区别的模型(M|φ)′=(W|φ,～|φ,(V|φ)′)使得：①(M|φ)′,sA′([∧i∈GKipi]ξ)，②对A′(ξ)中出现的所有命题变元r都有(V|φ)′(r)=(V|φ)(r)，且③对任意i∈G都有(V|φ)′(pi)=〚αi〛M|φ。定义模型M′=(W,～,V′)使得：

·对所有在 [φ]A′(ξ)中出现的命题变元 p，V′(p)=V(p)；

·对所有 i∈ G，V′(pi)= 〚αi〛M；

·对所有其它命题变元 q，V′(q)=(V|φ)′(q)。不难验证：

·〚φ〛M′= 〚φ〛M，M′,s|= φ，且 M′|φ =(M|φ)′；所以有 M′|φ,sA′([∧i∈GKipi]ξ)，并因此 M′,s[φ]A′([∧i∈GKipi]ξ)；

·对所有在[φ]A′(ξ)中出现的命题变元r，V′(r)=V(r)（由定义给定）；

·对所有 i∈ G，V′(pi)= 〚αi〛M（由定义给定）。

(4)A=(φ → A′)：此时 A([∧i∈GKiαi]ξ) 为 φ → A′([∧i∈GKiαi]ξ)。对任意知识状态 (M,s)=((W,～,V),s)，如果 M,sφ → A′([∧i∈GKiαi]ξ)，则M,s|= φ 且 M,sA′([∧i∈GKiαi]ξ)。根据归纳假设，存在模型M′=(W,～,V′)使得：①M′,sA′([∧i∈GKipi]ξ)，②对A′(ξ)中出现的所有命题变元r都有V′(r)=V(r)，且③对任意i∈G都有V′(pi)=〚αi〛M。

然而模型M′未必能够使得M′,s|=φ。为此定义模型M′′=(W,～,V′′)，其中对所有在φ中出现的命题变元p，都有V′′(p)=V(p)；对其余命题变元q，有V′′(q)=V′(q)。不难验证 A′([∧i∈GKipi]ξ在 M′和 M′′中的所有状态上同真同假（根据定义pi(i∈ G)不在φ中出现，因此V′′(pi)=V′(pi)；而A′(ξ)中出现的所有任意变元r，如果r在φ中出现则V′′(r)=V(r)=V′(r)，如果不在φ中出现则仍有 V′′(r)=V′(r)），因此 M′′,s ̸A′([∧i∈GKipi]ξ。

对{pi|i∈G}不在其中出现的任意公式ψ，定义模型N=(W,～,U)使得：

·对所有在ψ中出现的命题变元p，都有U(p)=V(p)；且

·对所有其它命题变元q，有U(q)=V′(q)。

下面证明结论：对M和N的所有具有相同个体域的子模型Ms和Ns，对任意状态w和任意公式ψ使得{pi|i∈G}不在其中出现，Ms,w|=ψ当且仅当Ns,w|=ψ。由此可得M′′,s|=φ。施归纳于c(ψ)：基本情形和命题联结词情形易证，下面证明模态词的情形。

·Kiχ情形：Ms,s|=Kiχ，当且仅当对所有t∈ Ms，如果s～it则Ms,t|= χ，当且仅当对所有t∈Ns，如果s～it则Ns,t|=χ（归纳假设）,当且仅当Ns,s|=Kiχ。

·[ψ1]ψ2情形：Ms,s|=[ψ1]ψ2，当且仅当如果 Ms,s|= ψ1则 Ms|ψ1,s|= ψ2，当且仅当如果Ns,s|=ψ1则Ns|ψ1,s|=ψ2（Ms|ψ1和Ns|ψ1有相同个体域），当且仅当 Ns,s|=[ψ1]ψ2。

·[G]χ情形：Ns,s ̸|=[G]χ，当且仅当存在PL公式集{βi|i∈ G}使得Ns,s|=使得（由 N 的定义和 ③ 知 U(pi)=V′(pi)= 〚αi〛M，故由归纳假设当且仅当

由上述结论知：M′′,s|=φ，因此如下结论都成立：

·M′′,sφ → A′([∧i∈GKipi]ξ)；

·对φ→A′(ξ)中出现的所有命题变元r都有V′′(r)=V(r)（根据定义，对φ中出现的所有命题变元p，V′′(p)=V(p)；而A′(ξ)中出现的所有任意变元r，如果r在φ中出现则V′′(r)=V(r)=V′(r)，如果不在φ中出现则仍有V′′(r)=V′(r)）；

·对任意i∈G都有V′′(pi)=〚αi〛M（因为pi不在φ中出现，所以由V′′定义和 ③ 知 V′′(pi)=V′(pi)= 〚αi〛M）。

因此，M′′是满足条件的模型。

(1)–(4)完成了对容许型的归纳，证明完毕。 □

上述引理与[1,Lemma 16]非常相似，但那里是针对GAL的证明，其中的错误在于归纳步骤A=(φ→A′)无法得到。上述引理中针对GSAL则该步可以通过。

引理6规则RG2′在GSAL中保持有效性。

证明:假设RG2′不保持有效性。则存在容许型A使得A([∧i∈GKipi]φ)有效且A([G]φ)不有效。因此存在知识状态不满足A([G]φ)。由引理5知存在知识状态不满足 A([∧i∈GKipi]φ)，与假设矛盾。 □

定理8 GSAL、GSAL′和GSAL′′都是可靠的。

6.4 完全性

本节主要证明系统GSAL′′的完全性定理，由此可以得到GSAL的完全性（GSAL是比GSAL′′证明能力更强的系统）。GSAL′′完全性定理的证明使用常见的典范模型方法（canonical model method），证明过程类似于[2,第4节]。4除了逻辑和公理系统的差别，本文与参考文献中的不同还在于对极大一致理论的定义不同[2,第4节]中使用的极大一致理论定义不同于常见定义，本文重新用回常见定义以便于阅读，证明过程并未复杂化），并且本文证明强完全性定理而非弱完全性定理。

任给公式集Φ和公式φ，称Φ推出φ（记为Φ⊢φ），如果存在Φ的有穷子集Ψ使得以Ψ为前提集可构造以φ结束的GSAL′′证明序列。称Φ一致（consistent），如果ΦGSAL′′⊥。称Φ极大一致（maximal consistent），如果Φ一致且真包含Φ的任何公式集都不一致。极大一致的公式集也被称为极大一致理论，简称理论。

理论的上述定义与经典定义并无二致，具有对命题联结词的一些封闭性质，这里不再赘述。Lindenbaum引理同样成立，即任何公式集都可以扩充为理论，证明从略。

定义6.2(典范模型) Mc=(Wc,～c,Vc)称为典范模型（canonical model），如果：

·Wc是所有理论的集合；

·～c∶ag→ ℘(W ×W)使得当且仅当{φ|Kiφ ∈ x}={φ|Kiφ ∈y}；

·Vc∶pr→ ℘(W)：x∈ Vc(p)当且仅当p∈x。

定义6.3(按序宣告) 任给有穷公式序列〉和理论Φ。称Φ对按序宣告封闭，当且仅当 ψ1∈ Φ，[ψ1]ψ2∈ Φ，……且 [ψ1]···[ψk−1]ψk∈ Φ。

上述定义将有助于接下来对真值引理的叙述和证明。

引理7(真值引理) 令φ为一公式。对于所有的理论x和所有有穷公式序列如果 x 对按序宣告封闭，则 Mc|ψ1|···|ψk,x|= φ 当且仅当[ψ1]···[ψk]φ ∈ x。

证明:施归纳于c(φ)：

基本情形：结论对所有PL公式成立。证明较简单，此处略去。

Kiχ 情形。从右至左：证明其逆否命题；令 Mc|ψ1|···|ψk,xKiχ，由语义定义，存在理论 y 使得：且 Mc|ψ1|···|ψk,yχ——其中 ～′是模型Mc|ψ1|···|ψk三元组的第二个元素——故有(Mc,y)满足按序宣告，再反复使用归纳假设可得y对按序宣告封闭。因而由归纳假设可得[ψ1]···[ψk]χy。由x～iy知{φ|Kiφ∈x}={φ|Kiφ∈y}，因此[ψ1]···[ψk]χx，故而Ki[ψ1]···[ψk]χx。由公理AK可得[ψ1]···[ψk]Kiχx。从左至右：证明其逆否命题；假设[ψ1]···[ψk]Kiχx，由引理前提和定理6可得Ki[ψ1]···[ψk]χx。令y={φ |Kiφ ∈ x}∪{¬[ψ1]···[ψk]χ}。y 一致（假设不一致，则存在 φ1,...,φn∈{φ |Kiφ ∈ x} 使得 ⊢ (φ1∧···∧φn)→ [ψ1]···[ψk]χ，因此⊢ (Kiφ1∧···∧Kiφn)→Ki[ψ1]···[ψk]χ，并进一步有 Ki[ψ1]···[ψk]χ ∈ x，与假设矛盾）。将 y 扩充为理论y′，则{φ|Kiφ∈x}⊆y′且[ψ1]···[ψk]χy′。因此且y′对于按序宣告封闭。由归纳假设，Mc|ψ1|···|ψk,y′̸χ。因此 Mc|ψ1|···|ψk,x ̸Kiχ。

[χ]ξ情形：假设 Mc|ψ1|···|ψk,x[χ]ξ，则 Mc|ψ1|···|ψk,x|= χ 且 Mc|ψ1|···|ψk|χ,xξ。由合取支前者、归纳假设和引理的按序宣告封闭条件知 [ψ1]···[ψk]χ∈x，由此再根据归纳假设和引理条件可得[ψ1]···[ψk][χ]ξx。反过来，假设[ψ1]···[ψk][χ]ξx，则 ¬[ψ1]···[ψk][χ]ξ∈x，则〈ψ1〉···〈ψk〉〈χ〉¬ξ∈x，根据定理 7，有 [ψ1]···[ψk]χ ∈ x。因此 x 对 〈φ1,...,φk,χ〉按序宣告封闭，由归纳假设，Mc|ψ1|···|ψk|χ,xξ。因此，Mc|ψ1|···|ψk,x[χ]ξ。

[G]χ 情形：假设 Mc|ψ1|···|ψk,x[G]φ，则存在 PL 公式序列 {αi|i ∈G}，使得 Mc|ψ1|···|ψk,x[∧i∈GKiαi]φ，则 Mc|ψ1|···|ψk,x|= ∧i∈GKiαi且Mc|ψ1|···|ψk|∧i∈GKiαi,xφ。根据归纳假设，[ψ1]···[ψk]∧i∈GKiαi∈ x，并因此 x 对 〈ψ1,...,ψk,∧i∈GKiαi〉按序宣告封闭。使用归纳假设可得 [ψ1]···[ψk][∧i∈GKiαi]φx。由公理[G]φ→[∧i∈GKiαi]φ 和宣告规则RA，可得[ψ1]···[ψk][G]φx。

反过来，假设[ψ1]···[ψk][G]φx，根据规则RG2′′和理论的定义可知，[ψ1]···（其中所有 αi都是PL公式）。由理论的性质知¬[ψ1]···[ψk]因此由定理7 知 [ψ1]···[ψk]前者结合引理中的按序宣告封闭条件可得 x 对按序宣告封闭；后者结合公理 ([φ]¬ψ ↔(φ → ¬[φ]ψ))和理论的性质可得根据归纳假设，因此，Mc|ψ1|···|ψk,x[G]φ。□

定理9(强完全性) 任给公式集Φ，如果在GSAL′′中Φ一致，则Φ可满足。（这等价于：任给公式集Ψ和公式φ，如果Ψ|=φ则Ψ⊢GSAL′′φ。）

证明:首先使用Lindenbaum引理将Φ扩充为理论Φ+。由真值引理知Mc,Φ+|=φ当且仅当φ∈Φ+。因此Mc,Φ+|=Φ，即Φ可满足。 □

7 结论

本文探讨了一种特殊的群体宣告逻辑：仅允许群体宣告一阶知识，这一设定适用于很多实际场合；文中称这类逻辑为群体简单宣告逻辑。群体简单宣告逻辑与公开宣告逻辑（[13]）、任意公开宣告逻辑（[2]）、群体宣告逻辑（[1]）等一脉相承，在逻辑性质和证明方法等方面与群体宣告逻辑颇为相似，但也有很多不同之处；突出的例子如，对后者不可靠的有穷规则对前者可靠，后者的有效式〈G〉〈H〉φ→〈G∪H〉φ（“多群依次宣告可由一次宣告实现”）不是前者的有效式。文章对群体简单宣告逻辑进行了细致的探索，包括逻辑有效式、表达能力、公理系统及其完全性证明等，也附带着对群体宣告逻辑进行了梳理。

我们尝试将群体简单宣告逻辑的表达能力与群体宣告逻辑进行对比，但尚未得到结论，因此在第5节中避而不谈，只能将这一开放性问题留待今后解决。在群体（简单）宣告逻辑（以及任意公开宣告逻辑）中添加公共知识和分布式知识等群体知识算子是下一步工作的主要目标之一，比如群体宣告与群体知识如何形成互动就是一个有意思的问题。计算复杂性问题也同样值得探索。在群体宣告中允许事实改变或非公开宣告等想法都是一直被提及却从未被解决的问题。我们将在今后逐步探索下去，但这些都超出了本文所能涵盖的范围。

[1]T.Ågotnes,P.Balbiani,H.van Ditmarsh and P.Seban,2010,“Group announcement logic”,Journal of Applied Logic,8(1):62–81.

[2]P.Balbiani,A.Baltag,H.van Ditmarsh,A.Herzig,T.Hoshi and T.de Lima,2008,“‘Knowable’as ‘known after an announcement’”,Review of Symbolic Logic,1(3):305–334.

[3]P.Balbiani,2015,“PuttingrightthewordingandtheproofofthetruthlemmaforAPAL”,Journal of Applied Non-Classical Logics,25(1):2–19.

[4]P.Balbiani and H.P.van Ditmarsch,2015,“A simple proof of the completeness of APAL”,Studies in Logic,8(1):65–78.

[5]H.van Ditmarsh,W.van der Hoek and B.Kooi,2007,Dynamic Epistemic Logic,Netherlands:Springer.

[6]R.Fagin,J.Y.Halpern,Y.Moses and M.Y.Vardi,1995,Reasoning about Knowledge,Cambridge,MA:The MIT Press.

[7]R.Goldblatt,1982,Axiomatising the Logic of Computer Programming,Berlin:Springer-Verlag.

[8]J.Hintikka,1962,Knowledge and Belief:An Introduction to the Logic of Two Notions,Ithaca,New York:Cornell University Press.

[9]B.Kooi and J.van Benthem,2004,“Reduction axioms for epistemic actions”,Proc.Advances in Modal Logic,pp.197–211.

[10]B.Kooi,2007,“Expressivity and completeness for public update logics via reduction axioms”,Journal of Applied Non-Classical Logics,17(2):231–253.

[11]L.B.Kuijer,Unsoundness of R(□),http://personal.us.es/hvd/errors.html.

[12]J.-J.C.Meyer and W.van der Hoek,1995,Epistemic Logic for AI and Computer Science,New York:Cambridge University Press.

[13]J.A.Plaza,1989,“Logics of public communications”,in M.L.Emrich,M.S.Pfeifer,M.Hadzikadic and Z.W.Ras(eds.),Proceedings of the 4th International Symposium on Methodologies for Intelligent Systems(ISMIS ’89),pp.201–216.