探讨高中物理动态平衡问题的审题和解题技巧

凌旭

【摘 要】 力学知识一直以来都是高中物理知识中的重难点，其中动态平衡尤其令同学们头疼。近几年动态平衡的题目在高考物理卷中出现的越来越频繁，而且分值也呈现出不断上升的趋势。在文章中，我就以一个学生的视角出发，谈一谈我在解答动态平衡类问题经常用到的方法和思路，给同学们提供一些建议。

【关键词】 高中物理；动态平衡；解题技巧；建议

动态平衡是物体在受到多方力量的作用下，发生了平稳缓慢的唯一，在这个过程中物体始终保持一种平衡状态。这种题目的特点即物体总的受力合力为零，因此在阶梯过程中同学们的受力分析就直接决定了解题思路的正确与否。此外，物体平衡状态的隐含条件、矢量力的计算、力的合成分解等都给同学们解题设置了障碍。因此，在动态平衡问题的解题中，更需要注重技巧与方法的养成，才能起到事半功倍的效果。

一、动态图解法

动态度解法是基于物体受多个力的情况下，直接依据某一项力为参照，画出总体的受力分析图。这种受力分析方法的使用通常要确保物理所受力中有一个恒定不变的力，这样才能形成有效的参照；并且还需要有一个力只发生数值的变化，但是在矢量方向上却保持一致。同学们就可以依据题目中的已知信息，对物体进行受力分析图解，再根据常用的平行四边形分析法来判断某一项力的方向及大小变化。

比如在例题A中：物体受到金属线ab和ac的牵引，并悬挂在两面墙之间。在b点的上下平移而a位置不变的情况下，求b点向上移动ab和ac所受的拉力情况。

在这道题的解答中，我首先确定以悬挂的物体为受力分析图的中心，然后在分析牵引物体的ab、ac受力情况。在动态平衡中，物体受到一个始终垂直水平面且大小不变的重力，也同时受到了ac大小不一但方向恒定的拉力，以及ab方向和大小都在不断变化的拉力。由题目信息“a”点位置始终不变可知物体受到的合理为0，那么我就可以建立起对应的力的平行四边形，通过图形内的直观比较可知：ab上的拉力经过了由减小到变大的两个过程，而ac的拉力则始终在减小。

二、相似三角形

相似三角形也是动态平衡问题分析中常见的一种办法，这种方法在受力分析的基础之上结合了几何中的三角函数知识，利用一些三角形固有的性质给受力分析提供了新的思路。当物理同时受到3个作用力时，其中有一个恒定不变的力，而另外两个力则大小方向均不断变化。这种题型利用普通的动态度解法就会遭遇困境，这时候就需要利用到相似三角形知识进行分析。

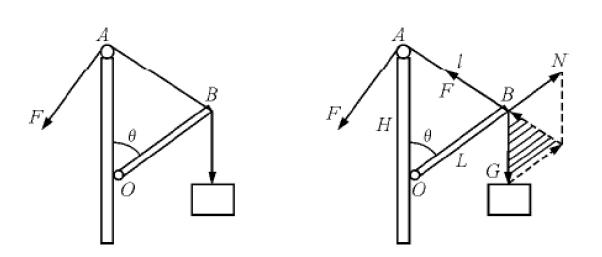
在例题B中：一物体通过细绳悬挂并紧贴墙面，此时利用一根金属棒OB支撑在墙面与细绳之间，并缓慢的向上拉动细绳，问在这过程中细绳的拉力与金属棒所受压力的变化情况（如下图）。

通过对题目的分析我发现，在平面内绳上的拉力、物体所受的重力与金属棒的压力恰似能构成一个三角形。而且金属棒的B端始终保持着一种动态平衡。于是我通过相似三角形的原理将△OAB与三个矢量力建立起联系，通过对比可以得出：（如上图所示），在细绳牵引的过程中，G、H、L都没有变化，l慢慢减小，由此可知压力并没有变化，而拉力却在逐渐减小。

三、正交分解法

正交分解法也是在力学环境下对三角函数的巧妙运用，对于力的大小求解有着显著的作用。正交分解法依赖于直角三角形的构建，因此在物理受力分析中必须存在垂直力的情况。而且也必须满足某一项力始终恒定不变的原则，通过与其它力的矢量关系来联立三角函数式。这种方法实际上是在解题过程中自行挖掘了一部分已知条件，将原本复杂的解题过程进行了有效的简化。

例题C：一规则的物体在细绳牵引力的作用下匀速前进，绳子与地面夹角为α，已知物体受到重力G，支撑力N，以及摩擦力和牵引力，当绳子长短发生变化时各力的变化情况。这道题目中涉及到3个以上的力，前文中所提及的解题方法在此处也均不适用，这时候就需要利用三角函数知识进行正交分解。

通过受力分析，我将物体所受的四个力在平面上画出来，并且利用绳子与地面夹角的关系得出方程式：Fsinα=f，N+Fcosα=G。由题目中物体匀速运动可以得出，该物体处于动态平衡的状态下，而且绳子长短的变化实际上反应为力的矢量变化即夹角α的变化。联立方程式可以得出，重力G拉力F不变的情况下，绳子变短则力N变小，力f也变小。

四、整体法和隔离法

在部分题目中物体受力系统可能存在多个部分，这时候我们就应该灵活地运用整体法与隔离法。一方面将大系统中平衡状态的条件进行总结，另一方面也通过对局部的分析方便对答案的求解。整体方法将物理问题中的对象作为整体来研究，隔离法则正好相反，將题目所求的部分从运动系统中剥离出来具体分析。

例题D：某物体通过细绳AB悬挂在水平直杆上，在细绳上有一点O施加拉力，在此过程中AB与直杆相连的A端始终保持原位置，求这个过程中杆与环的作用力，以及拉力的变化情况。

我先经过整体的分析方法，将细绳与物体视作同一个整体，对其进行受力分析，直杆与绳的作用力就能很清楚的呈现出来。然后由平衡条件可以得出，细绳与杆的作用力始终恒定。再使用隔离法对小球的重力以及O点的拉力进行分析，得出重力G始终不变而拉低随着夹角的变化逐渐变大。

【参考文献】

[1]王德立，彭七四，彭桐睿.力学中的动态平衡问题的探讨[J].湖南中学物理，2016（05）.

[2]董村生.高中物理动态平衡问题浅析[J].中学生数理化·物理篇，2016（06）：35-36.

[3]陈芹.高中物理中动态平衡问题的一般解析[J].数理化学习，2015（06）：31.