改进的小波域耦合偏微分方程图像去噪模型

王俊 杨成龙

摘要：针对全变分及四阶偏微分方程图像去噪模型的不足，利用小波变换能够聚焦到图像细微变化的优势，提出一种基于小波域的偏微分方程图像去噪算法。并通过对小波的阈值和阈值函数做适当的改进以及利用加权函数将全变分和四阶偏微分方程去噪模型相结合的方法，得到一种改进的小波域耦合偏微分方程图像去噪模型。MATLAB仿真结果表明，该模型和小波软阈值去噪、全变分模型以及四阶偏微分方程图像去噪模型相比，峰值信噪比有明显的提高，而且能够在很好地保留图像的边缘和细节信息的同时提高处理噪声的效率。

关键词：图像去噪;小波变换;偏微分方程;阈值函数;MATLAB

中图分类号：TN911.73

文献标志码：A

0 引言

图像在形成、获取和传输等过程中常常会受到噪声的干扰。噪声的存在不仅会影响图像的视觉效果，而且会对图像的后续处理工作带来一定困难，如图像压缩、边缘检测以及图像融合等等。因此，图像去噪是图像处理领域里的一个关键环节，具有非常重要的研究意义。

近十几年来，在图像去噪领域涌现出了两大发展主流[1]：一是基于小波分析的图像处理，小波分析具有良好的时频局部化性质，能把图像的纹理和结构信息表现在不同的分辨率层次上，在实现信噪分离的同时还能较好地保留图像的细节信息[2];二是基于偏微分方程（Partial Differential Equation，PDE）的图像处理，如P-M模型、全变分（TotalVariation，TV）模型[3]、四阶PDE模型[胡等等，它们在图像去噪方面都发挥了各种的优势，也取得了良好的去噪效果。但是小波去噪的缺点是模糊了图像的边缘，而且会产生一定的吉布斯和哑铃效应;TV模型在处理图像平坦区域时会产生“块状效应”，造成图像局部细节特征丢失的现象;四阶PDE模型去噪时容易使图像的光滑区域变得不平整。

针对以上问题，本文提出一种改进的小波域耦合二阶偏微分方程和四阶偏微分方程的图像去噪模型，该模型的去噪流程是：首先经小波变换对含噪图像进行阈值去噪，然后对图像的高频分量进行偏微分方程去噪，最后经小波重构得到去噪后的图像。本文模型克服了单独运用小波变换或二阶和四阶偏微分方程模型进行图像去噪的不足，能够在保持图像细节信息和边缘特征的同时，达到良好的去噪效果。

1 小波阈值去噪方法

小波阈值去噪的原理就是先对图像进行小波分解得到小波系数，把幅值较小的小波系数看作是噪声能量所提供，幅值较大的看作是图像本身能量所提供[5]，然后选择一个合适的阈值门限，规定比阈值门限低的小波系数当做噪声予以去除，达到去噪的目的。其去噪过程如图1所示：

其中，在进行小波系数阈值门限处理时，通常使用硬阈值处理方法或软阈值处理方法。

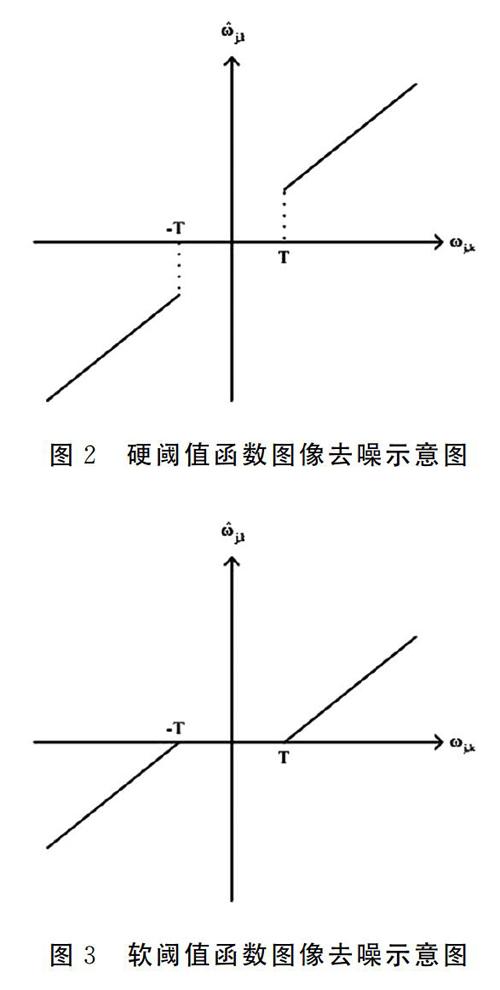
硬阈值是将图像的小波系数的绝对值和阈值门限进行比较，小于阈值门限的点小波系数置为O，其余的不变，设阈值门限为T，则硬阈值公式如下：

对应图像如图2所示：

软阈值与硬阈值不同之处是当图像小波系数大于或等于阈值门限时，小波系数值变为该点值与阈值的差，其公式如下：

2 偏微分方程去噪方法

图像总是存在突变的特征，鉴于此，1992年，Rudin，Osher和Fatime首次将全变分引入图像去噪领域，开创了全变分图像去噪方法，其模型表达式如下：

其中，u为观测到的图像，u0为原始图像，V为梯度算子。TV模型是一种各向异性扩散模型，扩散系数为1/ Vu，且只沿图像梯度垂直的方向进行扩散，水平方向不进行扩散，因此它能兼顾图像去噪和保护图像的边缘信息。但在图像平坦区域不一定存在边缘方向，此时若依然沿着边缘扩散，则会使去噪后的图像产生虚假边缘，产生“阶梯效应”，严重影响图像的视觉效果。

为了克服图像经二阶偏微分方程去噪后产生“阶梯效应”的现象，2000年，Y-L.You和M.Kveah提出利用高阶偏微分方程来处理图像，并给出了如下方程：

其中，c（|△2u|）是正的非增函数。四阶偏微分方程去噪模型是利用“分段斜面”来近似边界的，且方程中的拉普拉斯算子属于无方向性的微分算子，对噪声反应敏感，能够很好地消除“阶梯”效应。但在滤除平滑区域噪声时会造成“不平整”现象，且去噪效率低，往往需要大量的迭代才能获得较满意的去噪效果。

3 改进的小波域耦合偏微分方程图像去噪方法

3.1 改进的小波阈值函数和小波阈值

在小波阈值去噪时，大多采用硬阈值函数或软阈值函数其中的一种。硬阈值函数虽然能够较好地保留图像的边缘细节信息，但ωj，k在T和-T处不连续，利用ωj，k。重构后所得图像会出现视觉失真的效果[6]。软阈值函数去噪效果相对平滑，但这种算法减少了许多绝对值大的小波系数，对图像的高频部分造成了一定损失，最后导致图像变得模糊。为了克服硬、软阈值函数的上述缺陷，本文提出一种改进的阈值函数，其表达式如下：

其中，m>0，当m=0时，该表达式可以看作软阈值函数，当m一。。时可以看做为硬阈值函数。和硬阈值函数或软阈值函数相比，本文提出的阈值函数具有以下几个优点：①通过调整参数m的值，可以克服软阈值函数有偏差和硬阈值函数不连续的缺点，且具有能量自适应性。②该函数不仅和软阈值函数一样具有连续性，而且在ωj，k≥T处是高阶可导的，便于进行其他一些数学处理。③该函数以ωj，k=ωj，k为渐近线，ωj，k越大，ωj，k越接近ωj，k很好地克服了软阈值函数中ωj，k与ωj，k之间存在的恒定偏差。

在小波去噪中，阈值的选择非常关键，它对去噪效果的好坏起到了决定性作用：如果阈值太小，则去噪后图像任然含有较多的噪声，达不到去噪效果[7];如果阈值太大，则图像的许多有用部分会被去除，造成失真。目前，所使用的阈值包括全局阈值和局部阈值，且大多数去噪模型都采用了Donoho和Johnstone统一阈值，其表达式为δ=σ√2lnN。但是通常情况下，噪声会随着分解尺度的增加出现递减的趋势，若采用统一阈值将无法实现噪声的自适应变化，影响去噪效果。因此本文提出一種自适应阈值方法来克服统一阈值不随尺度变化的缺陷，其表达式如下：

但是这种阈值估计方法比较复杂，本文采用一种简单有效的阈值估计方法，即在图像进行小波分解的第一级，取小波系数中的HH部分，以它的标准方差σ的估计值σ1，再利用自适应阈值计算出阈值。

3.2 改进的偏微分方程去噪模型

为了充分发挥TV模型和四阶偏微分方程模型在图像去噪方面的优势，本文提出用一个加权函数将二者结合起来的偏微分方程去噪模型，新模型中将图像的能量函数取为：

权函数因满足以下要求[8]：

①在图像边缘區域，突出TV模型的作用，因此θ应接近1

②在图像平坦和渐变区域，突出四阶偏微分方程的作用，因此θ应接近0

综合以上两点，本文将权函数θ取为：

其中，M，N分别是图像的长和宽，I为原图像，J为处理后的图像，若峰值信噪比越大，说明去噪效果越好。

以大小为256×256像素的Lena图像为例，将本文模型与小波软阈值去噪方法、全变分模型、四阶PDE模型进行比较实验。其中，所加噪声为方差0.01的高斯噪声，迭代次数，n=50，空间步长h=1，时间步长△t=0.1，参数k=2。图5为几种模型的去噪效果对比图：

从图5可知，本文模型去噪效果明显优于TV模型、四阶PDE模型和小波阈值去噪方法，它不仅保留了小波去噪方法中很好保留图像细节信息的优势，而且还继承了TV模型和四阶PDE模型各自在图像去噪方面的优点，同时拥有较强的边缘保护和良好的保护图像平滑区域的能力。

图5各去噪模型对应的峰值信噪比如表1所示：

从表1可知，本文模型对应的峰值信噪比最大，说明去噪效果最好。

5 结论

通过分析小波变换和偏微分方程在图像去噪方面的特点，指出了两者的优点和不足，提出将小波阈值去噪和偏微分方程相结合的去噪思想，并对阈值和阈值函数做出相应的改进，以及利用一个权函数将TV模型和四阶偏微分方程相结合，最终得到一个改进的小波域耦合偏微分方程图像去噪模型，从MATLAB仿真实验结果看，本文模型既保护了图像的边缘纹理特征，又很好地保留了图像细节信息，同时还具有较高的峰值信噪比，所以本文模型是一个较好的图像去噪模型。

参考文献

[1] 王利娜，何文章，基于小波变换和ROF模型的图像去噪算法[J].天津职业技术师范大学学报，2015，25（5）：39-42.

[2]张文静，吴传生，刘欣.二阶TGV结合小波变换模的图像去噪算法[J].武汉理工大学学报，2015，37（1）：21-24.

[3]

RUDINL L，OSHER S，FATEMI E.Nonlinear totalvariation based noise removal algorithms [J]. Physisca D，1992，60（1/4）：98-109.

[4] YOU Yrli，KAVEH M. Fourth-Order partial differential e—quations for noise removal [J]. IEEE Transactions on ImageProcessing 2000，9 （10）：1721-1728.

[5] 曾诚，基于小波理论的图像去噪和增强技术研究[D].武汉：武汉理工大学，2008.

[6] 靳士利，基于小波变换的自适应图像去噪方法的研究[D].青岛：青岛大学，2010.

[7] 缪毅，基于小波变换与ROF模型的图像去噪方法研究[D].昆明：云南大学，2013.

[8] 张国伟，基于小波变换的图像去噪方法研究[D].昆明：昆明理工大学，2014.