永磁同步电机的分数阶建模方法

那景童 张旭秀

摘 要：将永磁同步电机（permanent magnet synchronous motor，PMSM）整数阶模型推广到分数阶，构造结构相同的分数阶电机模型。针对整数阶电机模型，基于遗传算法设计最优PID控制器，将所设计最优PID控制器作用于分数阶模型。通过调节分数阶模型分数阶次可得到電机调速系统的一簇阶跃响应曲线，选取该簇曲线中动静态特性相对最好的曲线所对应的分数阶次作为永磁同步电机的分数阶模型阶次，从而构造出永磁同步电机的分数阶模型。通过软件仿真和结果分析可得本文所构造的分数阶永磁同步电机模型具有更好的动静态特性和描述效果。

关键词：电机模型;分数阶模型;最优PID;调速系统;动静态特性中图分类号：TP203

文献标志码：A

0 引 言

永磁同步电机因其高可靠性、高效率和快速动态响应等诸多优点被广泛应用于机器人、医疗设备、汽车电子等领域[1-3]。在工业控制领域，大多数运动控制系统属于多惯量系统，有研究发现在多惯量系统的建模中，其模型适当的阶次往往不是整数，而是在两个临近的整数之[4，5]。同时研究表明，实际电容和电感具有分数阶特性[6]，既然像电容和电感这类储能元件属于分数阶的，那么包含电容、电感等储能元件的电机应该也属于分数阶的，因此采用分数阶微积分建立电机的数学模型能够更加细腻的刻画其动态行为，更为准确的描述其属性特征[7]。

随着对分数阶微积分的不断深入研究以及人们对于分数阶的认识和接受，开始逐渐意识到整数阶系统只是分数阶系统的一个特例[8]。因此，基于该从属关系可以得到一个事实，能够采用整数阶微积分描述的系统，分数阶微积分肯定能够描述，进一步研究发现，采用分数阶微积分描述的一些系统特性，用整数阶微积分来描述将会变得非常复杂或根本无法得到准确的整数阶系统模型[9，10]。所以，本文将永磁同步电机的整数模型推广到分数阶模型，具有理论意义和实际应用价值，是未来发展的趋势。

1 永磁同步电机数学模型

永磁同步电机的数学模型与普通同步电机的数学模型基本相同，其数学模型包括电机的电压方程、转矩方程和运动方程[11]，其具体建模过程可参考文献[11]。这里给出本文所采用的永磁同步电机等效电路如图1所示。

从图4和图5可以看出，将整数阶积分环节和整数阶惯性环节阶次推广到分数阶次可以加快系统的响应速度、使得系统的上升时间更快。那么在相同控制器作用下，分数阶模型应具有更好的控制效果。

2.3 永磁同步电机的分数阶阶次获取

2.3.1 分数阶阶次获取步骤说明

永磁同步电机分数阶模型的分数阶次ζ和θ选取步骤如下：

①保持最优PID控制器参数：Kp= 30.5145，

Ki=2 3.9175，Kd= 10.59值不变，采用永磁同步电机的分数阶模型即式（3）代替整数阶模型式（2），得到由PID控制器十分数阶模型组成的控制系统。

②在仿真平台，采用阶跃信号测试该控制系统，通过调节ζ和θ值，得到一簇PID控制器十分数阶模型的闭环速度单位阶跃响应曲线

③选取动静态特性相对最好的曲线所对应的ζ和θ值作为永磁同步电机的分数阶模型分数阶阶次。

由于永磁同步电机的整数阶模型阶次为2，1，分数阶模型阶次应该在整数阶模型附近[16]，才能不改变原电机模型的特性，那么本文将ζ和θ值得取值范围定为[0.65，1.45]和[0.7，1.5]，相应地分数阶模型的ζ+θ阶次取值范围为[1.35，2.95]，这样就将分数阶模型在原模型附近的阶次都囊括在内，表2给出了本文分数阶模型阶次的具体取值情况。

2.3.2 分数阶模型确定具体细节说明

如表2所示，这里列出25种ζ和θ值的组合情况，也就是说本文给出的永磁同步电机的分数阶模型有25个，确定分数阶模型的具体细节如下：

①将这25个分数阶模型按行分成5组，每组固定ζ值不变，通过五列θ对应的不同取值，即每组可产生5个分数阶模型。

②通过仿真绘制出每组最优器PID参数十分数阶模型的闭环阶跃响应曲线图，那么可以得到5幅PID控制器十分数阶模型的闭环阶跃响应曲线图，每幅图中包含5条曲线，选择每幅图中最优的一条曲线所对应的阶次作为永磁同步电机的分数阶模型，便可得到五个最优分数阶模型。

③最后将这五个分数阶模型进行对比，选择其中最优的一条作为最终永磁同步电机的分数阶模型。这里最优曲线的评判标准为：每条曲线的上升时间、超调、调节时间和ITAE（Integral Time Av-erage Error）值其数学表达式为：

式（7）中，e（t）为输入输出误差的绝对值;T为

控制系统输出信号跟踪上输入信号时间，ITAE作为评判标准之一涉及快速性、准确性、稳定性能够很好的评价控制系统的性能。

2.3.3 建立分数阶模型仿真实例

举例说明，下面图6给出了表2第三行，即第三组ζ=1.05时，通过每列对应0的不同取值，所得五条PID控制器十分数阶模型的闭环阶跃响应曲线：

由图6可得，曲线2对应的θ=0.9的ITAE值最小，同时考虑到上升时间、超调和调节时间相对较小符合系统控制要求，因此选取θ=0.9所对应的ζ和θ值作为永磁同步电机的分数阶模型阶次，即：

ζ = 1.05，θ=0.9。

按照同样方法选取其余4组最优ζ和θ值，具体选取过程在这里不再赘述，下面给出其余四组中最优ζ和θ值，分别为：

（0.65，1.3），（0.85，1.3），（1.25，0.9），（1.45，0.7）

将这5条曲线对应的ζ和θ值代入式（3）中得到如下5个永磁同步电机的分数阶模型，即：

图7绘制出了PID控制器十分数阶模型（式（8）一（12））的闭环阶跃响应曲线，其中G_f1- G_f5是五条最优分数阶模型。

为了进一步比较，表3列出了5条曲线的闭环速度单位阶跃响应性能比较。

通过表3可得，最优五组曲线中，曲线2所对应的ITAE值最小，此時曲线2对应的ζ=0.85、θ= 1.3，因此得到最终本文所选取的永磁同步电机的分数阶模型为：

2.4 最优的分数阶模型与整数阶模型比较

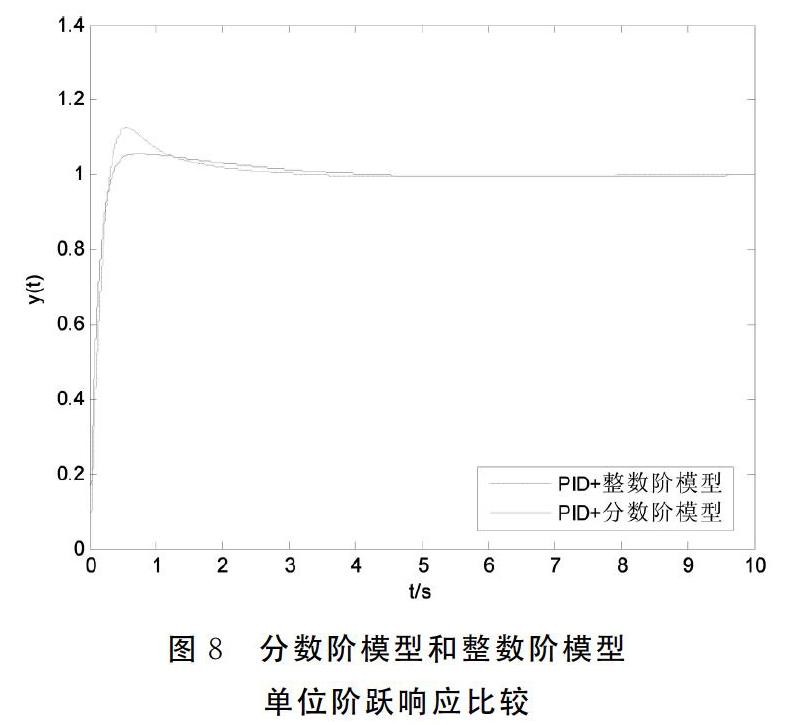
为了进一步验证本文所选永磁同步电机的分数阶模型存在意义，这里针对PID+电机分数阶模型（9）和PID+整数阶模型（2）进行闭环系统阶跃信号测试，如图8所示

从图8可看出，在同种控制器作用下，分数阶电机模型较传统整数阶模型，可提高整个控制系统的控制品质。

下面对本文所构造的分数阶永磁同步电机模型和原整数阶模型进行频域特性对比和分析，图9给出了式（3）和式（9）在控制器（5）作用下的开环频率特性曲线。

图9对比可看出，在同样控制器作用下分数阶电机模型与整数阶模型幅值特性无明显差异，而分数阶模型具有更大的稳定裕量。因此可得，本文所提的分数阶电机模型具有更好的频域特性。

3 结束语

给出了一种永磁同步电机的分数阶建模方法，将传统整数阶电机模型推广到分数阶次，基于整数阶电机模型设计控制器，在同种控制器作用下分别对整数阶电机模型和分数阶电机模型进行仿真研究。仿真结果表明，分数阶电机模型具有更好的控制性能，以及频域特性，从而证明所给方法的有效性。

参考文献

[1] 余伟.永磁同步电动机分数阶建模与研究[D].广州：华南理工大学，2014：13 - 14.

[2]赵佳奇，永磁同步发电机无速度传感器控制[J].控制工程，2016，23（11）：52-56.

[3]

BAIKI C，YOUN K K H，M J ROBUST. Nonlinear Speed Con-trol of PM Synchronous Motor Using Boundary Layer IntegralSliding Mode Control Technique [J]. IEEE Transactions onControl Systems Technology ，2000，8 （3）：47 -54.

[4] HUNGENAHALLY S. Neural basis for the design of frac-tional-order perceptual filters： Applications in image en-hancement and coding[C] IEEE International Conference，System，Man and Cybernetics 95 Intelligent Systems for the21st Century，1995，5：4626-4631.

[5] ORITIGUEIRA M D.Fractional Calculus for Scientists andEngineers[M]. New York： Springer Dordrecht Heidelberg，2011：228- 230.

[6] 王发强，马西奎.电感电流连续模式下Boost变换器的分数阶建模与仿真分析[J].物理学报，2011，60（7） ：45-46.

[7]赵远征.分数阶控制算法在永磁交流伺服系统中的研究与应用[D].南京：南京理工大学，2014.

[8]邓立为，宋申民，庞慧，控制系统的分数阶建模及分数阶PP Dμ控制器设计[J].电机与控制学报，2014，18（3） ：76-84.

[9] ELMAS C，USTUN 0.A hybrid controller for the speedcontrol of a permanent magnet synchronous motor drive[J].Control Engineering Practice，2008，16 （3）： 260- 270.

[10] 11 H S，LUO Y，CHEN Y Q.A Fractional Order Propor-tional and Derivative （FOPD） Motion Controller： TuningRule and Experiments[J]. IEEE Transactions on ControlSystems Technology，2010，18（2）：516- 520.

[11] 王瑞萍，皮佑国，基于分数阶控制器PMSM恒速控制[J].华南理工大学学报，2012.40（3） ：63-68.

[12]李刚，鱼佳欣，郭道通，等，基于改进遗传算法的机器人路径规划与仿真[J].计算技术与自动化，2015，6（2）：24-27.

[13] WANG Z B，CAO G Y，ZHU X J.Identification algorithmfor a kind of fractional order system [J].J of Southeast U-niversity，2004，20（3）：297-302.

[14]

MALTI R，AOUN M，SABATIER J，et al. Tutorial on sys-tem identification using fractional differentiation models[C]in：14th IFAC Symposium on System Identification， 2006，606 - 611.

[15] VICTOR S，MALTI R，MELCHIOR P，et al. Instrumentalvariable identification of hybrid fractional Box - Jenkinsmodels[C]//in： Proceedings of the 18th IFAC World Con-gress，2011，768-770.

[16]

GABANO J D，POINOT T. Fractional modelling and identifica-tion of thermal systems[J]. Signal Processing，2011，91（3）：531 -541.